矩阵结构遗传算法

潘 峰，龙福海，施启军，魏嘉银

(1.贵州民族大学 模式识别与智能系统省级重点实验室，贵州 贵阳 550025；2.华南理工大学 软件学院，广东 广州 510006)

0 引 言

遗传算法(Genetic Algorithm，GA)是由美国Michigan大学的John H. Holland教授与同事及学生等最先提出的一种随机自适应的全局搜索算法[1-2]。GA的数学框架及理论基础在20世纪70年代初期形成，Holland于1975年的专著《Adaptation in Natural and Artificial Systems》对这种理论进行了系统的论述。1989年美国伊利诺大学的David E. Goldberg的专著《Genetic Algorithms in Search，Optimization，and Machine Learning》对遗传算法理论及应用进行了比较全面的分析和例证[3]。Z. Michalewic于1992年的著作《Genetic Algorithms+Data Structures=Evolution Programs》对GA应用于最优化问题起到重要推动作用[4]。国内学者刘勇、康立山等[5]在1995年出版了《非数值并行计算(第2册)—遗传算法》，陈国良、王煦法等[6]在1996年出版了《遗传算法及其应用》，都对国内遗传算法的研究产生重要影响。

遗传算法为解决复杂优化问题提供了一种全新而有效的思路，其良好的全局搜索能力和健壮性得到众多学者的广泛认同；同时，其应用领域不断扩大，在机器学习[7-10]、软件测试[11-13]、图像处理[14]、神经网络[15]、工业优化控制[16-17]乃至社会科学[18]等领域均得到了成功的应用。GA主要包括选择、交叉、变异三种算子，算子在某种程度上决定着GA的应用性能，围绕三个算子的改进是最常见的研究方法[19-20]；另外，对算子改进的同时，采取的编码方式、设计恰当的适应度函数以及交叉率、变异率的调整都影响着GA的整体效能。

该文从系统科学角度出发，摒弃交叉率和变异率要素，着重于种群结构的改变，采用矩阵结构组织种群，在这种二维关系上构建算子。借助于矩阵的行、列及主对角线等概念组织子种群和描述改进算子，在保证计算性能的同时，简化演化程序的设计。并用面向对象的软件工程方法实现基于矩阵结构的遗传算法计算系统，以提升GA优化问题的效能。

1 矩阵结构遗传算法

1.1 测试问题描述与分析

任何算法的提出首先源于需要解决某个问题或者某类问题，而算法的改进也常常是源于问题领域扩展了或者需求更高了。该文主要是后者，即得到函数优化问题中更加精确的解。演化算法用于最优化问题是最为常见的应用，反之，用求解最优化问题的效果去验证算法改进的性能就成为首选工作。经典的最优化问题包括函数优化问题和组合优化问题，该文以函数优化问题为验证算法有效性的测试目标。不失一般性，函数求解最优解的形式为：

maximizef(x)

subject tox∈Ω

为便于对遗传算法进行描述，将优化问题设定为最大化问题。其中，x是决策向量，f(x)是目标函数，Ω是决策空间。

标准遗传算法采用二进制编码，用于函数优化问题效果并不理想，这使得人们逐渐转向粒子群优化算法、差分优化算法等。笔者认为，遗传算法是一种种群演化算法，具有系统特征，需要加强要素间的相互作用和构建良好的结构才能整体性地提升性能。为此，分析现在的许多演化算法特点，共性点是：构建的演化程序主要是采用一维线性结构，这种结构决定了算子设计也是比较简单的，从而最终的性能就比较有限。该文将从种群结构入手，构造二维关系的种群，简化选择算子和交叉算子，并提出克隆变异算子；选择算子实现了将各行最优个体构成父代集合，并置于矩阵的主对角线位置，父代集合中任何两个个体进行交叉产生两个子代，这里实际相当于以父代集合构建概率模型，而子代是完全符合概率模型分布的，这种完全交叉是一种特殊的分布式估计算法。另外，对变异算子引入克隆变异，使得变异朝着更好的方向进化，增强了竞争机制，以上算子的各种改进的最终目的是显著地提高遗传算法的整体性能。

1.2 基本遗传算法

标准遗传算法主要由选择算子、交叉算子以及变异算子构成。选择算子主要有轮盘赌选择、精英选择以及锦标赛选择等，其中轮盘赌选择是标准遗传算法常用的方法；它要求适应度值为正，在适应度值趋同的情形下优选效果不明显，所以需要设计适合的适应度值函数，这增加了计算工作量或设计的困难。精英选择法一般需要进行种群的排序处理，每次的迭代都进行排序操作增加了算法的计算复杂度。锦标赛选择法对于种群块的分组有一定难度，这种困难在于整个种群采用一维关系结构的原因。对于交叉算子而言，在种群规模为N的情况下，要进行N次交叉和N次选择操作，这是遗传算法计算性能不高的又一个原因。考察变异算子，虽然变异率取值一般不高，但变异效果可能是使基因退化。多种原因造成遗传算法计算效率低，不易全局收敛，对它的改进是很有必要的。

1.3 矩阵遗传算法

矩阵结构遗传算法是采用二维关系组织的种群演化算法，这种二维关系可以看作是由多个一维子种群构成，对于种群的分组变得简单。同样，这种二维关系赋予个体更多的属性，不仅有前驱和后继，还有属于哪个组的概念。显然矩阵结构种群中的每一个个体既可以属于行种群，也可以属于列种群，还可以视作某个块种群的个体。特别是拥有主对角线位置这个概念，将适合在设计算子时变得简单便捷，比如某些算子只作用在每个子种群，而不是对整个种群的操作，这对于工程化实现遗传算法系统很有价值。该文采用了行数和列数均相同的N×N方阵，方阵的主对角线上的N个精英个体进行完全交叉产生的N*(N-1)个子代个体刚好布置在方阵中除主对角线上的其他N*(N-1)个位置。

1.3.1 种群结构

文中种群结构采用二维关系，即是把种群划分为若干子种群，每个子种群规模一样大，如图1 所示，表示一个规模为25的种群结构，可以划分为5个行子种群或列子种群。在程序设计时，存储结构使用二维数组，数组的每一个元素为一个个体对象，代表问题的一个可能解。在每一行中，把该行最优适应度值个体首次出现的位置标记为灰色。在图1中为25个个体，第一行的a02标记为灰色，表示它是该行最优适度值个体。对每一行进行查找最优适度值个体，然后把它移动到主对角线位置，形成如图2所示的对角占优布局。

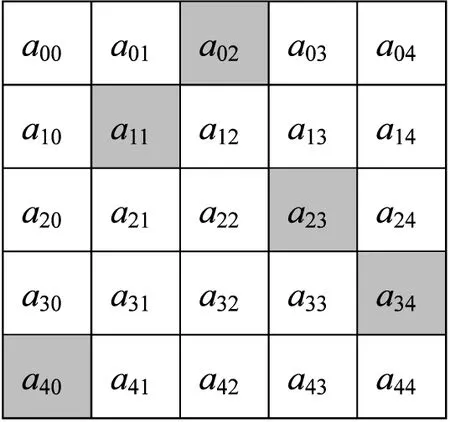
图1 初始矩阵结构种群

图2 对角占优的矩阵结构种群

根据图2所示，把行数相同的称为行种群，如{ai0,ai1,ai2,ai3,ai4}，列数相同的称为列种群，如{a0j,a1j,a2j,a3j,a4j}；行数与列数相同的称为主对角种群，如{a00,a11,a22,a33,a44}。明确种群结构及其划分，将在它的基础上定义各种算子。

1.3.2 行寻优与移动算子

对整个种群完成初始化操作后，第一步要做的就是挑选精英子种群，用来为产生下一代做准备。方法是对每一行查找该行最优适应度值个体的位置，然后把最优适应度值个体移动到该行的主对角线位置，即行数与列数相同的位置，处理结果如图2所示，{a00,a11,a22,a33,a44}即是精英子种群，将用来产生下一代。

1.3.3 精英完全交叉算子

交叉算子是选择精英子种群中个体进行两两交叉，每对父代产生两个子代个体，两个子代个体置放在关于主对角线对称的位置。用伪代码表示为：cross(a[i][i],a[j][j],a[i][j],a[j][i])，即是位于主对角线上的个体a[i][i]和a[j][j]进行交叉，生成的子代个体分别置于a[i][j]和a[j][i]位置。主对角线上的精英个体有n个，两两交叉产生n(n-1)个子代，刚好覆盖除主对角线上的n(n-1)个位置。

1.3.4 克隆变异

完成种群的交叉算子后，对矩阵结构种群的所有个体均进行克隆变异。其方法是：首先把当前要变异的个体基因复制到一个新创建的临时个体中，这个临时个体称为克隆个体，然后对克隆个体进行变异，若变异的克隆个体的适应度值优于当前个体，则将变异的克隆个体复制给当前个体，否则当前个体不变。经过逐一的克隆变异，将产生成熟的下一代。显然，整个种群经过克隆变异后，矩阵主对角线上的精英子种群比克隆变异前又进一步良性的进化。

1.3.5 算法描述

Step1：初始化矩阵结构种群P(t)，其中t为0，P(t)由P0,P1,…,PN-1共N个子种群构成，每个子种群的规模均为N，用A(i,j)表示N行N列矩阵结构种群P的第i行第j列元素；

Step2：逐行查找Pi中的最优元素Pi-best，并把它赋给A(i,i),i=0,1,…,N-1；

Step3：在主对角线位置种群{A(0,0),A(1,1),…,A(N-1,N-1)}中查找最优个体是否满足条件，若满足则输出，并结束；

Step4：让每对A(i,i)和A(j,j)元素进行交叉，产生的两个新个体分别赋给A(i,j)和A(j,i)，其中i≠j；

Step5：拷贝A(i,j)给临时个体Temp，对Temp实施变异，若变异的Temp适应度值优于A(i,j)元素，把Temp赋给A(i,j)，i=0,1,…,N-1,j=0,1,…,N-1；

Step6：t=t+1，跳转到Step2。

2 实验仿真与分析

2.1 实验环境

工作计算环境为多核CPU笔记本，其中硬件为：Intel Core i7-8750 CPU(六核12线程), 16 GB RAM；软件为Windows 10(64 bit)+JDK1.8，并使用NetBeans8.2集成开发环境。程序采用Java语言实现，未使用任何第三方软件包。

2.2 测试函数集

为验证矩阵结构遗传算法的性能，选择三个不同函数(见表1)进行求解最大值的实验测试，所列三个函数特征分别是：(1)单变量多极值；(2)二变量无穷极值；(3)多变量单极值。

表1 实验测试函数

2.3 实验结果

由于测试函数的变量维数不同，该文采用对每个函数测试的逐一比较。实验中对自变量的编码均采用二进制，鉴于二进制不适合于高维函数，因此测试选取较低维数函数或定义较小维数函数进行比较。

表2是标准遗传算法SGA与矩阵结构遗传算法MGA对f01函数求最大值的20次运行结果的处理数据，第一行为偏差，第二行为均值，第三行为20次运行中达到全局最优的次数。可以看出，SGA的种群规模越大效果越好，但递增程度减弱；在同等种群规模的SGA与MGA性能测试中，SGA单种群规模为400，MGA共20个子种群，每个种群规模为20，显然MGA性能远优于SGA。

表2 f01函数测试结果

表3是SGA与MGA对f02函数求最大值的20次测试结果。均采用了29位的二进制编码。在该函数测试中，从偏差和平均值结果看，种群规模对SGA影响性能不明显，无论哪种规模种群，SGA均未收敛到最优值；MGA的20次测试均收敛到最优值，优势明显。

表3 f02函数测试结果

表4主要比较了SGA与MGA算法在不同维数下求得的解与最优解之间的误差。f03函数是一个自变量维度可定义的函数，由于采用二进制编码，高维效果不好，该文只对1～9维的情况进行测试，表中分别给出与最优值的绝对值误差，若MGA性能优于SGA，则用+号表示,否则用-号表示。从表中很显然看出，随着自变量维数增加，SGA误差增加迅速，而MGA误差增加平缓，表现出很好的健壮性。

表4 f03函数测试的SGA与MGA误差对比

2.4 比较与分析

标准遗传算法与矩阵结构遗传算法的比较如表5所示。

表5 SGA与MGA的比较

从表5比较可以发现，SGA与MGA有许多不同之处：首先是存储结构的不同，SGA一般采用一维线性结构，而MGA采用二维矩阵结构，矩阵结构可以看作是对一维线性结构的分组，这种设计有利于仅仅是对组的操作而不需要对整个种群进行操作，比如对某行进行寻找最优个体的操作；其次是选择算子的设计简化了，只需要把每组的最优个体移动到主对角位置即可，全体主对角位置元素即是产生下一代的精英父代种群；最后是不使用交叉概率与变异概率这两个调试参数，交叉算子采用精英完全交叉，不需要交叉概率；同样，所有个体都进行克隆，对克隆个体进行变异，克隆变异强于原个体，则用克隆变异个体替换原个体，不使用变异概率。MGA一个最大的特点是位于主对角线上的精英种群是一种单调性递优演化的，即是下一代主对角线上的精英种群一定不弱于上一代精英种群。

图3～图5为标准遗传算法与矩阵结构遗传算法若干次迭代的收敛性比较，其中纵坐标为种群各代最优个体函数值与函数本身最优值的误差值，横坐标为迭代次数，虚线为SGA，实线为MGA；其中，f01、f02分别是一维、二维变量函数，f03是可变维数变量函数，为突出效果，选取的是8维变量，所有测试的种群规模均为64。在三个函数测试迭代次数的误差值图中明显看出，MGA均比SGA收敛速度快。由此可见，矩阵结构遗传算法MGA不仅计算精度优于标准遗传算法SGA，收敛速度尤其显著。

图3 f01函数收敛性

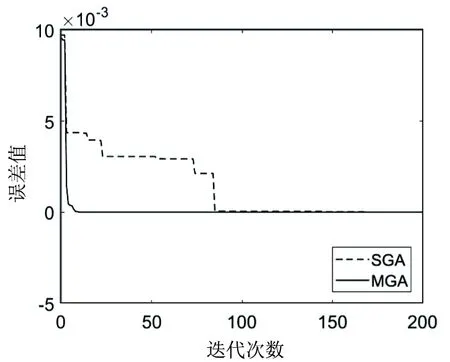
图4 f02函数收敛性

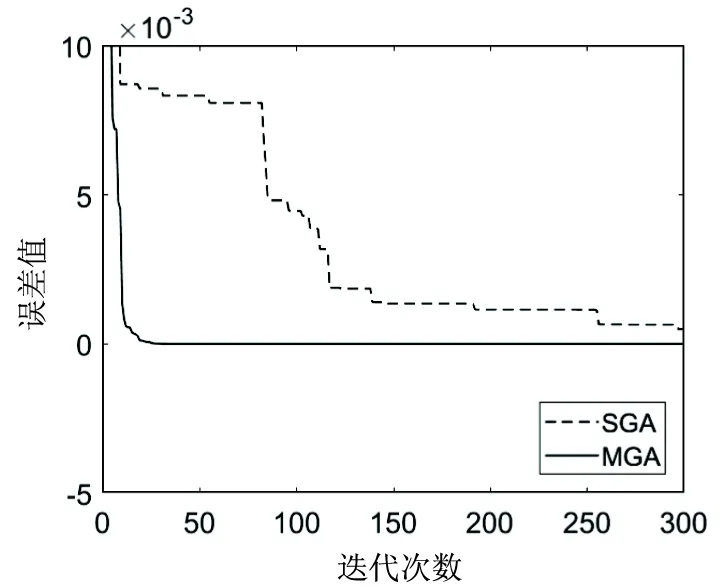
图5 f03函数收敛性

3 结束语

提出构建二维关系的种群，并在该结构上定义了新的演化算子，从而形成一种采用矩阵结构的改进遗传算法MGA。MGA设计的主要目的是提升算法的性能，使之在函数优化问题中更加健壮和适用。MGA通过对选择算子、交叉算子及变异算子的改进，性能及健壮性显著提高，与标准遗传算法在三个函数优化问题的测试比较，改进的遗传算法MGA性能优异。该改进的遗传算法还未对组合优化问题等其他优化问题进行测试，编码也仅仅采用了二进制编码，下一步工作计划将是采用浮点数编码进一步完善该算法。同时，基于矩阵结构进一步探讨如改进分布式估计算法、粒子群优化算法等演化算法也是下一步目标。