完备变分模态分解和多传感器卷积神经网络的轴承故障诊断方法

谭亚红，史耀

(重庆工程职业技术学院智能制造与交通学院，重庆 402260)

0 前言

滚动轴承被广泛应用于现代旋转机械中，很容易出现损伤而发生故障。因此，及时对旋转机械轴承进行故障诊断具有重要意义。

实际工业中传感器所测得的滚动轴承振动数据受噪声干扰较强，传统的基于机器学习的故障诊断方法存在较大缺陷。卷积神经网络(Convolution Neural Network，CNN)是深度学习的一种重要模型，它能从数据中自动学习相关特征，在一定程度上免去了繁琐的人工特征提取过程。宫文峰等为有效识别轴承微小故障，提出改进DCNNs-SVM方法，减少了CNN训练参数。曹继平等采用粒子群优化算法确定CNN结构和参数，故障识别精度高且鲁棒性好。但基于CNN的轴承故障诊断普遍存在以下缺陷：(1)CNN对多传感器振动信号的行、列方向同时卷积运算是不合理的；(2)振动信号中的噪声会降低CNN的特征提取能力与收敛速率。小波、EMD及其变体等降噪方法均存在一定的缺陷。变分模态分解(Variational Mode Decomposition，VMD)基于维纳滤波理论，具有坚实的数学理论基础，在故障诊断领域得到了一定应用。

本文作者在前述研究基础上，借鉴互补集合模态分解(Complementary Ensemble Empirical Mode Decomposition，CEEMD)的思想，对多个传感器测得的轴承振动数据进行CVMD分解并进行数据重建，将重建数据输入MSCNN进行轴承故障诊断。

1 CVMD降噪理论

1.1 VMD基础

轴承振动信号的变分模型如式(1)所示：

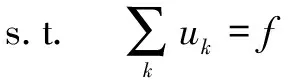
(1)

式中：{}为VMD的分解分量;{}为中心频率。式(1)的最优解由Lagrange算子求得：

({},{},{})=

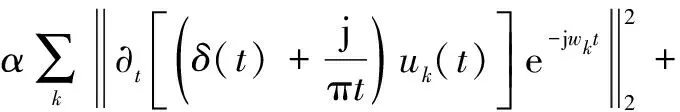
(2)

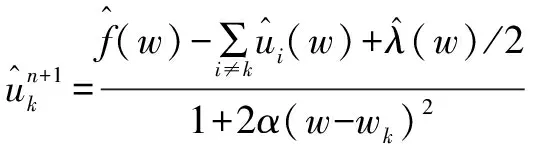
(3)

(4)

1.2 CVMD

为提高VMD分解结果的鲁棒性与稳定性，在轴承振动数据()中加入2对符号相反但幅值相等的白噪声，详细步骤如下：

(1)在轴承振动数据()中加入2对符号相反但幅值相等的白噪声()，由此得到1()和2()，如式(5)所示：

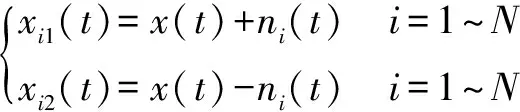
(5)

(2)利用VMD对1()和2()进行分解，如式(6)所示：

(6)

式中：IMF1,()和IMF2,()分别为1()和2()分解得到的IMF分量。

(3)重复步骤(1)和步骤(2)；

(4)循环次后，获得2××个IMF分量，然后进行平均化，如式(7)所示：

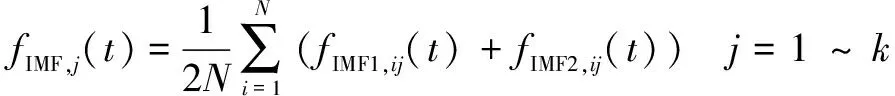
(7)

(5)进行数据重构，如式(8)所示：

(8)

1.3 综合指标

为保留轴承振动数据的故障特征信息，利用综合指标筛选有效的IMF分量。的表达式如式(9)所示：

=++0<、、<1

++=1

(9)

式中：表示IMF分量的峭度；表示IMF分量和原始数据间的相关系数；表示IMF分量的能量比，其中每个指标的权值均相同，并选择值最大的前4个模态分量进行重构。

2 MSCNN模型

传统的CNN模型对多个传感器测得的振动数据的行方向和列方向均进行卷积，但不同传感器所测得的数据是相互独立的，所以需要考虑不同传感器的不同组合。因此，本文作者提出一种MSCNN模型，如图1所示。

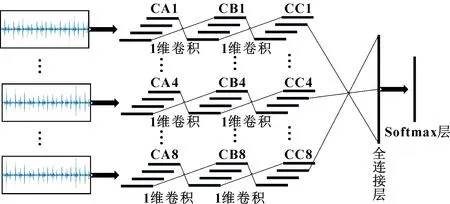
图1 MSCNN模型

图1所示的MSCNN模型中每个通道共有3个卷积单元、8个工业传感器，因此共有24个卷积单元，下面给出MSCNN的前向计算公式。

设输入=[，，…，]，(1≤≤8)为第个通道的振动信号，和分别代表卷积操作和池化操作，MSCNN输出如下：

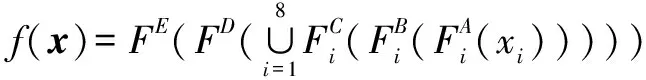
(10)

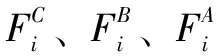
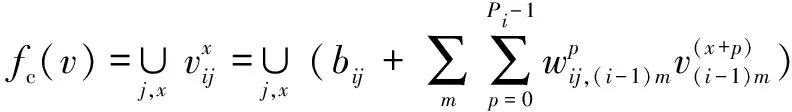
(11)

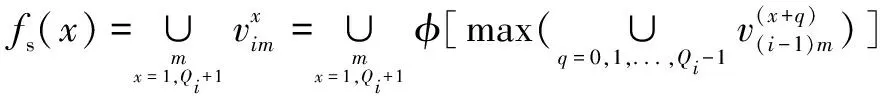
(12)

()=(+)

(13)

的表达式如式(14)：

(14)

函数的表达式如式(15)所示：

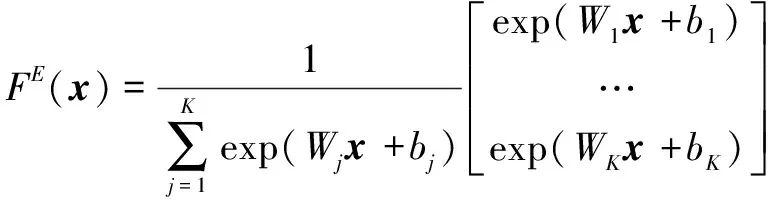
(15)

式中：为故障类别个数;和分别为权重和偏置。MSCNN采用和CNN相同的反向传播算法，详细步骤可参考文献[11]。

综上，基于CVMD-MSCNN的轴承故障诊断步骤如下，流程如图2所示。

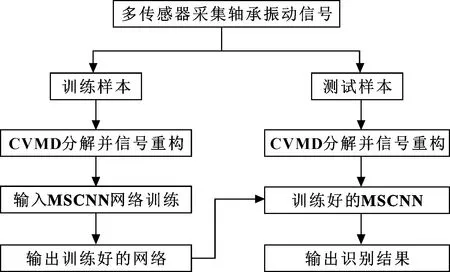
图2 CVMD-MSCNN故障诊断流程

(1)使用多个传感器采集轴承振动数据，并随机划分训练集和测试集；

(2)对训练集和测试集样本均进行CVMD降噪处理；

(3)将降噪的训练样本输入MSCNN进行训练；

(4)测试样本对MSCNN模型进行测试。

3 实验验证

3.1 实验数据描述

文中轴承实验台如图3所示，由电机、测试轴承、液压加载系统和加速度传感器等组成。采样频率设置为12 000 Hz，采用文献[12]所提方法进行样本分割，得到10种工况下的样本各12 000个，每个样本有2 048个采样点。轴承10种工况描述如表1所示。图4所示为滚动轴承10种运行工况的时域图。

图3 轴承实验台

表1 轴承10种工况

图4 轴承运行工况时域图

图5所示为图4所对应的包络谱图。由图4—图5可知信号受噪声干扰严重，难以对电机轴承的运行工况进行有效区分。

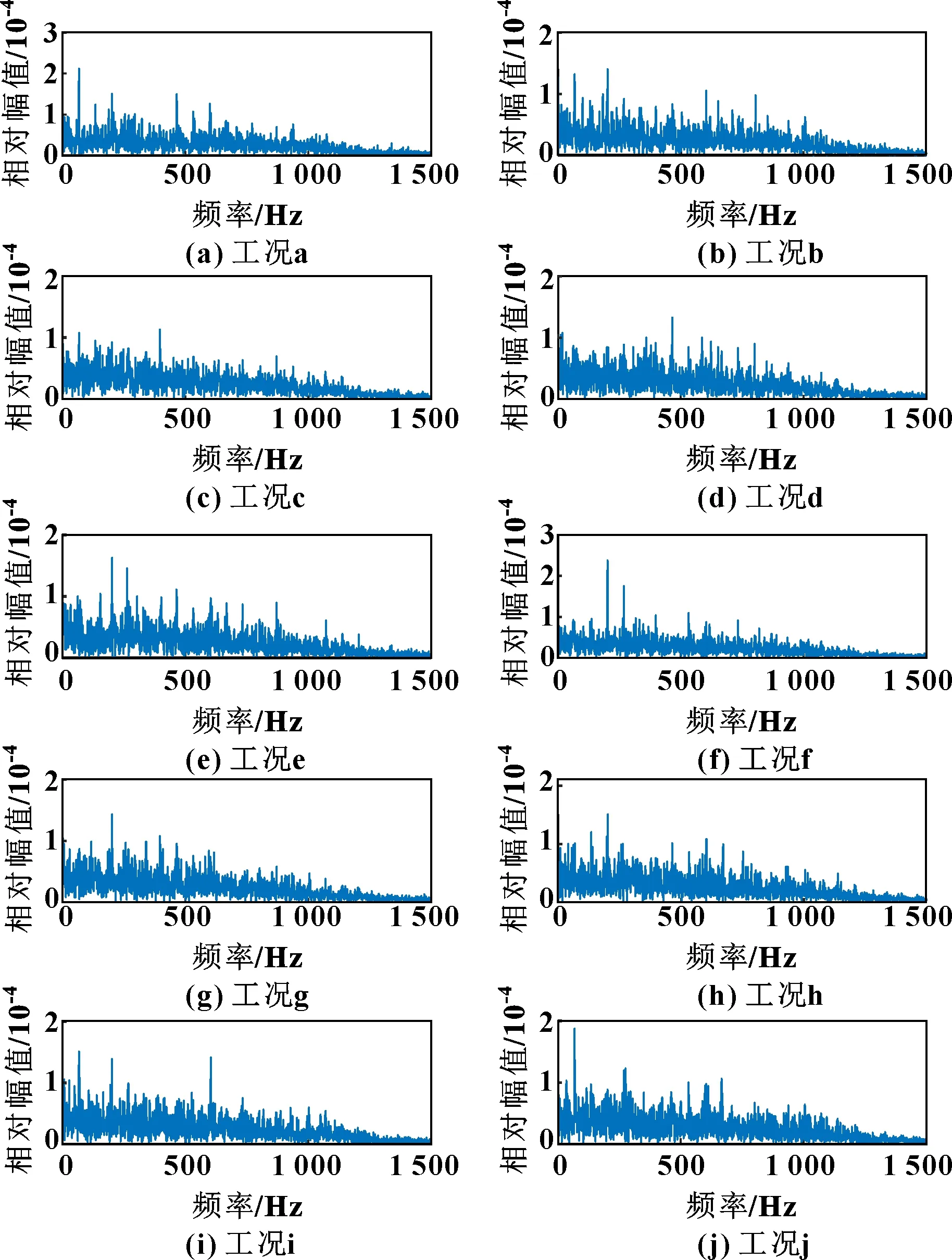
图5 轴承运行工况包络谱

3.2 信号分解对比

以工况g为例，分别采用CVMD和VMD进行信号分解，结果分别如图6—图7所示。

图6 工况g CVMD信号分解结果

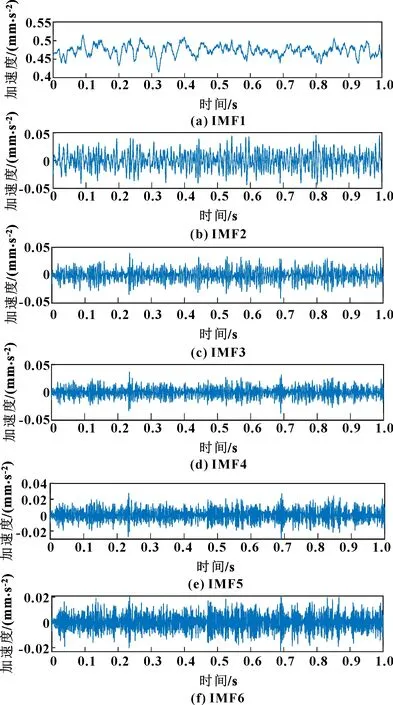
图7 工况g VMD信号分解结果

重建信号如图8所示。

图8 工况g信号重建结果

以均方根误差(Root Mean Square Error，RMSE)和信噪比(Signal to Noise Ratio，SNR)衡量降噪性能。VMD处理后信号的SNR和RMSE分别为3.12和0.787，CVMD处理后信号的SNR和RMSE分别为7.14和0.179，这表明CVMD相对于VMD更好地实现了重构降噪。

由式(16)计算得到轴承外圈故障特征频率约107 Hz。

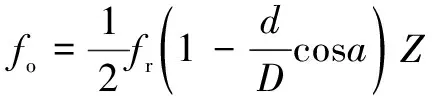
(16)

式中：为轴承滚子直径;为轴承节圆直径;为轴承接触角;为轴承滚子个数;为转频。

VMD、CVMD重建信号的时频谱图分别如图9、图10所示。可知：与VMD相比，CVMD重建得到的信号时频谱图时频谱脊线更明显，故障特征频率更清晰，进一步验证了CVMD的优越性。

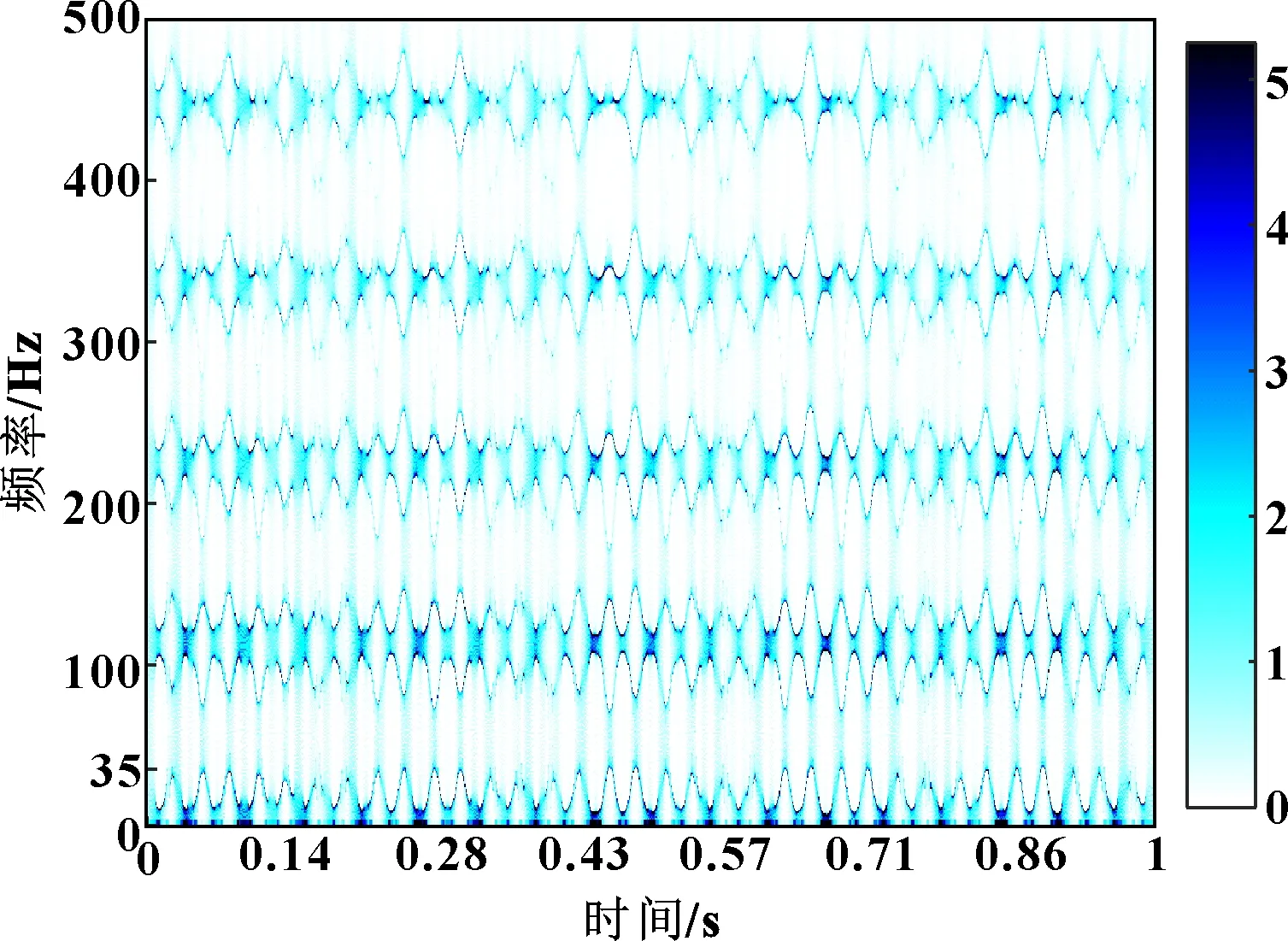
图9 VMD重建信号时频谱图

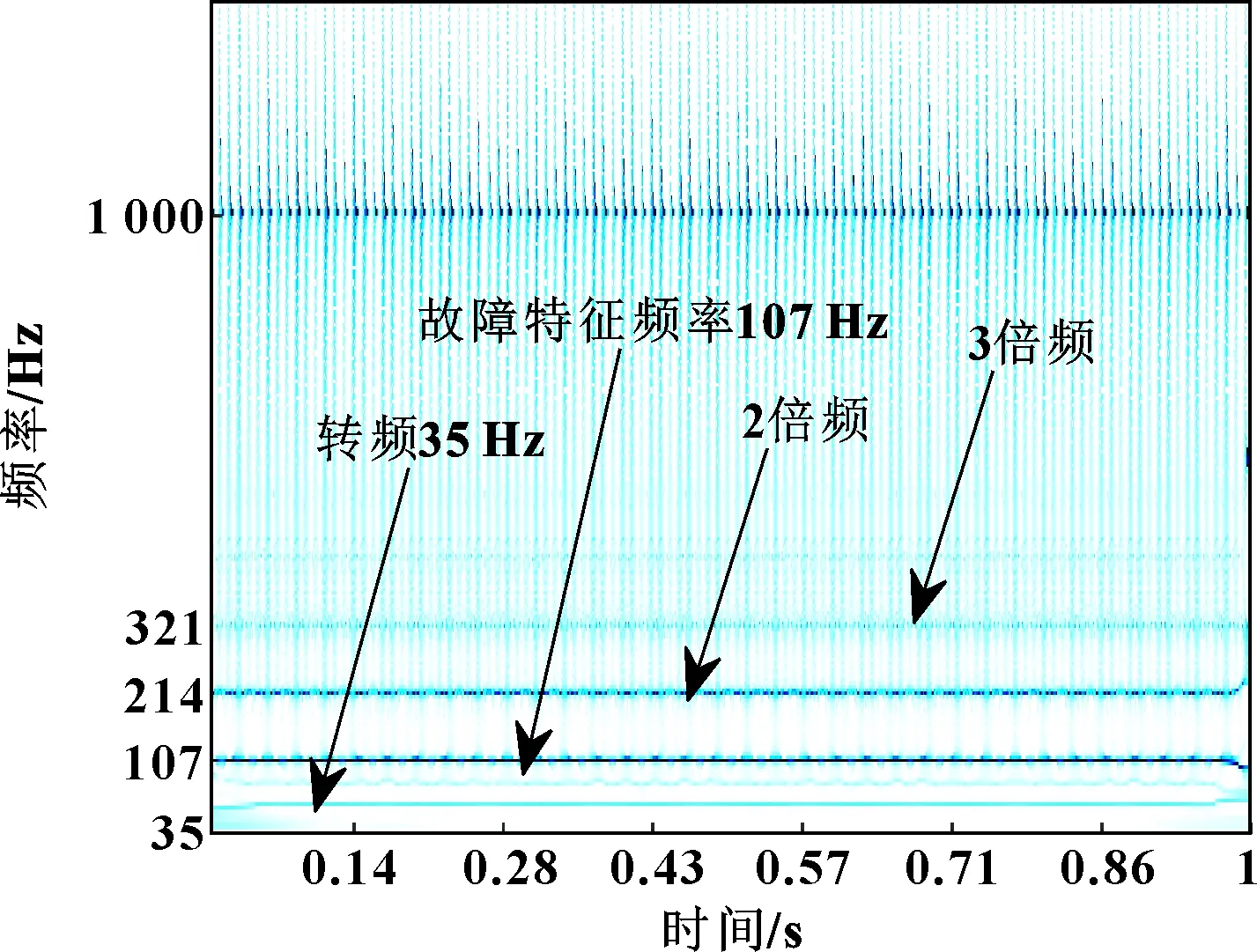
图10 CVMD重建信号时频谱图

3.3 故障诊断与对比分析

首先验证MSCNN的效果，采用文献[13]提出的多传感特征融合卷积神经网络(Multi-Sensor Signal Feature Fusion Using Deep Convolutional Neural Network，MSSFFDCNN)、文献[14]提出的改进残差网络(Improved Residual Network，IRN)和文献[15]提出的栈式自编码器(Stacked Auto-Encoders，SAE)进行对比分析。其中，方法1为CVMD-MSCNN；方法2为CVMD-MSSFFDCNN；方法3为CVMD-IRN；方法4为CVMD-SAE，方法5为信号直接输入MSCNN。表2列出了5种方法的平均诊断准确率。

表2 5种方法的平均诊断准确率

为验证CVMD的优越性，采用不同的降噪方法进行对比分析。其中，方法1为CVMD-MSCNN；方法2为VMD-MSCNN；方法3为CEEMD-MSCNN；方法4为EMD-MSCNN。表3列出了不同降噪方法的平均准确率。

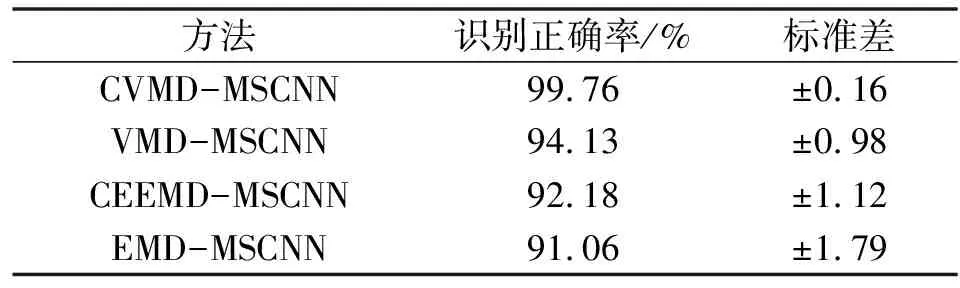
表3 不同降噪方法的性能

由表2和表3可知：文中所提CVMD-MSCNN模型具有更高的故障识别准确率(99.76%)和更小的标准差(0.16)；IRN相比于SAE一定程度缓解了梯度消失现象，诊断准确率有所提升；若不对振动信号进行降噪处理，则模型准确率仅92%；EMD及其变体方法相对VMD和CVMD，模态混叠较为严重，因此降噪效果较差；CVMD由于添加了白噪声对，相比于VMD、CVMD对噪声的鲁棒性更强。图11所示为CVMD-MSCNN的训练损失值，可见模型已收敛。

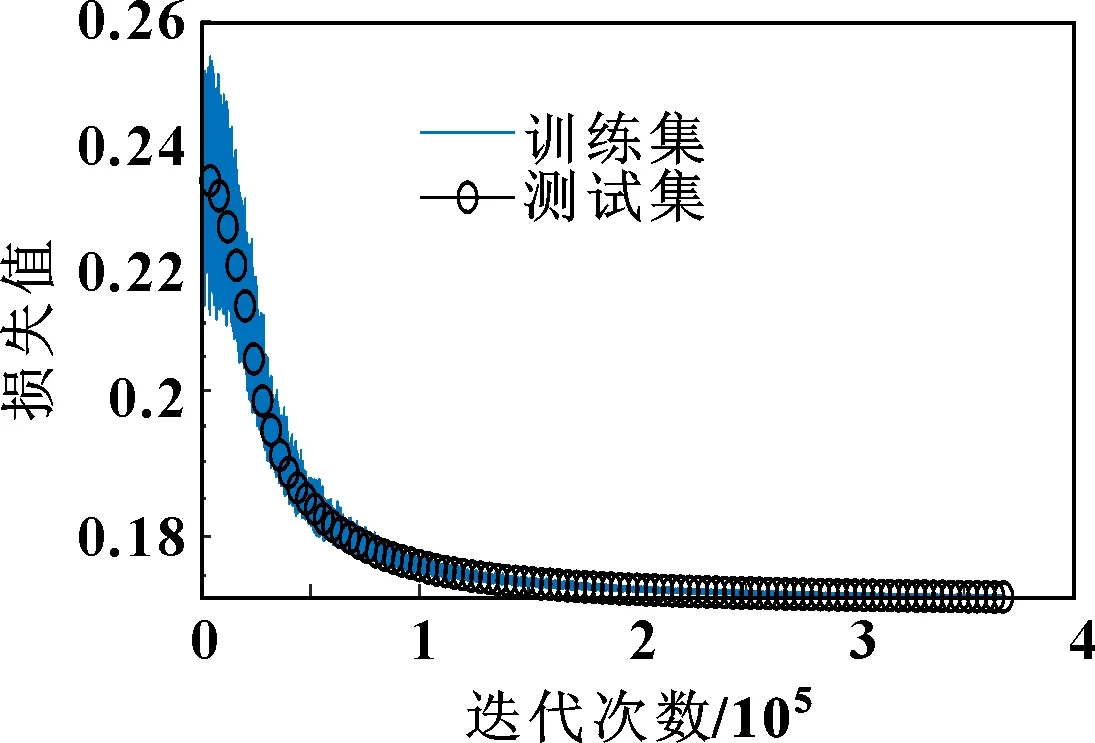
图11 CVMD-MSCNN模型损失函数迭代图

3.4 不同训练样本比例对故障诊断准确率的影响

由文献[16]可知，训练样本比例低会引起MSCNN网络欠拟合，训练样本比例高会引起MSCNN过拟合。图12所示为训练集样本占比60%～90%时，CVMD-MSCNN模型的故障诊断准确率。

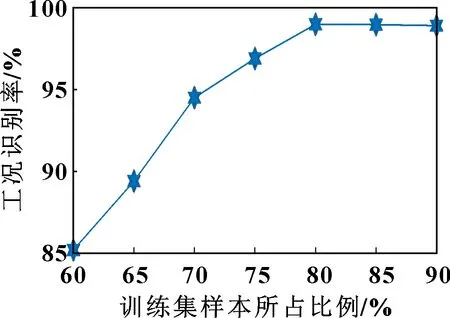
图12 不同比例训练集对CVMD-MSCNN性能的影响

由图12可知：训练样本占比80%以上时，CVMD-IDEA模型的故障诊断准确率已不再上升，故文中选取80%的训练样本。

3.5 深层特征评价

为进一步评价MSCNN网络学习到的深层特征的质量，首先计算类间与类内协方差矩阵和。代表不同工况的离散程度，代表同一工况的聚类度。越大且越小表明特征具有较强的类区分度，和的详细计算见文献[17]。采用文献[18]的3个评价指标对MSCNN学习到的顶层特征质量进行定量计算，公式如下：

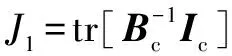
(17)

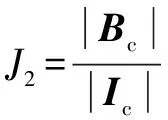
(18)

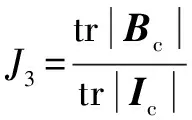
(19)

式中：tr()表示取迹操作。3个指标结合了和的综合信息，计算结果如表4所示。其中 (= 1，2，3)越大代表工况识别结果越好。

表4 不同深度学习模型顶层特征的定量评价

由表4可知:基于MSCNN模型的顶层特征的3个评价指标都大于其他深层模型，表明MSCNN学习到的顶层特征存在着最大的和最小的，更有利于故障诊断。

3.6 不平衡数据集对模型性能的影响

以正常工况与故障工况的样本比例为8 000∶5 000为例，定量计算CVMD-MSCNN、CVMD-MSSFFDCNN和VMD-MSCNN在不平衡数据集下的值，计算公式如下：

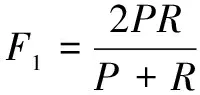
(20)

式中：为准确率;为召回率;在[0，1]之间，0代表最差，1代表最好。表5列出了3种模型的值。

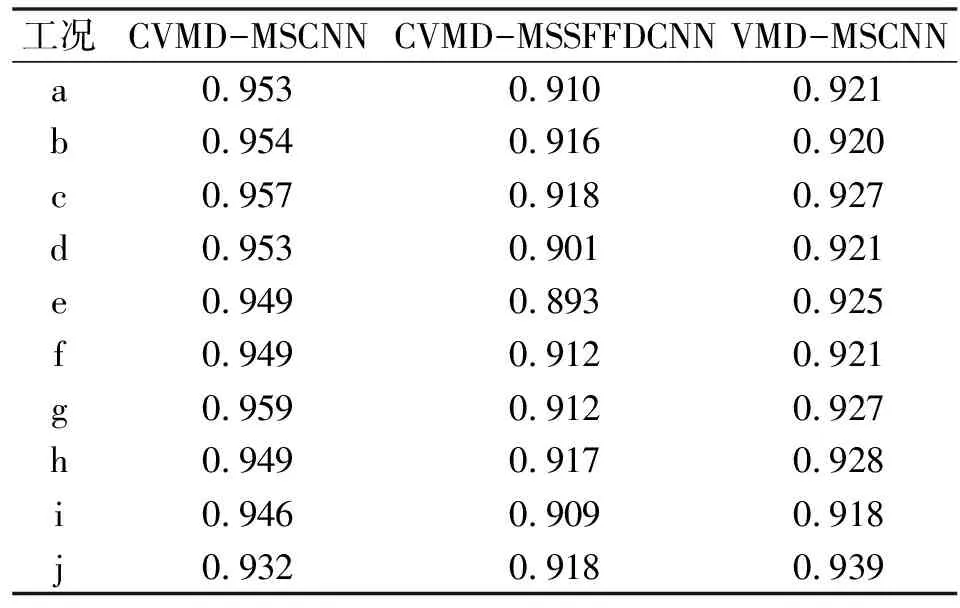
表5 不同模型的F1值

由表5可知：文中所提CVMD-MSCNN模型的指标值较高，进一步验证了CVMD-MSCNN模型的有效性。

3.7 噪声对模型性能的影响

通过在轴承振动数据中添加不同SNR的白噪声而进行对比实验。实验编号及模型如表6所示，表7所示为相应的对比结果。

表6 实验名称及方法

表7 不同模型在不同白噪声下的诊断性能 单位:%

由表7可知：文中所提CVMD-MSCNN模型相比于其他方法，在不同信噪比下的故障诊断准确率更高，进一步验证了CVMD-MSCNN的优越性。

4 结论

本文作者提出一种基于CVMD-MSCNN的轴承故障识别方法，具有较好的故障诊断效果，主要结论如下：

(1)所提出的CVMD方法借鉴了CEEMD的思想，在信号中添加白噪声对，利用VMD将信号分解为若干IMFs并进行集成平均，能较为准确地分解实际信号，对噪声鲁棒性较强，为后续的MSCNN自动特征提取与故障诊断提供了优秀的训练样本；

(2)所提出的MSCNN模型为不同位置的传感器通道分配不同大小的卷积核，增强了模型的故障特征提取能力和故障诊断能力；

(3)后续应进一步研究VMD更有效的分解方法和MSCNN更有效的训练方法。