表面摩擦因数对颗粒螺旋输送动力学特性的影响

许志洋，孟凡净，丁昊昊

(1.铜陵职业技术学院机械工程系，安徽铜陵 244061; 2.河南工学院机械工程学院，河南新乡 453003；3.西南交通大学机械工程学院，四川成都 610031)

0 前言

随着我国工业和农业的发展，在大型港口和农业生产过程中需要使用螺旋输送机输送颗粒体状货物，比如粮食、矿石、化肥以及水泥散体物料等。在螺旋输运过程中，要求输运过程稳定和有较高的输运效率。

螺旋输送机输运颗粒物体过程中，既表现出类似流体的特性，也能呈现出类似固体的特征，具有不稳定的力学性能和多变的结构特性。YAN、XIU等利用离散单元方法，建立了颗粒流润滑的离散元数值模型，对颗粒润滑状态下的非线性行为以及力链的变化特性进行了研究，阐明了颗粒流润滑的动力学特性。MENG等建立了颗粒物质双轴压缩的数值模型，研究了宏观力学行为、微观力学响应和颗粒系统的力链分布受颗粒摩擦的影响规律；结果表明，颗粒摩擦对颗粒系统的应力应变响应、膨胀系数和峰值强度均有显著影响。HARTHONG等通过将连续介质力学模型和微观尺度上颗粒接触力学特性研究结合，通过改善颗粒接触模型和优化压制工艺，提高了粉末冶金压制中处理高密度压制问题的能力。焦杨等人采用离散单元法对湿颗粒聚团碰撞解聚过程中的力学特性进行了研究。

螺旋输送机在输运过程中的散体物料会表现出许多特有的动力学特性，比如运动的不均匀性、剪切膨胀现象以及各向异性等。因此，为了进一步提高螺旋输送机的输运稳定性和输运效率，需要对散体物料在输运过程中的速度波动以及能量进行相关研究。众所周知，摩擦因数是影响接触物体动力学特性的重要因素，然而，螺旋输送过程中输送机摩擦因数对物料速度和能量的影响仍不清楚。

因此，本文作者采用离散单元法建立螺旋输送机的三维离散元数值模型，分析颗粒体输运速度、作用力矩和作用能量随输送机工作面(内、外圆柱面和螺旋面)表面摩擦因数的变化规律。研究结果有助于了解表面摩擦因数对螺旋输送机中颗粒体运动的影响规律，为进一步提高螺旋输送机的输运效率提供理论支撑。

1 离散数值模型的建立

1.1 数值模型

螺旋输送机主要实体结构是由外圆柱面、内圆柱面和螺旋面构成。利用离散单元法软件PFC3D建立螺旋输送机的数值模型，如图1所示，输送机实体结构由线性墙体组成。内、外圆柱墙体长度为4 m，外圆柱墙体直径为 0.5 m，内圆柱墙体直径为0.1 m，螺旋墙体的节距为0.375 m，且该螺旋墙体的外半径和内半径分别为0.25、0.05 m。所有墙体的法向和切向刚度均为5.0×10Pa。为研究输送机工作面摩擦因数对颗粒动力学特性的影响，墙体的表面摩擦因数取值为0.2、0.3、0.4、0.6。

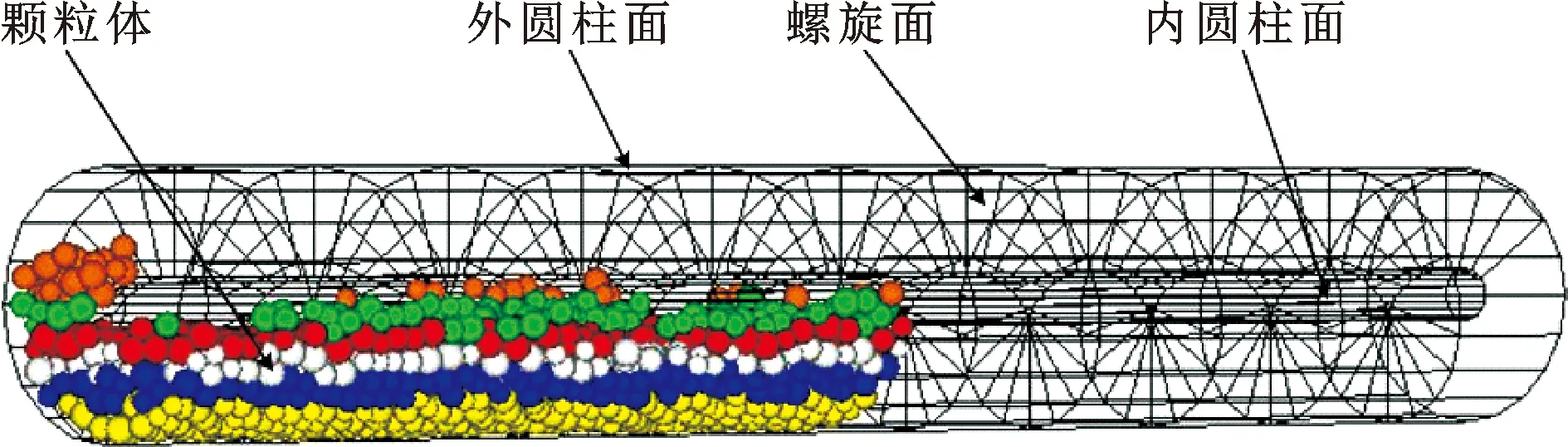
图1 螺旋输送机离散元数学模型

颗粒体由直径在20～30 mm的球形颗粒组成，直径范围服从均匀分布特性。球形颗粒的密度为1.3×10kg/m，球形颗粒表面摩擦因数为0.48。

1.2 数值理论及计算流程

球形颗粒体是离散和不连续的，因此传统的连续介质力学理论无法捕捉它们的主要特性。然而，CUNDALL和STRACK提出的离散单元法成为了解决离散固体颗粒物质系统问题的最有效方法，国内外学者应用该方法进行了一系列的研究工作。离散单元法的基本思想是把离散颗粒考虑为非连续的球形颗粒集合，在初始状态，所有的离散颗粒处于力平衡的状态，但当边界和外部条件改变时，某些颗粒在外部作用力或重力的作用下会产生位移和加速度，并产生新的力学系统。在该过程中，颗粒之间始终处于相互接触的状态，并且引入力-位移定律来对该颗粒物质系统进行研究。公式(1)—(4)以及公式中的参数的具体定义可以参考CUNDALL和STRACK在文献[14]中的论述。

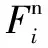
(1)

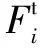
(2)

在此研究中，应用Hertz-Mindlin方法建立接触模型，应用非线性分析方式，采用泊松比和弹性切变模量来进行定义。法向接触刚度和切向接触刚度可以分别表示为

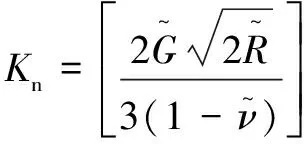
(3)

(4)

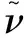
螺旋输送机离散元数值模型的详细计算流程如图2所示。

图2 计算流程

在数值模拟计算前，首先设置外圆柱面、内圆柱面、螺旋面和颗粒体的法向刚度、切向刚度、密度以及表面摩擦因数等参数；然后分别利用墙体生成命令生成外圆柱面、内圆柱面和螺旋面，再利用球体生成命令在螺旋空间中生成随机分布的颗粒球体。然后，对所有球形颗粒施加重力载荷，球形颗粒在重力的作用下在螺旋空间中达到初始平衡状态。随后，对内圆柱面和螺旋面添加沿水平轴方向的旋转速度(60 r/min)，螺旋空间中的颗粒体在螺旋驱动的作用下会沿水平方向自左向右螺旋移动。

2 结果及讨论

2.1 颗粒速度

图3为输运颗粒体在墙体表面不同摩擦因数下的宏观位置状态。可以看出：当表面摩擦因数增大时，出现在更高纵向高度方向上的颗粒体数目越多，这可能与颗粒体的速度波动有关。为了更加清楚地分析该问题，采用定量方法分析了颗粒体的平均速度和速度波动，具体计算如公式(5)—(7)所示：

图3 颗粒体在墙体表面不同摩擦因数下的宏观位置状态

(5)

(6)

其中：<>为所有颗粒体的平均速度；表示第个颗粒在时步时的速度；为颗粒体标号(=1～)；表示时步(=1～100 000)；<>为所有颗粒体在时步的平均速度。

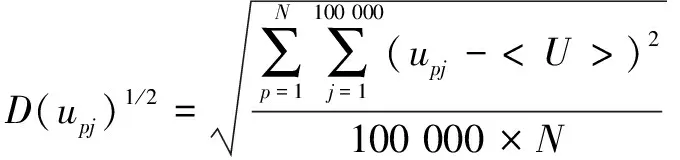
(7)

其中：()12为所有颗粒体的速度偏离平均速度的程度，在数学中表示均方差，但在表示颗粒体的速度变化规律时可以反映颗粒体速度的波动，()12越大，则说明颗粒体的速度波动越大。

图4为不同表面摩擦因数下颗粒体的平均速度<>随时步的变化规律。在不同表面摩擦因数下，所有颗粒体的平均速度<>比较接近。表面摩擦因数=03时所有颗粒体的平均速度<>最大，为0.368 m/s，表面摩擦因数增大到0.6时，所有颗粒体的平均速度<>最小，为0.337 m/s。从图4中还可以看出：随着表面摩擦因数的增大，颗粒体平均速度<>的波动越来越剧烈。

图4 颗粒体的平均速度随时步的变化规律

图5给出了颗粒体的速度波动随输送机墙体表面摩擦因数的变化规律。可以看出：随表面摩擦因数从0.2增加至0.4时，颗粒体的速度波动呈明显增加趋势。但是，当表面摩擦因数增大到0.4以上时，表面摩擦因数对颗粒体速度波动的影响作用越来越小。这说明随着墙体(内、外圆柱面以及螺旋面)表面摩擦因数增大，颗粒体速度波动会增大，速度波动的增大会增加输运过程中的动载荷，从而引起输运过程中振动的增加，增加能耗并降低螺旋输送机的输运效率。所以，选择合适的内、外圆柱面以及螺旋面的表面摩擦因数对提高螺旋输送机的输运效率具有一定影响。

图5 颗粒体的速度波动随表面摩擦因数的变化规律

2.2 螺旋面上力矩和能量

为进一步了解螺旋输送机工作表面摩擦因数对颗粒螺旋输送动力学特性的影响，分析作用在螺旋面和内圆柱面上的力矩和能量。

图6为在不同表面摩擦因数下，作用在螺旋面上的力矩随时步的变化规律。可以看出：作用在螺旋面上的力矩随时步波动，随表面摩擦因数增大，力矩波动更加剧烈。随表面摩擦因数增大，作用在螺旋面上的力矩的平均值也会增大，表面摩擦因数为0.2时，平均力矩为99.2 N·m，当表面摩擦因数增大至0.6时，平均力矩增大到258 N·m。

图6 作用在螺旋面上的力矩随时步的变化规律

图7为作用在螺旋面上的能量随时步的变化规律。可以看出：能量的变化趋势与力矩的变化类似，能量的波动随着表面摩擦因数的增大而变得更加剧烈。能量的大小也随着表面摩擦因数的增大而增大，当表面摩擦因数从0.2增大到0.6时，作用在螺旋面上的能量的平均值也相应地从 623 J增大到1 620 J。

图7 作用在螺旋面上的能量随时步的变化规律

2.3 内圆柱面上力矩和能量

图8为不同表面摩擦因数下，作用在内圆柱面上的力矩随时步的变化规律。可以看出：作用在内圆柱面上的力矩与作用在螺旋面上的力矩变化趋势一致。即，随表面摩擦因数增大，力矩的波动更加剧烈，力矩大小呈增大趋势，当表面摩擦因数从0.2增加至0.6时，平均力矩从0.257 N·m增大到1.55 N·m。

图8 作用在内圆柱面上的力矩随时步的变化规律

图9为作用在内圆柱面上的能量随时步的变化规律。可以看出：作用在内圆柱面上的能量与作用在螺旋面上的能量变化趋势一致。即，随表面摩擦因数增大，能量波动更加剧烈，能量平均值呈增大趋势，当表面摩擦因数从0.2增加到0.6时，作用在内圆柱面上的能量平均值分别从1.61 J增大至9.74 J。

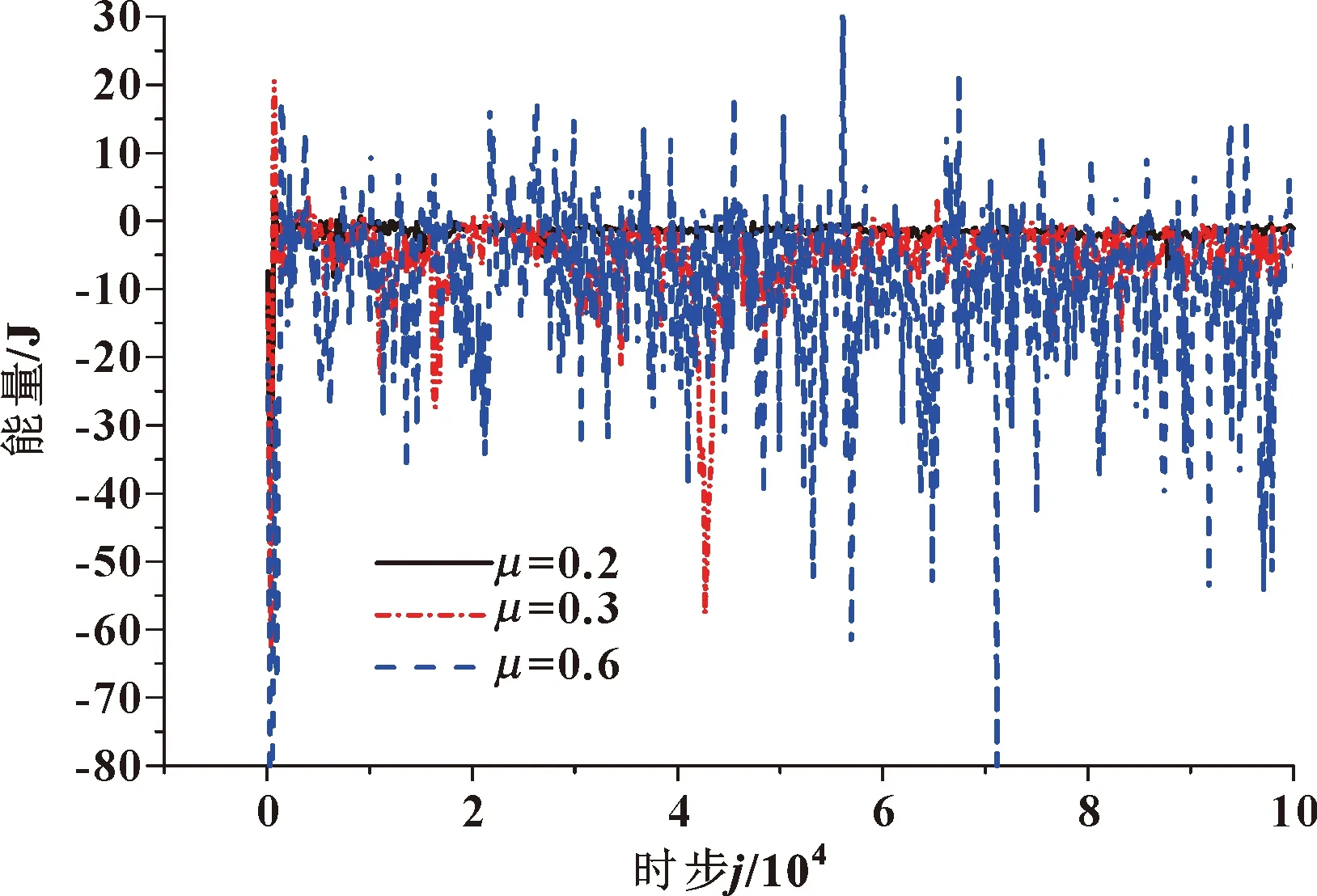
图9 作用在内圆柱面上的能量随时步的变化规律

从以上分析可以看出：随着表面摩擦因数的增大，作用在内圆柱面和螺旋面上的力矩和能量呈增大趋势，力矩和能量的波动更加剧烈。作用在内圆柱面和螺旋面上能量的增大会引起较大的振动。此外，作用在螺旋面上的力矩和能量远大于作用在内圆柱面上的力矩和能量，这说明螺旋输送机在输运过程中的振动主要是颗粒和螺旋面的接触所造成的。因此，合理控制螺旋面的表面摩擦因数可降低作用在螺旋面上的能量，减小输运振动。

3 结论

为了研究表面摩擦因数对螺旋输送颗粒体动力学特性的影响，基于非连续介质的离散单元法建立了螺旋输送机的离散元数值模型，并利用该离散元数值模型研究了表面摩擦因数对颗粒速度、螺旋面和内圆柱面上力矩和能量的影响。得到以下结论：

(1)随表面摩擦因数的增大，颗粒体在螺旋输运过程中的平均速度变化不大，但速度的波动呈现先增大后稳定的趋势；

(2)随表面摩擦因数的增大，作用在内圆柱面、螺旋面上的力矩和能量增大，力矩和能量的波动更加剧烈；

(3)作用在螺旋面上的力矩和能量大于作用在内圆柱面上的力矩和能量，螺旋输送机在输运过程中的振动主要是颗粒和螺旋面的接触所造成的。