基于卡尔曼滤波的UWB与里程计融合定位方法
黄俊杰,李海滨,贾翠玲
(1.内蒙古工业大学材料科学与工程学院,内蒙古呼和浩特 010051;2.内蒙古工业大学工程训练教学部,内蒙古呼和浩特 010051)
0 前言
随着物联网技术的快速发展,工厂、商店、医院等都在走向智能化,人们对定位的稳定性和精度的要求变得越来越高。在室外环境中,依靠全球卫星导航系统(Global Navigation Satellite System,GNSS)如GPS、北斗等与惯性导航系统(Inertial Navigation System,INS)的组合导航可以达到很高的定位精度,但是由于GNSS信号容易受复杂环境影响,在室内无法提供有效的定位数据,因此开发可靠的室内定位系统(Indoor Positioning System,IPS)具有很高的实用价值。
超宽带(Ultra-Wideband,UWB)是利用极窄脉冲传输低功率无线信号的新兴通信技术,时间分辨率高,定位精度可以达到厘米级别,在穿透性、抗多径能力和抗干扰性方面都有着很好的表现,加上高的传输功率和低功耗的特点,所以UWB广泛应用于室内高精度定位。但是同其他无线定位系统一样,数据抖动和非视距环境下的数据失真也是UWB系统存在的主要问题。从动轮式里程计固定在机器人上,结合陀螺仪的角度信息可以对机器人的位置信息进行实时计算,具有结构简单、成本低、短时精度高等优点。从动轮式里程计在短时内有很好的定位效果,但是随着时间增长会产生较大的累计误差,所以单一的里程计模式不适合长时间定位。文献[9]提出了一种结合马尔可夫链和指纹匹配算法的UWB技术,是一种解决NLOS(Non-Line of Sight)误差问题的有效方法,但是需要先对UWB的数据在指纹数据库中进行匹配,计算量过大。文献[10]提出了一种基于UWB、里程计和RGB-D融合的室内定位方法,使用了加权平均的思想,成功将误差抑制在10 cm以内,但并没有对UWB处于严重非视距状态下的情况进行处理。文献[11]提出了一种基于改进自适应加权数据融合的粒子滤波定位算法,与扩展卡尔曼融合算法相比其定位精度提高了15%以上。文献[12]通过求解LiDAR(Light Detection and Ranging)定位信息与粒子之间的几何距离来更新粒子的权重,从而弥补UWB的非视距误差。但是这2种方法都没有对严重非视距状态进行判断,而且没有对IMU(Inertial Measurement Unit)和LiDAR的累计误差进行判断和消除,导致系统长时间运行效果不好。
针对上述问题,本文作者提出一种基于卡尔曼滤波的UWB和里程计数据融合的定位方法。该方法将里程计短时精度高和UWB长时误差有界性的优点进行融合,有望在单片机上实现长时高精度定位。作者先以里程计的数据作为参考量对UWB数据进行非视距情况的判断;然后使用卡尔曼滤波算法对里程计和UWB数据进行不同信赖度下的融合;再使用融合后的数据对里程计数据进行累计误差的判断和修正,来减小里程计的累计误差,提高系统长时间运行的精度和稳定性,以实现长时高精度定位。
1 传感器原理及误差产生原因
1.1 超宽带定位
1.1.1 定位算法原理
UWB基站和标签使用双向飞行时间法(Two Way-Time of Flight, TW-TOF)可以得到基站和标签之间的距离,如图1所示。

图1 TW-TOF测距方法 图2 三边定位算法原理
标签在时刻发射请求性质的脉冲信号,基站在时刻接收到信号,在时刻发射一个响应性质的脉冲信号,标签在时刻接收到,由此可以计算出信号总飞行时间和处理时间。无线电传播速度为光速,则可以得到两模块的距离。

(1)
在超宽带定位过程中,采用三基站一标签的定位方法,使用三边定位算法得到标签的坐标信息,如图2所示。
假设标签的坐标是(,),第个基站的坐标是(,),基站到标签的距离是,此时二维模型下标签坐标满足式(2):

(2)
将式(2)各公式进行平方后得到一个非线性方程组,用方程组中的前-1个方程减去第个方程,整理后得到线性方程组=
其中:

(3)

(4)
使用最小二乘法求解方程可以得到标签坐标:
=()
(5)
1.1.2 非视距误差产生原因
当UWB信号传播遭到障碍物的阻挡而无法直线传输时,就会出现UWB定位的非视距问题。在非视距传播情况下,信号只能穿透障碍物或者借助反射、折射和衍射的方式进行传输,使得到的信息含有大量失真信号,严重影响三边定位算法的计算精度。
1.2 轮式里程计定位
轮式里程计定位系统由图3所示的正交从动轮式里程计和一个JY61六轴陀螺仪组成,轮式里程计由2个正交的全向轮和2个光电编码器组成,由陀螺仪来提供姿态角。

图3 正交从动轮式里程计
将里程计固定到移动机器人底盘上,里程计的2个全向轮相对于移动机器人车体中心的垂直距离分别为和。计算单个采样周期内机器人的位移坐标增量,然后积分,从而得到机器人相对于参考坐标系的位姿状态。如图4所示,在一个采样周期内,2个光电编码器测得2个全向轮旋转轨迹的增量为d和d。机器人相对于机器人车体坐标系的位移增量分别记为d和d,可以由d和d以及机器人旋转角与、等参数表示。机器人相对于参考坐标系的位移增量分别记为d和d,可由d和d及机器人旋转角表示。机器人的旋转角度为可由JY61六轴陀螺仪给出。

图4 机器人移动姿态
最后将d和d进行积分,得到机器人相对于参考坐标系的位姿信息(,,)。

(6)
轮式里程计的数据具有信号频率高、短时精度高的特点,但是如果不经过校核,容易产生较大的累计误差。
2 基于卡尔曼滤波的数据融合定位系统
轮式里程计配合JY61六轴陀螺仪通过公式(6)可以得到机器人位姿信息,短时精度高,但是长时会有较大的累计误差,数据可信度降低。UWB可以得到一个没有累计误差的坐标信息,视距情况下可维持10 cm左右的定位精度,但在非视距环境下会出现数据失真导致数据可信度降低。基于里程计短时精度高和UWB长时误差的有界性,将2种信息进行有机融合以达到长时高精度定位的目的。首先用轮式里程计所得数据作为参考量,对UWB进行状态判断,判断UWB是否处于视距环境中;再使用卡尔曼滤波算法对里程计和UWB进行不同信赖度下的融合;然后使用融合得到的数据对里程计数据进行累计误差的判断与修正,从而降低里程计的累计误差,提高系统定位精度。数据融合的计算流程如图5所示。

图5 数据融合的计算流程
2.1 判断UWB状态
先对UWB数据进行一次一阶低通滤波,以初步减小数据的抖动,然后分两层对UWB数据状态进行判断。
第一层先对UWB的单点数据进行判断,需要获知UWB基站是否得到标签的距离信息,因为在定位中可能出现障碍物引起基站无法得到标签信息的情况,使三边定位算法不能正常使用,导致UWB数据失效。通过第一层的判断可以排除无法得到单点数据的情况,如能得到单点数据则进入第二层判断。
在第二层中对UWB数据做是否进入非视距状态与非视距程度的判断。用当前的UWB数据对里程计的数据求距离偏差,在里程计的数据上设定多层环形区域,通过判断UWB所属区域对非视距程度进行分类量化,为后续数据融合提供依据。将UWB所处状态分为3类,则有式(7)所示分类量化结果。

(7)
式中:为第类视距状态,其中=(1,2,3);表示状态阈值;为距离偏差值。表示UWB处于视距状态,因为文中实验使用的UWB系统的定位精度为10 cm,所以取值可在15 cm左右,但是不能小于UWB本身的定位精度。表示UWB处于轻度非视距状态,这个非视距状态的数据尚可以使用,具有一定的可信度,表示允许使用的非视距状态误差距离的最大值。表示UWB已经处于严重的非视距状态,数据已经完全不可信。经过上述两层判断,实现了以里程计为参考量的UWB非视距程度的分类量化。
在上述工作基础上,将对里程计数据和分类量化后的UWB数据进行数据融合。
2.2 基于卡尔曼滤波算法的数据融合
卡尔曼滤波的数学模型包括预测模型和观测模型2个部分,离散化的形式如式(8):

(8)



(9)

(10)


(11)

(12)

(13)
在上述卡尔曼滤波算法公式中已省略对单位矩阵的书写。
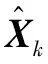
用式(7)分类量化的结果设置参数,表示UWB数据处于视距状态,则和可以设置为相同的值,即设里程计和UWB值具有相同的可信度,这对参数使用、表示。表示UWB处于轻度非视距状态,则通过增大、减少来提高系统对里程计的信赖度,这对参数用、来表示。表示UWB处于严重非视距状态,UWB数据失去作用,此时系统以里程计数据为准,设置为单位矩阵,设置为零矩阵,此时=、=。综上所述,将UWB的视距状态与和的参数取值归纳为式(14)。

(14)
在UWB处于不同状态下使用式(14)改变预测值噪声的协方差和观测值噪声的协方差,从而改变融合系统对观测和预测的信赖程度,进而达到自适应的效果,提高了系统的稳定性。
2.3 里程计累计误差的判断和修正
使用融合后的数据来判断里程计的累计误差。以得到的融合后的数据为圆心设定一个圆形许用区域,通过判断里程计数据所在区域对里程计累计误差进行判断。如果里程计的数据连续多次超出圆形许用区域,则表明里程计已经产生了较大的累计误差。设定的圆形许用区域半径越大则对里程计的累计误差的容忍度越大,圆形许用区域半径越小则对里程计的修正会越灵敏。但实验使用的UWB的定位精度为10 cm,视距情况下的数据融合对里程计和UWB信赖度相同,融合后的数据在两者之间,所以圆形许用区域的最小半径不能小于5 cm。

(Corrected)=(orignal)+
(15)
再用修正的里程计的数据参与数据融合,从而提高系统长时定位的精度。
3 仿真与实验验证与分析
3.1 仿真实验
仿真实验使用开源机器人仿真软件Webots,仿真机器人由全向运动底盘、轮式里程计和UWB定位系统组成。其中全向运动底盘和轮式里程计通过在Webots中直接建模生成,UWB定位系统使用软件中的GPS传感器通过设定传感器的噪声来模拟产生不同状态的UWB信号。仿真机器人模拟完成如图6所示的蛇形运动,先向轴正方向运动3 m,然后向轴正方向运动1 m,向轴负向运动3 m,轴正向运动1 m,如此反复,得到的数据如图6—图7所示。
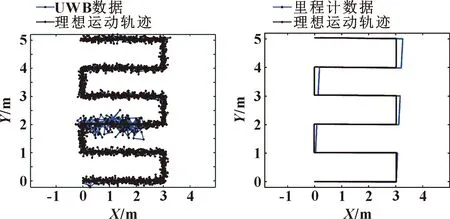
图6 理想轨迹与UWB数据形成的轨迹 图7 理想轨迹与里程计数据形成的轨迹
图6为UWB数据的轨迹图,可以看出:机器人从(0,2)到(2,2)的运动期间设定UWB为非视距状态,具体表现为UWB数据抖动幅度变大。图7为里程计数据的轨迹,里程计在运行过程中产生了累计误差,随着时间的增加误差也在增加。
图8为最终融合得到的数据,系统成功判断出UWB的状态,并进行了不同信赖度的融合,得到稳定的数据。并且在(3.057,2.625)m点处融合后的数据判断出里程计的累计误差,并对里程计数据进行了修正。然后使用修正过的里程计数据继续与UWB进行融合,减小了融合后数据的累计误差,提高了系统长时间运行的稳定性。

图8 理想轨迹与最终融合后数据的轨迹
图9为每个UWB原始数据与理想位置坐标的误差和每个融合后数据与理想位置坐标的误差对比,可以看出:融合后的数据相对于UWB原始数据的抖动和误差都明显减小,而且在非视距情况融合后的数据依然有很好的稳定性和准确性。融合后的数据误差会随着时间的增加逐渐变大,这是由于里程计的累计误差逐渐增大所致,但当里程计的累计误差达到一定程度时,又会通过融合后的数据对里程计数据进行修正,从而将里程计数据的累计误差控制在一定范围之内。UWB原始数据的平均误差为0.101 5 m,融合后的平均误差为0.048 3 m,融合后的数据误差减少了52.41%,达到了良好的预期效果。
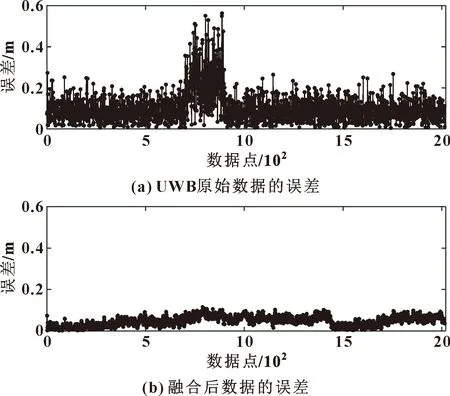
图9 UWB原始数据的误差和融合后数据的误差对比
3.2 实验验证与分析
为进一步验证文中方法在单片机系统中的应用效果,拟开展实物机器人定位实验研究。实验采用基于Decawave公司的DW1000芯片的UWB产品,该产品定位范围为50 m,组成的系统定位误差为10 cm左右。采用的轮式里程计为自制的正交从动式轮式里程计如图3所示,平均运行10 m会产生5 cm的累计误差。JY61六轴陀螺仪采用TDK公司的MPU6050姿态传感器,通过JY61的处理器读取MPU6050的测量数据然后通过串口输出,静态测量精度稳定在0.05°,动态精度为0.1°。实验场景为9 m×21 m的实验室,由3个UWB基站组成一个等腰三角形,所有基站在距地面高为2.40 m的同一平面上,UWB标签置于机器人顶端。机器人实物系统如图10所示。

图10 实验机器人的图片
实验分为5组,每组做5次实验,每组实验分别为单独使用轮式里程计、在视距情况下单独使用UWB、在视距情况下进行文中方法的融合、在存在8 m非视距情况下单独使用UWB、在存在8 m非视距情况下进行文中方法的融合,以所得实验数据分别作为定位坐标进行运动控制。利用UWB标签加盖来产生非视距情况。
理想实验轨迹与仿真时的相同,一次实验共运行20 m,平均运行时间为59.82 s,其中2~10 m区间段为产生非视距的区域。机器人以stm32f103单片机为控制器,进行数据处理和机器人控制。机器人每10 ms进行一次闭环纠偏,每次的纠偏距离是机器人当前坐标与终点和起点直线的垂直距离,即当前机器人偏离目标位置的距离。机器人将用这个偏离的距离作为输入量,使用PID算法对机器人进行轨迹纠偏,以保证机器人回到目标路径上。总纠偏距离可以反映机器人一段时间内运动的平稳性,总纠偏距离越小表明机器人运动越平稳,纠偏距离为零表示机器人保持在理想路径之上。将所得实验数据列于表1。
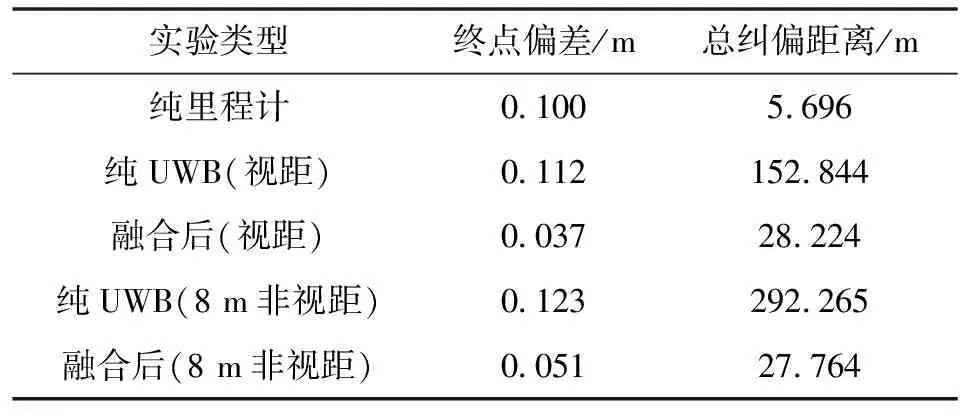
表1 得到的5组数据
由表1可以看出:单独使用里程计的数据运动20 m平均产生了100 mm的终点偏差,这个误差是长距离运动导致的累计误差,且这个误差会随着运动距离的增加而增加,但里程计数据稳定,总纠偏距离只有5.696 m,机器人运行平稳。
使用纯UWB数据进行定位的机器人运动过程中抖动极大,尤其是在非视距状态下UWB数据极不稳定,终点偏差分别为112、123 mm,在视距状态下运动20 m平均产生了152.844 m的总纠偏距离,在存在8 m的非视距状态下运动更是平均产生了292.265 m的总纠偏距离,这表明单独使用UWB数据不适合机器人定位。
使用文中算法在一直处于视距状态下运动20 m终点偏差为37 mm,平均总纠偏距离为28.224 m,机器人运行较平稳。在存在8 m的非视距环境中运动20 m,终点偏差为51 mm,平均总纠偏距离为27.764 m,系统成功判断出UWB是否处于非视距状态并自动进行了不同信赖度的数据融合,大幅减小了UWB数据的抖动,并且将里程计数据的累计误差控制在一定范围内,得到的数据稳定且精度较高。相比单独使用UWB的数据,在视距环境中稳定性提高了81.5%,精度提高了67.1%;在存在8 m非视距的环境中稳定性提高了90.5%,精度提高了59.2%。由此可见,使用文中融合方法可以大幅提高定位系统的稳定性和精度。
4 结论
本文作者利用里程计的短时精度高和UWB的长时误差有界性,提出了一种基于卡尔曼滤波的数据融合方法,成功地将2种信息有机融合达到了长时高精度定位的目的。通过软件仿真和实验验证表明:在UWB一直处于视距环境中融合后的数据相比单独使用UWB的数据稳定性提高了81.5%,精度提高了67.1%;在存在8 m非视距环境中,相对于单独使用UWB的数据稳定性提高了90.5%,精度提高了59.2%。系统运行稳定,实现了长时间连续可靠的定位,具有较大的工程应用价值。

