基于地质单元体的微动信号频散曲线反演

赵红鹏何登科洪雨

1.中国矿业大学(北京)地球科学与测绘工程学院,北京 100083;2.煤炭资源与安全开采国家重点实验室,北京 100083

微动勘探技术是一种从环境微动信号中提取面波频散曲线进而分析地下介质物性差异的勘探方法[1]。城市微动勘探方法利用天然或人为因素所造成的环境地面振动作为源数据进行分析,是一种经济成本低、勘探效率高、受工区地形影响程度小、符合绿色发展理念的方法,在工程地震领域获得了广泛的应用[2]。微动信号是一种包含体波与面波的复杂振动信号[3-4],信号中面波能量占70%以上。对微动信号的进一步分析,可以提取出面波频散曲线。

从微动信号中提取面波频散曲线后,分析频散曲线能够得到地下介质物性参数[5]。对于频散曲线的分析,早期人们做过许多工作,如半波长解释法、一次导数极值点法和拐点法等[6]。但这些方法主观性强并不可靠。Xia 等[7]采用 LM(Levenberg-Marquard)算法与奇异值分解技术进行反演,得到了近地表横波速度,但该算法受初值影响较大。为了解决这一问题,宋先海等[8]提出等厚薄层权重自适应迭代阻尼最小二乘法。该算法在一定程度上解决了初值的选取问题,却使反演时未知参数增多、方程的欠定程度加大,并且在反演过程达到一定稳定性后还要进行冗余计算。此外,Yamanaka 等[9]提出了遗传反演算法,蔡伟等[10]提出基于萤火虫和蝙蝠群的智能算法,Beaty 等[11]使用模拟退火算法进行高阶面波频散曲线的反演,Shirazi 等[12]通过人工神经网络算法进行频散曲线反演以进行路基检测,Song 等[13-14]先后将粒子群优化、模式搜索算法应用于频散曲线反演。这些算法在一定程度上能够得到比较好的解,但都依赖初始参数的设定,仅在某些特定情况下适用,同时存在占用内存多、计算开销大等问题。

等厚薄层权重自适应迭代阻尼最小二乘法能够在一定程度上摆脱反演对初值的依赖,这是遗传算法等不具备的优势,但该算法增加了反演过程中未知数的数量,使反演方程的欠定程度增大,同时密集的地层划分也会使反演计算开销大、收敛速度慢。为了解决这些问题,本文基于地质单元体[15]的合并思路对宋先海等提出的等厚薄层权重自适应迭代阻尼最小二乘法做出改进:当反演收敛速度较低时,对横波速度相差较小的相邻地层进行合并,以合并后的横波速度参与反演,从而保证在计算开销不大的前提下,使反演过程中未知数的个数尽量少、降低方程欠定程度,以得到更加稳定准确的解。

1 微动信号频散曲线提取

从微动信号中提取频散曲线的方法有频率波数法[16]、空间自相关(Spatial Auto Correlation,SPAC)法等。其中,空间自相关法由Aki[17]提出,近20年引起了人们的关注[18],通过反演频散曲线可以估算地层横波速度结构,这是目前公认最有效、快捷的确定横波速度结构的方法之一[19]。

SPAC 法从微动数据提取面波频散曲线时有2点假设:

(1) 微动在时间与空间上是平稳随机过程。

(2) 基阶面波在微动包含的各种波中占主导。

SPAC 法一般采用圆形的台站布设方式,在圆心处布设一个台站,并以r为半径布设n个台站。如图1所示,在圆心O处布设一个台站,在r为半径的圆上布设3 个台站,这样的布设方式能够保证采集的微动信号入射方位均衡。

图1 微动观测台站示意图Fig.1 Microtremor observation array

通过对微动数据进行傅里叶变换[20],采用式(1)的计算方法在频率域计算空间自相关系数,该方法具有较高的计算速度与精度。

式中,ω为角频率;r为两个台站间的距离;ρ为空间自相关系数;∗代表复数共轭;S为对台站数据进行傅里叶变换的结果。

空间自相关系数的值近似第一类零阶贝塞尔函数:

式中,J0为第一类零阶贝塞尔函数;c(ω)为相速度。

对空间自相关系数进行贝塞尔函数拟合,即可得到固定频率下的相速度c,从而获得频散曲线。

2 基于地质单元体的改进算法

层状介质中面波频散方程为非线性过程[21],表示为隐式方程:

式中,fj为第j个频率;VRj为第j个频率的相速度;m为频率个数;Vis、Vip、ρi、Hi(i=1,2,…,n)分别为第i层的横波速度、纵波速度、地层密度和厚度;n为地层层数。

将地层划分为多个薄层能够一定程度上摆脱对初始模型的依赖,但却使反演过程未知参数增多。过多的未知参数不仅影响方程的稳定性、降低解的精度,也会带来冗余计算。实际上属于同一地层的薄层具有相似的物性参数,在反演过程中可以合并这些地层,用合并后的地层参与反演。

给出阈值ΔV,当i+1 层与i层横波速度差

时,有

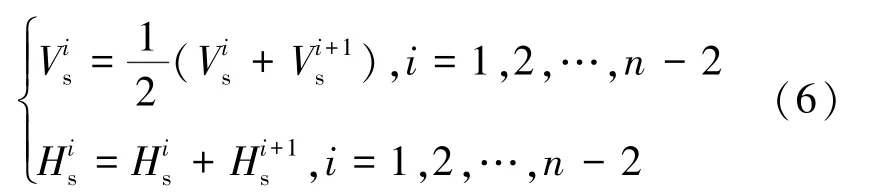
频散方程对密度和纵波速度的变化不敏感,在反演时密度与纵波速度用经验公式(7)[22]计算得到:

基于式(5)～式(7)简化频散方程:

利用泰勒级数将式(8)线性化:

式中,ΔVs为反演过程中的横波速度修正量;ΔVR为对应的相速度修正量;J为雅可比矩阵,以差分求得[23]。

目标函数应兼有方差项和模型长度项两项内容,因此将目标函数定义如下:

式中,‖‖为L2 范数;τ为阻尼系数。

式(10)的解为

式中,E为单位矩阵。

式(11)在反演过程中不断迭代,迭代时取

迭代时根据相邻两次迭代横波速度的内积大小动态调整τ。

完整的改进算法流程如图2所示。该算法在等厚薄层权重自适应迭代阻尼最小二乘法的基础上做出修改,首先进行细化分层并输入横波速度初值,计算频散方程得到初值对应的相速度,之后计算相速度与实测值的差,通过差分的形式求出雅可比矩阵,最后计算横波速度的修正量。对于第k次反演,比较第k次反演与k-1 次反演修正量的大小,通过比例因子I调整阻尼系数。

图2 改进算法流程Fig.2 Flow chart of improved algorithm

在每一次迭代之后判断相速度差是否满足条件,若第k次相速度差大于阈值ε1,但第k次目标函数差小于阈值ε2,则说明反演已进行到中后期,收敛速度减缓。此时将每个地层视为一个地质单元,将横波速度之差小于阈值ΔV的两单元合并,以新的单元参与第k+1 次反演。若第k次相速度差小于阈值ε1,便结束反演,得到最终横波速度模型。

3 算法应用

3.1 模拟数据

给出两个5 层地质模型。表1是含低速夹层模型对应的参数,表2是含高速夹层模型对应的参数。表1中第3 层是低速层,厚12 m,表2中第3层是高速层,也是12 m。表1与表2中的纵波速度、密度等参数由式(7)计算得到。

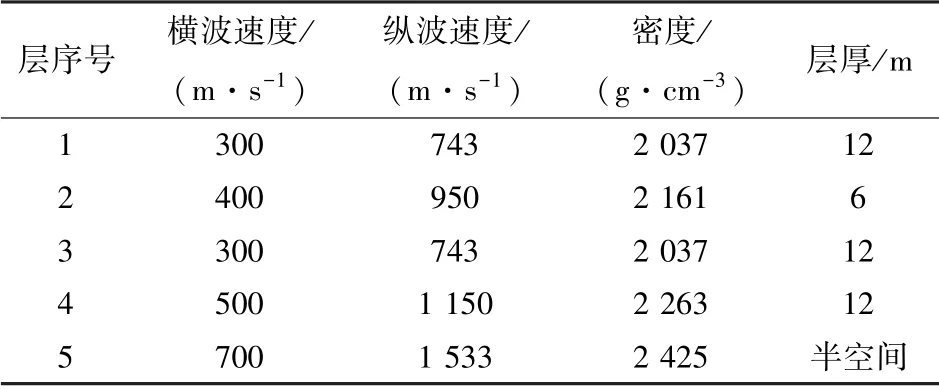
表1 含低速夹层模型参数Table 1 Parameters of the model with low velocity interlayer

表2 含高速夹层模型参数Table 2 Parameters of the model with high velocity interlayer

在实际情况当中,地下介质的层厚等信息往往不得而知,反演时选取的初始薄层厚度有两种情况,一是层厚恰好为薄层的整数倍,二是不成整数倍。为了尽可能贴近实际情况,设置2 组初始参数进行反演:第1 组参数中2 个模型均将地层划分为20 层,每层3 m,每层初始速度设置为375 m;第2组中两个模型每层均为2.5 m,共24 层,每层初始速度同样设置为375 m。第1 组参数中层厚是每个薄层的整数倍,第2 组参数中的层厚与薄层不是整数倍关系。

图3是含低速夹层模型在两组参数下经原算法与改进算法反演50 次之后的结果。

图3 模型1 反演结果Fig.3 Inversion results of model 1

图3中,改进算法的结果与模型值的平均误差为4.5×10-12m/s,基本与模型值无差别。原算法的平均误差为28.0 m/s,横波速度在深度超过10 m以后与模型值存在较大差别。图3(b)改进算法平均误差为8.3 m/s,原算法为32.1 m/s,改进算法得到的横波速度与模型横波速度在12～18 m 处存在差距,但总体来看改进算法结果更接近模型值。图3中改进算法反演时将地层最终合并为7 层与5 层,层数少于初始的20 层与24 层。改进算法得到的结果中层数较少,即反演方程中的未知参数更少、方程的欠定程度低,所以更容易得到稳定正确的解。

图4显示了含高速夹层模型在2 组参数下经2 组算法反演50 次后的结果。图4(a)中,改进算法的平均误差为1.3×10-12m/s,结果与模型值基本无差别;而原算法平均误差为23.2 m/s,横波速度在深度20 m 以上区域与模型值存在较大差别。在图4(b)中,改进算法的反演结果平均误差为18.7 m/s,原算法平均误差为31.3 m/s。与原算法相比,改进算法的误差更小。图4中改进算法反演时将地层最终合并为5 层与6 层,层数少于初始的20层与24 层。在含高速夹层模型中改进算法能够减少反演时的未知参数个数,降低方程欠定程度,得到更优的解。

图4 模型2 反演结果Fig.4 Inversion results of model 2

由以上模拟结果可知,若地层厚度与初始薄层不成整数倍关系,那么反演是存在固有误差的,无论怎样进行薄层合并都不可能在两地层交界处完美拟合。但是,无论地层厚度是不是初始薄层的整数倍,改进算法都能得到更好的反演结果,当地层厚度与初始薄层是整数倍关系时,改进算法表现会更好。由于先验信息的缺失,在实际勘探当中往往无法使地层厚度为初始薄层的整数倍。这时应在满足勘探精度要求的前提下划分薄层,使地层厚度更接近整数倍薄层,减小反演结果在两层交界处的误差。

3.2 实测数据

在北京某高校内采集微动数据,所采用的台站布设方式如图5所示,在圆心处布设一个台站,在半径为r与半径为R的圆周上各布设3 个台站,r取3.5 m,R取7 m。

图5 台站布设方式Fig.5 Station layout

在计算频散曲线之前首先对原始数据进行预处理,主要有去均值、去线性趋势及带通滤波等。

图6为7 个台站采集的微动数据和预处理的结果。这7 道微动数据在波形上具有一定的相似性,空间自相关系数的计算正是基于波形间的相似性。

图6 原始微动数据及处理后数据Fig.6 Original microseismic data and processed data

根据图5的台站布设方式,能够确定5 组不同半径的台站组合。每种组合下各有3 组台站对(表3)。

表3 台站组合Table 3 Station combination

将5 种台站组合的数据分别代入式(1)得到5条空间自相关系数曲线,如图7所示。用第一类零阶贝塞尔函数拟合该结果即可得到频散曲线。对5 种组合下得到的频散曲线[24-25]进行平均处理,结果如图8所示。

图7 空间自相关系数Fig.7 Spatial autocorrelation coefficient

在数值实验中给出了2 个分层较明显的模型,在实际情况中遇到的更多对象,层间介质速度可能是连续变化或差异很小的。此时采用改进算法进行反演时,应根据勘探精度要求划分初始薄层,反演过程中在保证获得更优频散曲线拟合度的同时进行地层合并。反演实测频散曲线时,将地层划分为120 层,每层0.5 m,各层横波初值均为350 m/s。如图8(a)所示,反演50 次时原算法与改进算法得到的频散曲线值,与实测频散曲线值在低频部分稍有差距,在高频部分基本一致。从频率3 Hz 和7 Hz 位置处的放大图来看,改进算法得到的频散曲线值更接近实测值。

图8 实测数据反演结果Fig.8 Inversion results of measured data

图8(b)中通过原算法与改进算法得到的横波速度的变化趋势基本一致,地层横波速度随着深度的增加先增大、后减小再增大,这与实际情况相吻合。该高校在地下15 m 左右为含水层,介质中含水率过高导致横波速度降低,因此呈现出含低速夹层的现象。地层15 m 以上为上覆土,横波速度大于含水层,在30 m 以下是基岩,横波速度较大。

使用原算法反演时层数一直是120 层。而在使用改进算法反演时,层数在第17 次迭代中由120 层合并为18 层,这有效地减少了反演过程中的未知参数,降低了反演过程中方程的欠定程度,所以在图8(a)中改进算法拟合程度更好。

原算法与改进算法反演时的迭代误差如图9所示。迭代误差由实测相速度与反演相速度的平均绝对差值表示。改进算法在第17 次迭代中才开始进行地层单元合并,在此之前两种算法的迭代误差是相同的。地层合并后,改进算法的误差除了在第18 次迭代时有一个跳变外,之后均小于原算法。而计算开销与层数成正比,所以改进算法的计算开销在第18 次迭代之后同样比原算法小。即改进算法能够以更小的计算开销获得更精确的解。

图9 迭代误差Fig.9 Iteration error

4 结 论

从微动信号中提取面波频散曲线后,采用基于地质单元体的改进算法能够降低反演方程的欠定程度,以较小的计算开销获得稳定正确的反演结果。

(1)在进行频散曲线反演时,将地层划分为等厚薄层能够一定程度上解决初值选取的问题。但地层层数的划分规模与反演过程中未知参数成正比,而过多的未知参数不仅影响方程的稳定性、降低解的精度,而且也会带来冗余计算。

(2)基于地质单元体的合并思路进行算法改进,在反演的中后期对横波速度绝对差值小于设定阈值的两地层单元进行合并,用合并后的地层参与反演,这在降低反演方程的欠定程度的同时减少反演过程的运算量。

(3)将改进算法应用于两个理论模型,反演结果表明,改进算法具有优异的收敛速度及反演精度。将改进算法应用于实测数据,验证了其适用性。

(4)实际勘探中遇到的反演对象层间介质速度往往是连续变化或差异很小的。在采用改进算法反演此类对象时,可根据勘探分辨率要求将反演对象划分为足够薄的层,用划分后的层等效替代真实介质进行反演。

本文改进算法中的地层合并仅在反演的中后期进行,更深入的研究可以考虑根据不同深度的横波速度对高阶频散曲线的敏感程度进行地层合并的判定条件,采用此种方法有望将合并提前。