运动模糊图像PSF 参数估计方法改进及图像复原

高海韬，李丹宁，2，王 彬，唐鑫鑫

（1.贵州大学 大数据与信息工程学院，贵阳 550025；2.贵州科学院，贵阳 550001）

0 概述

图像运动模糊是相机在曝光时被摄物体和相机间发生相对位移导致的一种图像退化现象［1］，成像时相机和被摄物体间发生的相对位移会使得不同位置的像素发生叠加，从而导致成像质量下降。运动模糊作为最常见的图像退化现象之一，广泛存在于众多视觉处理任务中，而高质量的清晰图像是高效完成此类任务的关键，因此，运动模糊图像复原问题一直是国内外学者们关注的焦点。

根据退化图像的点扩散函数（Point Spread Function，PSF）是否已知，可以将图像复原算法分为图像非盲复原算法和图像盲复原算法两类。图像盲复原是在PSF 完全未知的情况下进行图像复原，如基于正则化的方法和基于深度学习的方法。基于正则化的图像复原方法通过设立正则项约束，以引导复原模型在迭代的过程中向符合图像先验和真实清晰图像的方向进行优化。TU 等［2］对图像复原算法的边缘保留正则化项进行改进，减少了由运动模糊引起的边界误差，并通过模糊映射法和下采样插值技术有效提高了算法效率。为了解决多帧超分辨率（Multi-Frame Super-Resolution，MFSR）中的运动模糊问题，MA 等［3］设计一个EM 框架来引导PSF 估计和高分辨率图像重建，并加入L2 正则化项来抑制噪声。基于深度学习的方法利用预先收集的大量训练数据隐式地学习一个从降质图像到清晰图像的映射。王伟鹏等［4］提出一种结合卷积变换与细节优化的图像去雾算法，其采用卷积变换的思想和分段映射后处理操作，并结合大气散射模型实现雾化图像的细节提升。缪斯等［5］提出一种可微分神经网络架构搜索方法，该方法可用于图像盲去模糊时神经网络的参数调节。此外，文献［6-8］首先从退化图像中提取出模糊参数，然后用估计出的PSF 复原出清晰图像。

本文通过分析运动模糊图像的频谱特征，提出一种改进的PSF 参数估计方法，以提高估计结果的精度和有效估计范围，并通过PSF 参数估计和运动模糊图像复原实验来验证所提方法的有效性。

1 相关工作

PSF 求解是图像复原的关键步骤。LEE 等［9］通过运动模糊图像的频域周期性估计PSF 参数，并利用图像后处理技术改善重建图像的质量。ZHU等［10］提出一种利用多幅图像间接估计PSF 的方法，其通过结合多通道PSF 正则项和L1 图像稀疏正则化的最小化代价函数来粗略估计PSF，然后根据PSF的稀疏性和正确率将估计结果进行细化并输出解卷积。MOGHADDAM 等［11］引入模糊集概念，以对基于Radon 变换的PSF 参数估计算法进行改进。

由于实际中相机成像尺寸有限引起的边缘截断破坏了卷积的连续性，使得运动模糊图像的频谱图像中心位置会出现一道十字亮线，如图1 所示，这种十字亮线会对模糊参数的估算造成极大干扰，可能导致估算结果误差过大甚至不可信。

图1 运动模糊图像和十字亮线Fig.1 Motion-blurred image and cross bright line

针对十字亮线干扰问题，研究人员提出了不同的解决方案［12-13］。胡发焕等［14］利用骨架化变换操作细化暗条纹，有效提高了条纹检测精度。乐翔等［15］通过频谱分块切除亮线干扰，将暗亮条纹对比最明显的块图反色后再进行Radon 变换以提取PSF 参数。胡硕等［16］对频谱图像进行自适应形态学滤波以消除亮线干扰，但是，该方法需要设定阈值以对中心亮条纹进行迭代腐蚀，导致其效率和估计精度有限。

2 运动模糊图像退化模型及其频谱特性分析

图像复原［17］是一个病态的反问题，在数学定义上，图像退化是图像与PSF 的卷积过程，图像复原则是这一过程的逆过程［18-19］。若要恢复出清晰的真实图像，必须先建立图像退化模型。图2 所示为空不变系统中运动模糊图像的退化模型。

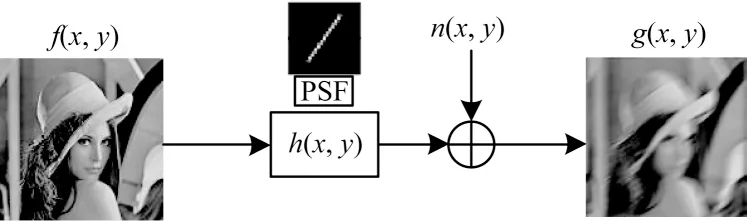
图2 运动模糊图像退化模型Fig.2 Degradation model of motion-blurred image

图像退化模型的时域表示为：

其中：g（x，y）表示退化图像；f（x，y）表示原始图像；h（x，y）表示引起图像模糊的PSF（退化函数）；n（x，y）表示噪声函数；“*”表示卷积运算。

当n(x,y)=0 时，即图像除产生运动模糊外不受噪声干扰，根据卷积定理，式（1）的傅立叶变换（频域表达）可简化为：

在实际运算时，图像分析是二维离散域的处理过程。设图像尺寸为M×N，则原始图像的傅立叶变换为：

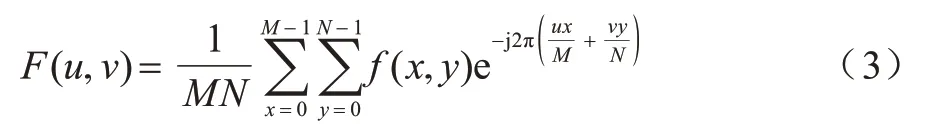
运动模糊图像的PSF 主要由模糊角度和模糊尺度这2 个重要参数定义。假设在曝光时间T内，目标物体相对于摄像机在θ角（运动方向与水平轴正向的夹角）方向上匀速运动，产生的位移为L，则运动模糊图像的PSF 可描述为：

设a和b分别为曝光时间T内像素点在水平和垂直方向上的位移，则h（x，y）的傅立叶变换为：

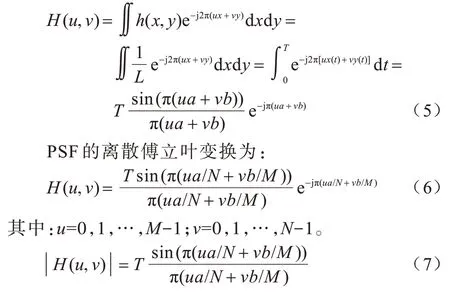
由式（7）可知，|H(u,v)|的表达式中包含sin 函数，由sin 函数性质可知，|H(u,v)|在（ua/N+vb/M）=0时有最大值，|H(u,v)|在（ua/N+vb/M）取非零值时为零。因此，模糊图像的频域上会呈现以下特征：模糊图像频谱图上呈现出亮暗相间的平行条纹，且条纹方向随着模糊角度的变化而相应改变。

设lu和lv分别为运动模糊长度L在垂直和水平2 个方向上的分量，则：

设亮暗条纹相对水平轴正向的倾斜角度为φ，则：

可得条纹的倾斜角度φ与运动模糊角度θ间的关系为：

由式（10）可知，通过检测模糊图像频谱图像中的亮暗条纹倾角φ可以得出运动模糊角度θ。设频谱图中相邻条纹的间距为d，则频谱图像中心第一个条纹的方程式为：

由式（13）可知，当图像尺寸一定时，条纹间距d与模糊长度L呈反比，随着模糊长度的增加，条纹间距减小，条纹数量变多；反之，条纹间距增大，条纹数量变少。

3 运动模糊图像PSF 参数估计方法

根据上文分析可知，通过运动模糊图像的频域周期性特征与模糊参数间的关系，可以估算图像的PSF 参数。但是，由于存在外界限制和环境干扰，对运动模糊图像直接进行傅立叶变换获得的频谱图像往往会存在大量毛刺、噪点以及十字亮线干扰。为了解决这一问题，现有方法一般通过滤波或频谱分块的方式来消除十字亮线和冗余信息干扰，但是，这种方式存在重要信息丢失和残留干扰的问题。现有PSF 参数估计方法主要存在以下2 个方面的局限性：

1）根据Radon 变换原理，在检测中心亮条纹获得条纹倾角时会因亮条纹本身的宽度而导致角度误差，如图3（a）所示，从而使得参数估计结果不够精确。

2）由式（13）可知，当运动模糊图像的模糊长度变小时，相应地，频谱图中的条纹间距变大，条纹数量变少，此时对频谱图像进行分块得出的块图可能没有足够可用的条纹信息可供Radon 变换检测，如图3（b）所示。

图3 亮条纹和频谱分块示例Fig.3 Examples of bright stripe and spectral blocking

综上所述，现有PSF 参数估计方法在消除十字亮线和噪点、毛刺干扰时，出现了重要信息丢失和残留干扰的问题，因此，本文提出一种改进的PSF 参数估计方法，该方法的具体步骤如下：

1）获取运动模糊图像的频谱图。图4（a）所示为模糊长度L=30、模糊角度θ=120°的运动模糊图像，图像分辨率大小为720×720 像素。对图4（a）作傅立叶变换后得到其频谱图，将频谱图像动态范围压缩且居中，可以直观地观测到模糊图像的频谱条纹特征，如图4（b）所示。

2）频谱图像增强处理。为了突出条纹特征，对频谱图像进行直方均衡化（如图4（c））后再将频谱图像二值化。通过直方图均衡化拉伸像素值，增强亮暗条纹的对比度，突出条纹特征，便于后续条纹检测。然后，根据图像整体灰度值和最大类间方差法设定阈值［20］，对频谱图像进行灰度阈值转换，将灰度图像转换为二值图像，如图4（d）所示。二值图像的冗余信息更少，同时保留了必要的条纹结构，亮暗条纹的特征也更明显［21］。

图4 运动模糊图像变换过程Fig.4 Transformation process of motion-blurred image

3）形态学变换。为了消除二值图像中十字亮线以及噪点、边缘毛刺等干扰，保留形态合适的条纹图像以供参数估计检测，对二值图像进行形态学开运算，如图4（e）所示。形态学开运算可以去除比结构元素更小的明亮部分，为了控制图像开运算操作的精度以保留形态合适的中心亮条纹，需要选择合适的结构元素作形态学开运算［22］。频谱图中的亮条纹形状大致呈长方形，因此，将结构元素的形状类型定义为矩形。同时，为了保证算法的鲁棒性，根据二值化图像自适应选择合适的结构元素大小，设置程序以二值化图像中心为原点，从上、下、左、右、右上、右下、左上、左下这8 个不同方向寻找相邻的暗条纹，将找到的图像中心点与暗条纹间的最短距离作为定义结构元素大小的基准尺度。搜索相邻条纹的方式如图5 所示。

图5 相邻暗条纹搜索示意图Fig.5 Schematic diagram of searching for adjacent dark stripes

4）条纹图像边缘测定。为了避免亮条纹自身宽度导致的角度检测误差（图3（b）），对开运算后的图像进行边缘检测。具体操作是对测定图像分别进行一次膨胀和腐蚀操作，然后将膨胀后的图像与腐蚀后的图像相减，获取到的边缘图像如图4（f）所示。相比使用Canny、Soble 等微分算子对图像进行边缘检测的方法，形态学方法对边缘方向性的依赖更小，能检测出更加完整的条纹边缘。

5）运动模糊角度估算。Radon 变换是一种经典的特征提取技术，对图像作Radon 变换是在特定方向上对图像沿直线作线性积分运算，通过这种方式将包含线条的图像变换为相应的含有峰值的参数场。对条纹边缘线条图像（图4（f））进行1°～180°的Radon 变换，提取出条纹倾角φ后由式（10）计算出模糊角度θ。图4（g）和图4（h）分别为直接检测频谱和本文方法的Radon 变换结果。图4（g）中亮点面积较大，Radon 变换的角度检测结果存在较大的波动（大概在118°～122°），与直接检测的方法相比，本文方法的角度估算结果更精确。

6）运动模糊长度估算。为了降低模糊长度估算的误差，将图4（b）所示的频谱图像按估算出的角度θ顺时针旋转后作垂直投影，可得到图6 所示的频谱图像垂直投影图，此时得出的垂直投影曲线在各个峰上的峰值点分别对应频谱图像中各条纹所在位置，投影图中相邻负峰值点间的像素距离即为暗条纹间距。为了保证测算精度，根据频谱投影结果，选取投影图中与中心主峰左右相邻的2 个负峰值点间的总距离作为间距d值的估计度量（中心主峰值点距离为2d，取到的总距离为4d），求出条纹间距d后代入式（13）可得模糊长度L。

图6 频谱图像垂直投影曲线Fig.6 Spectrum image vertical projection curve

利用上述方法估算出模糊参数后，根据式（4）构造PSF，然后通过维纳滤波去卷积算法复原模糊图像。

4 实验结果及分析

4.1 PSF 参数估计实验

为了验证本文PSF 参数估计方法的有效性，将其与MOGHADDAM 等提出的经典方法［11］、胡发焕等［14］提出的改进方法进行对比实验，所有算法均使用MATLAB R2018b 编程，计算机操作系统为Windows10，CPU 为Intel Core i5-5200U 2.20 GHz，内存为8 GB。

以图4（a）为标准测试图像，该图像来源于公开图像数据集GOPRO［23］，该数据集包括真实拍摄的1 111 张模糊图像。PSF 参数估计实验的模糊参数设置参照文献［14］，将模糊尺度L设置为10 px、20 px和30 px 这3 组，模糊角度θ在0°～180°范围内每间隔15°取一个测试角度。表1 所示为3 种对比方法对同一运动模糊图像的PSF 参数估计结果。

表1 3 种方法的PSF 参数估计结果Table 1 PSF parameter estimation results of three methods

从表1 中的参数估计精确度对比结果可以看出，在不同的模糊条件下，本文方法的最大误差和平均误差均小于其他2 种估计方法。本文利用二值频谱图像条纹特征自适应地控制形态学运算精度，尽可能地消除十字亮线和冗余噪声干扰，并且通过边缘测定来避免因中心条纹自身宽度导致的角度估计误差，此外，由于本文方法未对频谱进行分块处理，在模糊长度较小时处理后的待估频谱图像中仍保留足够的条纹线条，在进行模糊长度估算时对频谱图像进行直方图均衡处理，提高了亮暗条纹的对比度，由此检测的相邻条纹间距更加准确，从而保证了模糊长度估算精度。因此，本文方法在不同大小的运动模糊图像中都能得到更精确的估计结果。

在实验中发现，在模糊长度分别为10 px、20 px、30 px 的3 组参数估计实验中，当L=10 px 时，参数估计结果的误差波动明显，且误差主要集中在模糊角度为75°、90°和105°附近。分析原因有以下2 点：1）中心十字亮线的2 条线分别呈180°和90°，当十字亮线效应严重时，残留部分会干扰相邻角度的检测结果；2）当模糊长度较小时，一些暗条纹会被中央亮条纹掩盖，从而导致对2 个相邻暗条纹间的距离估计误差变大。

图7 所示为不同PSF 参数估计方法在模糊长度为10 px时的模糊角度估计误差。从中可以看出：文献［11］方法的参数估计结果开始出现极大偏离值，参数估计结果绝度误差超过1，估计结果基本超出可信的有效范围；文献［14］方法的估计结果准确度明显优于文献［11］方法，误差波动也较小，但是在模糊角度为75°、90°和105°附近时，估计结果绝度误差仍大于0.5，影响了估计结果的可信度；本文方法在不同大小的运动模糊图像中都能得到更精确的估计结果，参数估计有效范围可达0～180°且误差更小，在参数估计误差波动明显的情况下仍能保证估计结果的可信度。总体而言，本文PSF 参数估计方法在精度和有效估计范围方面均能取得良好的性能表现。

图7 模糊长度为10 px 时的模糊角度估计误差Fig.7 Estimation error of fuzzy angle when fuzzy length is 10 px

4.2 图像复原实验

维纳滤波法是一种经典且简单高效的线性复原算法，其以原始图像和复原图像之间的均方误差最小为约束条件对原始图像进行求解。根据PSF 参数估计结果可以构造出运动模糊图像的点扩散函数，当确定了模糊图像的点扩散函数后，采用维纳滤波器可以快速复原模糊图像。维纳滤波器在对原始图像进行函数求解时表现为如下形式：

其中：e2为统计误差；E表示数学期望。

根据式（14）及图像退化模型，维纳滤波器可表示为：

其中：S为噪声功率谱与图像功率谱的比值。

图像复原结果可以直观地体现PSF 参数估计方法的准确性。为了进一步验证本文方法的可信度以及泛化性能，在测试图像中加入GOPRO 数据集中的更多图像，图像分辨率为720×720 像素，运动模糊核为随机大小。图8 所示为不同方法所构建的点扩散函数结合维纳滤波的运动模糊图像复原实验结果，为了便于描述，将图8 中的图像由上至下分别命名为“ 汽 车”“ 花 纹”“ 人 群”和“行人”。

图8 运动模糊图像复原实验结果Fig.8 Experimental results of motion-blurred image restoration

对比图8（c）、图8（d）与图8（e）可以看出，本文方法得出了更接近原始图像的清晰图像，图8（c）、图8（d）的一些复原图像中不仅没有完全消除模糊效果，且有严重的振铃效应和伪影残留，相比之下，本文方法的复原图像伪影残留更少，振铃效应更小，保留了更多的图像细节。

4.3 图像质量评价

为了客观评价复原图像的质量，本文引入峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）和结构相似性（Structural Similarity，SSIM）2 种客观评价指标。PSNR 和SSIM 的值越大，表明图像的保真度越高。PSNR 根据图像对应像素点间的误差来进行图像质量评价，定义式为：

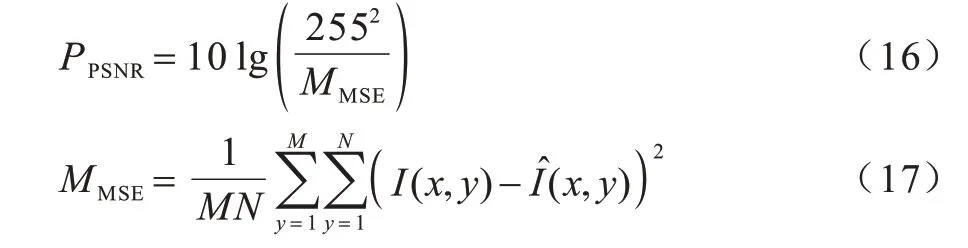
其中：MMSE表示2 幅图像间的均方误差；I(x,y)和分别是图像复原前后在像素点（x，y）处的灰度值；M、N分别为图像长度与宽度。

SSIM 从亮度（Luminance）、对比度（Contrast）和结构（Structure）三方面度量图像间的相似性，相比PSNR 等传统图像质量评价指标，SSIM 更加符合人眼对图像的视觉感知。SSIM 的取值范围为-1～1，定义式如下：

其中：I、J为输入图像；μ为图像的均值；σ为图像的标准差；σIJ为2 幅图像的协方差；C1=（K1L）2、C2=（K2L）2为常数；L为像素值的范围。本文设置K1=0.01，K2=0.03。

表2 所示为图9 中4 个不同的运动模糊图像在不同方法下的复原图像质量评价结果，从中可以看出，本文方法取得了最大的PSNR 和SSIM 值，表明在PSNR 和SSIM 客观评价指标上，本文方法结合维纳滤波复原出的图像质量最优，证明本文方法精度更高，且对不同特征、不同模糊程度的图像的PSF 参数估计结果稳定保持在可信范围内。

表2 3 种方法的复原图像质量评估结果Table 2 Evaluation results of restored image quality by three methods

5 结束语

成像时相机抖动或目标物移动等会使图像产生运动模糊，从而导致图像清晰度大幅下降。为了提高运动模糊图像PSF 参数估计结果的精度，本文提出一种改进的运动模糊参数估计方法，并利用该方法估算出的参数来复原运动模糊图像。PSF 参数估计和图像复原实验结果表明，相比文献［11，14］所提方法，该方法具有有效性且估计结果精度更高，有效估计范围更广，在相同条件下能复原出具有更少振铃和伪影的图像。在实际应用场景中，除了相机和场景之间产生线性运动造成的运动模糊外，往往还存在其他类型的模糊和噪声干扰因素，因此，下一步将寻找更合适的数学模型，以解决含有多个非线性模糊或大量噪声干扰的复杂图像复原问题。