融合安全A*算法与动态窗口法的机器人路径规划
詹京吴,黄宜庆
(1.安徽工程大学 电气工程学院,安徽 芜湖 241000;2.安徽省电气传动与控制重点实验室,安徽 芜湖 241000)
0 概述
路径规划作为移动机器人运动中的重要组成部分,是机器人完成自主导航的核心技术。根据环境和目标的不同,路径规划可分为全局路径规划和局部路径规划,应用于全局路径规划的算法有Dijkstra 算法[1]、蚁群算法[2]、粒子群算法[3]、A*[4-5]算法等,应用于局部路径规划的算法有动态窗口法(Dynamic Window Approach,DWA)[6]、人工势场法[7]等。
A*算法由HART 等[8]于1968 年提出,该算法通过启发信息指引搜索方向,搜索时间短,搜索效率高,被广泛应用于移动机器人的路径规划。但A*算法规划出的路径拐点多、不平滑,不利于机器人的运行。针对以上缺点,许多研究者对标准A*算法进行了改进。文献[9]提出将标准A*算法的搜索邻域从8 个提高到无限个,虽然解决了路径规划方向限定问题,但同时降低了搜索速度。文献[10]提出采用跳点搜索方法对A*算法进行改进,优化了算法的搜索策略,并且采用贝塞尔曲线对路径进行平滑优化,大幅提高了路径的规划效率,但算法是在全局环境已知的条件下进行扩展和搜索的,无法实现对未知障碍物的动态避障。文献[11]提出将改进的人工势场法与A*算法相结合,实现了对随机障碍物的避让,但人工势场法所规划出的路径不够平滑,不利于机器人的运行。动态窗口法结构简单,规划出来的路径较为平滑,具有良好的避障能力,但算法容易陷入局部最优,无法获得全局最优路径[12]。文献[13]提出一种改进的动态窗口法,根据激光雷达观测到的障碍物信息选取较优方位角,从而得到通过密集障碍物区的最佳路径,大幅提高了算法的运行效率。文献[14]提出的斯坦利路径跟踪方法使用A*算法进行路径规划,得到了有效的路径信息。文献[15]通过提取A*算法规划路径的关键节点定义新的评价函数,解决了标准动态窗口法易陷入“C”形障碍物且规划路径不平滑的问题。
上述文献虽然对A*算法进行了有效改进,但都忽视了机器人与障碍物之间的距离对机器人运行的影响,无法保证搜索路径的安全性。文献[16]提出一种有限损伤A*算法,该算法定义了一个损坏量,在损坏上限的范围内寻找到一条次优路径长度的安全路径。文献[17]提出一种动态生成启发式的方法,避免A*算法陷入局部极小值,大幅提高了算法的运算效率。文献[18]设计一种安全A*算法,通过加入安全距离矩阵的方法来获得一条安全的规划路径,但该算法规划出的路径转折点多,计算时间长。
本文在标准A*算法的启发函数中引入安全距离因子,以此提高路径的安全性。同时,采用平面结构法对算法规划出的路径进行优化,删除冗余节点,减少转折,并将优化后的A*算法与动态窗口法结合,实现移动机器人对未知障碍物的动态避障,获得实时避障的最优平滑路径。
1 安全A*算法
1.1 对A*算法的改进思路
A*算法是一种可根据定义的估价函数在静态环境下进行全局路径规划的启发式搜索算法,被广泛用于移动机器人的路径规划研究。该算法在尽可能保证最优路径的同时,能够大幅减少搜索时间,提高路径的搜索效率[19]。然而标准A*算法在规划从起点到终点的路径时,所得到的全局路径无法保障安全性、冗余节点多,且运动轨迹转折较多[20]。为提高路径的安全性,本文定义安全距离因子并将其引入到标准A*算法的启发式函数中,以此进行改进。
定义安全距离因子如下:
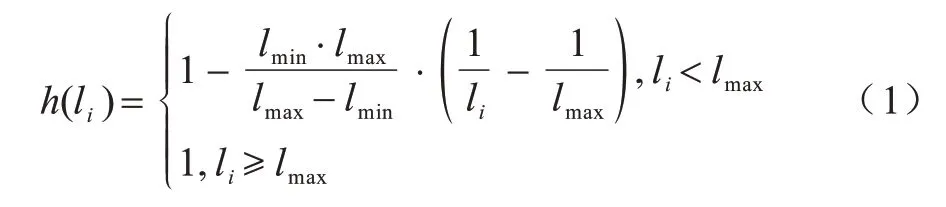
其中:lmax为移动机器人与障碍物之间接触的最大距离;lmin为机器人与障碍物之间接触的最小距离;li为机器人所在位置与障碍物之间的距离。
将安全距离因子引入标准A*算法的估价函数中,可推得:
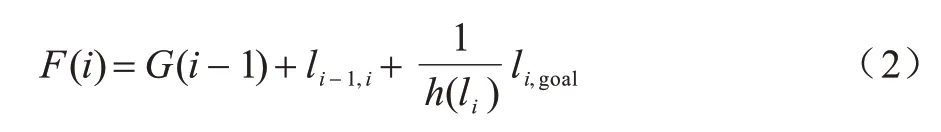
其中:F(i)为第i个节点的代价值;G(i-1)为起点到第(i-1)个节点的实际代价值;li-1,i为第(i-1)到第i个节点与障碍物之间的距离;li,goal为第i个节点到目标点与障碍物之间的距离。
1.2 基于平面结构法的路径优化
标准A*算法的路径规划是由连续的栅格中心连成的,这样很容易导致这个最优路径存在冗余节点。根据相邻节点与障碍物之间的位置关系可以判断相邻节点间是否存在障碍物,由此减少路径拐点数,实现优化路径的目的[21]。
判断路径是否有障碍物的基本原理是线段相交定理。首先需要判断点的位置关系,如图1 所示,其中,A、B、C、D 分别为平面上的任意4 个点,代表障碍物附着节点,坐标分别为(0,0)、(xb,yb)、(xc,yc)、(xd,yd)。

图1 两点位置关系判断Fig.1 Relationship judgement of two points positions
假设4 个点都在xoy平面上,则这4 个点的z轴值恒为0。μ、α、β分别代表图1 所示的向量。μ与α的向量积、μ与β的向量积分别为:

其中:m、n为向量积的系数。规定垂直纸面向外的方向为正方向,根据右手定则可知,当m、n为负数时,α在μ的顺时针方向,即C 在μ的顺时针的方向;反之,C 在μ的逆时针方向。同理,可以判断D 和β与μ的位置关系。由此可知:当m·n<0 时,C 和D 位于μ的异侧;当m·n>0 时,C 和D 位于μ的同侧。
线段相交的判定如下:在同一平面内的任意4 个点,由这4 点连接成2 条不同的线段。由上文介绍的点与线段的位置关系可以判断除该线段的两端点之外其他两点的关系,由此可确定两线段的关系。根据线段相交原理,将路径中某一节点的相邻节点连接成线段n,判断该线段上是否存在障碍物。若无障碍物则剔除;反之则保留。判断线段n与障碍物的对角线是否相交,若相交则有障碍物,该路径不变;若不相交则没有障碍物,将两节点中后一个节点剔除,如图2 所示,其中:直线路径为原始算法生成的路径;虚线路径为剔除冗余节点后的路径。
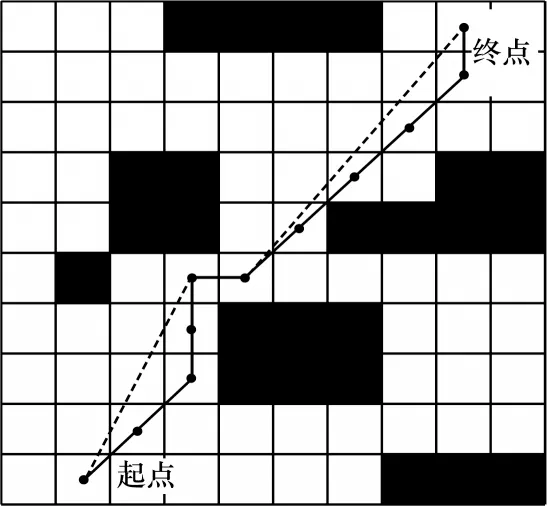
图2 剔除冗余节点示例Fig.2 Example of removing redundant nodes
基于安全A*算法的机器人路径规划流程如图3所示。

图3 基于安全A*算法的机器人路径规划流程Fig.3 Robot path planning procedure based on safety A*algorithm
2 本文融合方法
2.1 动态窗口法
动态窗口法由于具备较强的局部避障能力、灵活性强等优点,被广泛用于移动机器人的局部路径规划中。动态窗口法的基本思想是依据机器人的运动学模型和运动特征,在规划过程中对机器人的速度窗口(vt,ωt)进行约束,然后根据速度窗口,结合机器人的运动学模型进行轨迹的推演,最后利用评价函数确定最优的运动轨迹,直至到达目的地[22]。机器人的搜索空间受到机器人的运动学约束Vk、动力学约束Vb和障碍物约束Vo的限制,相关约束描述如下[23]:其中:vmin和vmax表示机器人速度的上限和下限;ωmin和ωmax表示机器人角速度的上限和下限;vc是小车的当前线速度;ωc是当前角速度;分别对应线加速度的上限和下限;分别对应角加速度的上限和下限;dmin(v,ω)表示机器人在下一时刻到障碍物的距离。
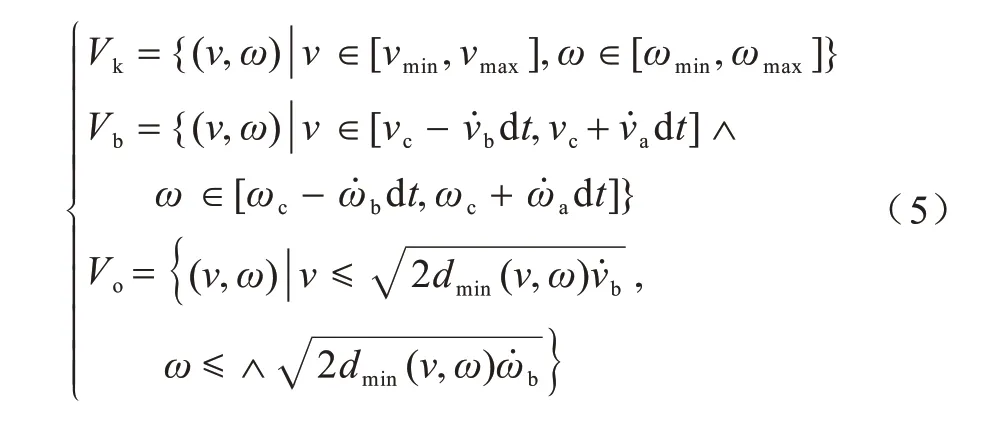
移动机器人运动学公式推导如下:
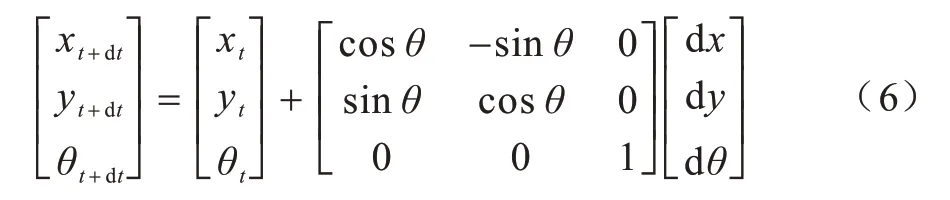
其 中:[xt+dt,yt+dt,θt+dt]T表示时刻t+dt机器人在世界坐标系中的位置;[xt,yt,θt]T表示时刻t机器人在世界坐标系中的位置;[dx,dy,dθ]T表示时刻dt机器人的位置;底盘坐标系中的理想变化量[dx,dy,dθ]T=[vxdt,vydt,ωdt]T;vx和vy为机器人在底盘坐标系中沿x轴和y轴的线速度;ω表示移动机器人的角速度。
在计算多组采样速度的轨迹后,应用评估函数进行评分并选择最佳组[24]。评估函数描述如下:
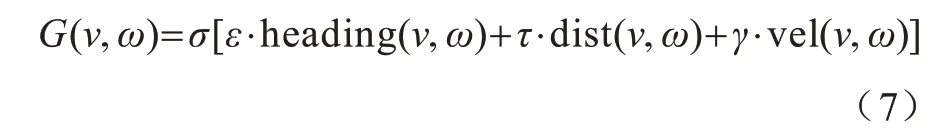
其中:heading(v,ω)用于测量朝向目标的进度,当机器人直接移动到目标时,该进度最大;dist(v,ω)表示到静态障碍物的最近距离;vel(v,ω)表示前进速度;ε、τ、γ是权重;σ是3个评价函数的归一化参数。
2.2 融合安全A*算法与DWA 的路径规划方法
通过设计路径融合子函数fusion(v,ω),扩展原始动态窗口法的评价函数,计算公式如下:

其中:(x1,y1)为动态窗口法基于采样轨迹而推演出的局部路径末端坐标;(x2,y2)为安全A*算法获得的全局路径节点坐标。
为了与安全A*算法相结合,同时考虑导航方法的实时性,根据上文推导,更新动态窗口法的评价函数如下:

其中:κ为权重。
通过采用更新后的评价函数,可以在全局地图中获取考虑实时避障的最优平滑路径。基于融合方法的机器人动态避障流程如图4 所示。
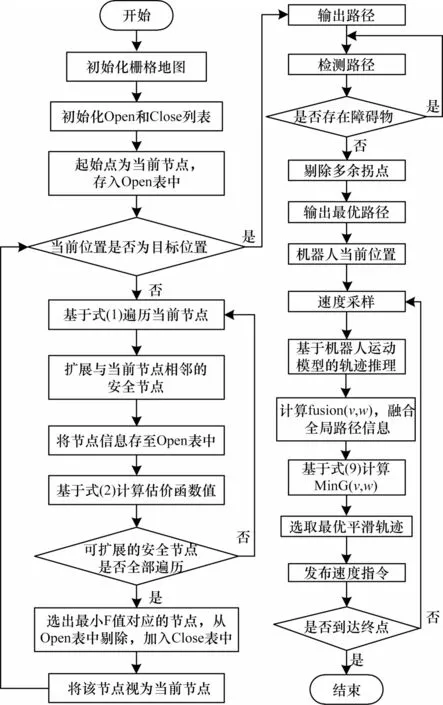
图4 基于融合方法的机器人动态避障流程Fig.4 Robot dynamic obstacle avoidance procedure based on fusion method
3 仿真验证与实物验证
3.1 仿真验证及分析
3.1.1 安全A*算法验证
在Intel®CoreTMi5-10300H CPU @ 2.50 GHz 的Matlab 仿真平台上验证本文融合方法的有效性和可行性。首先依据上文环境模型的搭建基础,设置20 m×20 m和30 m×30 m 的栅格地图。使用文献[25]提出的改进A*算法、本文提出的安全A*算法、标准A*算法以及Dijkstra 算法进行多组仿真对比实验。仿真结果如图5和图6 所示,性能指标如表1 和表2 所示。可以看出:在简单环境下,本文算法较文献[25]算法减少5.2%的路径长度和5 个转折点,缩短近43%的搜索时间;在复杂环境下,由于环境的复杂程度不相同,本文算法的路径长度和搜索时间较文献[25]算法有较大提升;4 种算法得到的转折点相差不大,由于需要获得安全的路径,因此本文算法较标准A*算法会牺牲一定的距离代价,但每个路径节点到最近障碍物的平均距离有所增加,增强了路径的安全性。

表1 简单环境下的路径规划性能对比Table 1 Comparison of path planning performance under simple environment

表2 复杂环境下的路径规划性能对比Table 2 Comparison of path planning performance under complex environment
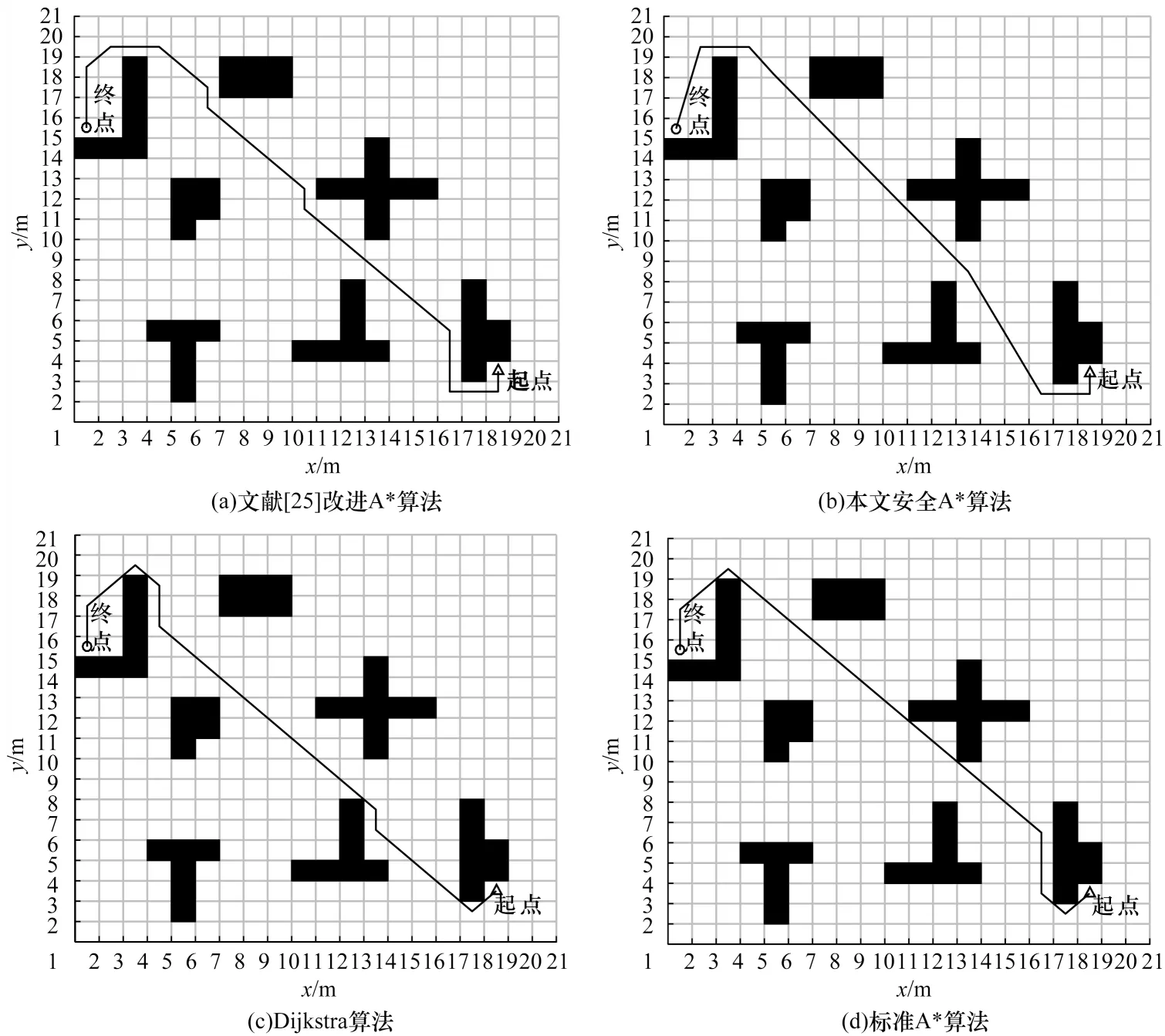
图5 简单环境下的路径仿真结果对比Fig.5 Comparison of path simulation results under simple environment

图6 复杂环境下的路径仿真结果对比Fig.6 Comparison of path simulation results under complex environment
3.1.2 融合方法性能验证及灵敏度分析
依据上文简单环境的配置,设置融合方法规划的参数。根据文献[21]中的权值设置,通过多组仿真数据对比,选择各个参数值为:ε=0.15,τ=0.25,γ=0.25,β=0.35。通过在环境中设置突然出现的障碍物,可以有效验证融合方法的避障性能。对融合方法的验证结果如图7 所示。从图7(a)中可以看出,当地图中没有随机障碍物时,安全A*算法和安全A*融合动态窗口法都能规划出一条从起始点到终点的路径。当加入一个随机障碍物时,如图7(b)所示,显然安全A*算法无法规避随机加入的障碍物,而安全A*融合动态窗口法能有效识别随机障碍物并进行动态避障。随着障碍物的增加,如图7(c)、图7(d)所示,融合方法都能有效避开环境中加入的随机障碍物,同时准确追踪基于安全A*算法生成的全局路径,从而验证了本文融合方法的有效性和可靠性。
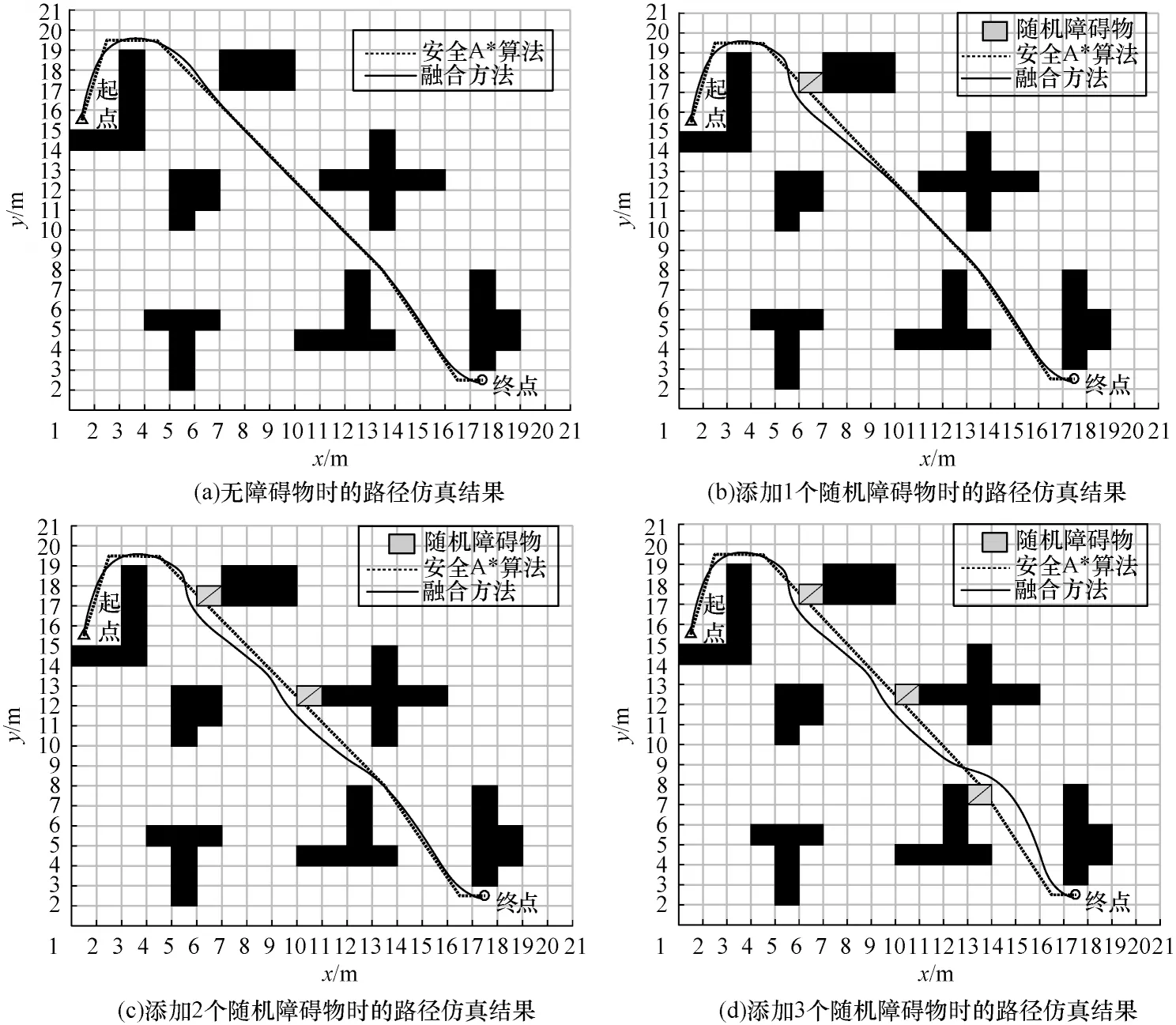
图7 随机障碍物避障路径仿真结果Fig.7 Simulation results of random obstacle avoidance paths
路径长度和时间随加入障碍物个数的变化如图8 所示,可以看出,随着障碍物的增加,融合方法规划出的路径长度和规划时间呈线性增加。机器人控制参数反馈如图9 所示。

图8 路径长度和时间随障碍物个数的变化Fig.8 Variation of path length and time with the number of obstacles
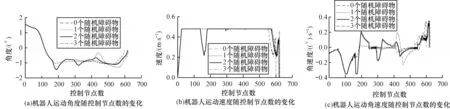
图9 机器人角度、速度、角速度输出结果Fig.9 Output results of robot angle,velocity and angular velocity
3.2 实物验证及分析
借助自主搭建的机器人平台对本文提出的融合方法进行验证,如图10 所示。

图10 机器人验证平台和地图环境Fig.10 Robot verification platform and map environment
机器人参数设置如下:RIKIBOT-四驱-主控-工控机-stm32 驱动板-思岚A1 雷达组装。
在实验过程中,通过在环境中设置障碍物,验证本文融合方法的有效性。首先机器人在静止环境中进行导航,当机器人回到起点时,随机改变障碍物的位置,验证导航算法在动态环境中的导航性能。机器人导航过程如图11 所示,可以看出,机器人在执行一个来回的任务时,虽然环境中的障碍物位置发生改变,但是机器人仍然可以安全抵达位置。输出的机器人参数如图12 所示,结果表明,本文融合方法具备实时避障的能力,且能安全地抵达目的地。

图11 机器人导航过程Fig.11 Process of robot navigation
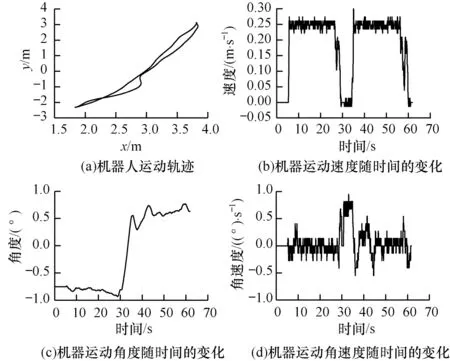
图12 机器人状态输出Fig.12 Robot state output
4 结束语
针对标准A*算法规划路径冗余点多、安全性低以及无法在复杂环境下随机避障的缺点,本文提出一种融合安全A*算法和动态窗口法的方法,充分利用两种算法的优势。与标准A*算法、文献[25]改进A*算法和Dijkstra 算法的仿真对比结果表明,本文融合方法实现了路径长度、运算效率、平滑性以及安全性的优化。在机器人平台上的实验结果也表明,本文融合方法能高效地完成实际环境中的路径规划任务,实现对随机障碍物的有效避障。由于本文只研究了对于静态未知障碍物的实时避障,未考虑到动态障碍物,因此下一步将会对动态窗口法进行改进,并在现有环境中加入动态障碍物,使本文融合方法在各种复杂环境中均能得到最优路径。

