基于曲率相似性的路面连续纵长裂缝匹配方法*

陈实 黄玉春

（武汉大学遥感信息工程学院 武汉 430079）

0 引言

由于车辆挤压和雨水侵蚀的作用，我国公路路面上出现裂缝等病害的状况日益严重。国内研发了车载路面状况检测系统，如南京理工大学研发的N-1系统、武汉大学研发的ZOYON-RTM系统、交通部公路科学研究院研发CiCS系统和长安大学研发的CT-501A系统[1]等。通过专业车辆采集道路图像存在运行成本高、设备维护昂贵和使用不灵活等缺点。随着传感器技术和图像处理技术的快速发展，越来越多的传感器被用来采集道路数据，如今通过在车辆上安装手机、平板等轻便设备，在车辆行驶的同时采集前方道路倾斜图像。由于道路上存在许多过长的纵向裂缝，以这种方式采集图像，每张图像只能拍摄到纵缝的一部分，1条裂缝被错误当作多条裂缝，从而产生错误计算裂缝的长度、重复记录裂缝信息等问题。

连续拍摄的图像中相邻2张图像的裂缝间存在较大的重叠度，因此可以从每张图像中提取裂缝曲线并将其匹配连接成1条完整的裂缝曲线。本文将基于此目标展开问题的研究。目前，国内外已经有许多学者对曲线匹配问题展开研究。Wolfson[2]解决了欧式变换下的曲线部分与部分匹配问题。Kong等[3]提出的算法能够解决曲线部分与部分匹配的问题，但该算法不允许2条曲线之间进行过均匀缩放。Cui等[4]对开放的二维曲线匹配问题提出了有效方法，该方法能解决相似变换下曲线部分与部分匹配问题。Petrakis等[5]和Mai等[6]提出了在曲线局部缺失情况下的匹配方法。目前对于曲线匹配的研究都只停留在能够解决无透视形变的曲线匹配问题。但道路上纵长裂缝在倾斜拍摄过程中肯定会发生透视形变，使用上述方法很难解决裂缝匹配问题。道路上的裂缝形状随意，所以倾斜图像中裂缝匹配问题比一般情况下二维曲线的匹配更加困难。国内外有许多学者以特征点匹配的方式实现路面裂缝图像匹配，先使用Harris、FAST[7]等方法提取特征点，然后使用RANSAC算法对存在匹配错误的特征点进行剔除[8]，根据匹配的特征点完成图像拼接，常见的有SIFT[9]、SURF[10-11]等算法。吕岩等[12]提出了基于图像局部特征描述算子对路面裂缝匹配及拼接。朱力强等[13]利用裂缝角点的特征点集，提出了基于距离的裂缝图像匹配算法。Morel等[14]对SIFT算法进行改进，提出ASIFT算法来弥补SIFT算法在倾斜图像中只能提取到很少的特征点的缺点。因ORB（oriented FAST and rotated BRIEF）具有速度快、表征能力强的特点[15]，李超峰[16]使用SIFT算法作为特征点检测算法，以ORB中特征点描述替代SIFT算法的特征点描述的方式加快SIFT算法处理速度，实现路面裂缝图像匹配[17]。特征点匹配没有考虑路面裂缝空间位置分布特征，大量的特征点都参与匹配，造成算法速度较慢。由于光照不均匀和路面噪声干扰，一些关键的特征点容易被剔除，导致裂缝匹配错误。为了解决这些问题，本文先使用逆透视变换去除倾斜图像中裂缝存在的透视形变，然后考虑了路面裂缝空间位置分布特征并基于曲率相似性提出了1种由粗到精的2阶段纵长裂缝匹配的方法。

1 基于逆透视变换的裂缝曲线提取

1.1 逆透视变换

道路上的裂缝在相机小孔成像过程中，经过了透视形变，图形间的相对位置关系发生较大改变，因此倾斜图像中裂缝曲线匹配难度大。如果将问题分解，先进行逆透视变换，将倾斜图像还原成正射图像，剩下的就是相似变换下的曲线匹配问题。见图1，以相机光心为原点，车辆前进的方向为Yw轴，垂直于Yw轴的方向为Xw轴，垂直于路面向上的方向为Zw轴，建立世界坐标系Xw-Yw-Zw，Xc-Yc-Zc表示相机坐标系，见式（1），在已知相机内参f、dx、dy和外参θ、h的情况下，将px坐标系转成相机坐标系，再由相机坐标系转成世界坐标系，得到世界坐标点与px坐标点一一对应关系，用一定采样间隔对图像重采样得到分辨率一致的正射图像。

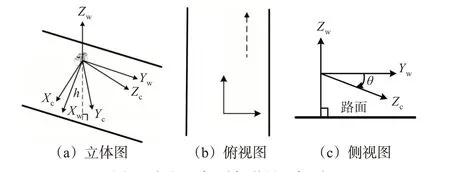
图1 相机坐标系与世界坐标系Fig.1 Camera coordinate system and world coordinate system

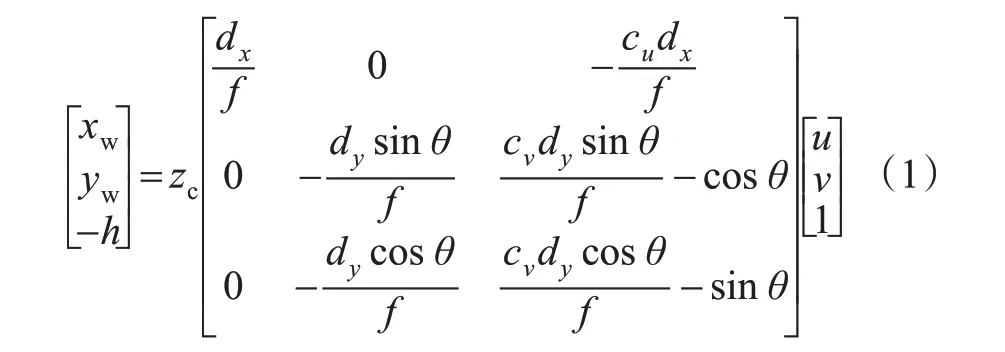
式中：(xw，yw，-h)为世界坐标点，mm；(u，v，1)为px坐标点，px；h为相机相对于路面的高度，mm；f为相机焦距，mm；dx，dy分别为单位px对应于图像平面坐标系x轴和y轴的长度，mm；θ为俯仰角（Zc轴在Yw-Zw平面内的投影与Yw轴的夹角），rad。

1.2 裂缝曲线提取

正射图像中的裂缝曲线提取目的是分割出裂缝图像中的裂缝px。常见的道路裂缝图像分割算法有基于阈值的分割算法[18]、基于边缘检测的分割算法[19-20]和基于种子生长的图像分割算法[21]等。道路图像的采集工作都是在户外进行，所以在图像的采集过程中极易受外界环境的干扰，如光照强度变化或者路面噪声干扰等[22]。阈值分割算法适合光照均匀、对比度高的图像；当图像的噪声较多时，边缘检测算法的效果较差；基于种子生长的算法需要初始种子点。以上3种算法应用到道路图像上都存在局限性，深度学习的方法显示出比传统图像处理方法更好的性能。因此采用深度学习中的语义分割网络Deeplab V3+提取出裂缝px。网络训练集使用的是G45裂缝数据集，该数据集由专业车辆在武汉G45国道采集，共569幅灰度图像，每张图像的分辨率为512×512。采用联通域标记方法，将裂缝px标记成不同的区域然后删除面积小于阈值的联通区域，从而去除网络输出图像中的噪声点。提取出裂缝的骨架，生成连续曲线。经过逆透视变换和裂缝曲线提取之后，得到了裂缝曲线中各点的px坐标，接下来进行裂缝曲线的匹配。

2 裂缝曲线特征描述

曲线匹配的关键是如何获得稳定并且准确的曲线特征，该特征要能够很好地表示曲线形状。见图2，曲线在每个点上的曲率反映了曲线在该点的局部形状与走势。因此本文从曲线的曲率出发，对曲线的特征进行提取。

图2 曲线曲率特征Fig.2 Curvature characteristics of curve

使用一维高斯函数平滑曲线，去除噪声并保留曲线局部较大的曲率，然后等弧长间隔（采样长度）对平滑后的曲线进行重采样。重采样方法见图3，原曲线由一系列首尾相连的线段组成，以采样长度为间隔分割线段得到采样点，直至剩余长度小于采样长度，将剩余长度加入下1个线段，并开始在下1个线段上添加更多的采样点，直到遍历完原曲线。计算每个采样点的曲率，见式（2）。

式中：κ为曲率；x'和y'分别为曲线在x轴和y轴方向上的一阶导数；x''和y''分别为曲线在x轴和y轴方向上的二阶导数。曲线采样点的曲率集合称为曲线描述符{κ}。

3 裂缝曲线粗匹配

裂缝曲线经过逆透视变换后，各点的相对位置保持不变，曲率特征具有相似性。通过分析曲率的相似性，进行裂缝曲线的匹配。利用曲线特征对不同的曲线进行比较，找到不同曲线部分中相似或相同的部分，即是曲线相匹配的部分。相邻的2张图像中前1张图像拍摄到完整的裂缝，后1张图像拍摄到裂缝部分，这种情况属于裂缝整体与部分的匹配，见图4（a）中绿色部分。车载相机在拍摄路面的过程中，单次拍摄只能拍摄到过长裂缝的一部分，过长的裂缝会同时存在于相邻2张或多张图像中，应该依据相邻图像中裂缝曲线的相同或相似部分将其匹配连接成完整的裂缝，这种情况属于裂缝部分与部分的匹配，见图4（b）中绿色部分。裂缝部分与部分匹配是裂缝整体与部分匹配的一般情况，本文在裂缝整体与部分匹配的基础上进行裂缝部分与部分匹配。

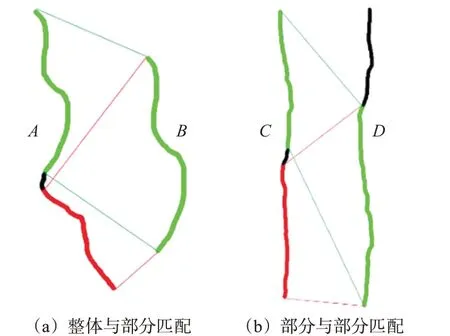
图4 曲线匹配示意图Fig.4 Diagram of curve matching

3.1 裂缝曲线距离度量

2个匹配的曲线具有相似的描述符，不匹配的描述符相差很大。给定曲线Si的描述符Di={|p=1，2，…，N}和曲线Sj的描述符Dj={|p=1，2，…，N}，定义距离v度量方法见式（3）。

式中：为Si第p个点的曲率；为Sj第p个点的曲率。

基于曲线特征描述符，使用距离度量评判2段曲线的邻近程度。

3.2 裂缝曲线整体与部分的匹配

如图4（a）所示，2段曲线A和B，曲线A的绿色部分与曲线B有相似的描述符，曲线A的红色部分描述符与曲线B的相差很大。

曲线A={ai|i=1，2，…，N}，曲线B={bi|i=1，2，…，M}，ai和bi分别表示曲线A和B的第i个点。曲线整体与部分的匹配问题中，主要任务是找到曲线B在曲线A中的起始和终止位置。

以等间隔长度l0分割曲线，得到n个分割点，任意2个分割点之间的子曲线作为待匹配子曲线，曲线A包含待匹配子曲线数等于，C为组合符号。将A的所有子曲线重采样成M（B采样点的个数）个点，计算子曲线采样点的曲率，得到子曲线描述符。A的子曲线序列S={Ai|i=1，2，…，}，其中Ai表示第i个子曲线，给定子曲线Ai的描述符Di={κp|p=1，2，…，m}，κp为子曲线Ai第p个点的曲率，描述符有m维。描述符序列T={Di|i=1，2，…，}，B的曲线描述符D={κp|p=1，2，…，m}，κp为曲线B第p个点的曲率。

在裂缝曲线很长的情况下，子曲线序列S中曲线个数很多，一一进行匹配，算法复杂度很大。利用K-d tree可以很大程度上减小搜索范围，有效提高算法的效率。本文基于K-d tree最邻近算法，找出与整条曲线B匹配程度最高的Ai。计算描述符序列T中每一维上曲率值的方差，方差越大说明曲率在该维上的分布越分散，选取方差最大的一维记为X(1)，X(1)维中曲率值的中位数作为划分点，包含该划分点的曲线描述符作为根节点，左子节点中曲线描述符X(1)维的值小于划分点，右子节点中曲线描述符X(1)维的值大于划分点。对于深度为o的节点，选择方差第o大的维度作为X(o)，重复以上过程，直至不能再划分为止，不可划分的曲线描述符放入叶子节点，建成K-d tree。

基于K-d tree最邻近裂缝曲线粗匹配算法见图5，对于待匹配的曲线描述符D，首先从根节点出发按照每层节点划分规则进行搜索直至叶子节点；计算D与叶子节点的距离vmin；返回到叶子节点的父节点，判断当前描述符与D的距离是否大于vmin，如果小于则更新vmin并在当前节点的另1个子节点寻找是否有更邻近的描述符，如果大于则回退到当前节点的父节点，不断搜索与D更邻近的描述符并更新vmin，直至回溯到根节点，算法结束，得到匹配结果。

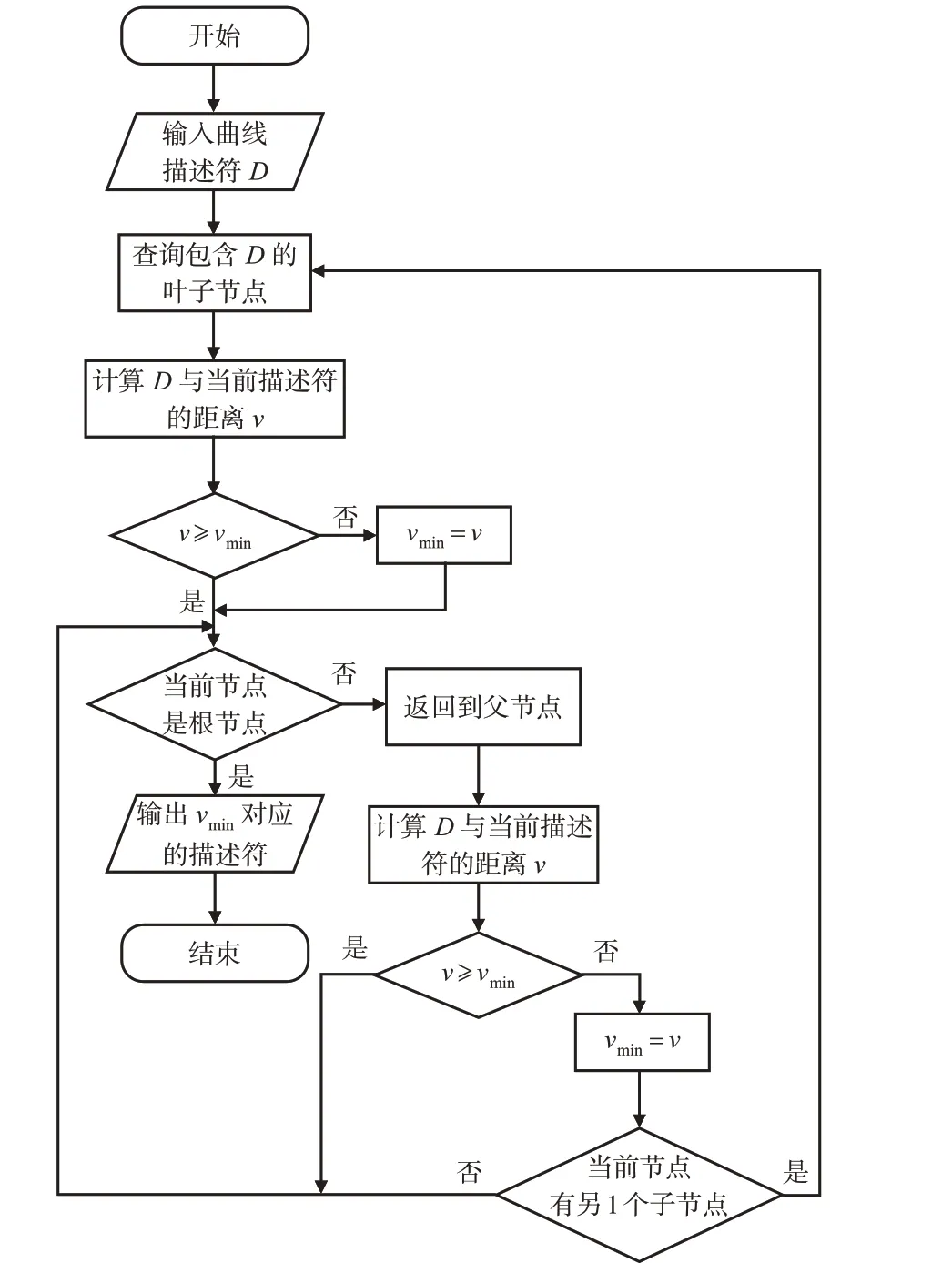
图5 基于K-d tree最邻近裂缝曲线粗匹配算法Fig.5 CrackcurvenearestmatchingalgorithmbasedonK-dtree

3.3 裂缝曲线部分与部分的匹配

由图4（b）可见：2段曲线C和D，曲线C绿色部分与曲线D绿色部分有相似的描述符，曲线C红色部分与曲线D绿色部分的描述符相差很大。

在裂缝曲线整体与部分的匹配算法基础上进行裂缝部分与部分匹配。将C和D分别以等间隔长度l0和l1分割曲线，得到n个分割点，任意2个分割点之间的子曲线作为待匹配子曲线，C的待匹配子曲线，依次使用裂缝曲线整体与部分的匹配算法，找到与其匹配的部分，记录vmin。曲线C待匹配子曲线都完成匹配后，在所有vmin中找最小值Vmin。根据Vmin查询对应的子曲线对(ci，dj)就是匹配结果。

3.4 连续拍摄图像中裂缝曲线匹配的改进

由于某些裂缝曲线的特征不明显，很可能导致匹配结果出现错误。车载相机采集数据过程中，相机先拍摄1张图像，车辆向前移动一段距离后，相机再拍摄下1张图像，相邻2张图像中后1张图像的裂缝是前1张图像的裂缝的延伸。前1张图像中裂缝曲线的头部与后1张图像中裂缝曲线的尾部应该是匹配的。

根据此实际场景，改进裂缝曲线匹配方法。相邻2张图像，前1张图像中裂缝曲线记为f，后1张图像中裂缝曲线记为h。曲线的2个端点从上到下的顺序分别称为起点和终点。分割曲线时，限定f的子曲线起始位置都是f的起点，限定h的子曲线终止位置都是h的终点。这样处理后大大减少待匹配子曲线的数量并且可以减少由于裂缝曲线特征不明显造成匹配结果错误的发生。粗匹配结果记为子曲线对(fi，hj)。

4 裂缝曲线精调整

因以一定间隔分割曲线的方式不能获得曲线的所有潜在的子曲线，最优的匹配结果有可能不在待匹配的子曲线序列，分割间隔越大，粗匹配结果误差越大。因为添加了限定条件，粗匹配结果(fi，hj)中只有hj起始位置和fi终止位置存在误差。在粗匹配结果的基础上，分别在hj起始位置和fi终止位置的误差范围内迭代调整。以精调整hj起始位置为例，fi的终止位置可以采用相同的方法进行精调整。

曲线hj的描述符D={Xp|p=1，2，…，m}，Xp为第p个点的曲率。曲线fi的描述符D={Yp|p=1，2，…，m}，Yp为fi第p个点的曲率。

基于曲线特征描述符，用归一化互相关系数（normalized cross correlation，NCC）来描述2段曲线之间的相关程度。计算2段线之间的归一化互相关系数，见式（4）

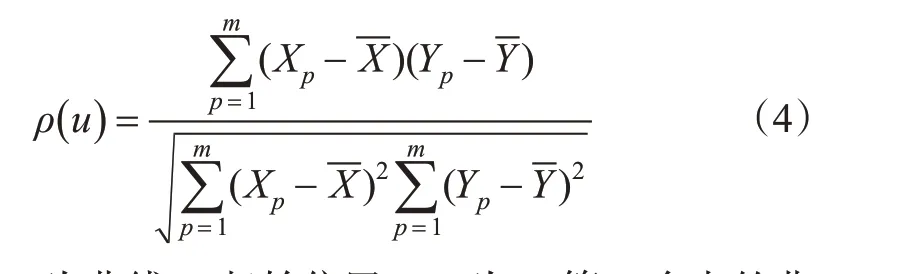
式中：u为曲线hj起始位置；Xp为hj第p个点的曲率；Yp为fi第p个点的曲率；为曲线hj描述符的平均值；-Y为曲线fi描述符的平均值；ρ(u)为曲线hj起始位置为u时与曲线fi的归一化互相关系数。ρ取值范围是[-1,1]，在实际裂缝曲线匹配过程中只考虑正相关，即ρ的值越大，裂缝曲线的相关程度就越高。

步骤1。计算起始位置为u时hj的描述符和fi描述符的ρ(u)。

步骤2。hj起始位置在[-l+u，l+u]范围内以l/r为间隔取值，值记为k，l初始值是粗匹配时分割间隔，r是缩小系数，依次计算不同起始位置时hj与fi描述符的ρ(k)，如果ρ(k)增大则更新ρ(u)和hj起始位置u。

步骤3。分割间隔从l更新成l/r。

步骤4。当hj与fi描述符的ρ≥阈值或者迭代次数超出最大次数时，输出hj的起始位置u，结束算法，否则回到步骤2。

图6为精调整hj起始位置的过程。

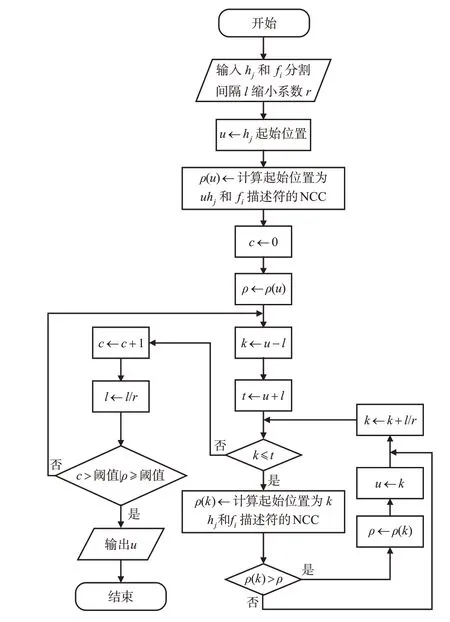
图6 精调整起始位置流程Fig.6 Process of fine adjust starting position

5 实验验证

5.1 实验对象

武汉大学校园内道路众多，路面破损情况复杂，许多道路上出现严重程度不等的裂缝。因此，笔者选取武汉大学校园内10个路段作为实验数据采集地点。通过车载相机采集道路前方倾斜图像，每个路段中选取连续拍摄的道路图像作为1组实验数据。

5.2 实验误差评定

在确定了2条裂缝匹配部分的起始和终止位置后，根据匹配点计算出2条裂缝之间相似变换矩阵，见式（5），二维图像中相似变换的变换矩阵共4个自由度。

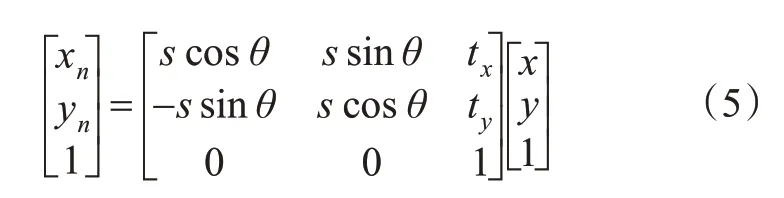
式中：x和y分别为匹配点在x轴和y轴方向上的坐标；xn和yn分别为匹配点相似变换后在x轴和y轴方向上的坐标；tx和ty分别为x轴和y轴上平移量，px；θ为旋转角，rad；s为缩放因子。当匹配部分包含至少3个匹配点时，每点有x和y这2个坐标可以列出2个线性方程，所以至少得到6个线性方程，采用最小二乘法或者SVD分解足以求解出4个未知量。f相似变换后得到曲线g，见式（6），计算g与h的均方根误差（root mean squared error，RMSE）R，R越小则匹配结果越好，R越大则匹配结果越差。

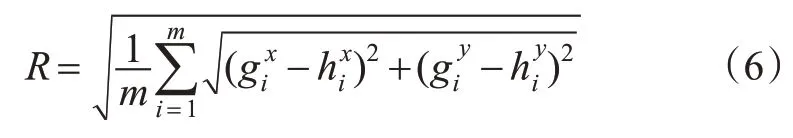
式中：和分别为曲线g第i个点的x坐标和y坐标，px；和分别为曲线h第i个点的x坐标和y坐标，px。

5.3 实验结果及分析

为了验证该方法的有效性，在每组实验中，先对原始图像进行逆透视变换，提取出裂缝曲线f和h，然后进行裂缝粗匹配和精调整，分别计算粗匹配和精调整得到裂缝匹配结果的RMSE。粗匹配与精调整裂缝匹配误差对比见图7，实验误差均小于1.3 px，其中有6组实验误差小于1 px，第5组实验误差最小。对比粗匹配和精调整，精调整后RMSE平均减小了24.19%，证明该方法优化匹配结果的有效性。在粗匹配效果较差的情况下，精调整也能明显优化匹配结果。

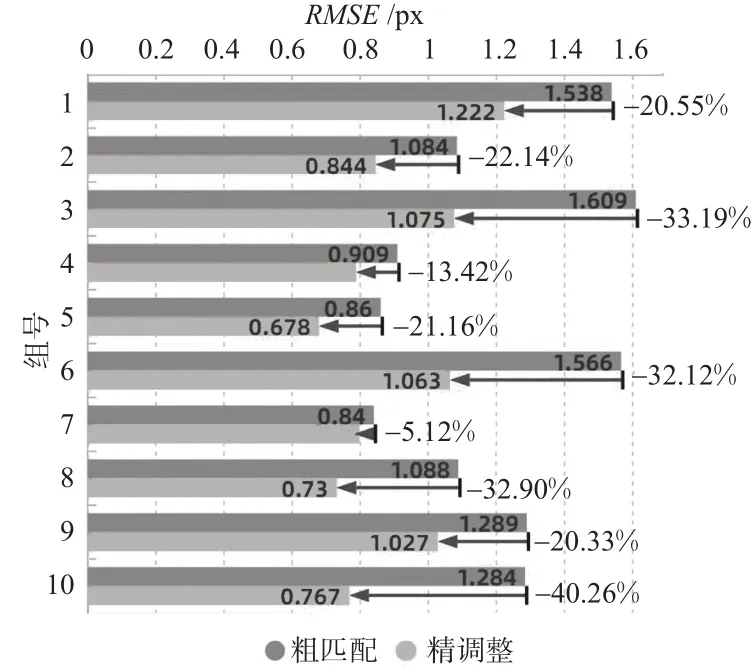
图7 粗匹配与精调整裂缝匹配误差Fig.7 Matching error of coarse matching and fine adjustment

简单裂缝实验结果见图8。图8(a)和图8(e)是连续拍摄的2张原始图像，图8(b)和图8(f)是2张原始图像分别经过逆透视变换后得到的正射图像，图8(c)和图8(g)分别是图8(b)和图8(f)中矩形框区域内的图像，图8(d)和图8(h)是分别从图8(c)和图8(g)中提取的2条曲线，绿色表示2条曲线匹配的部分，红色曲线是曲线h经过相似变换之后得到的曲线。粗匹配结果的RMSE等于1.538 px，精调整结果的RMSE等于1.222 px，精调整后RMSE减小了20.55%。对比图8（e）和图8（f），精调整后2条曲线匹配部分更准确，2条曲线拼接后的重合程度更高。图8（g）是曲线f和曲线h连接并融合成1条完整的曲线。对于分叉的复杂裂缝，将其分为多条简单裂缝，依次进行本文匹配方法，找到简单裂缝间最佳匹配部分。复杂裂缝实验结果见图9。粗匹配结果的RMSE等于1.297 px，精调整结果的RMSE等于0.901 px，精调整后RMSE减小了30.53%。

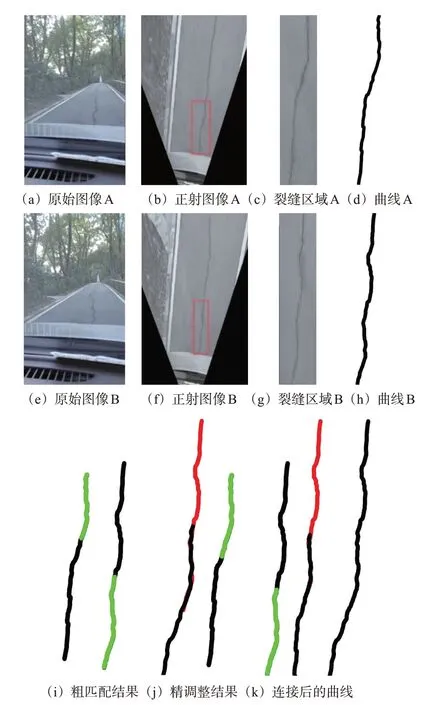
图8 简单裂缝实验结果Fig.8 Results of simple crack

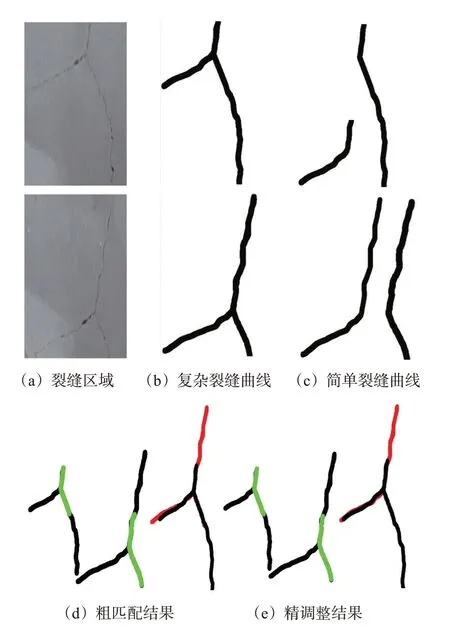
图9 复杂裂缝实验结果Fig.9 Results of complex crack

为了进一步验证方法的鲁棒性，进行多次仿真实验。通过向曲线h添加期望值为0，标准差不同的高斯噪声来模拟真实环境下的各种干扰，分11组使用本文提出的方法对含噪声的曲线进行匹配实验，每组实验重复进行50次并对误差结果取平均值，最终仿真实验误差结果见图10。随着高斯噪声的标准差从0增大到2 px，匹配误差仅增大1.083 px，结果表明方法抗噪声能力较强。第11组仿真实验的曲线匹配结果见图11，匹配结果的RMSE等于1.87 px，图11（d）中2条曲线匹配部分有较高的重合度。经过以上实验证明，该方法能够很好地解决连续纵长裂缝匹配问题。

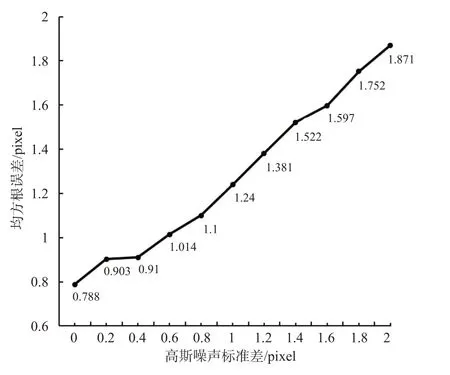
图10 仿真实验曲线匹配误差Fig.10 Error of curve matching in simulation experiment

图11 仿真实验结果Fig.11 Results of simulation experimen

使用SIFT算法对原始图像裂缝区域进行匹配和本文方法进行对比。SIFT算法的平均误差等于3.195 px，本文方法的平均误差等于0.899 px，本文方法的平均误差与SIFT算法相比减小了71.86%。使用本文方法在10组实验中都能匹配成功，使用SIFT算法在其中2组实验中得到完全错误的匹配结果。当特征点匹配正确时，见图12（a），SIFT算法的误差等于0.599 px，本文方法的误差等于0.767 px，绿色是提取的特征点，粉红实线连接相匹配的特征点，右侧是2张裂缝图像融合后的结果，SIFT算法共检测出6对匹配点，其中6对正确匹配点。当存在较多错误匹配点时，见图12（b），SIFT算法的误差等于12.978 px，本文方法的误差等于0.730 px，SIFT共检测出10对匹配点，其中3对正确匹配点，7对错误匹配点，拼接成的裂缝完全错误。根据错误匹配结果拼接成的图像发生拉伸形变，并且影响裂缝px的提取，对后续裂缝长度和宽度的计算造成很大误差。

图12 SIFT算法匹配结果Fig.12 Matching results of SIFT algorithm

6 结束语

笔者针对道路裂缝检测工作中出现的实际问题，提出倾斜图像中连续纵长裂缝匹配的方法，该方法解决了由于相机视场角有限每次只能拍摄到道路上纵长裂缝的一部分问题。在基于K-d tree最邻近匹配算法对裂缝曲线进行粗匹配的后，考虑了车载相机采集道路图像的特点和分割曲线方式的局限性，改进了算法，降低了匹配结果的误差，实现了针对纵长裂缝的匹配结果精细化调整。能够检测出完整并且准确的裂缝曲线，不仅是计算裂缝的长度、宽度的重要基础，而且还可以避免裂缝数量的错误估计和裂缝信息的冗余记录，对道路裂缝检测和道路养护工作的进行有着重大帮助。

本文研究的是校园内道路，道路状况较为简单，对于多车道公路、有其他裂缝干扰等复杂情况，还未展开研究。后续将进一步研究复杂道路情况下的纵长裂缝匹配方法。