障碍空间中Voronoi图优化的反向近邻数聚类算法

何云斌，刘婉旭，万 静

哈尔滨理工大学 计算机科学与技术学院，哈尔滨 150080

聚类在统计数据分析、图像处理、模式识别等领域的应用十分广泛，是一种常用的无监督分析方法。它根据数据样本的相似程度将样本划分为若干个簇，其目的是使得同一个簇中的样本相似性大，不同簇间的样本相似性小。现有的聚类算法以所采用的基本思想为依据将它们分为五类，即基于划分的聚类、基于层次的聚类、基于网格的聚类、基于模型的聚类以及基于密度的聚类方法。

选址问题在物流、生产和生活方面有着广泛的应用，比如物流中心、垃圾厂、ATM 机的放置等。随着互联网的发展，越来越多的人选择在网上购物，物流发展迅速，物流中心选址的好坏直接影响到服务质量和成本，合适的选址会给人们生活带来便利。由于在现实世界中存在河流、山川等许多障碍，障碍物的存在增加了选址问题的困难。

事实上聚类的结果会受到障碍的影响。例如图1中，当空间中不存在障碍物时，很明显聚类簇数为2。而在图2 中，由于障碍的存在，将原有的两个聚类分成了4 个聚类。因此，障碍的存在会影响聚类结果。

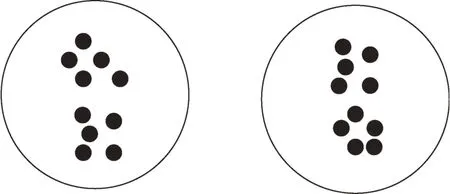
图1 空间中不存在障碍物时的聚类结果Fig.1 Clustering results in absence of obstacles in space

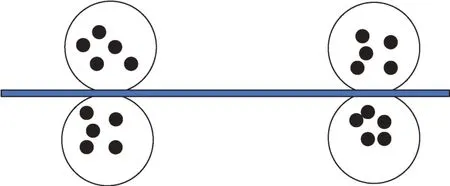
图2 空间中存在障碍物时的聚类结果Fig.2 Clustering results in presence of obstacles in space

近年来，随着障碍空间中的聚类算法在互联网上不断出现，障碍聚类算法的研究越来越受到人们的重视。文献[10]首次提出了障碍空间中的聚类问题，并给出了一个带障碍的聚类算法CODCLARANS（clustering with obstructed distance clustering algorithm based on randomized search），该算法能有效地实现带障碍的聚类，但需占用大量的内存资源，障碍的数量和形状对算法的执行时间影响较大。因此文献[11]提出了一种基于网格的带障碍的聚类算法DCellO，该算法以网格为基础，将基于密度的聚类算法与图形学中的种子填充着色算法相结合，削减了计算量，能够在有障碍存在的情况下进行任意形状的带障碍的聚类并能更好地处理噪声点。Voronoi 图是由图中各个相邻点连线的中垂线组成的连续多边形组成的，其临近特性在解决计算机几何领域的相关问题时发挥着重要作用。曹科研等人在文献[12]中提出了一种障碍空间中的不确定数据聚类算法OBS-UK-means（obstacle uncertain K-means），并在此算法的基础上运用R 树、Voronoi 图两种剪枝方法和最短距离区域的概念相结合，减少了计算量，聚类结果与单纯考虑障碍约束算法相比执行效率更好，实用价值更高。万静等人引入计算几何中的Voronoi 图对数据空间进行划分，提出障碍空间中基于Voronoi 图的不确定数据聚类算法。该算法根据Voronoi 图的性质，利用KL 距离进行相似性度量，根据障碍集合是否发生变化，分别提出静态障碍环境下和动态障碍环境下的不确定数据聚类算法。文献[14]提出了一种基于约束的密度聚类算法，该算法将障碍物建模作为预处理步骤，结合DBSCAN（densitybased spatial clustering of applications with noise）算法，能够检测任意形状和大小的聚类，对噪声和输入次序不敏感。这些算法虽然通过实验验证取得了良好的聚类效果和准确性，但需人工输入相关参数，若参数选取不当则会造成错误的聚类结果。

为了解决现有的障碍空间聚类算法大多都需要人工输入相关参数的问题，本文先引入Voronoi 图来计算反向近邻数，进而确定聚类中心来进行初始聚类，并针对初始聚类结果不精确的问题提出内边界点、外边界点、拓展点、剔除点等概念来提高聚类准确性，理论研究和实验表明本文算法具有较高的准确性。

1 基本定义与说明

（可见点与不可见点）令二维平面上存在的两点、与障碍物集合的交点个数为，若≤1，则称、是相互可见的，、互为可见点；若≥2，则称、互相不可见。

（障碍空间距离）在障碍空间中，如果对象和之间没有障碍，即两个对象互为可视，则障碍空间中两个对象之间的距离为欧氏距离，记为(,)。如果对象和之间存在障碍，则两个对象之间的距离是绕过障碍的最小距离,记为(,)。

如图3 所示，对象和之间存在障碍物,、、、、分别为障碍物的顶点。则和之间的障碍空间距离是绕过障碍物的最短距离：

图3 障碍空间距离Fig.3 Obstacle space distance

(,)=min((,)+(,),(,)+(,)+(,))

（反向第近邻数(x)）对于给定数据集，数据点x作为其他点近邻的次数记为(x)，则(x)称为点x的反向第近邻数。即_(x)={|x∈NN(),∈且≠，符合此条件的数据点的个数为}。

（Voronoi 图）给定一组生成点={,,…,x}∈R，其中2 ＜＜∞，且当≠时，x≠x，其中,∈{1,2,…,}。由x所决定的区域称为Voronoi单元VX，Voronoi 图构成为()={(),(),…,(x)}，其中(x)表示的是x所在的Voronoi单元。

（邻接多边形）共享相同边的Voronoi多边形称为邻接多边形，它们的生成点被称为邻接生成点。Voronoi 单元中存在几条边，就会有几个邻接多边形。

根据Voronoi图的结构和定义可以得出两个基本性质。

（任意两个多边形不存在公共区域）Voronoi 图将数据对象集合中的数据按照其最近邻特性将空间进行划分，生成互不重叠的区域。

（临近特性）生成点x与邻接多边形中的邻接生成点距离最近。

（Voronoi 图的级邻接生成点）给定一组生成点={,,…,x}∈R。 x的级邻接生成点定义如下：

（1）一级邻接生成点(x)={x|(x)和(x)有公共边}；

（2）(≥2) 级邻接生成点AG(x)={x|(x) 和(x)有公共边，∈AG(x)}。

（样本点密度）给定数据集，则其样本点密度可以定义为：

其中，NN()为数据点的近邻数据集，(,)为数据点和的障碍空间距离。

（聚类半径）数据集中所有未聚类的数据点与代表点C的障碍距离均值，即为聚类半径，聚类半径表达式为：

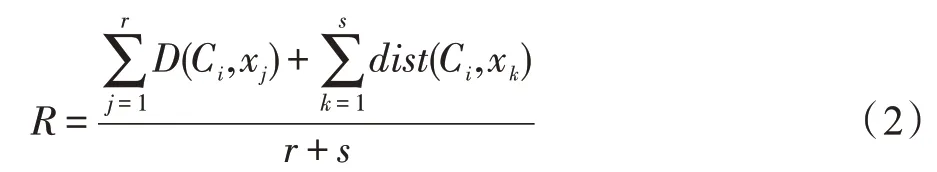
其中，数据集中所有数据点集合为={,,…,x}，为C的可视点集中元素数目，为C的不可视点集中元素数目，+=。

（内边界点、外边界点）初始聚类后，类簇内的点且其所在的多边形的顶点或边与聚类边界有交点，这样的点定义为此类的内边界点。内边界点在聚类圆外的一级邻接生成点定义为此类的外边界点。内边界点作为剔除点的候选集，外边界点作为拓展点的候选集。

（剔除点）计算初始聚类内个点的平均反向近邻数，若内边界点的反向近邻数小于平均反向近邻数，则此内边界点为剔除点。平均反向近邻数计算公式为：

其中，为初始聚类圆中数据点的个数。

（拓展点）在聚类外边界点中找到离内边界点（非剔除点)的距离小于此内边界点在聚类圆内最近的点的距离的点作为拓展点，加入到此聚类中。

如图4 所示，为聚类中心，内边界点集为{,,,,,}，其中假设根据式（2）计算得知又为剔除点。外边界点集为{,,,,,,,,,,}，其中、又为拓展点。

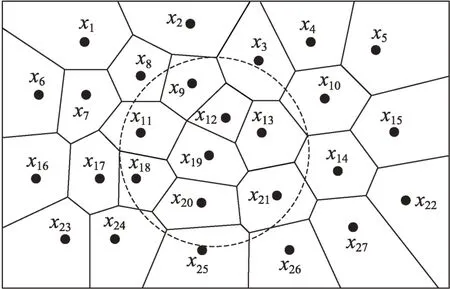
图4 内外边界点、剔除点、拓展点的示例Fig.4 Example of inner and outer boundary points,culling points and extension points

2 基本工作

2.1 聚类中心的选取

初始聚类中心点选取得恰当与否直接影响最终聚类效果的好坏。正确地选取初始聚类中心点会得到较高的聚类准确率，大大缩短算法的时间；相反，中心点选取不当会出现错误的聚类结果，后续对错误的结果进行分析会得出错误的结论。文献[16]提出利用反向近邻数来确定聚类中心，虽然能够恰当地选取聚类中心，但会有较高的时间复杂度或空间复杂度。本文根据Voronoi图的性质对原有算法进行改进，挑选出合适的初始聚类中心，并用这些点进行聚类分析。

由反向近邻数的定义可见，对于一个数据集中的数据点，其_值越大，则说明该点被更多的点包围，直观上它看起来更像数据集的质心。因此，选择从反向近邻数最大的数据点开始构建连通区域。

本节主要利用Voronoi 图来计算反向近邻数，Voronoi 图的邻近特性使得数据点在计算其第近邻时只需计算几个点的障碍距离，而不需要计算出所有点的障碍距离，这大大地减少了计算量，下面给出定理1 用于反向近邻数的计算。

数据点的第+1 近邻一定在的第(1 ≤≤)近邻的邻近单元格内。

当=1 时，的第二近邻点一定在的邻接多边形或者的最近邻的邻接多边形中；当＞1时，假设为的第+1 近邻，且不在的第(≤)近邻的邻接多边形中，则根据Voronoi 图的邻接特性，必有一点使得到的第(≤)近邻的距离小于到的第(≤)近邻的距离。这与题设矛盾，因此假设不成立，从而定理得证。

如图5 所示，假设点、分别为的最近邻和第二近邻，则的第三近邻一定在点、、的邻近多边形中，根据计算得出，点的第三近邻为点。

图5 定理1 的示例Fig.5 Example of theorem 1

使用定理1 可以在已知数据点的第近邻的前提下快速计算出数据点的第+1 近邻，但在障碍空间中，因为障碍物的存在会让两个数据点之间的距离变大，所以在计算距离时需要计算两个数据点之间的障碍空间距离。

如图6 所示，若在点和之间存在障碍物，且(,)大于(,)，则的第三近邻为。

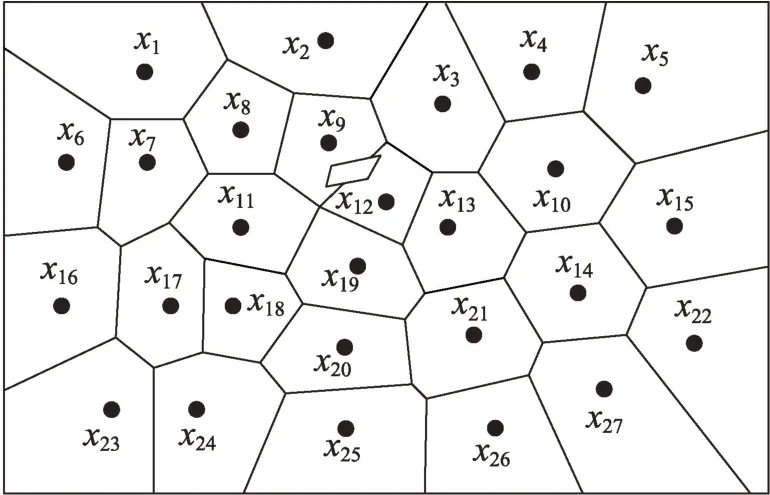
图6 障碍物对计算第k 近邻的影响Fig.6 Influence of obstacles on calculation of k nearest neighbor

根据定理1 提出基于Voronoi 图的反向近邻数的算法V_RkNN，其具体步骤如算法1所示。首先，初始化各个数据点的反向近邻数_(x)=0，从=1开始，根据定理1计算各个数据点的第近邻，若数据点的第近邻为，则_(x)加1。当所有点计算完第近邻后，统计此时没有反向近邻数的点，即_(x)=0 的点的个数，记为() 。如果从-1 近邻到近邻的值不变，则进一步计算每个点的+1近邻，如果值仍不变，则说明此个点相对其他点来说比较分散，且与其他点距离较远，则将_(x)由大到小降序保存在集合中。

V_RkNN 算法

输入：数据集={,,…,x}，障碍物集。

输出：聚类中心候选集合、。

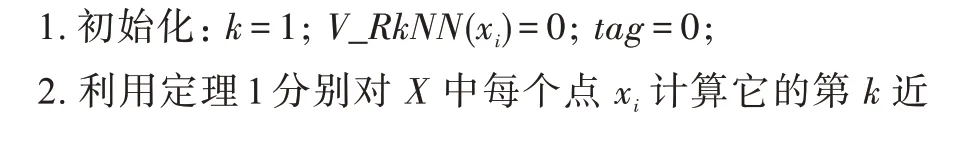
算法时间复杂度和空间复杂度分析：假设数据集中数据点的个数为。步骤2 计算每个数据点的第近邻，其时间复杂度为()，最坏情况下，数据集中每个数据点自成一类，需要计算每个数据点的第近邻，其空间复杂度为()，但是这种情况出现概率较低。一般情况下，其空间复杂度为()，其中≪。步骤6采用快速排序，时间复杂度为(lb)，其空间复杂度为(lb)。综上所述，时间复杂度为(lb)，空间复杂度为()。

2.2 离群点的筛选和剪枝

本节讨论数据集中的离群点处理。离群点是指属性值明显不同于其邻近对象，偏离了大多数数据行为或数据模型的异常数据。离群点的存在使得聚类的质量和效率大大减小，因此在聚类之前去除离群点是非常有必要的一个步骤。下面给出本文离群点的判定定理和判断规则：

_(x)=0 的点一定是离群点。

假设数据点不是离群点，则点必定是某一数据点的第近邻，那么_()必定不为0，这与题设矛盾，因此假设不成立，从而定理得证。

根据样本点密度的定义可知，对于一个数据集中的数据点，其样本点密度越小，则说明该点被更少的点包围，从直观上来看，更可能是离群点。因此从这个角度出发，如果一个数据点的样本点密度低于整个数据集的平均密度，那么它就可能成为离群点。因此本文的离群点还可以从那些处于平均密度以下的数据点中进行筛选和剪枝操作。为了降低算法的计算量，本文利用Voronoi 图进行查找。下面提出规则和定理3 来进行离群点的筛选。

如果一个数据点的一级邻接生成点均为离群点，那么这个数据点是一个离群点。

假设、为两个均低于平均密度的数据点，且数据点的样本点密度大于数据点的样本点密度。如果数据点是离群点，则数据点也一定是离群点。

假设数据点的样本点密度大于数据点的样本点密度，根据样本点密度的定义可知，数据点的样本点密度与其周围的数据点分布有关，如果一个数据点是离群点，那么该数据点则处于一个相对稀疏的区域。由此可知，若数据点是离群点，那么数据点处于稀疏区域，而数据点的样本点密度大于数据点的样本点密度，那么数据点一定处于一个更为稀疏的区域，那么数据点肯定为离群点，从而定理得证。

通过以上论述和分析以及提出的定理和规则，下面给出关于离群点筛选剪枝算法outlierX的主要思想：给定数据集，首先根据算法1对所有_(x)=0的数据点进行剪枝。再计算数据集中的数据点的样本点密度，进而算出平均密度并筛选出所有低于平均密度的数据点，按样本点密度递减顺序进行排序，并存入中。然后，将所有数据点作为生成点，生成Voronoi 图，将集合中的数据点根据样本点密度大小从大到小进行逐个判断是否为离群点，如果数据点是离群点，则从数据集中删除数据点以及中所有位于之后的数据点，并停止判断，离群点筛选剪枝算法过程结束。下面给出具体的离群点筛选剪枝算法outlierX，如算法2所示。

outlierX 算法

输入：数据集={x|=1,2,…,}。

输出：过滤后的数据集′。

算法时间复杂度和空间复杂度分析：假设数据集的大小为，筛选过后的数据集的大小为。算法有三个循环，步骤3～5 的时间复杂度为()，空间复杂度为()。步骤7～11 为第二个循环，遍历了整个数据集，因此时间复杂度为()。第12步使用快速排序的方法对数据集进行降序排序，的大小为，因此时间复杂度为(lb)，空间复杂度为(lb)。第13～18 步为第三个循环，由于遍历的是筛选后的数据集，且遇到数据点是离群点时停止遍历，时间复杂度不大于()。综上所述，该算法的时间复杂度为(lb)，空间复杂度为()。

2.3 广义覆盖圆

在带有障碍物的空间内聚类，由于平面内的距离不能简单地由两点的直线距离来刻画，一般的覆盖圆则失去了效果。本文根据文献[17]，引入广义覆盖圆来解决有障碍物的聚类问题。

在障碍物存在的情况下，定义平面内到聚类中心x的障碍距离等于聚类半径的点的集合叫作x的广义覆盖圆，圆内的所有点即为同属于聚类中心x的类簇的点。

如图7 所示，数据点x为聚类中心，四边形为障碍物，其中|xF|的距离为聚类半径。若不存在障碍物，则初始聚类包含圆中所有点，现存在障碍物，使得数据点集{,,…,}到聚类中心x的距离大于聚类半径，故不在以x为聚类中心、以为聚类半径的初始类簇中。

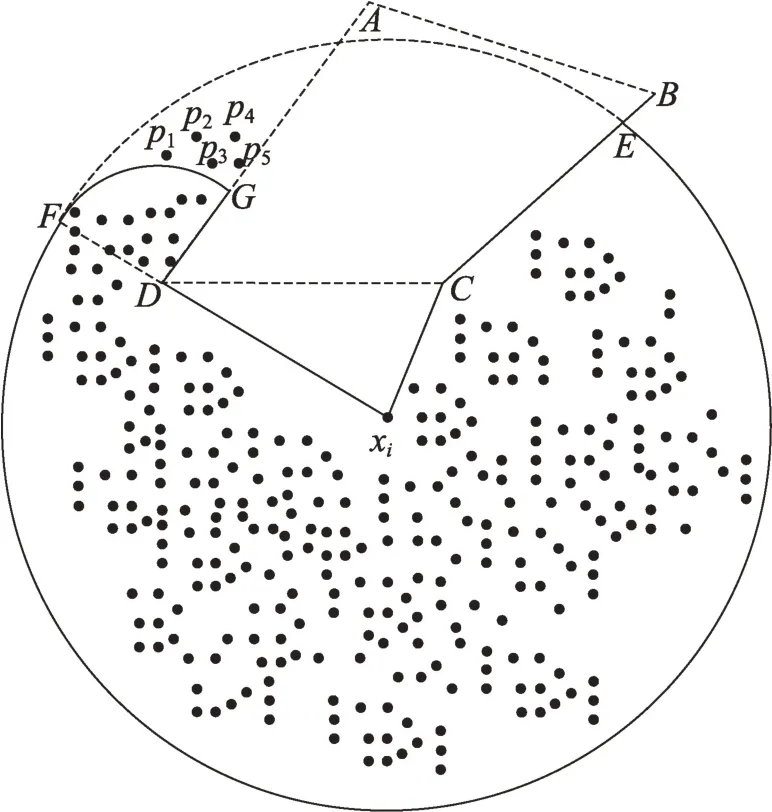
图7 广义覆盖圆的示例Fig.7 Example of generalized covering circle

3 OBRK-means数据聚类算法

基于以上分析和讨论，下面给出障碍空间中的聚类算法（obstacle based on nearest-means，OBRKmeans）的主要思想：首先将数据集中的数据点作为邻接生成点，生成Voronoi 图。根据算法1 得到一个按照反向近邻数由大到小的Hash 表。然后利用算法2 筛选和剪枝离群点，得到新的数据集′。将表中第一个数据点作为聚类中心C，根据式（2）计算聚类半径，若在其中存在障碍物，则形成一个广义覆盖圆进行聚类；反之，则形成一个覆盖圆开始聚类。根据式（3）在聚类内边界找出剔除点并从此类簇中删掉。在覆盖圆内边界点的邻近多边形内找到拓展点加入此聚类中，直到此类聚完。删掉数据集中已聚类的数据点，在剩余点中继续执行以上操作，直至所有点聚类完成。

OBRK-means算法

输入：数据集，障碍集。

输出：障碍空间下的数据聚类结果。

算法时间复杂度和空间复杂度分析：假设数据集的大小为。经过上一章的分析可知第1 步和第2 步的时间复杂度均为(lb)，空间复杂度分别为()和()。步骤3～15 主要是计算聚类半径需要耗费时间，计算聚类半径的时间复杂度为()，并未占用额外的空间。综上所述，总时间复杂度为(lb)，总空间复杂度为()。

4 实验结果与分析

本章主要通过实验对所提出的OBRK-means 算法和文献[12]中提出的DBCCOM 算法进行性能分析与比较。实验硬件环境为8 GB 内存，IntelCorei5处理器，Windows10 操作系统，程序用Java编写。

UCI数据集是公认、公开的机器学习数据集，许多聚类算法都使用其验证聚类算法准确率和有效性。因此本文选择UCI 数据集中的数据作为本文实验的真实数据集，实验所需数据集的详细情况如表1所示。

表1 UCI实验室数据集Table 1 UCI laboratory datasets

实验主要考虑四方面因素：数据基数、障碍物数量、CPU 运行时间、聚类质量。利用以上四方面作为衡量算法的指标。

常用的聚类有效性评测有内部评价法、外部评价法和相关性测试评价。它们能对聚类结果进行评价，得出聚类结果是否最优。实验采用F-measure 熵作为聚类外部评测标准，简写为F 值。用轮廓系数（Silhouette coefficient）作为评价聚类内部有效性的指标，简写为S 值。

分别对各个算法进行100 次独立聚类实验，统计每次实验的结果，然后对每种算法求100 次实验结果的平均值，对比算法的实验结果如表2 如示。

表2 算法评测有效性对比Table 2 Comparison of effectiveness of algorithms

结果显示，对于以上4 组数据集，OBRK-means算法的F-measure 指标平均值和S 指标平均值均高于DBCCOM 算法的评测指标。通过实验可看出，OBRK-means算法表现出更好的聚类效果。

接下来从样本数目和障碍物对聚类结果的准确率和CPU 响应时间的影响进行分析。具体情况为：对于聚类算法的准确率来说，无论是增加样本数目还是障碍物的数目，OBRK-means 算法的性能更优。OBRK-means 算法和DBCCOM 算法的CPU 响应时间均随着样本数目和障碍物数量的增加而增加，但本文提出的OBRK-means算法因使用Voronoi图进行距离度量更高效，其时间复杂度为(lb)，而DBCCOM的时间复杂度为()，因而相比之下本文算法的CPU 响应时间更少。

由图8 到图11 的折线趋势图可知，与聚类算法DBCCOM 相比，本文提出的OBRK-means 算法在处理障碍空间中的数据集时所得聚类结果的准确率和精度更高，这说明使用OBRK-means 算法聚类出的数据，类内紧密度更高，类间相似度更小。因此本文提出的OBRK-means 算法在处理障碍空间中的数据时，所得聚类结果更好。

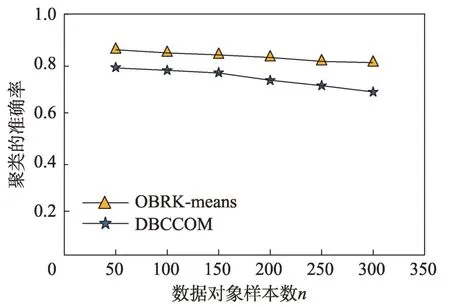
图8 样本数目对准确率的影响Fig.8 Effect of sample size on accuracy

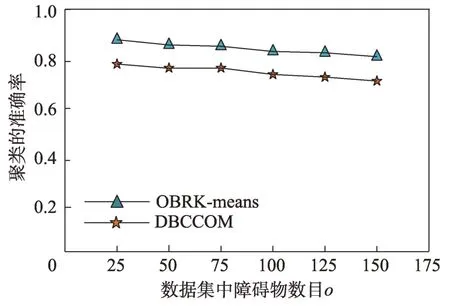
图9 障碍物数目对准确率的影响Fig.9 Effect of obstacles on accuracy

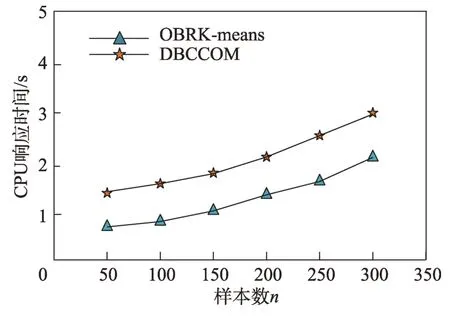
图10 样本数目对CPU 响应时间的影响Fig.10 Effect of sample size on CPU response time

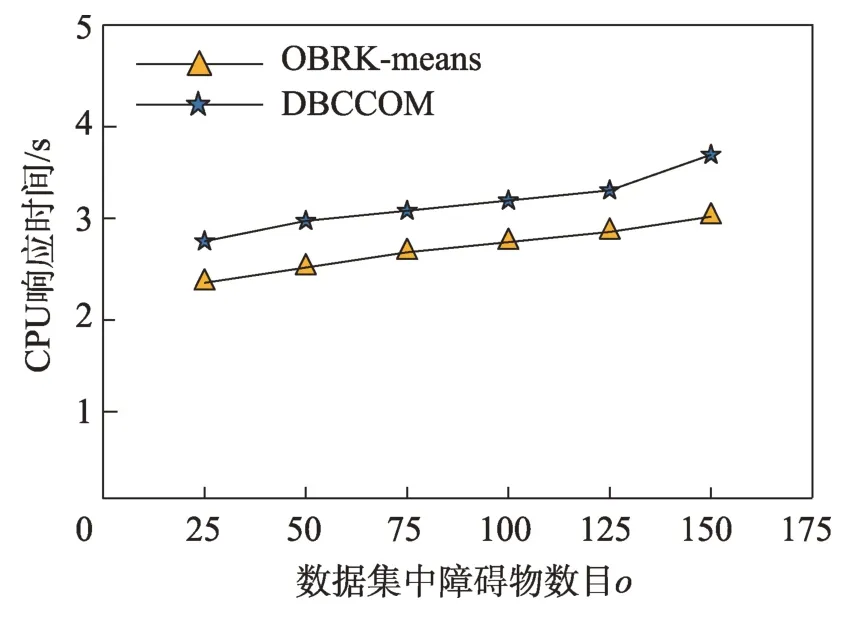
图11 障碍物数目对CPU 响应时间的影响Fig.11 Effect of the number of obstacles on CPU response time

5 结束语

障碍空间的聚类算法在现实生活中有着非常广泛的应用，本文提出的OBRK-means 算法首先引入Voronoi 图计算反向近邻数来确定聚类中心，再利用Voronoi 图和样本点密度进行离群点的筛选，最后针对初始聚类结果不精确的问题提出内边界点、外边界点、拓展点、剔除点等概念来提高聚类准确性，达到了理想的聚类效果。

障碍空间中的聚类算法有着广泛的实际应用，接下来，将对不同障碍物情况下的聚类问题进行研究，并对移动对象在障碍物约束下的聚类问题进行研究，使聚类结果更能反映真实地理情况，更有实用价值。