基于数字液压动力管理系统的混合执行器控制研究

姜海莲

(吉林铁道职业技术学院铁路机车学院，吉林吉林 132000)

0 前言

变速液压驱动器广泛应用于飞机，现在也开始应用于数控机床、折弯机、机器人等固定设备。有较多的油路形式可供变速液压驱动器选择，但这些油路显示出电输入功率和机械输出功率之间的一对一关系，即液压系统用作电输入和机械输出之间的传递系统。因此，必须根据执行器的峰值功率确定电机的尺寸。通常平均功率要小得多，这就意味着电机和电力电子元件尺寸过大，价格昂贵。因此，开发新型混合执行器，建立新型混合执行器数学模型，研究新型混合执行器控制具有重要意义。

文献[2-3]利用电机和气缸的优点，设计了气-电混合执行器，介绍了其原理及结构，建立气-电混合执行器数学模型，在MATLAB软件以及实验平台上验证了该气-电混合执行器的可行性。文献[4-5]提出了一种液-电混合直线驱动系统，建立了系统简化模型，通过扩张状态观测器估计系统的干扰力，同时用滑模算法精确控制直线执行器位置，最后通过仿真和实验证明该液-电混合直线驱动系统的合理性。文献[6-7]设计了直驱式电液执行机构，介绍了其工作原理，建立了直驱式电液执行机构的数学模型，引进花授粉算法整定PID参数，最后通过仿真验证该直驱式电液执行机构的有效性。以上研究中系统设备需要根据执行机构的局部峰值功率进行选型，从而增加了系统成本，造成资源的浪费。对此，本文作者提出一种基于数字液压动力管理系统的混合执行器。构建新型混合执行器简化液压回路图，建立数字液压动力管理系统、液压回路以及变速电动伺服电机动力学模型；采用基于模型的控制器，利用成本函数实现最优控制。在MATLAB软件中对基于数字液压动力管理系统的混合执行器进行仿真验证，与传统阀控执行器的仿真结果进行对比，为混合执行器控制研究提供参考。

1 混合执行器数学建模

图1所示为基于六活塞数字液压动力管理系统的混合执行器的简化液压回路。变速电动伺服电机作为原动机。单杆液压缸的A腔由数字液压动力管理系统的出口A控制，A线中使用小型阻尼蓄能器平滑活塞运动。数字液压动力管理系统的出口HP连接到较大的蓄能器和液压缸的B腔 。LP蓄能器为储罐。

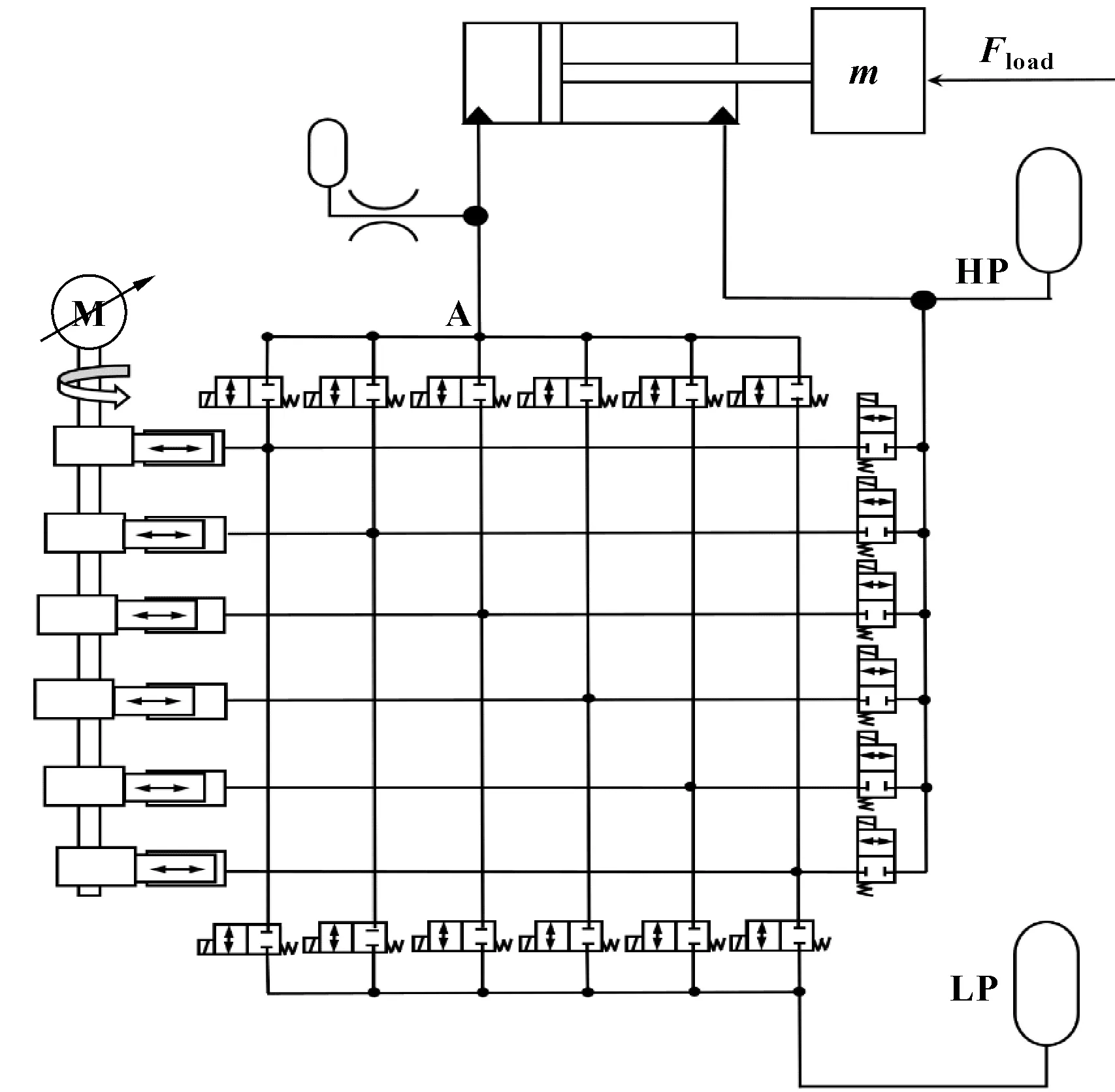
图1 数字液压动力管理系统的混合执行器简化回路

1.1 数字液压动力管理系统数学模型

假设：(1)泵活塞为正弦运动曲线；(2)泵送活塞为6个；(3)使用平方根模型对通过控制阀的流量进行建模。数字液压动力管理系统和电机的扭矩平衡方程为

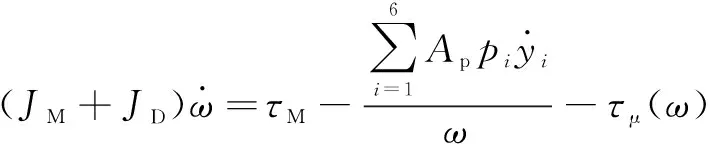
(1)

忽略压力对摩擦的影响，得到的扭矩损失模型为

()=sgn()+

(2)

其中：为库仑转矩；为黏滞摩擦系数。在后续控制器设计时需要在控制器中估算由控制阀中的流量损失引起的扭矩，该扭矩为

(3)

其中：为泵送活塞的冲程；为控制阀的流量系数；为数字液压动力管理系统的摩擦因数。

1.2 液压回路数学模型

假设液压缸的活塞等效面积比为2∶1，同时模型中管道和油缸室为具有恒定体积模量的集总体积。通过使用绝热模型和湍流端口将蓄能器建模为理想模型。活塞的力平衡方程为

(4)

其中：为负载的质量；为活塞位置；为液压缸A室中的压力；为无杆腔活塞面积；为数字液压动力管理系统出口HP处的压力；为有杆腔活塞面积；为摩擦力；为负载。

执行器的摩擦力使用动态摩擦模型：

(5)

其中：为油缸密封件的挠度；为密封件的刚度；为静摩擦力；为库仑摩擦力；为确定最小摩擦的速度；为密封件的阻尼系数；为黏滞摩擦系数。

1.3 变速电动伺服电机数学模型

电动伺服电机是在磁场定向控制模式下运行的永磁同步电动机。假设：(1)电磁力为正弦波；(2)使用表面安装的永磁体，电感和等于常数；(3)不考虑电量饱和；(4)转速目标值的最大比率受限。

文中模型建立在转子的直轴和正交轴(d-q)上。通过以下微分方程求解电流：

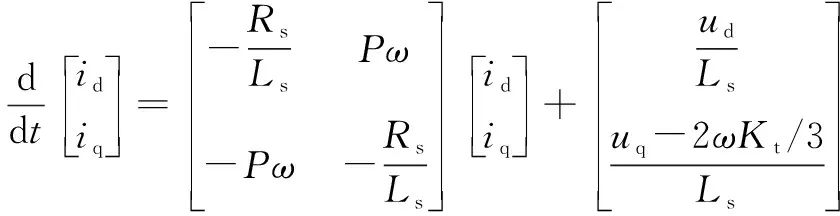
(6)

其中：和为d-q系统中的电流；和为d-q系统中的电压；为定子电阻；为d-q轴上的电感(==)；为极对数;是电动机的转矩常数。

转矩由控制，并且控制器试图将保持为零。假定电流和转速由PI控制器控制,电机产生的电磁转矩为

=-

(7)

其中：为黏滞摩擦系数。

2 控制系统

混合执行器控制的最终目的是尽可能使活塞的位置以及速度与期望值和保持一致。由于混合执行器精确模型的建立比较困难，传统PID控制器参数集在运行过程中固定不变，对于处理这种复杂的控制问题存在局限性。因此，开发基于模型的系统控制器。

2.1 活塞控制

数字液压动力管理系统的出口A用于控制活塞速度。稳态活塞速度为

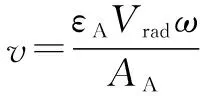
(8)

其中：为数字液压动力管理系统的角位移；出口A的虚拟排量定义使用哪个主要流量(-1，-0.5，0，0.5，1)。

控制运动方向的一种方法是对使用正值，并在两个方向上旋转电动伺服电机。但是，数字液压动力管理系统输出流的延迟与转速成反比，低速时会形成阻碍。另一种是使用正并更改的符号。文中使用第二种方法。为避免较长的系统延迟，假定电动伺服电机的转速高于。这样，当=0.5时，活塞的最小正速度为

(9)

=1时活塞的最小速度为

(10)

全排量时的最大速度为

(11)

最大和最小速度之比为

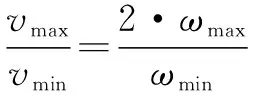
(12)

给定参考速度和虚拟排量的转速目标值计算公式如下：

(13)

正向速度的控制原理：

(1)当速度参考值低于/2时，转速设置为并且设置为0;

(2)当速度参考值在/2和之间时，转速设置为并且设置为0.5;

(3)当速度参考值在和之间时，通过方程(13)计算转速，并将设置为0.5;

(4)当速度参考值大于时，通过方程(13)计算转速，并将设置为1。

负向速度的逻辑原理类似。通过以上控制逻辑可将转速降至最低，以减少摩擦和流量损失。

通过将速度前馈与P位置控制器相结合来实现闭环控制：

=+(-)

(14)

其中：为前馈路径的增益；为P控制器的增益。

2.2 数字液压动力管理系统控制

HP出口压力用于在负向运动上产生力，因此具有取决于系统负载曲线的最小值，但是它不能超过系统最大压力。将目标压力设置为最大和最小压力的平均值：

(15)

HP压力导数的计算公式为

(16)

其中：为HP管路、B腔和HP蓄能器的组合液压容量；为出口HP的虚拟排量。蓄能器控制电容约为

(17)

其中：为蓄能器体积；为预加油压力。电容大意味着HP压力在一个采样周期内不会显著变化。出口HP的相对排量应使得HP压力与参考值相差不大，并且数字液压动力管理系统的扭矩足够小。因此，数字液压动力管理系统旋转所需的扭矩为

=(-)+()+()+

(-)

(18)

的限制条件为

(19)

其中：为电动伺服电机的最大转矩。这些限制条件不考虑由加速或减速引起的转矩。其他限制条件来自数字液压动力管理系统的几何约束，用式(20)表示：

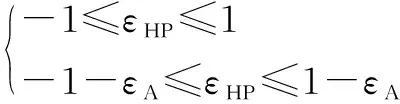
(20)

使用以下成本函数得到最佳控制

=()+|Δ|+[()-

(21)

其中：第一项将扭矩保持在零附近；第二项惩罚的变化；第三项将HP压力推向目标值。针对变化的值，对满足方程式(19)和(20)的成本函数进行评估，并选择使成本函数最小的值。通过主流量控制器将和值转换为相应的阀控制序列。因此，通过基于模型的控制器可以对参数时变且高度非线性的混合执行器进行有效控制。

3 仿真模拟

为对比基于数字液压动力管理系统的混合执行器与传统阀控执行器的轨迹跟踪效果，在MATLAB/Simulink环境下，对混合执行器进行仿真。混合执行器仿真模型如图2所示。仿真参数如下：=0.04 kg·m；=0.02 kg·m；=0.8×10m；=2.3 N·m；=0.064 N·m·s/rad；=0.01 m；=2.1×10m/(s·Pa)；=5.2×10N·m·s/rad；=6 000 kg；=0.4×10m；=0.2×10m；=3×10N/m；=3.5×10N·s/m；=470 N·s/m；=460 N；=600 N；=0.004 m/s；=5.12 mΩ；=0.05 mH；=6；单位电流下的输出转矩=0.1 N·m；=0.003 N·m·s/rad；=2 L；=12 MPa；=0.8；=5；=40 N·m；=1 000 r/min；=3 000 r/min；=5 MPa；=25 MPa。传统阀控执行器采用PID控制器，参数为=5、=0.5、=0.01。

图2 混合执行器的Simulink仿真模型

基于数字液压动力管理系统的新型混合执行器与传统阀控执行器的活塞位置和速度响应分别如图3和图4所示。可知:基于数字液压动力管理系统的混合执行器活塞位置和速度曲线与期望曲线最接近，跟踪误差最大分别为1.2 mm和2.3 mm/s；而传统阀控执行器位置和速度跟踪误差较大，分别为3.1 mm和4.3 mm/s。

图3 新型混合执行器和传统阀控执行器的位置响应

图4 新型混合执行器和传统阀控执行器的速度响应

进一步测试系统的输入功率变化，结果如图5所示。可以看出：传统阀控执行器输入的平均功率较高，同时具有较大的峰值；基于数字液压动力管理系统的混合执行器使用液压蓄能器处理功率峰值，电动伺服电机仅向系统提供较低的平均功率。

图5 新型混合执行器和传统阀控执行器的输入功率 图6 新型混合执行器和传统阀控执行器的系统能耗

传统阀控执行器和基于数字液压动力管理系统的混合执行器能耗曲线如图6所示。可知：传统阀控执行器的能耗高达12.3 kJ，基于数字液压动力管理系统的混合执行器多余的能量存储在蓄能器中，因此能耗减少约41%。

因此，采用基于数字液压动力管理系统的混合执行器的活塞位置和速度跟踪性能好，输入功率无较大波动，同时具有较高的能源效率。

4 结论

本文作者提出了一种基于数字液压动力管理系统的新型混合执行器，构造了新型混合执行器简化示意图，建立了新型混合执行器系统动力学模型。开发了不依赖精确系统动力学模型的控制器——基于模型控制器。在MATLAB中对基于数字液压动力管理系统的新型混合执行器控制响应、输入功率以及能耗进行仿真验证。同时，与传统阀控执行器仿真结果进行对比和分析。结果表明:采用基于数字液压动力管理系统的新型混合执行器，系统不仅可控性强，需要的输入功率和能耗也大大减少。研究结果为混合执行器控制的研究提供参考。