追问“解决问题的策略”教学的有效策略

◇沈 琦（江苏：苏州市吴江区思贤实验小学）

“解决问题的策略”是苏教版教材编写的一个系列内容，从三年级开始，每个学期学习一种解决问题的策略。在教学中，教师常常使用这样的教学模式：呈现问题—激发策略需要—感悟策略—归纳策略—形成策略。学生在经历了这一系列活动后，最后能灵活使用各种策略解决问题。这是理想的教学模式，但是在现实教学中，“解决问题的策略”的教学现状堪忧。

一、“解决问题的策略”的教学现状

笔者对本校64 位数学教师关于“解决问题的策略”教学进行问卷调查，从问卷调查中发现，70.31%的教师将“解决问题的策略”等同于过去的应用题，这是一种与课程标准不相符合的教学观念。在教学中，76.56%的教师采用讲授法，使学生学会课标要求的相关数学题目。这样的教学观念导致42.19%的教师在教学时认为，解决问题的关键是发现问题，明确数量关系；46.88%的教师认为，关键是能正确列式并解答。这样的教学是达不到《义务教育数学课程标准》的目标的，即“使学生初步学会从数学的角度提出问题、理解问题，并能综合运用所学知识和技能解决问题，发展应用意识；形成解决问题的一些基本策略，体验解决问题策略的多样化”。从上述的调查数据中可以发现，按照目前教师的这种教学态度，学生在“解决问题的策略”这类课中，获得的只是一种正确解题的能力，并非能在数学上有所发展，也根本不能形成数学素养。

二、“解决问题的策略”的教学价值

（一）有助于提供解决问题的经验

教材中“解决问题的策略”一般都是创设一个与学生生活相关的情境，让学生在情境中解决问题。从三年级第一次接触“解决问题的策略”开始，都是让学生在生活经验与解决问题的经验共存的基础上，螺旋提升难度，让学生提出问题，进行思考、分析，在尝试解决问题的过程中，进一步积累经验，丰富经验，感受策略的应用价值。为日后学生解决现实生活中的数学问题提供方法与经验，真正体现数学与生活的联系。

（二）有助于促进数学思维的发展

学生解决问题的过程其本质是一个严密、连贯的思维活动的过程。学生在策略形成、体验、内化、应用的过程中，感受到思维层层深入，感受到思维的变化，从而产生因思维变化而带来的学习成就感。例如，苏教版三年级上册《解决问题的策略——从条件出发》一课，学生学习后会提出这样的问题：既然解决问题的策略可以从条件出发，那在一些其他解决问题中是否能从问题出发呢？这样的提问是学生思维的变化，学生已经能从所学策略中衍生出新的策略，并且会主动思考：什么样的问题要用从条件出发的策略？什么样的问题要用从问题出发的策略？这是一种思维的发展与提升。

三、追问——“解决问题的策略”教学的有效策略

“解决问题的策略”教学价值深远，问卷调查显示，教师在此类教学中存在一定的问题。那么如何改变教师在这类教学中的教学方式，让“解决问题的策略”这类教学更加有效呢？

教育研究表明：学生学习的过程其实是一个认知由平衡到不平衡再到平衡的过程。而课堂追问能打破这个平衡，激发学生学习的需要，促进他们进行深度学习，从而实现数学思维的发展与延伸。所以在“解决问题的策略”教学中，教师可以采用追问策略，让学生的学习从知识性走向思维性，使教学更加有效，使学生的数学思维在课堂中得以发展。

（一）在策略孕伏阶段追问，激发策略需要

教育家苏霍姆林斯基认为：“教学和认识周围世界的过程充满情感，这种情感是发展儿童智力和创造力的极其重要的土壤。如果教师不想办法使学生产生情绪高昂和智力振奋的内心状态，就急于传授知识，不懂情感的脑力劳动就会带来疲倦。”可见，情境是学生学习的重要土壤，创设情境是非常重要的教学方法。

如，在教学《解决问题的策略——列举》一课时，教师创设了这样的问题情境：国庆假期里，我来到了一个农庄玩，你也想去看看吗？农庄里的王大叔想用22 根1 米长的木条围一个长方形花圃，怎样围面积最大呢？王大叔想了很久还是没有想到好的解决办法，大家愿意来帮助王大叔解决这个问题吗？于是，学生在帮助王大叔解决“如何围面积最大”的问题情境中展开思考。学生从学习经验中知道这个问题需要寻找新的办法解决，也就是有了新策略的萌芽。但是新策略到底是什么，还需要在教师的追问下才能萌发。但若光有情境，没有教师的追问，学生也无法在情境中形成思考。教师要不断地追问：从这些文字中你读到了什么？也就是让学生理解题意。学生发现：围成的长方形的周长是22 米，围成的长方形的长和宽必须都是整米数，可以围成不同的长方形。教师继续追问：“用什么方法可以找到面积最大的长方形？”在教师的追问中，学生激发了寻找新策略的需求。学生发现：由于可以围成的长方形有多种，必须进行列举，才能找到面积最大的长方形。学生在这样的问题情境中，在教师的追问下思考需要什么新的策略解决问题。

（二）在策略形成阶段追问，形成策略意识

在学生产生了学习新策略的内需后，教师将引导学生自主探索策略，形成新的策略。策略的形成需要学生自主去探索、去发现。如，在教学《解决问题的策略——假设》一课时，教师出示例题：小明把720 毫升果汁倒入6 个小杯和1 个大杯，正好倒满，问一个大杯、一个小杯的容量各是多少？

学生通过独立思考，发现以过去的学习经验根本解决不了这个问题，于是有学生提出了这样解决的方式：设小杯的容量为X 毫升，大杯为4x，4X+6X=720。

教师追问：这个4X 是什么意思？你如何获得的？

学生：4X是我看图估计出的大杯的大小。

教师继续追问：为什么要估计出大杯的大小？

学生：都要变成一样的，也就是要知道一个大杯是几个小杯的容量。

在教师的追问下，学生用模糊的数学语言表达“都要变成一样的”，这是“假设策略”的原生态样子。教师的追问引发学生深入思考，学生发现：原来杯子数量是不同量，要假设成相同量才能解决问题。

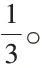
一般这个时候很多教师就满足了，认为已经达到了解决问题的目的，学生也会用假设的策略解决这个问题，于是就会“很顺利”地进入下一个环节。其实，这个时候学生最多是对这个题型有了了解，但并未真正建立数学模型。数学思维也并未有太多的变化。聪明的学生都知道这节课就是学习这种类型的题型，所以这节课的所有题目都可以照搬“假设策略”的套路。但是，为什么是用假设策略，可能更多的学生没有明白，学生的策略意识并未真正建立。所以一旦题目不按常规套路出现，学生就不会解决。如果在此环节教师不继续追问，那么学生在课堂上仅仅是解决了问题，并未形成策略意识。所以在此环节教师必须继续追问：为什么要把不同量假设成相同量呢？引发学生继续深入思考：如果不把不同量假设成相同量，那么，问题无法解决。这样的追问让学生从正向思维与逆向思维两个角度对此类问题有了更深入的理解，深化了策略意识，而不是仅仅局限于这道题目。

策略是对方法的本质认识，解决问题的方法可以通过做题传授，但是策略意识的形成并不能只靠一道例题，更需要学生在策略形成的过程中不断追问。教师追问问题的本质才能使学生真正形成策略意识。当学生形成策略意识后，数学思维也在这个过程中发生了质的变化，学生的数学思维已经从简单模仿进阶到主动建构。

（三）在策略应用阶段追问，深化策略价值

策略形成后，策略的价值只有在应用中才能凸显，也只有在应用中才能深化策略价值。策略的应用阶段是进一步熟练应用策略进行变式练习。这些变式练习中的追问使得学生能主动思考，灵活运用策略，深化策略价值。如，在《解决问题的策略——列举》一课中，教师设计了这样的练习活动：王大叔工作的农场附近有公交车，王大叔每天都是坐公交车回家，公交车的上午发车时间首班6:00，末班11:00，下午发车时间首班13:00，末班19:00，每隔40 分钟发一班车。王大叔16:00 下班，应该选择几点发的车合适？教师在抛出这样一个问题后，学生应用策略解决问题。如果教师直接让学生解决这个问题，那么学生肯定会遇到很多困难。如何帮助学生获取有效信息呢？教师首先追问：解决这个问题的有效信息是什么？学生发现“公交车的上午发车时间首班6:00，末班11:00”这个信息对解决这个问题没有作用。于是学生利用“下午发车时间首班13:00，末班19:00，每隔40分钟发一班车”这个信息进行一一列举。学生的列举会出现两种情况，一种是列举到16:20 结束，另一种是列举到17:40 结束。面对两种不同的结果，教师继续追问：为什么到16:20 就结束列举？学生经过思考发现，原因是王大叔16:00 下班，16:20 乘车回家是最合适的。这样的追问，能使学生根据具体的情境，灵活应用策略，深化策略价值。

“问题是数学的心脏”，学习数学离不开解决问题，但解决问题不是目的，它是为了让学生加深对知识的理解，强化技能训练，提高问题解决的策略意识，提高思维能力、解决问题的能力，培养创新精神和实践能力。这样，学生在解决问题的过程中学会正确的思维方法和解题策略就显得尤为重要。而教师在策略运用阶段的追问就能让学生真正灵活运用策略，将策略真正落到实处。

在“解决问题的策略”教学中，如果不提策略，学生也会在理解题意的基础上正确解答，就像在对教师的问卷调查中，很多教师把“解决问题的策略”等同于“应用题”。但是学会方法并不是教材设计的初衷，“形成解决问题的一些基本策略，体验解决问题策略的多样性，发展实践能力和创新精神”才是《义务教育数学课程标准》的要求，也是教学的归属。有效“追问”是激活学生思维、促进学生构建知识，进而优化课堂教学的重要教学策略。作为课堂教学中的一种策略，使得“解决问题的策略”课堂教学更加深入，更加有效，让策略真正根植于学生心中。