城市轨道交通列车节能运行研究

文/段玉琼

列车运行能耗受线路条件、编组方案以及操纵策略影响较大。为了更准确地研究列车节能运行问题，研究列车在运行过程，分析线路条件、编组方案及操作策略对列车运行能耗的影响，提出基于操纵序列的节能优化方法，采用人工蜂群算法进行节能优化，并通过Matlab进行仿真验证。研究发现，本文所采取的方法能达到降低列车节能运行的目的，对其他交通工具的节能运行具有较好的参考意义和价值。

引言

随着城市轨道交通建设和运营规模不断扩大的同时，总体能耗呈逐年增长趋势。截至2020年，城市轨道交通运营里程已达7969.7公里，所用的总电能耗达到172.4亿千瓦时，相比2019年增长了12.9%，其中用于列车牵引的能耗高达84亿千瓦时，同比增长了6.3%[1]。因此，有必要研究列车节能运行问题。根据统计数据可知，在列车能耗系统中牵引净能耗所占比例高达60%，因此，本文研究城市轨道交通列车节能运行问题的出发点是如何降低牵引净能耗。

1.城市轨道交通列车运行过程分析

为了真实模拟列车运行过程，须准确描述列车受力情况，建立准确的列车牵引计算模型、运动学模型和运行过程模型，推导出列车单位合力、加速度、速度、距离与运行工况之间的关系，为研究列车节能运行提供必要的基础理论。

1.1 列车牵引计算模型

本文采用单质点模型，对列车受力分析可得其所受到的单位合力如式1所示。

其中，f为单位牵引力；w0为单位阻力；wj为附加阻力；b为单位制动力。

1.2 列车运动学模型

根据牛顿第二定律和运动学公式可得，列车运行过程中单位合力、加速度、速度、时间和距离之间的关系如式2所示。

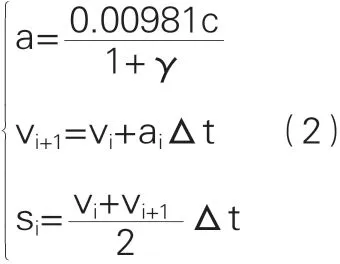
其中，γ为回转质量系数；vi、vi+1分别为第i、i+1步的列车速度；ai为列车运行加速度；Δt为时间步长，s；si，si+1为第和步列车运行距离。

1.3 列车运行过程计算及工况转换

列车运行过程实际上就是牵引、惰行和制动工况之间的相互转换，且三者工况间的迭代公式相同，如式3所示。

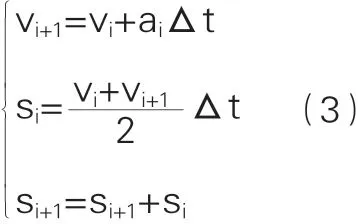
其中，vi，vi+1为第i、i+1步的列车速度；ai为运行加速度；Δt为时间步长；si，si+1为第和步运行距离。

1.4 列车运行能耗计算

为有效降低列车牵引净能耗，本文通过优化列车司机在区间运行时所采取的操纵序列，从而达到列车节能运行的目的。列车运行能耗E的计算模型如式4所示。

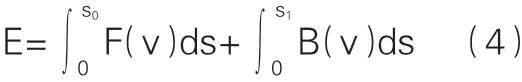
其中，F（v）为牵引力；s0为牵引运行距离；（v）为制动力；s1为制动运行距离。

2.线路条件、编组方案及操纵策略对列车运行能耗分析

影响其运行能耗的因素有很多，其中主要影响因素有线路条件、列车编组方案、司机操纵策略及操作方式等。线路的坡道及曲线半径的大小等会对列车运行能耗产生影响，尤其是坡道数据，随着坡度的加大，列车运行能耗呈线性上升。不同的列车编组方案会产生不同的能源损耗，根据相关统计数据，运量相同的情况下，三节编组的能耗相对于四节和六节编组分别增加20.9%和69.8%[2]。在调速过程中，司机根据列车的运行状态、自身特征所采取的不同操纵策略会影响到列车能耗，不同操纵策略产生的列车能耗差异可高达30%[3]。因此，在列车节能运行优化研究中，应充分利用线路情况，选择合理的编组方案和操纵策略，优化列车运行过程中的操纵序列进而使得列车以最节能的方式运行。

3.基于操纵序列的节能优化

对于列车运行节能的优化，其实质是寻找满足运行时间、距离和速度等约束条件的列车运行能耗最小的工况转换点位置，即为一个多维约束问题的优化。本文采用智能算法解决列车节能运行优化这一多维约束问题，优化列车运行过程中的工况转换点位置，即列车的操纵序列，从而得到列车运行能耗最小的工况转换点位置。

4.列车节能运行优化研究

通过对比群智能优化算法可知，人工蜂群算法(ABC)与PSO算法和DE算法相比较，具有优良的性能[4]。因此本文采用人工蜂群算法进行列车节能运行优化问题的计算。为有效验证ABC算法的优越性及可行性，分别采用ABC算法、PSO算法和DE算法对基准测试函数式5进行优化测试，得到函数的三维图形及优化收敛曲线如图1、2所示。

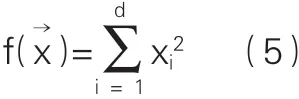
图1 基准测试函数三维图形

由图2可知，ABC算法相比较PSO算法和DE算法，其收敛速度较快、最优解精度较高，且不易陷入早熟。由此可知，在函数极值寻优计算中，ABC算法优于PSO算法和DE算法。本文的思路是让列车按照运行计划，在满足安全运行、正点停车、精准停车的前提下，以最节能的操纵序列在区间安全运行。由此，可建立如式6所示的列车节能操纵优化模型。在模型求解过程在，将整个运行过程划分为n个时间步长，每个时间步长的能耗累加得到整个列车运行过程的总能耗。

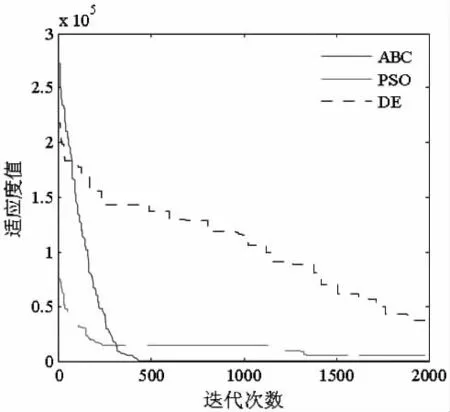
图2 基准测试函数收敛曲线

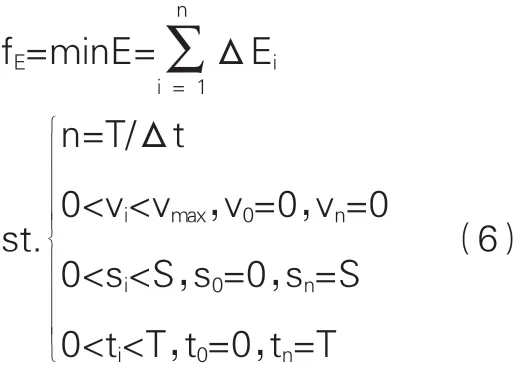
其中，Ei为第i个时间步长的能耗；Vmax为列车运行最大速度；S为列车运行距离；T为列车运行时间。

根据上述列车节能优化模型中的速度、时间及距离约束构造惩罚函数，具体惩罚函数叙述如式7所示。

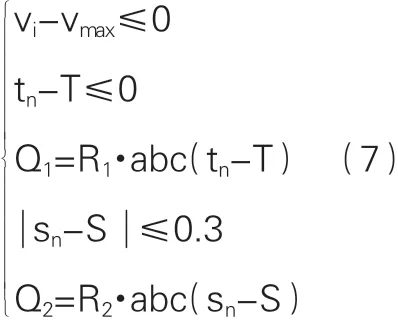
其中，vi为实时列车运行速度；vmax为线路限速；tn为列车实际运行时间；T为列车运行图定时间；Q1为时间惩罚函数；R1为时间约束惩罚因子（R1=106）；sn为列车实际运行距离；S为列车运行图定距离；Q2为距离惩罚函数；R2为距离约束惩罚因子（R2=106）。

根据人工蜂群算法的原理，结合列车节能运行优化问题，得到基于人工蜂群算法的列车节能优化流程，如图3所示。

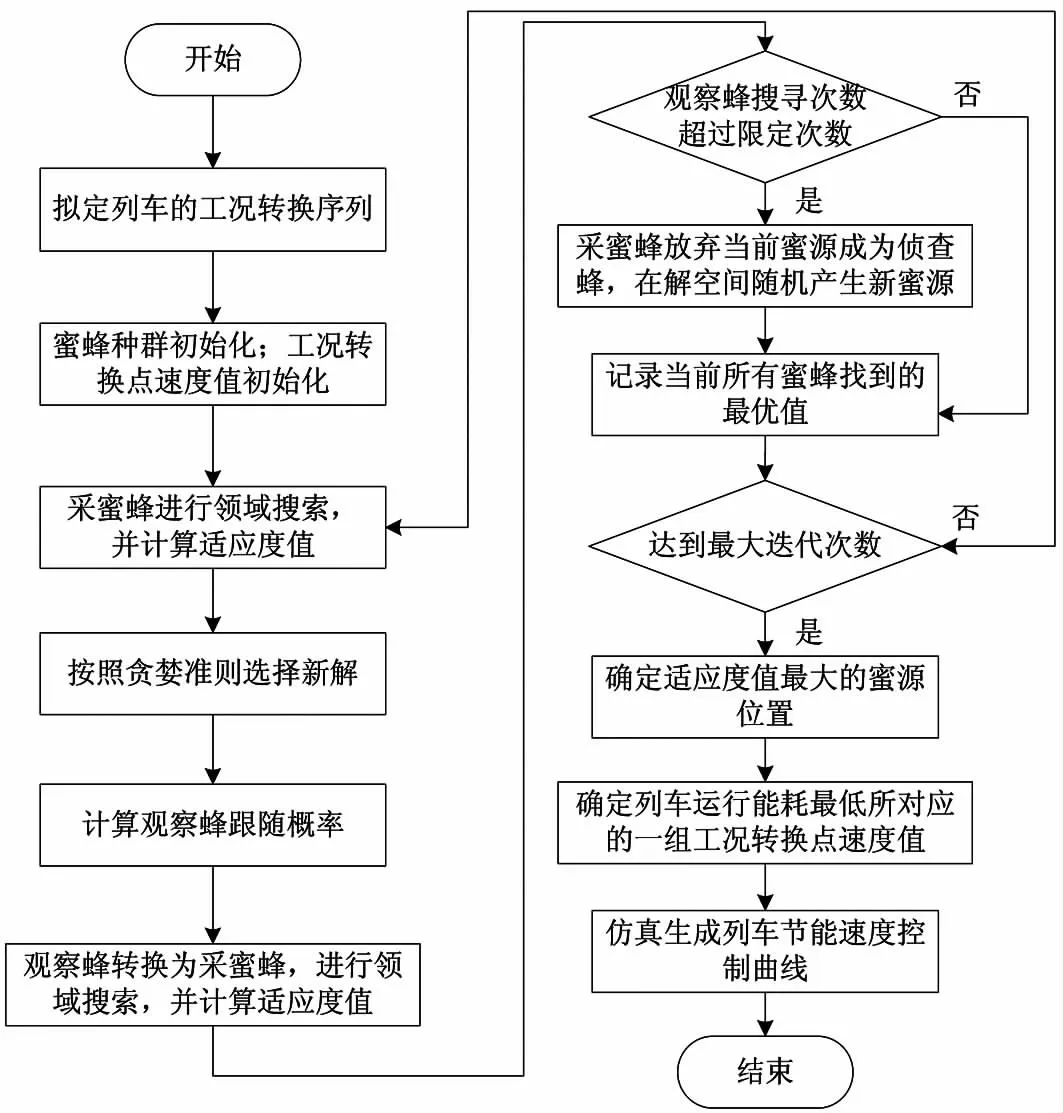
图3 基于人工蜂群算法的列车节能优化

利用图3中优化流程来确定适应度值最小时所对应的蜜源位置，即列车运行能耗最小时所对应的工况转换点位置，得到优化后的列车运行速度曲线。

5.仿真结果与分析

本文以实际列车运行数据为根据，利用人工蜂群算法优化列车运行曲线，通过比较优化后的仿真结果，进而验证本文所提方法的有效性。以北京地铁亦庄线为例，线路纵断面图如图4所示，次渠南-经海路站间距离为2091m，运行总时长为140s，站间牵引能耗为7.25×107J，列车为B型车辆，列车参数如表1所示。

图4 线路纵断面图

表1 仿真列车主要特性参数

根据线路特征，制定“牵引、惰行、牵引、惰行、制动”操纵序列，采用人工蜂群算法进行仿求解，得到优化后的列车运行速度曲线、运行工况转换如图5、6所示，性能指标如表2所示。

表2 性能指标与分析

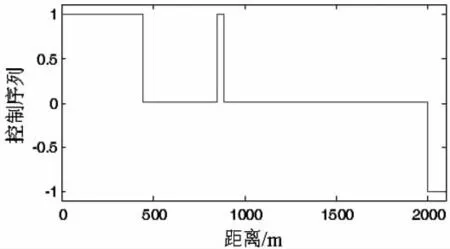
图6 优化后的列车运行工况序列图

由仿真结果可知，列车按照优化后的运行速度曲线运行时，在满足安全运行、正点停车（停车误差0.26s）、精准停车（停车误差0.28m）的要求下，其运行能耗为6.56×107J，相比较实际线路列车运行数据降低了9.5%。

6.结论

通过仿真验证，本文所建立的基于人工蜂群算法的节能操纵优化模型正确，能达到良好的节能优化效果，能较好地解决列车节能运行优化问题，从而验证了人工蜂群算法在降低列车运行能耗方面的有效性。在列车长距离运行过程中，本文将列车简化为单质点模型来进行分析计算，但实际状态非常复杂，机车之间的相互作用力会对列车运行产生影响，因此在后续的研究中可采用多质点的刚性质点链模型来提高建模精度。C