超短期风电功率预测的混合深度学习模型

刘旭丽， 莫毓昌， 吴哲， 严珂

(1. 华侨大学 计算科学福建省高校重点实验室， 福建 泉州 362021； 2.中国计量大学 信息工程学院， 浙江 杭州 310018)

随着经济社会的快速发展，能源的生产和消费也迅速增加.煤炭、石油、天然气等化石能源的大量消耗将导致资源枯竭.因此，调整能源结构和开发利用新能源已成为世界各国经济社会可持续发展的重要战略.风能是一种清洁、可再生、取之不尽的能源.与其他可再生能源相比，风电具有技术成熟、规模化、商业化、便于开发利用、发展前景好等诸多优势.然而，大量风电并入电力系统会产生波动性、间歇性、随机性等问题，给电力系统运行的安全性、稳定性和经济性带来严峻挑战[1].风电的不确定性可以通过需求侧响应管理、备用容量配置优化等方案来解决[2-4].但是，考虑到方案的经济性和可行性，风电功率预测仍然是解决风电不确定性最有效、最经济的方法之一.因此，电力调度部门非常有必要加强对可再生能源进行风能概率预测[5-6]、混合预测[7-9]和太阳能预测[10-12]的研究，以提高功率预测的准确性.准确的风电预测可用于安排发电计划、维护电网平衡，为电网运行和区块管理提供可靠依据，还可以提高风电的渗透性，使风电场在最佳范围内合理运行.

风电预测可以简单地分为超短期预测、短期预测、中期预测和长期预测4个层次.研究者提出物理方法、统计方法、混合方法和学习方法[13]等来解决风力发电预测问题.根据文献[14]，超短期风电功率预测基本采用统计方法.自回归(AR)和差分整合移动平均自回归(ARIMA)等统计模型可以根据大量历史数据预测风电功率.物理方法需要大型计算系统、风电场周围的地形地貌信息和对低层大气的详细描述[15].混合方法是不同方法的组合，例如，统计方法和学习方法的结合.Chang等[16]提出了径向基函数神经网络(RBFNN)和ARIMA的混合模型，该模型兼具统计方法和学习方法的优点，可以处理具有非线性函数的时间序列数据.学习方法也称为黑盒方法，人工神经网络(ANN)、循环神经网络(RNN)、长短期记忆(LSTM)神经网络和时间卷积网络(TCN)等学习方法被广泛应用于风电功率预测[17-20].

随着深度学习模型的广泛应用，本文提出一种基于离散小波变换(DWT)、时间卷积神经网络(TCN)和长短期记忆(LSTM)神经网络的混合深度学习模型.首先，通过DWT将原始功率数据进行分解；然后，利用TCN分别从原始功耗通道和小波分解通道提取时域和频域特征，并进行特征融合；最后，通过LSTM继续提取数据中的长期依赖信息，输入全连接层得出下一时刻的风电功率预测结果.

1 基本概念

1.1 离散小波变换

小波变换是将原始数据与小波基函数和尺度函数进行内积运算的过程.小波变换包括离散小波变换和连续小波变换(CWT).与CWT相比，DWT不仅冗余性好，且重构误差相对CWT较低.因此，采用DWT分解原始风电功率序列.

DWT三级分解，如图1所示.原始信号x[n]进行3次分解后，获得多级频域特征.每次信号分解都同时通过低频通滤波器l[n]和高频通滤波器h[n]的2个分支，从而得到每级的分解系数.

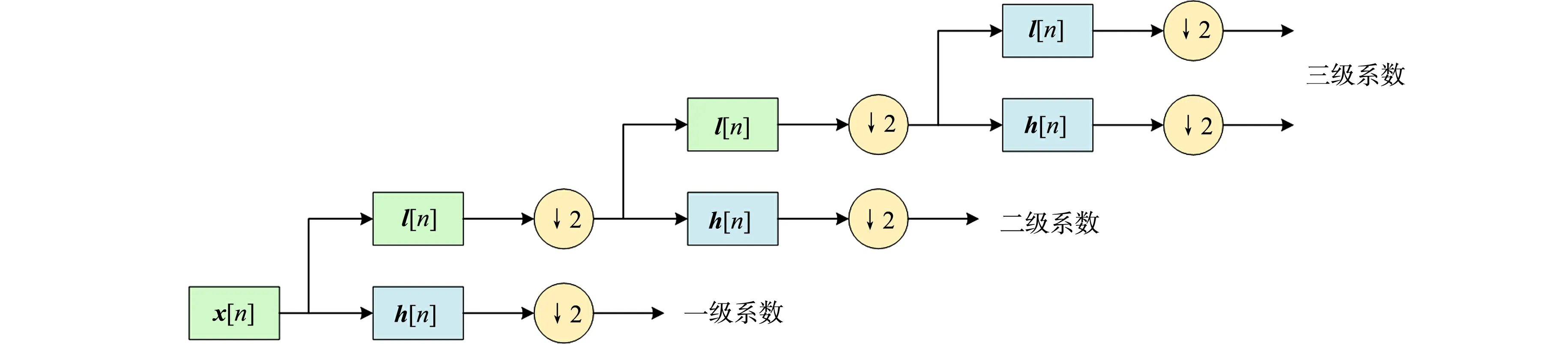
图1 DWT三级分解Fig.1 DWT three-level decomposition

在第1级DWT分解中，原始数据被分解为低频和高频部分，高频部分(细节分量1)保留，低频部分(近似分量1)则继续用于后续分解.重复上述操作2次得到第2，3级多分辨率频域特征：近似分量2和细节分量2；近似分量3和细节分量3，而最终保留的分解分量为细节分量1、细节分量2、细节分量3和近似分量3.

1.2 时间卷积神经网络

卷积神经网络分为一维和二维，卷积神经网络在语音用户界面、自然语言处理和计算机视觉中比较常用.在时间序列预测中，常用时间卷积神经网络进行信息特征提取，TCN使用一维卷积处理单变量时序数据.时间卷积神经网络主要包含卷积和池化操作2个组件，它们通常交替出现在TCN的结构中.二维卷积神经网络(CNN)卷积核大小为k×k，TCN卷积核大小为k×1.卷积神经网络通常使用ReLU作为激活函数.

TCN的卷积过程，如图2所示.输入数据中，部分橙色区域和卷积核对应元素相乘并相加来完成一次卷积计算，经过一次运算后，卷积核按照设定步长继续向后进行同样的运算，最终得到右边卷积运算后的结果，同样多个输入得出多个输出.

图2 TCN的卷积过程Fig.2 Convolution process of TCN

池化操作包括最大、最小和平均池化.最大池化操作表达式为

(1)

TCN的最大池化过程，如图3所示.取左边池化区域中的最大值替换左边区域中的每个元素，进而得到右边对应颜色的池化结果.

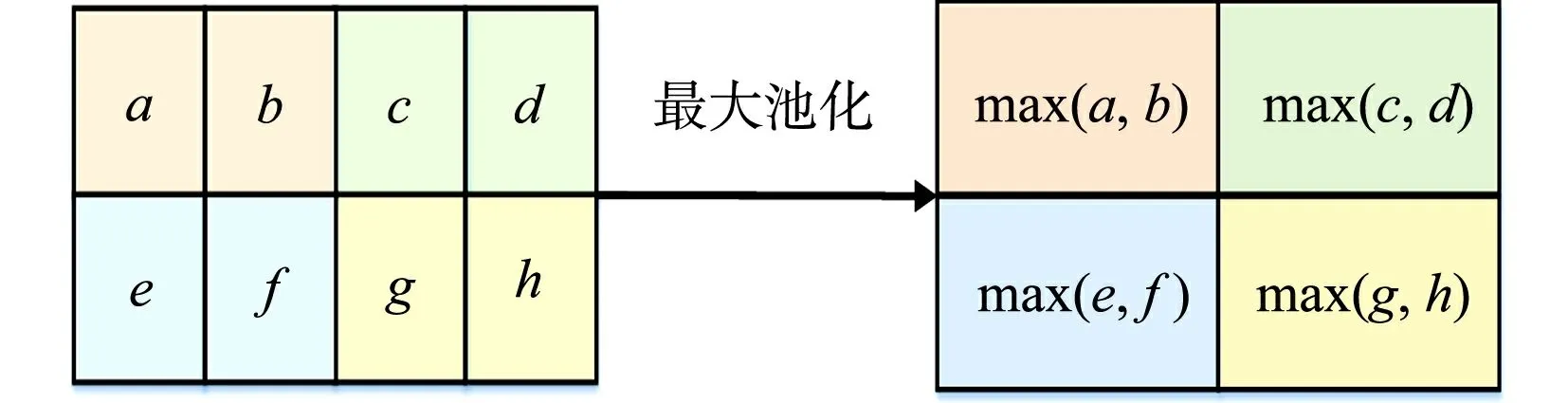
图3 TCN的最大池化过程Fig.3 Max pooling process of TCN

1.3 长短期记忆神经网络

人工神经网络包括前馈神经网络和反馈神经网络.前馈神经网络比较常用的有反向传播神经(BP)网络和CNN，而反馈神经网络常用的包括RNN和LSTM.相对于RNN，LSTM在序列建模方面有一定的优势，具有长时记忆功能，实现起来更简单.除此之外，LSTM还能解决RNN梯度消失和梯度爆炸问题.

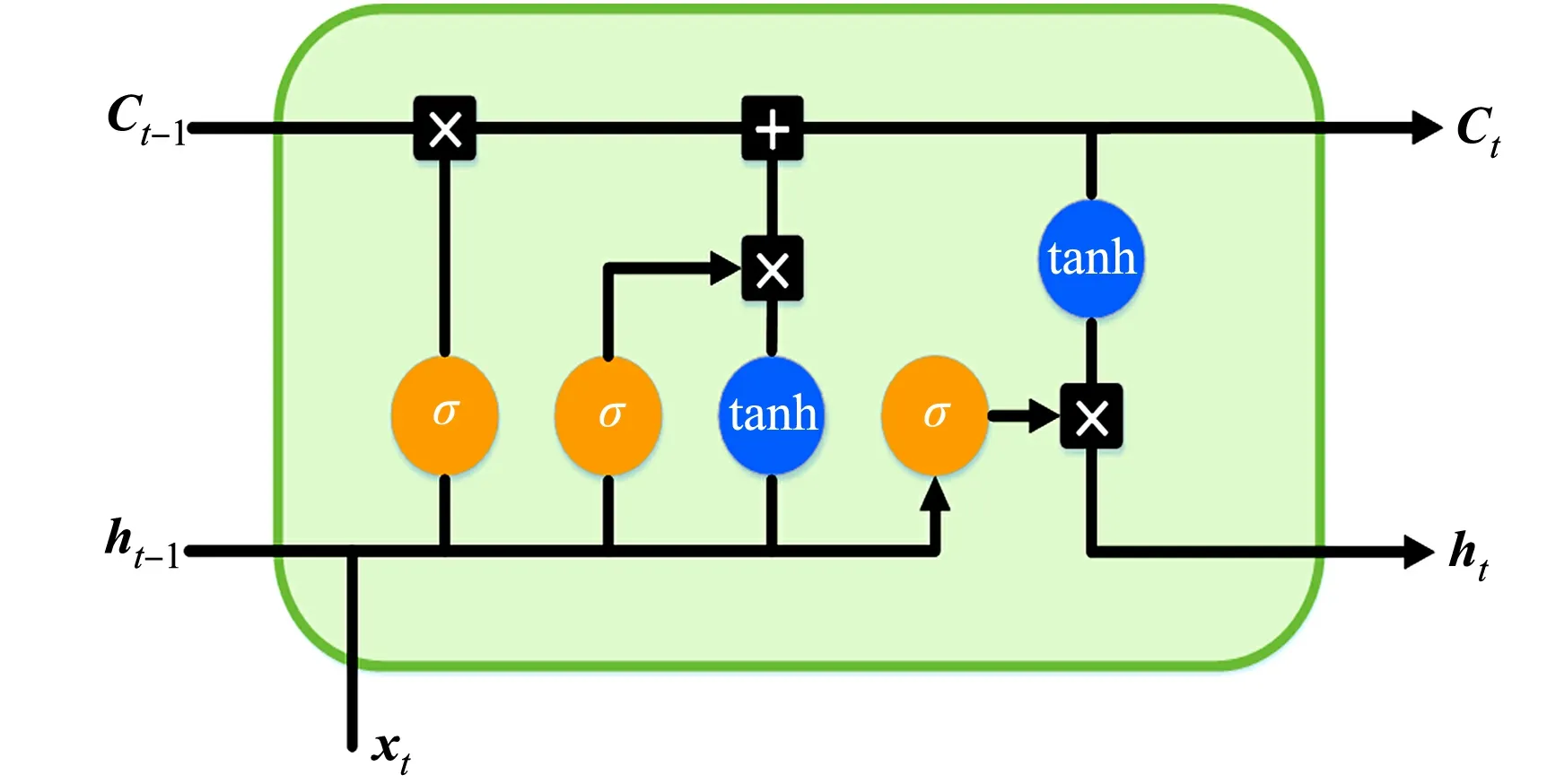
图4 LSTM细胞结构Fig.4 LSTM cell structure

ft=σ(Wf·[ht-1，xt]+bf)，

(2)

it=σ(Wi·[ht-1，xt]+bi)，

(3)

ot=σ(Wo·[ht-1，xt]+bo)，

(4)

(5)

(6)

ht=ot·tanhCt.

(7)

式(2)～(7)中:Wf，Wi，Wo分别为遗忘门、输入门、输出门的权重矩阵；bf，bi，bo分别为遗忘门、输入门和输出门偏置；WC，bC分别为求解当前候选细胞状态的权重矩阵和偏置.

2 DWT-TCN-LSTM模型

超短期风力发电功率预测的混合深度模型(DWT-TCN-LSTM模型)，如图5所示.它包括输入、双通道TCN特征提取、特征融合、LSTM特征提取、输出和更新网络5个过程.其中，TCN特征提取包括时域和频域两个部分，TCN分别从原始功率通道和小波分解通道提取时域和频域特征.

图5 DWT-TCN-LSTM模型Fig.5 DWT-TCN-LSTM model

将原始风电功率数据进行小波分解，经过多次实验对比发现，小波一级分解优于小波二级和三级分解，所以使用小波一级分解将风电功率数据分解为近似分量和细节分量两部分.输入包括原始功率数据和由小波分解得到的功率数据分量.对两部分输入进行数据预处理，首先，选择最大、最小值标准化对数据集进行归一化处理；然后，划分训练集和测试集；最后，通过滑动窗口法得到序列长度为L的时间序列数据，进一步解决原始功率数据维度较低的问题.窗口随时间序列移动，如图6所示.图6中：Input_vector为窗口里的数据组成的向量；target为需要预测的目标值；P为风电功率；t为时间.

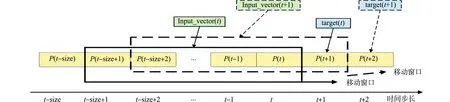
图6 窗口随时间序列移动Fig.6 Window moves with time series

将预处理后的数据输入模型中，数据通过原始功率通道和小波分解通道，利用TCN提取时域和频域特征.利用TCN通过原始功率消耗通道提取数据中的时域隐藏特征，如图5中的绿色虚线框所示，TCN特征提取块由2个一维卷积层组成，使用的激活函数为ReLU，在2个连续的卷积层后加入最大池化层.其中，这2个Conv1D层过滤器个数分别为32和64，过滤器大小都为3，第1个TCN层用来提取数据中的局部隐藏特征，第2个TCN层则用于全局隐藏特征的提取.在卷积运算之后，使用1个最大池化层进一步加快网络训练速度.卷积操作非常有效，在深度学习框架中，堆积多个卷积层使初始层能够学习应用输入中的低级特征.作为卷积层输出的特征图有1个限制，即它会跟踪输入中特征的精确位置，这意味着输入中特征位置的微小移动将导致不同的特征图.通常在卷积层后添加1个池化层，以减轻生成的特征图不变性的限制，而激活函数则用于增强模型学习复杂结构的能力.在模型中，最大池化层是一种下采样方案，可将特征图的空间维度降低2倍，从而降低整体计算负载.ReLU激活函数对梯度消失问题具有弹性，已被研究人员广泛实施，使网络更易于训练.

小波分解通道用来获取频域隐藏特征，如图5中的红色虚线框所示，每个分支都连接2个一维卷积层，在分支汇合处连接合并层.DWT分解后的细节分量和近似分量分别输入2个分支中，以提取数据中的频域隐藏特征.2个Conv1D层的过滤器个数分别为32和64，过滤器大小都为3.最后，合并由TCN从小波分解通道提取的多个频域特征，进一步获取频域融合特征.

在TCN提取操作后分别获取数据的时域特征和频域融合特征，再通过合并层的使用获得数据的时频域融合特征.为了进一步提取数据中具有长期依赖关系的信息，采用带有节点为80的LSTM层来提取数据的长期依赖特征，从而获得具有长期依赖性的时频域融合特征.

在任何深度学习模型的开发中，dropout层提供了一种很新颖的方法来缓解过拟合问题.该层包括随机选择神经元，并在训练过程中停用其中一些神经元.在平面化层和全连接层之间加入1个dropout层，以防止过度拟合.序列学习块的输出连接到1个dropout层，然后是一个全连接层以产生最终输出.

在训练过程中，使用小批量梯度下降算法使真实值与预测值之间的平均绝对误差(MAE)达到最小值来更新网络参数.此外，采用优化器Adam找到最佳的收敛路径，全连接层的激活函数采用sigmoid.

3 实验结果与分析

3.1 实验数据

对风电功率数据进行特征分析，风电功率数据曲线，如图7所示.图7中：n为测试集数据数.图7是从总数据中随机提取的500个风电功率数据.由图7可知：风电功率数据存在不稳定性，尤其是连续低值问题.

图7 风电功率数据曲线Fig.7 Wind power data curve

从GitHub网站上下载风力发电功率公开数据集，数据起始时间是2017年1月1日至2017年12月31日.数据的测量从早到晚24 h不间断，测量间隔时间为15 min.训练集和测试集数据数，如表1所示.表1中：N为总数据数.分别进行时间间隔(Δt)为15，30，60 min的预测实验.将80%的原始数据作为训练集，其中5%进行验证，剩余20%的原始数据作为测试集.

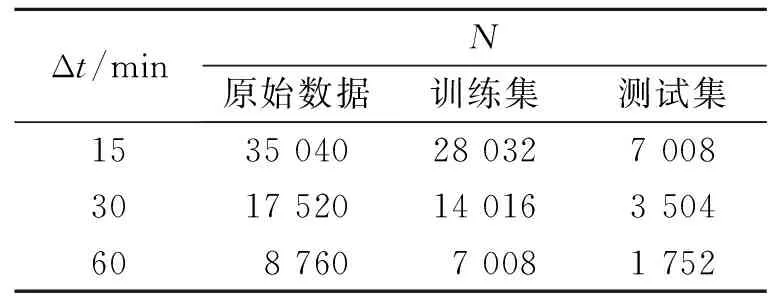
表1 训练集和测试集数据Tab.1 Training set and test set data

3.3 对比模型

将文中模型(DWT-TCN-LSTM模型)与ARIMA模型、支持向量回归(SVR)模型、LSTM模型和卷积长短期记忆(TCN-LSTM)混合模型进行对比.ARIMA是时间序列预测分析方法之一，是统计方法中常用的时序模型，其缺点是要求时序数据是稳定的，本质上只能预测线性关系，不能预测非线性关系，对不稳定的风电功率数据，预测效果较差.SVR 是机器学习中主要用来处理回归问题的模型.LSTM是深度学习中主要用来时序预测的模型，作为单一的深度模型提取的数据特征有限，相对于TCN-LSTM，LSTM模型的性能较差.使用TCN-LSTM模型与文中模型作对比，进一步说明小波分解对TCN-LSTM模型的影响.

3.2 评价指标

采用对称平均绝对百分比误差(SMAPE)、均方根误差(RMSE)和平均绝对误差(MAE)3个评价指标对模型的性能进行评价，其计算式分别为

(8)

(9)

(10)

式(8)～(10)中:xi为实际值；yi为预测值.

3.4 预测结果分析

为了考察文中模型在不同时间间隔(15，30，60 min)的预测性能，与其他4个模型进行对比.不同时间间隔内，5个模型在3个不同时间间隔上的RMSE，MAE和SMAPE比较，分别如表2～4所示.

表2 5个模型在3个不同时间间隔上的RMSE比较Tab.2 Comparison of RMSE of five models at three different time intervals

表3 5个模型在3个不同时间间隔上的MAE比较Tab.3 Comparison of MAE of five models at three different time intervals

表4 5个模型在3个不同时间间隔上的SMAPE比较Tab.4 Comparison of SMAPE of five models at three different time intervals

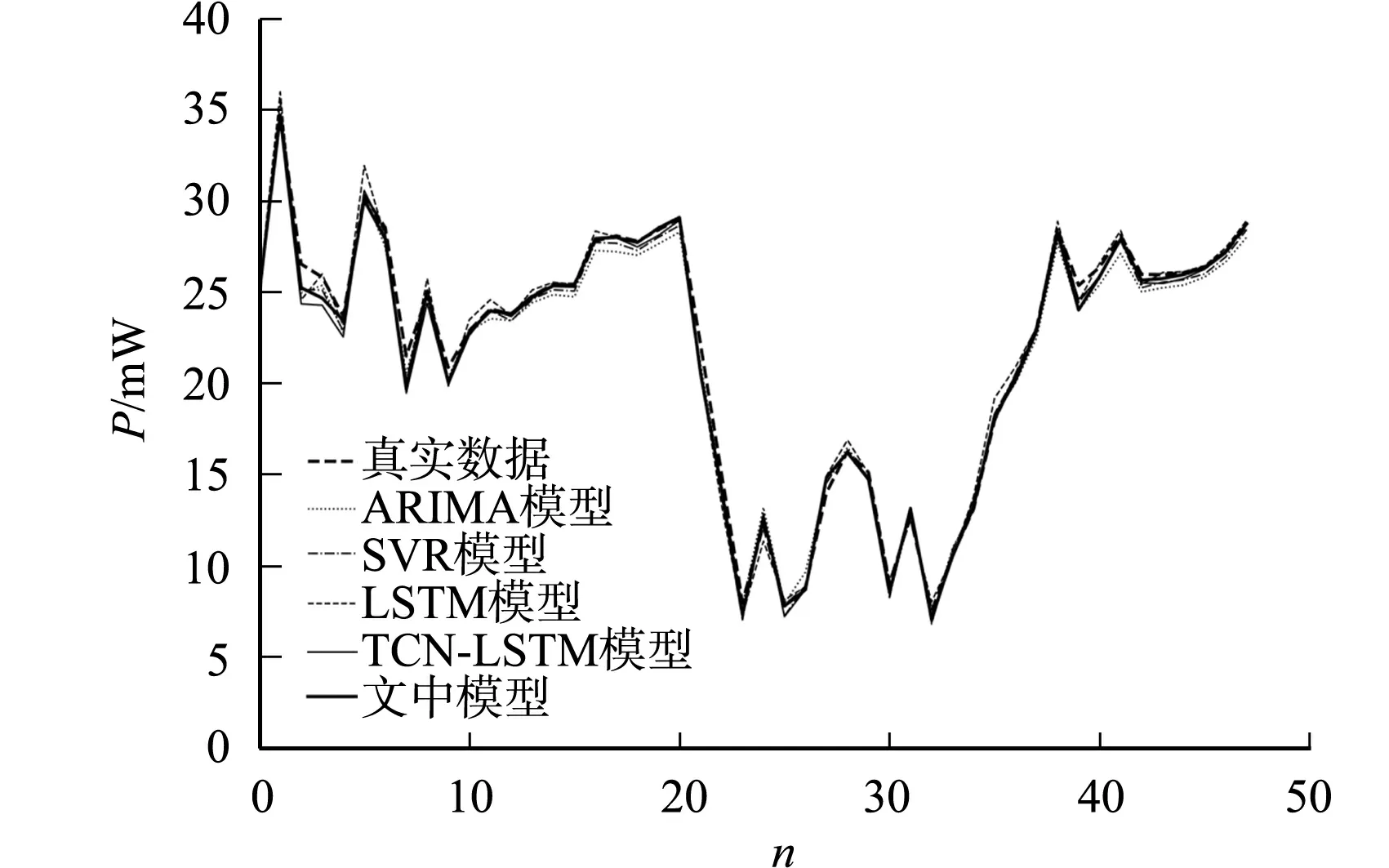
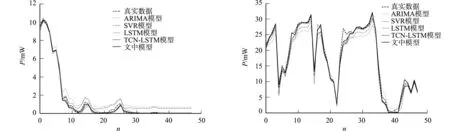
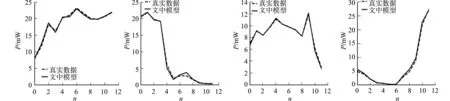
RMSE侧重刻画风力发电功率峰值的预测误差，模型峰值的预测效果越差，则该模型的RMSE值就越大；RMSE值越小，说明模型的预测效果越好.由表2可知：文中模型在3个不同时间间隔的表现均为最优；从3个时间间隔的预测结果的平均值来看，RMSE值排序为文中模型

MAE着重刻画风力发电功率平稳状态时的预测误差，MAE值越小，说明预测效果越好.由表3可知：文中模型在平稳状态的预测效果最好，从3个时间间隔预测结果的平均值来看，MAE值的排序为文中模型

SMAPE刻画了风力发电功率的整体预测效果，也是评价模型预测效果的主要依据，SMAPE值越小，说明预测效果越好.由表4可知：在时间间隔为30，60 min时，文中模型表现均为最优，在时间间隔为15 min时，文中模型和TCN-LSTM模型的预测效果相同，优于其他3个模型；从3个时间间隔预测结果的平均值来看，SMAPE值的排序为文中模型

文中模型使用DWT扩充数据维度，以提升TCN-LSTM模型的预测精度，为了验证文中模型的预测效果是否比TCN-LSTM模型有提升，使用SMAPE作为评价标准评估两种方法的预测性能.对比文中模型和TCN-LSTM模型在不同时间间隔数据集上的SMAPE值可知，文中模型在不同时间间隔数据集上的预测性能均有提升，相比原有的TCN-LSTM模型，在时间间隔为30，60 min数据集上的SMAPE值分别提升了18.09%和8.57%.说明使用离散小波变换扩增功率数据特征对提升超短期风力发电功率预测精度具有显著效果，证明了文中模型的有效性.

3.5 预测结果曲线图

DWT-TCN-LSTM模型代码通过Keras 2.3.1版实现.DWT使用一级分解，TCN使用2层卷积和1层池化，LSTM层使用80个隐藏单元，而全连接层使用1个隐藏单元用于输出预测结果.通过随机初始化重建DWT-TCN-LSTM模型，重复实验10次，将DWT-TCN-LSTM，TCN-LSTM，LSTM，SVR和ARIMA模型在时间间隔分别为15，30，60 min的预测结果进行比较，结果如图8所示.

(a) Δt=15 min

(b) Δt=30 min (c) Δt=60 min图8 5个模型在时间间隔为15，30，60 min的预测曲线Fig.8 Prediction curves of five models at time intervals of 15， 30， and 60 minutes

由图8可知：时间间隔为15 min时，5个模型的预测曲线差距不明显，总体来看，文中模型曲线拟合较好；时间间隔为30 min时，当真实数据曲线数值较低且波动较小时，文中模型表现最好，LSTM和TCN-LSTM模型次之，ARIMA和SVR模型的预测效果较差.由于在无风情况下，风力发电功率存在连续0值，用平均值填充并不能取得好的预测效果，因此，保留了连续0值，而文中模型对连续低值的预测效果比其他模型更好.这也验证了文中模型在3个时间间隔内的MAE表现较好的结论.当时间间隔为60 min时，与LSTM，TCN-LSTM模型和文中模型相比，ARIMA和SVR模型的预测曲线拟合较差，LSTM模型虽然表现良好，但是在峰值和低值预测方面仍然没有文中模型的预测性能好.总体来看，无论是波动较大的数据还是平稳性较好的数据，相对于其他模型，文中模型的预测曲线与实际曲线更为接近.

文中模型预测曲线和真实数据曲线的对比，如图9所示.图9是从时间间隔为15，30，60 min的数据中随机抽取的4组数据绘制的曲线.

(a) Δt=15 min

(b) Δt=30 min

(c) Δt=60 min图9 文中模型预测曲线和真实数据曲线的对比Fig.9 Comparison between prediction curves of proposed model with real data curves

由图9可知：当时间间隔为15，30 min时，文中模型的预测曲线与真实曲线较为接近；当时间间隔为60 min时，随着时间间隔的增大，文中模型的预测曲线逐渐偏离实际曲线，但偏差不大；在不同的时间间隔内，文中模型对连续低值的预测效果表现较好，进一步证实了之前的结论.

4 结论

风力发电功率预测是解决风电不确定性最有效、最经济的方法之一.提出一种基于离散小波变换(DWT)，时间卷积网络(TCN)和长短期记忆(LSTM)神经网络的时频域融合深度学习模型.与TCN-LSTM模型不同，DWT-TCN-LSTM模型利用TCN通过小波分解通道提取频域特征，再利用LSTM学习长期依赖信息，提高了TCN-LSTM模型的预测能力.

通过实验对比，得出在15，30，60 min时间间隔内，ARIMA，SVR，LSTM，TCN-LSTM和DWT-TCN-LSTM模型的3个误差评价指标及预测曲线对比图.结果表明：与其他4个模型相比，DWT-TCN-LSTM模型的预测能力具有明显的优势.

未来的研究工作将继续寻找新的模型应用到风力发电功率预测中.