基于PSO-BP的胶结充填体强度预测研究

石 劲 杜澳宇 王西兵 卢 骏 兰建强 郑先伟

（1.武钢资源集团程潮矿业有限公司；2.武汉科技大学资源与环境工程学院）

充填采矿法是实现绿色矿山建设的最好工艺方法，因其能有效控制地压和地表沉降而逐渐被推广应用[1]，特别是在两步骤回采中充填体充当人工矿柱支撑采场顶板，其稳定性对矿柱的安全回采至关重要[2]。为快捷、准确地确定胶结充填体的强度，国内外学者针对胶结充填体的强度预测方法进行了广泛的研究。郑迪等[3]通过试验研究胶结充填体灰砂比和浓度对强度的影响规律；韩斌等[4]通过正交试验开展室内试验，探究出胶结充填体强度和料浆浓度及灰砂比的规律方程；付自国等[5]基于63组配合比强度试验，建立了超细尾砂胶结充填体双变量强度计算模型。随着现代化无损检测技术的发展，超声波以其传播距离大、能量损失小、穿透力强、使用快捷简单等特点得到了广泛的应用。国内外学者利用超声波检测技术对充填体强度预测进行了相关研究，Cao等[6]开展了单轴压缩和超声波监测试，探讨了分层胶结粗尾砂充填体单轴抗压强度和超声脉冲速度之间的关系；穆光慈等[7]建立了基于超声波脉冲速度的胶结充填体单轴抗压强度预测模型，发现超声波脉冲速度与单轴抗压强度之间存在明显的二项式关系；程爱平等[8]基于波速—密度双参数预测指标构建了胶结充填体强度预测模型，对比分析得出所构建的强度预测模型拟合结果良好。上述研究中，胶结充填体强度的获取主要依据室内试验，该方法对胶结充填体试样尺寸、表面平整度、加载速度等条件要求较高，很难在工程现场进行，且时效性和经济性较差。

随着人工智能的发展，一些优秀的机器学习算法，特别是神经网络被广泛的应用于分类预测等领域。作为AI 算法的BP（误差反向传播）神经网络，因易与其他算法结合而被用于预测胶结充填体的强度。徐淼斐等[9]对充填体的固体质量分数和试件形态的影响规律进行了灰色—关联度分析，建立了充填体BP 神经网络强度预测模型；胡凡等[10]利用BP 神经网络模型对某矿山的四种尾砂材料浇筑的充填体试样强度进行预测，总体预测效果良好；刘团结等[11]建立了胶结充填体优化BP 强度预测模型，建立的预测模型收敛速度快而且精度高。上述研究基于BP神经网络预测了胶结充填体的强度，但由于数据预测受数据集大小以及神经网络算法本身特性的影响—数据集过大导致迭代时间过长，数据集偏小导致预测结果不稳定，以及单一神经网络预测易陷入局部最优或根本没有达到局部最优就停止迭代，直接导致BP预测的拟合效果不理想。

基于此，本研究采用了粒子群算法（PSO）对传统BP 神经网络的初始权值进行优化，并基于正交试验数据建立了PSO-BP 神经网络预测模型，对尾砂胶结充填体的强度进行预测，并结合正交试验结果验证模型的可靠性。

1 改进的PSO-BP的神经网络预测模型

1.1 BP神经网络模型

BP神经网络算法原理是将神经网络的预测值与实际值的误差等效更新为权值和阈值。设样本对（X,Y），X =[x1,x2,...,xn]，Y =[y1,y2,...,yn]，隐含层神经可表示为 S =[s1,s2,...,sn]，设 wij、wjk为输入层与隐含层间的网络权值。θi为隐含层神经的阈值，θj为输出层神经元的阈值，则输出层神经元、隐含层神经元输出分别为

式中，f为隐含层传递函数；g为输出层的传递函数。

则训练误差E为

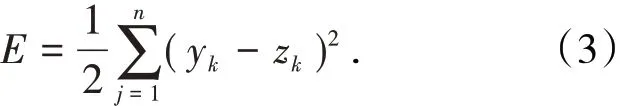
假设wsp为网络的连接权值，则权值修正Δwsp为

通过权值调整公式得到调整后的权值为

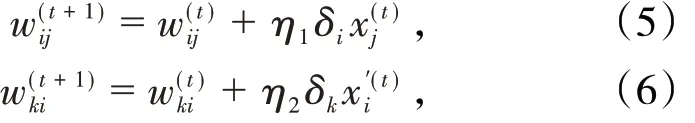
其中，η1、η2分别为隐含层和输出层的学习步长，t 则代表迭代的次数，式中δk、δi分别为

在BP 神经网络中包含输入层X =[x1,x2,...,xn]、中间层(隐含层)以及输出层Y =[y1,y2,...,yn]，输入数据之后数据根据相应的权值进行运算，通过对比输出与测试集合的偏差更新权值，进行学习与迭代，使神经网络的权阈值进行更新，同时根据误差反馈原理，将误差反馈到输入层，不断更新权阈值。BP神经网络结构见图1。

1.2 粒子群算法（PSO）

粒子群优化算法是Eberhart和Kennedy提出的一种高效并行优化方法，借鉴鸟群的种群行为通过赋予无质量粒子位置与速度并根据相互传递的信息朝着最优解移动。它不依赖于所求问题的具体领域，而是直接以决策变量的编码作为运算对象，以适应度函数值为搜索目标，且可以同时使用多个搜索点的信息，适用于求解一些非线性、不可微、多目标的复杂优化问题，常应用于神经网络，遗传算法等。

设在一个D维的目标搜索空间中，有N个粒子组成一个群落，其中第i 个粒子代表一个D 维向量xi=(xi1,xi2,...,xid)，即第i 个粒子在D 维搜索空间中的位置，而每个粒子的位置x 为一个潜在的解。将x 代入一个目标函数即可算出其适应值，根据适应值的大小衡量x是否为所要求解的最优解。

第i 个粒子的“飞翔”速度也是一个D 维向量，记为vi=(vi1,vi2,...,vid)，记第i 个粒子到第h 次迭代为止搜索到的最优位置为pi=( pi1,pi2,...,pid)，整个粒子群到第h 次迭代为止搜索到的最优位置为pgd=( pi1,pi2,...,pid)。算法的基本公式如下：

1.3 PSO-BP神经网络预测模型构建

基于上文中提到的神经网络存在初始权值、阈值过于随机，导致计算时间长的问题，采用粒子群(PSO)算法对其初始权值、阈值进行优化，从而减少计算权值耗费的时间。具体流程如下：

（1）初始化粒子群包括参数设置：粒子种群为100 个，学习因子c1=c2=2.0，惯性权重设置wmax=0.9，wmin=0.4，粒子初始化速度为[-1,1]。

（2）设置BP 神经网络预测误差作为粒子种群的适应度函数。

（3）计算粒子种群的适应度，比较得出最佳位置，并将最佳位置赋予给全体种群。

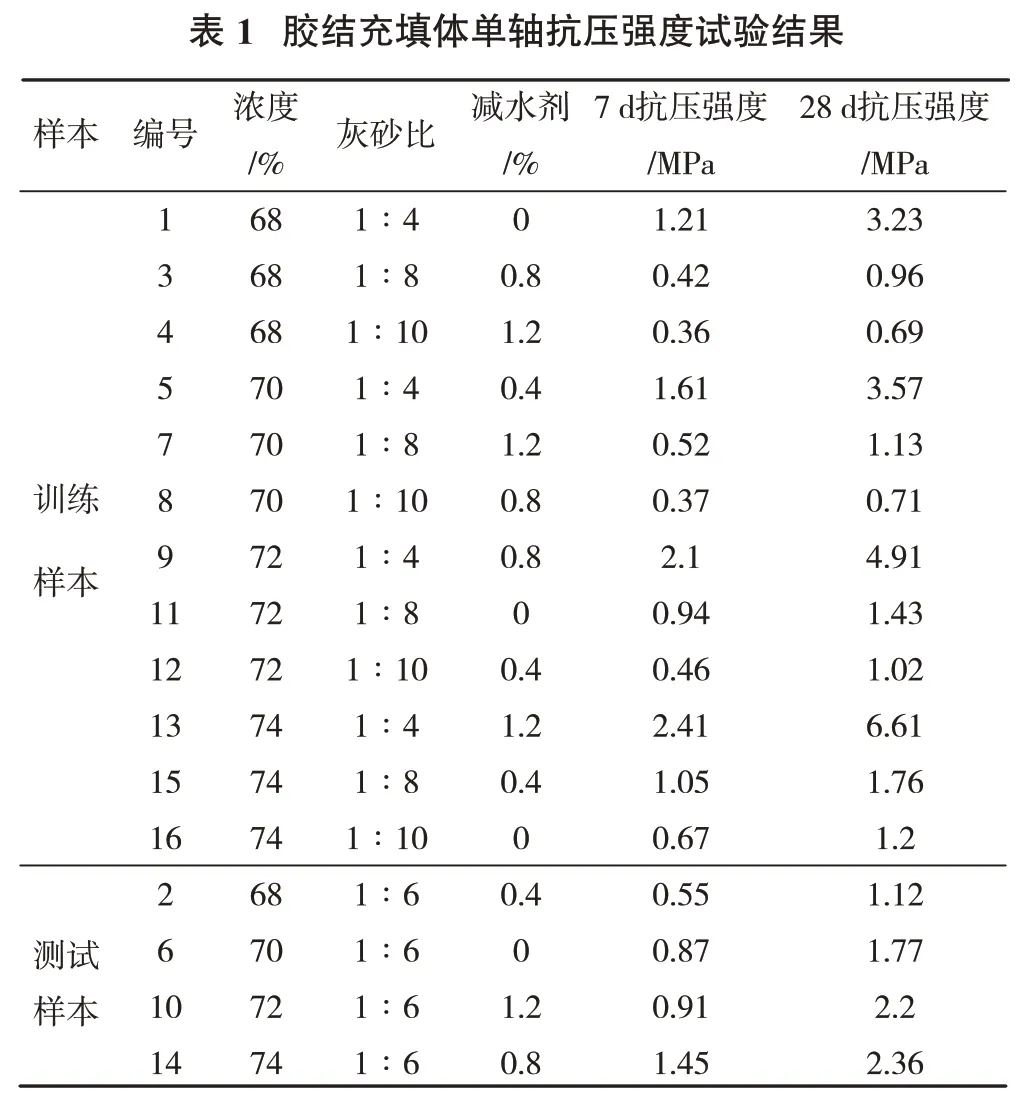
（4）得到通过PSO 优化后的权值，进而通过得到的数据特征输入，得到预测输出。其中BP 神经网络参数选取为其中神经元个数设为10，最大迭代次数设置为1 000，学习率设置为0.1。具体流程如图2。结充填体强度预测模型，与本文的预测结果进行对比分析。基于PSO-BP 神经网络预测模型以及对实验数据分析建立相应的训练样本和测试样本见表1，本研究利用PSO-BP 神经网络预测模型计算出的预测值及BP 预测值见表2。PSO-BP 算法对充填体强度的预测结果与试验结果最高精度达到了99.97%，平均相对误差为0.77%，相比BP 神经网络的平均相对误差4.19%，预测精度更高，PSO-BP 算法为胶结充填体强度预测提供一种切实可行的方法。

2 工程应用

为验证本文提出的基于PSO-BP 神经网络算法的胶结充填体强度预测模型的可靠性，结合刘恒亮等[12]建立的基于正交试验的BP 神经网络全尾砂胶

?

?

3 结 论

（1）对于BP 神经网络已陷入局部最优的缺点采用粒子群算法进行优化，通过训练、验证以及测试等一系列的运算后发现PSO-BP 神经网络预测模型预测精度高于BP神经网络预测模型，并且稳定性较高。

（2）预测结果与试验结果整体更平稳，BP神经网络预测平均相对误差为4.19%，PSO-BP 预测平均相对误差为0.77%；7 d均方根误差为0.012，相对降低了0.034；28 d 均方根误差为 0.018，相对降低了 0.293，PSO-BP 模型相对于原始模型效果更好，算法比BP算法预测精度更高，平均相对误差降低了3.42%，PSO-BP算法预测更加可靠。