基于长度约束的网壳结构形态创建方法

张学玲

（中铁建设集团有限公司，北京 100040）

引言

西班牙建筑师安东尼·高迪和瑞士结构师海因茨·伊斯勒利用“逆吊实验法”设计了多项“薄而刚”的大型薄壳结构。随后对索、膜等柔性结构的建筑形态上出现多种试验方法，如“皂泡法”“湿丝线模型法”和“干丝线模型法”等。实验方法思路简单、直接，给定的原始形状上施加外力可以得出较合理的结构形状。但对复杂的建筑项目来说，特别是探讨多种方案时，时间上、制作细节、费用上不经济，而且缩放过程中很难保证精度。随着计算机效率的迅速提高与数值理论技术的发展，数值计算方法逐渐取代实验方法，已出现了“力密度法”“动力松弛法”“有限元法”“感度分析法”等多种数值方法。这些方法在索、膜等柔性结构找形与拉压结构形状确定问题中开拓了新的思路，提供了新的方法，但要满足建筑的错综复杂要求仍需要进一步的完善。

本文以杆系结构作为研究对象，提出以结构与机构互换方式，创构出受力合理结构的杆系结构形态的方法。该方法根据杆件长度不变的限制条件推导出“移形方程”，确定机构可能位移方向。利用机构势能关于节点坐标参数微分的特性逐步修正机构形状，得出势能最小化的稳定平衡机构形状，最终将机构转换成结构。文中通过算例考察了机构形状变化过程中的势能的变化规律、所对应结构的形状与受力性能变化规律，总结了方法的特点，验证了方法的实用性[1]。

一、方法的建立

1．机构移形方程的建立

机构在外力作用下改变原来的状态往自平衡状态演变，在这演变过程中机构状态的移动近似于刚体的移动，可以以杆件组总长度不变为条件建立“机构移形”方程。

2．机构势能最小化

将结构转换成机构后，机构改变原有状态在某一新状态下自行停留，这现象从能量角度来看，机构改变状态达到势能最小状态的一种结果，而其改变状态过程是机构自行演变的过程。机构在不稳定状态往稳定状态过程中，机构的势能逐步变小[2]。

二、数值算例

1．某工程天窗的网格结构优化示例

以某实际工程天窗的网格结构优化为例。图1a所示为21.2m×2.9m的矩形内的初始设计方案。将以铰接代替各构件的刚接，结构将转换成机构。初始机构四周节点设定为固定铰支座。设定与实际工况方向相反的节点荷载，本算例中，节点荷载大小为1.0kN，方向为竖直向上。图1b所示为机构达到平衡状态时的形状，即处于无弯矩平衡状态时的形状，将此机构的所有节点转化为刚接，机构转化为结构。整体看，优化前后形状变化并不大，图1c所示为结构某一截面处优化前后对比图，优化前结构横截面为圆弧，优化后更接近悬链线[3]。

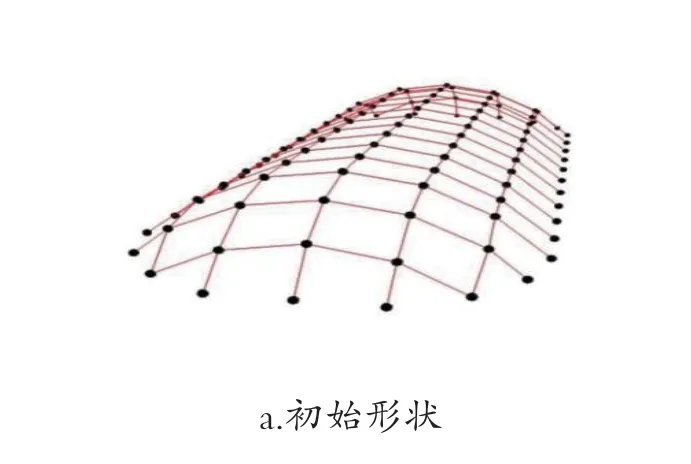
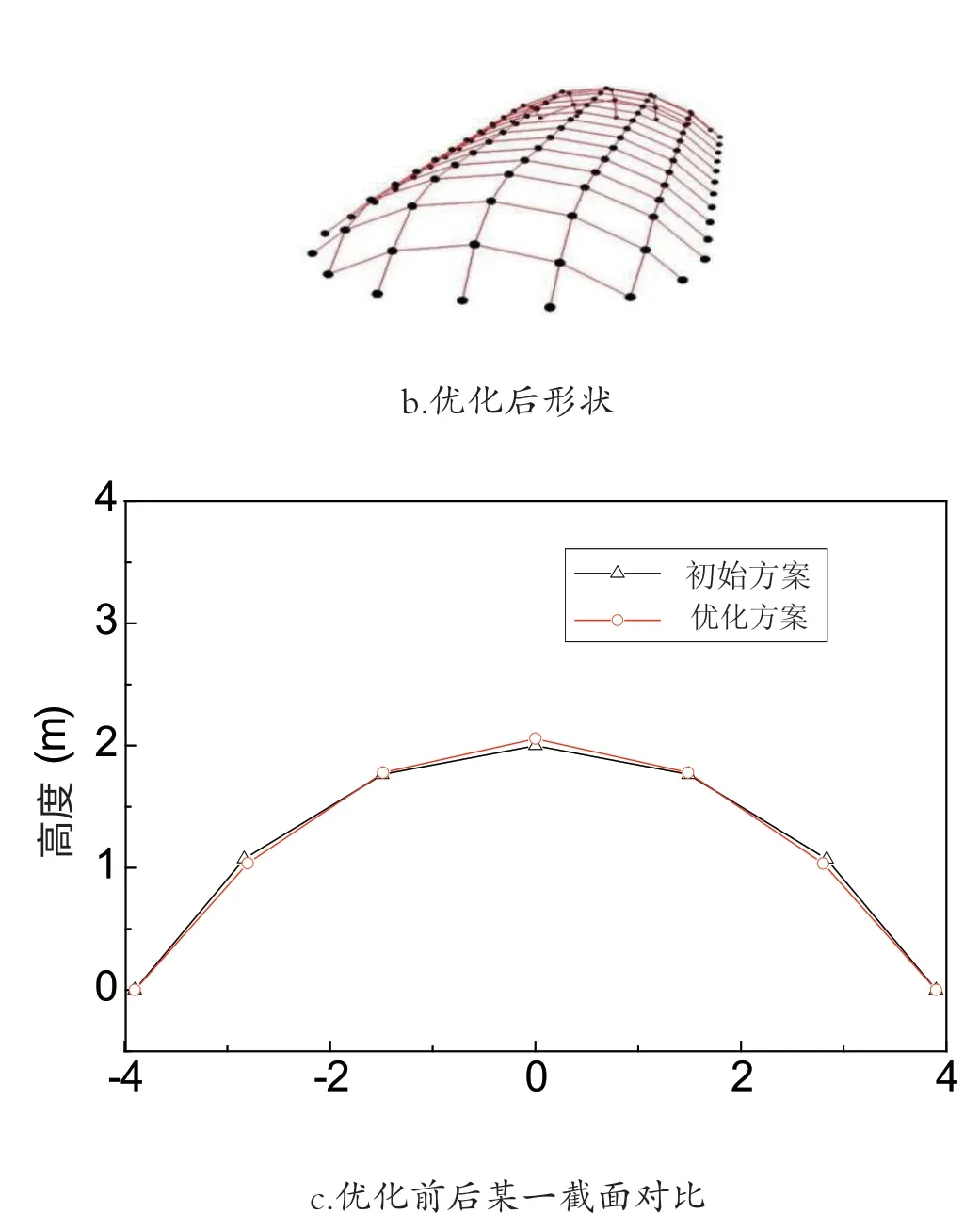
图1 某项目天窗网格结构形状优化

图2所示为机构在形状演变过程中势能增量的变化情况，可知机构势能变化由快变慢并最终收敛于零，在整个机构的变化过程中，所有构件均为刚体，故优化前后构件的长度保持一致，仍然可以采用原设计的基本构件进行施工。

对比优化前后结构力学性能的变化，采用商业有限元软件对初始方案中的结构与优化后的结构进行了力学性能分析。在有限元分析中，节点荷载为1kN，方向竖直向下，所有构件的规格为Φ60×3，弹性模量为200GPa，泊松比为0.3。重点考察优化前后结构内力分布情况的变化，包括结构的最大/平均弯矩、最大/平均轴力，应变能，节点位移。图2展示了优化前后结构在给定荷载下的位移云图，其中位移放大400倍。将对比结果列于表1中，由表中数据，结构的应变能降低了47.5%，最大弯矩与平均弯矩分别降低了81.7%和89.8%，轴力变化不大。原结构方案所有杆件总长度为234.9877356m，优化后结构所有杆件总长度为234.9876749m。由此可知结构的形状变化不大，钢材用量不变的条件下，结构整体的力学性能得到了很大的改善。在给定荷载下，结构形态更加合理[4]。

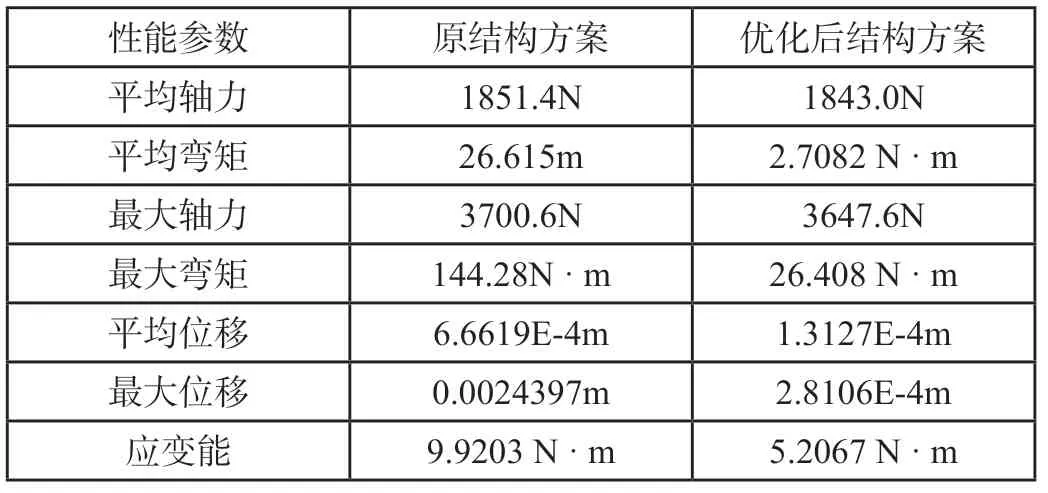
表1 优化前后结构受力性能

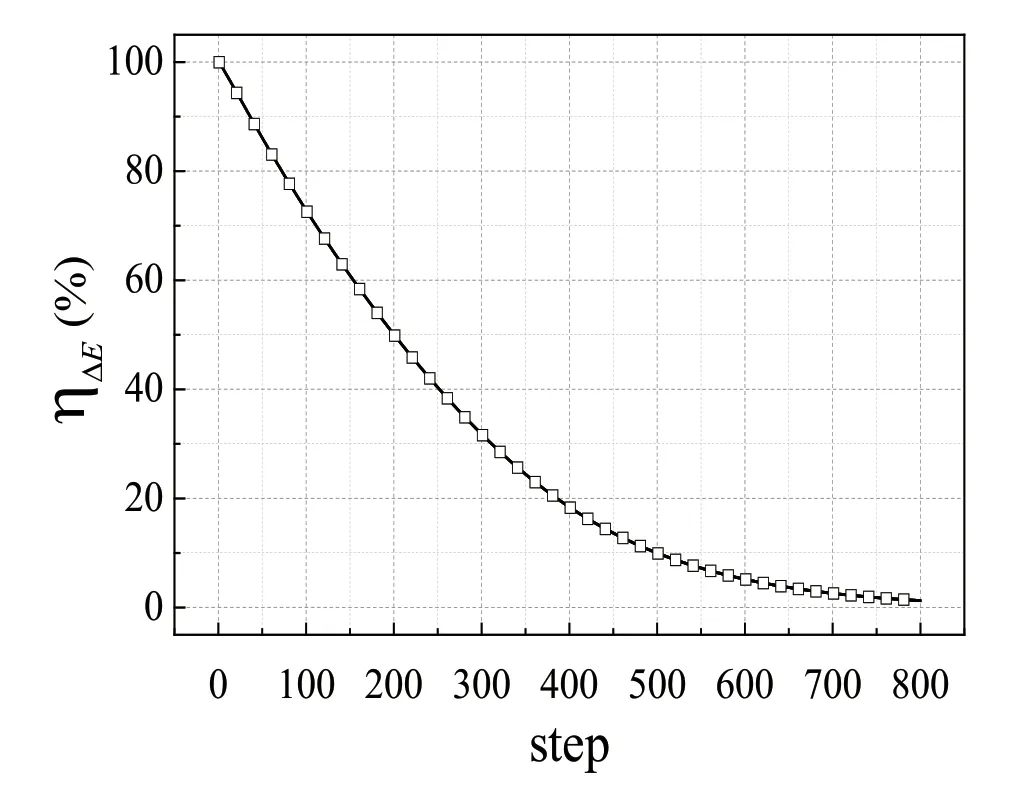
图2 机构势能增量的变化

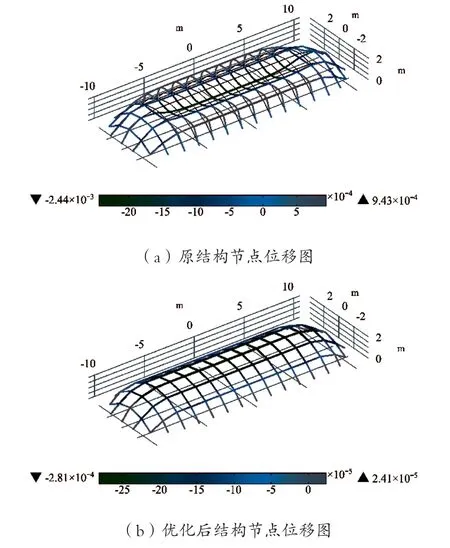
图3 结构位移云图

2．六边形自由曲面网格结构优化示例

在294.5m×160.0m矩形设计域内设置如图4-a的六边形网格初始结构平面与支座位置，根据建筑要求确定初始结构高度与形状。各杆件采用了直径为5.0cm壁厚1.5cm的圆钢管，在各节点上设定了Fd=10.0kN的竖向荷载。

为得出受压结构将实际节点荷载改成方向相反的竖直向上的荷载，并将所有初始结构刚接转换成铰接，结构转换成机构。图4-c和图4-d为所提出的方法创构出的最终结构平面与立面形状。从图中可以看出，最终结构与形状较初始结构相比有了明显的变化。在平面图上的原正规正六边形，不同程度转变成不正规得六边形，落在直线上无支座边界点呈现出抛物线。从立面图上看，中部凸形曲面加大宽度，两侧低凸形曲面与中部连接处得到了高度的调整，整个结构呈现出更加饱满圆滑的三个抛物面，而且平直无支座边界在立面上也形成拱形开口。从初始与最终机构平立面图上不难发现，原来的机构达到“自然平衡状态”时，形状上发生较大的变化，体现出了形状停留状态的力的分布特性。机构由“不平衡状态”达到“自然平衡状态”过程中，恢复实际作用方向荷载时所对应的结构受力性能的变化特性。可以看出机构势能增量，开始变化激烈随后继续放慢速度下降最终趋于零，机构接近稳定平衡状态。每步机构形状所对应的结构应变能也一样，开始变化激烈随后缓慢减少达到初始结构的4%左右时收敛，表明结构的刚度得到了很大的改善[5]。而弯矩变化也很明显，机构达到平衡状态时所对应结构的平均弯矩接近零，最大弯矩也减少到初始结构的20%左右，而平均轴力变化并不大只有减少到82%左右。虽然机构转变成结构以后必定产生弯矩，但其值很小，已经近乎成为纯压结构。再次表明本文提出的方法所得到的结构以轴力为主方式传递荷载的良好结构。该方法约束杆件长度，由于数值计算误差会造成的长度发生一定变化，其中杆件长度变化相对于初始长度的最大值仅为0.3%，由此可知本文方法能够很好地约束单元长度。

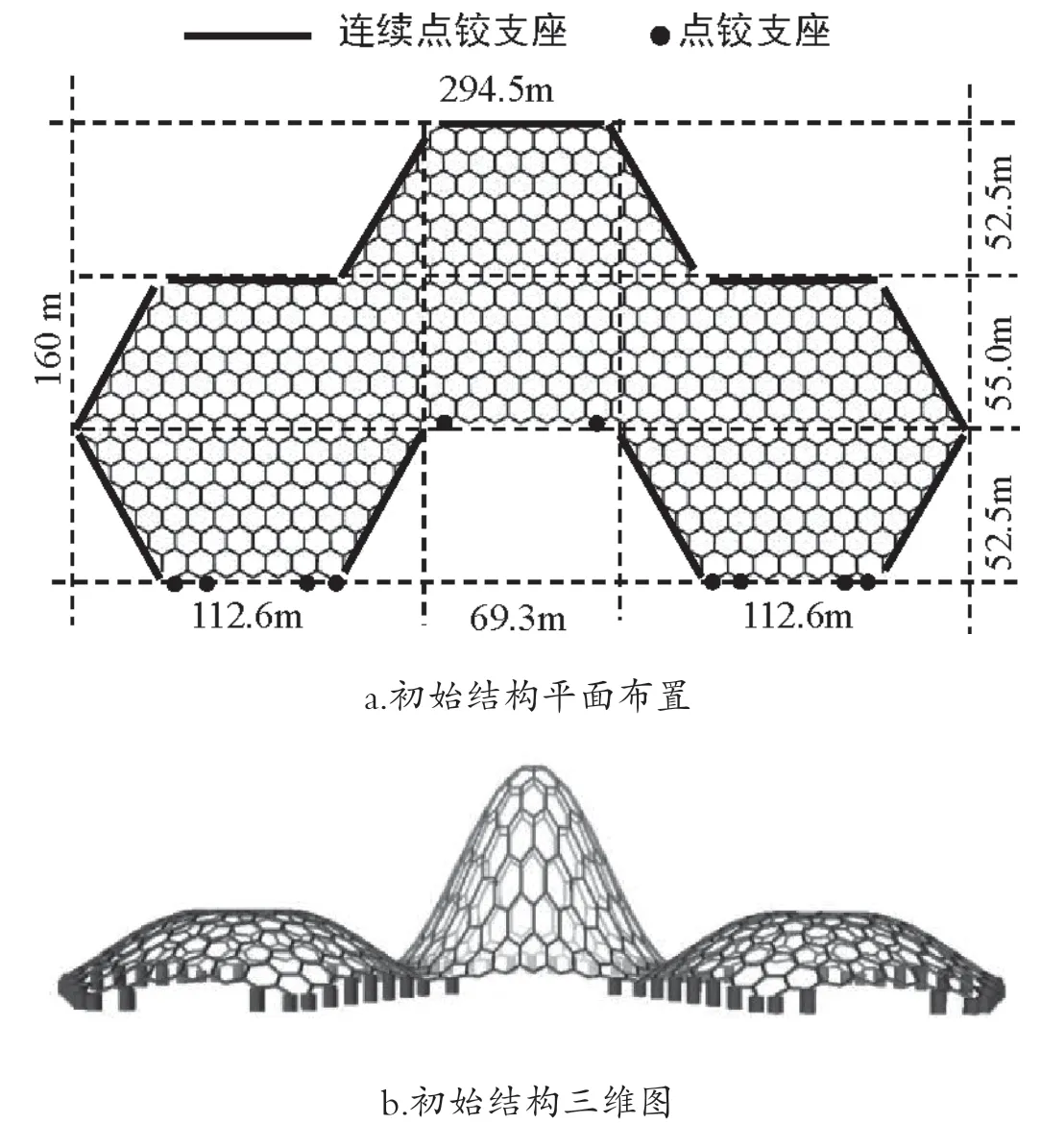
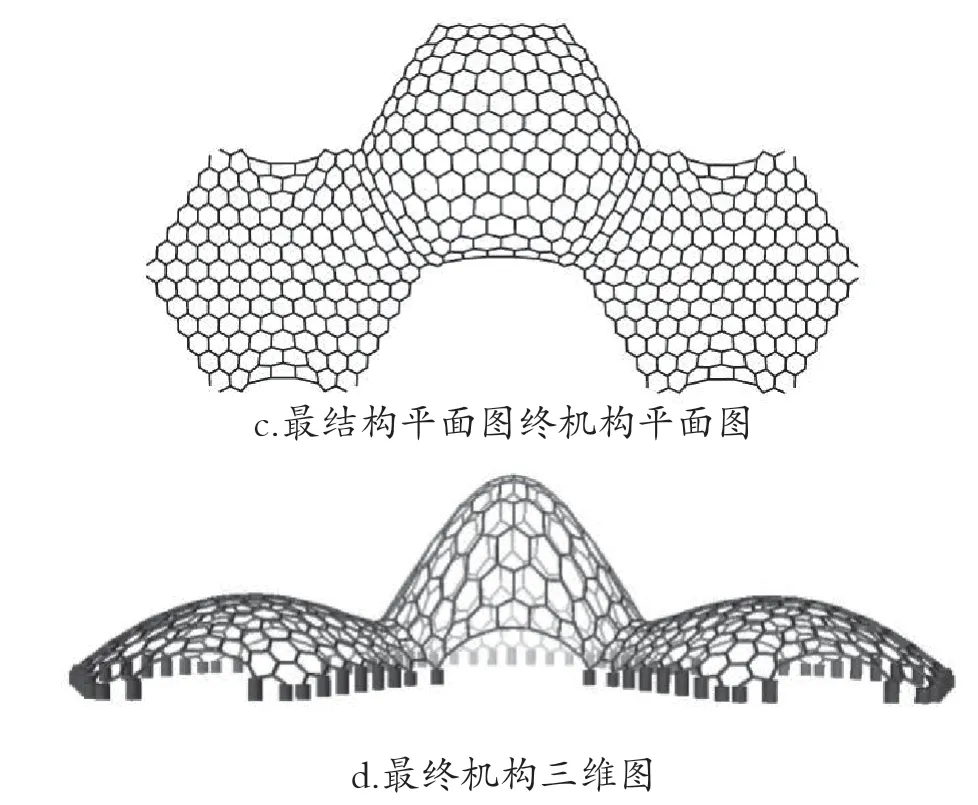
图4 自由曲面网格结构形态创构

三、结论

根据机构在荷载作用下改变其形状，达到机构势能最小状态时停留的机构性质，建立了适用于网壳结构的形态创建方法。该方法基于杆件长度不变的条件推导“移形方程”，并以势能减少最快的方向更新形状，最终得到自然平衡状态的机构形状。方法可以根据建筑空间要求控制构件长度，结构形态创构过程中初始模型预设的构件长度与最终结果中的构件长度可以保证一致，该特点对于建筑的设计与施工具有重要意义。在机构形状演变过程中，所对应的结构最大弯矩、平均弯矩、应变能均显著降低，且与轴力相比可忽略不计，表明结构趋于纯拉结构或纯压结构，该方法所得到的结构均为形效结构。