基于协方差估计的多因变量回归模型的多性状QTL定位研究
张 慧,叶景山,申佳瑜,刘慧铭,尹 宁,李立婷,温永仙
(1 福建农林大学a计算机与信息学院,b统计及应用研究所,福建 福州,350002; 2 漳州农业发展集团有限公司,福建 漳州,363000;3 厦门华厦学院,福建 厦门 361021)
数量性状基因座(quantitative trait loci,QTL)与连续变化的数量性状表型有密切关系,常用DNA分子标记技术对数量性状基因遗传位置进行标记,QTL定位研究是遗传学领域的一个重点。
早期的QTL定位方法是利用分子标记与QTL之间的连锁关系,定位出QTL在染色体上的位置,并估算出相应QTL效应值。但初期的单个性状QTL定位存在一些问题。随后,研究者提出了多性状联合定位分析方法。Jiang和Zeng[1]提出了一种多性状的复合区间定位方法(composite interval mapping,CIM),利用所考虑性状的相关结构进行定位,可以提高QTL检测的准确性。还有研究结果表明,同时检测多个性状比单独检测1个性状更有效[2-4]。
多性状QTL定位的实质是在多因变量回归模型的基础上进行变量选择。近年来,很多学者尝试对多性状QTL定位进行研究。Jansen 和Stam[5]提出了参数多变量回归模型,研究多个性状与分子标记之间的关系,并通过极大似然比检验来找出与性状相关的QTL位点。但这种方法计算量较大,为此,Lange和Whittaker[6]提出广义估计方程,该方程不需要对具体分布进行假设,大大缩短了计算时间。肖静等[7]和Xiao等[8]提出了多性状主基因联合分离分析方法(multivariate segregation analysis,MSA),通过对比单个性状和多个性状联合分析的模拟结果发现,多个性状联合分析效果较好,统计功效和效应估计值的准确度也较高。Banerjee等[9]在多性状分析中引入贝叶斯模型,并结合马尔科夫链蒙特卡洛(markov chain monte carlo,MCMC)算法进行模拟,建立相关表型和不相关表型两个模型。Xu等[10]利用贝叶斯模型分析多个性状与分子标记之间的关系,通过压缩系数方式来估计所有标记区间内的遗传效应。
关于多性状联合基因关联分析,O′Reilly等[11]用MultiPhen方法,以可解释的方式同时快速模拟了多种表型,提高了功效[11]。Bolormaa等[12]和Zhu等[13]用meta分析方法对多个性状进行了基因关联分析。Cheng等[14]用混合先验贝叶斯回归方法进行多性状回归分析发现,其效果优于单性状基因关联分析。Tong等[15]结合期望最大化算法(expectation maximization,EM),提出多性状特征多区间下估计参数的方法(multiple trait multiple-interval mapping-new,MTMIM-NEW)。Montesinos- López等[16]用基于奇异值分解(singular value decomposition,SVD)的四阶段分析方法进行多性状基因关联分析发现,其在参数估计和预测精度方面与使用贝叶斯多性状多环境模型(bayesian multiple-trait and multiple-environment model,BMTME)获得的结果类似。Yang等[17]提出了一个具有多性状的全关联的整合函数线性模型,利用惩罚函数解决了单核苷酸多态性(single nucleotide polymorphism,SNP)的高维性和多性状相关性问题。Lin等[18]提出一种基于混合线性模型的多性状联合基因关联分析方法,模拟结果表明,多性状全基因组关联研究(genome-wide association studies,GWAS)在检测多效性位点的影响方面较单个性状效果更好。Tran等[19]在绘制多数量性状位点的统计方法中考虑到X染色体,扩展了一种多QTL模型选择的惩罚似然方法。
此外,还有一些降维方法被应用于解决多性状基因关联分析问题,包括主成分分析[20-21]、典型相关分析[22]、偏最小二乘法[23]和贝叶斯Lasso方法[24]。本研究采用Rothman等[25]提出的基于协方差估计的多因变量回归(multivariate regression with covariance estimation,MRCE)模型,通过计算机模拟产生基因型数据和性状表型数据,利用MRCE模型进行参数估计,探究基因位点解释的方差比、表型相关系数、遗传率对模拟效果的影响,并将此模型应用于水稻群体标记数据中,完成基因定位,估计其参数,以期为多性状QTL定位研究提供参考。
1 研究模型的构建
1.1 模型建立
假设一个遗传群体包含n个个体,若不考虑群体结构等因素,对第i个个体,在遗传关联分析中假设有p遗传标记为xi1,xi2,…,xip(i=1,2,…,n),若有q个数量性状,线性遗传模型可以表示为:

1,2,…,q;k=1,2,…,p)。
式中:yij表示第i个个体第j个性状表型值。xik表示第i个个体在第k个基因标记位点的指示变量值,若A和a表示1对等位基因,当基因型是AA时,xij取1;当基因型是Aa时,xik取0;当基因型是aa时,xik取-1。β0j代表第j个数量性状的均值,βkj代表第k个基因标记位点对第j个数量性状所表现的遗传效应值。εij为随机误差,一般εij之间不是相互独立的,假定它们服从均值均为0,协方差矩阵为∑的多元正态分布。当q=1时,模型为经典的单因变量回归模型。将线性遗传模型写成矩阵形式,分别用X、Y、B、ε表示:
则有:
Y=XB+ε。
Rothman[25]提出了MRCE,B的稀疏估计量,该方法在负对数似然函数上加入了两个惩罚项,求解B的稀疏估计值,具体形式为:
式中:Ω=∑-1=[ωj′j],∑-1是协方差矩阵∑的逆矩阵,ωj′j是逆矩阵中的元素。λ1≥0,λ2≥0,二者均是调整参数,用k折交叉验证来选择参数λ1和λ2。
1.2 模型的假设检验
首先,原假设效应系数都为0,通过基于Pillai-Bartlett迹、Hotelling-Lawley迹和Wilks’s Lambda的近似F分布检验进行模型检验[26-30]。其次,用Lβ=0的方法对基因标记位点的遗传效应βij(i=1,2,…,p;j=1,2,…,q)进行检验[31],其中L是c×p+1阶的矩阵,用来识别检验假设的遗传效应。如对β1j的假设检验可以写:
对于假设可采用F检验进行,F检验的形式为:
2 研究模型的模拟与实际应用
2.1 模拟试验设计
2.1.1 SNPs生成 参照黄杨岳等[32]的SNPs数据仿真方法,生成纯合SNP模拟数据SNPs,包含500个个体和200个基因位点,其基因型为AA、aa。
2.1.2 数量性状表型值生成的多元仿真框架 (1)给定截距b的合适值。
(2)按照Porter和O’Reilly[33]的方法,给定v值,v是遗传变异所解释的表型方差遗传效应向量。例如,当v=(0,1,0.5)时,对应于SNP,表示解释了性状1的 0.1%表型方差,性状2的0.5%表型方差。
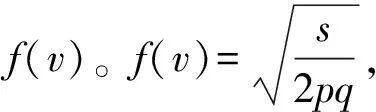
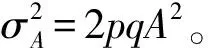
性状表型相关矩阵为R:
式中:ρij(i,j=1,2,…,q)表示第i个性状与第j个性状的表型相关系数。
则协方差∑为:
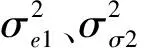
数量性状表型值y的计算公式为:
y=b+f(v)x+ε。
式中:x代表基因型指示变量,基因型为AA时取1,基因型为aa时取-1。
2.1.3QTL检验功效的计算 对于染色体上的某个基因位点需要对其进行参数估计及统计检验,若对于给定的显著性水平,该位点的遗传效应值达到显著,说明在该位点检测到QTL。若假设情况的计算机模拟共重复m次,染色体基因位点能检测到m0次,则该位点的QTL检测功效为m/m0。效应值是f(v),估计值是用MRCE方法估计的f(v)。
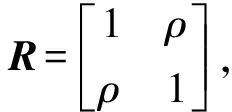
(1)模拟1。给定3组v值,v1=(0.5,0.5),v2=(0.5,0.1),v3=(0.5,0.0),计算相应的f(v):f(v1)=(0.1253,0.1253),f(v2)=(0.1253,0.0559),f(v3)=(0.1253,0.0000),进而得到相应性状表型值,利用MRCE模型进行参数估计,根据功效,比较v值对QTL定位模拟效果的影响。
(2)模拟2。设v=(0.5,0.5),相关系数从-0.9每次增加0.1直到0.9,分别产生相应的性状表型值,利用MRCE方法进行参数估计,探究相关系数对模拟效果的影响;同时设v=(0.5,0.1)、遗传率为(0.05,0.05)时,研究相关系数对QTL定位模拟效果的影响。
(3)模拟3。设v=(0.5,0.5),给定不同遗传率组合(0.05,0.05),(0.05,0.10),(0.05,0.15),(0.10,0.05),(0.10,0.10),(0.10,0.15),(0.15,0.05),(0.15,0.10),(0.15,0.15),对相应性状表型值进行功效模拟,分析遗传率对QTL定位模拟效果的影响。
2.2 实例数据收集
2.2.1实例1数据 实例1数据选自qtlnetwork软件,是一个水稻DH群体,包含12条水稻染色体中的3条染色体,共54个标记,每条染色体上标记数量不等,99个个体,2个环境(1998年和1999年)。由于水稻DH群体数据中存在缺失数据,需通过相邻平均值方法进行填补,再将1998年与1999年数据进行整合,最终得到的数据集为54个标记和198个样本量,提取ph6、ph8作为性状表型值,两性状的相关系数为0.9464。
2.2.2实例2数据 实例2数据是包含12条染色体的水稻永久F2群体试验数据[37-40],该群体由来自珍汕97×明恢63,含有210个株系的重组自交系(RIL)群体随机交配生成,共产生278个杂种株系,其遗传图谱共有1619个标记序号(Bin1~Bin1619),包含单株产量、分蘖数、穗粒数、粒质量4个性状,本研究仅对穗粒数和粒质量进行联合分析,剔除缺失数据后获得2组完整数据,其中1998年有246个,1999年有276个,为了简化考虑,本研究仅考虑其加性效应。
3 结果与分析
3.1 MRCE模型对QTL定位效果的模拟试验结果
3.1.1 模拟试验1 通过MRCE模型对不同v值情况下的QTL进行定位发现,任意给定一个固定的相关系数和遗传率时,不同v值对QTL定位的影响规律大致相同,所以本研究选择其中3个相关系数(0.1,0.5,0.9)且遗传率为(0.05,0.05)时进行分析,结果见表1。从表1可以看出,当相关系数分别为0.1,0.5,0.9,遗传率为(0.05,0.05)时,v值越大,功效越大;v为0时,功效为0或接近0。所以,如果遗传变异所解释的方差比大小合适,则利用MRCE模型进行QTL定位是可行的。
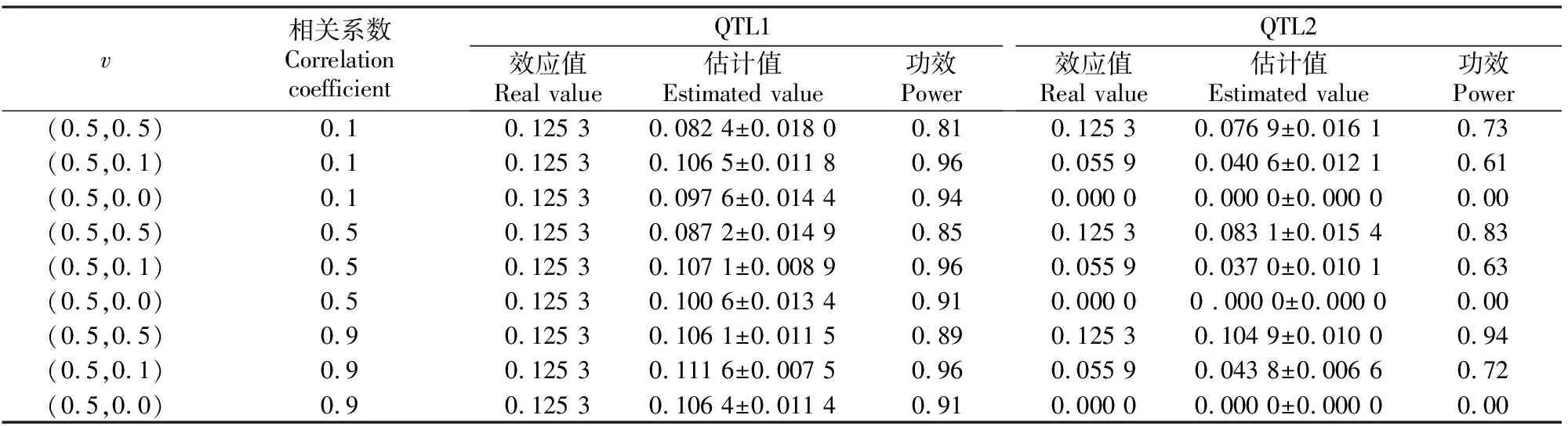
表1 不同v值情况下QTL定位的模拟结果Table 1 Simulation of QTL mapping with different v values
3.1.2 模拟试验2 图1表明,当v相同时,两端功效略高于中间部分,说明相关系数绝对值越大,其功效越高。

图1 v=(0.5,0.5)时不同相关系数对MRCE模型用于QTL定位模拟效果的影响Fig.1 Simulation of QTL mapping based on MRCE for different correlation coefficients and v=(0.5,0.5)
表2是当v=(0.5,0.1)、遗传率为(0.05,0.05)时相关系数对模拟效果的影响。从表2可以看出,相关系数绝对值越大,QTL1和QTL2估计值越接近效应值,功效也越高。可见MRCE模型可用于QTL定位。
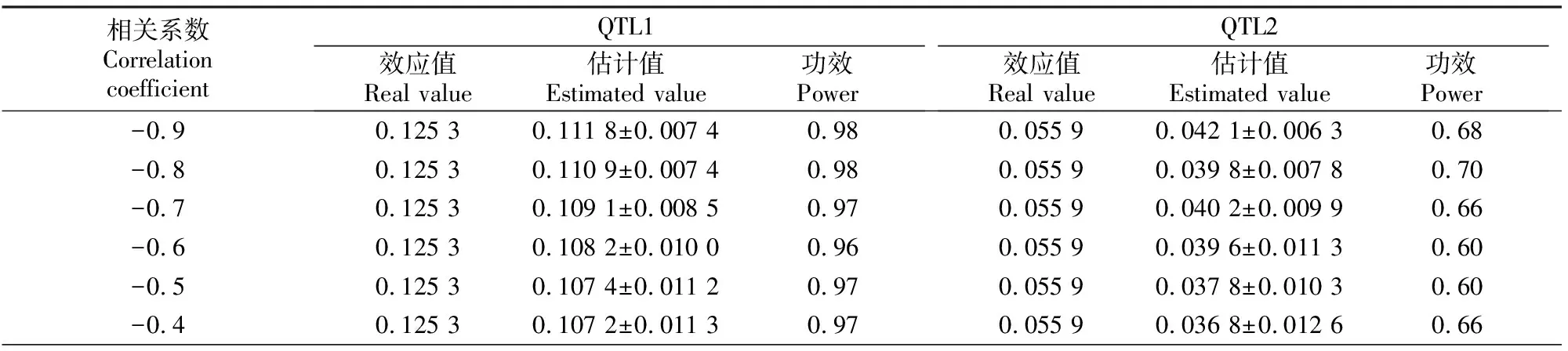
表2 v=(0.5,0.1)时不同相关系数情况下QTL定位的模拟结果Table 2 Simulation of QTL mapping with different correlation coefficients and v=(0.5,0.1)
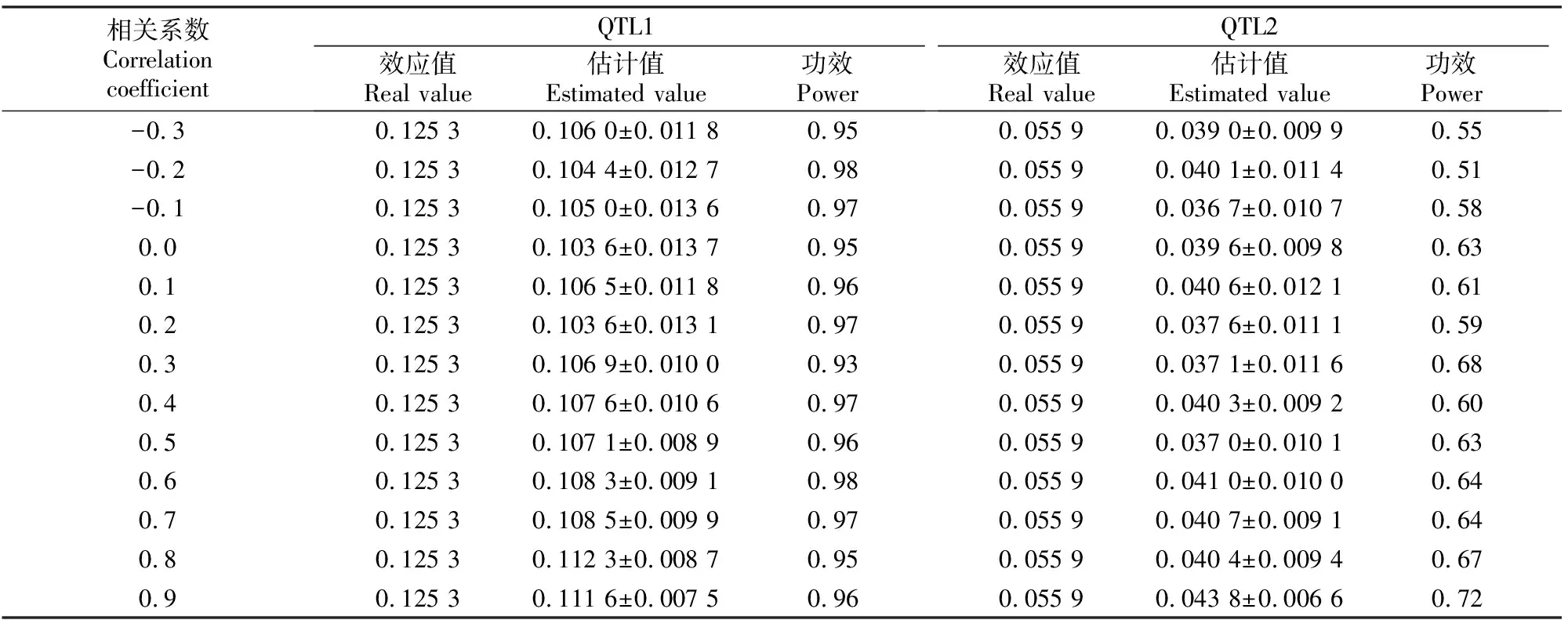
表2(续) ConutinuedTable 2
3.1.3 模拟试验3 分析v=(0.5,0.5)时遗传率对模拟结果的影响,结果见表3。

表3 v=(0.5,0.5)时不同遗传率下QTL定位的模拟结果Table 3 Simulation of QTL mapping for different heritability and v=(0.5,0.5)
从表3可以看出,遗传率越高,其效应估计值越接近真值,功效也越好,在其他不同遗传率假设下也有上述相似结果。综上可知,利用MRCE模型进行QTL定位分析是可行的,同时遗传变异所占方差比越大,相关系数绝对值越大,遗传率越大,则模拟效果越好。
3.2 MRCE模型对QTL定位效果的应用实例
3.2.1 应用实例1 表4和表5分别为用qtlnetwork软件和MRCE模型得出的水稻DH群体数据QTL定位结果,定位到的QTL均通过了显著性检验。

表4 基于qtlnetwork的水稻DH群体数据 QTL定位结果Table 4 QTL mapping for DH population of rice by qtlnetwork

表5 基于MRCE模型的水稻DH群体数据QTL定位结果Table 5 QTL mapping for DH population of rice based on MRCE
从表5可以看出,通过MRCE模型发现,8个标记MK6、MK15、MK16、MK18、MK31、MK32、MK52、MK54与ph6性状有关,6个标记MK15、MK16、MK18、MK31、MK52、MK54与ph8性状有关。
由表5还可以看出,与qtlnetwork软件定位的QTL结果对比,基于MRCE模型选出的标记中,有6个标记与真实结果一致,尤其是MK6这个标记仅与ph6有关;此外,还多定位到了3个标记,分别为MK18、MK32、MK52;且这些标记与qtlnetwork软件定位的QTL结果相邻。MK18与qtlnetwork软件定位的MK15-MK16相邻,MK32与MK30-MK31相邻,MK52与MK53-MK54相邻,多定位到的标记可能与邻近QTL效应的影响以及在qtlnetwork软件定位过程中的阈值设定有关,由此可知,基于MRCE模型的QTL定位与用qtlnetwork软件的定位结果基本相符,进一步说明MRCE模型应用于QTL定位是可行的。
3.2.2 应用实例2 由于MRCE模型不能用于样本量(n)小于遗传标记个数(p)的情况,所以本研究计算了遗传标记与性状表型值的边际相关系数,且边际相关系数越高,则该遗传标记与对应性状表型值的相关性越高,最终选取边际相关系数绝对值较大的200个标记数据进行初步降维,QTL定位结果见表6。表6表明,利用MRCE模型检测到1998年穗粒数在第3、第6和第7条染色体上各有1个QTL;粒质量在第1和第5条染色体上各有3个QTL,第3和第7条染色体上各有2个QTL。利用MRCE模型检测到1999年穗粒数在第3条染色体有1个QTL,第7条染色体有2个QTL,粒质量第1和第3条染色体各有1个QTL,第5和第7条染色体各有2个QTL。对比1998和1999年的定位结果可知,穗粒数都定位到Bin436,粒质量都定位到Bin65、Bin439、Bin699、Bin769和Bin1008,是因为1998年穗粒数与粒质量2个性状之间的相关系数(0.15)大于1999年(0.05),故1998年定位出更多QTL。
综合实例1和实例2的结果,说明MRCE模型不仅可以用于模拟QTL定位,而且在实际定位中也同样适用,结果较好。
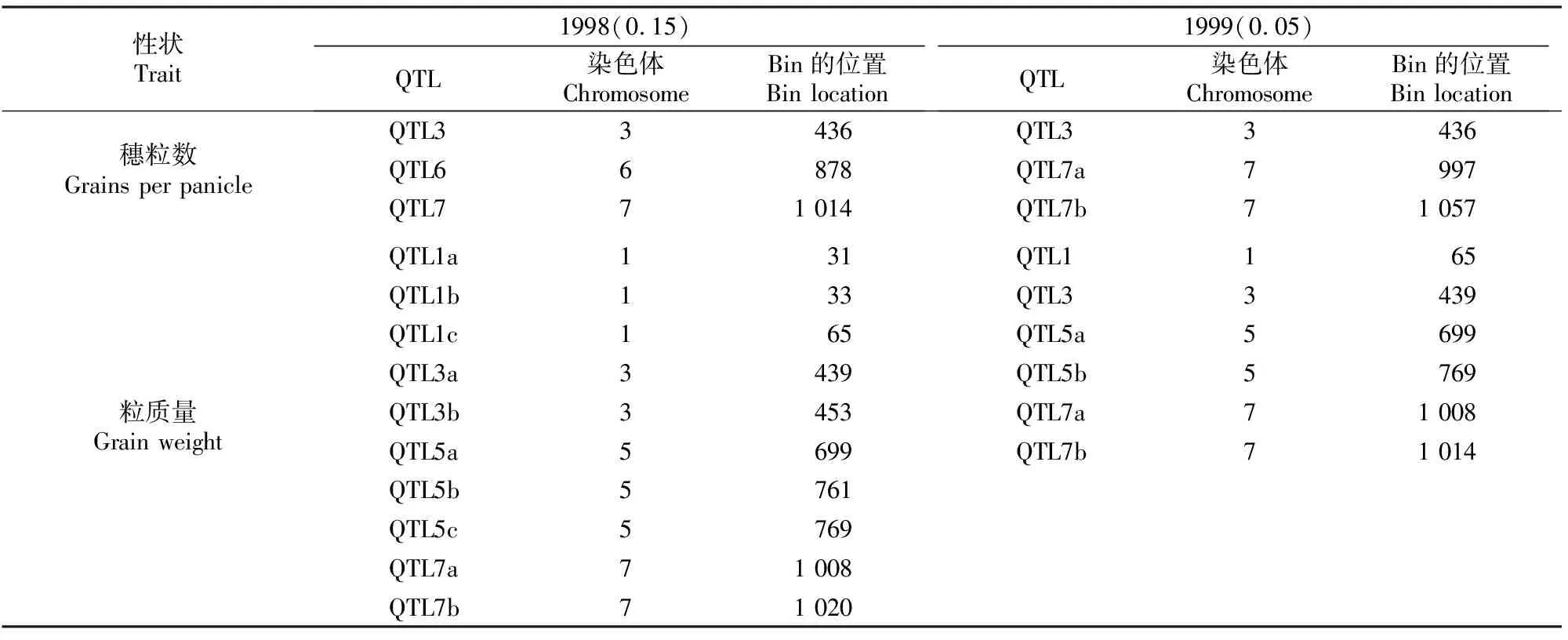
表6 基于MRCE模型的水稻永久F2群体穗粒数和粒质量的QTL定位结果Table 6 QTL mapping of grains per panicle and grain weight for immortalized F2 population of rice by MRCE
4 讨 论
采用不同的QTL定位方法和不同数据检测到的QTL数目和位置可能有差异,若能定位到更多的QTL,在一定程度上可以弥补用其他方法未找到的备选QTL,但是否是真实的QTL,需用生物检测方法进行验证。Yu等[39]用超高密度SNP图谱,检测出穗粒数性状在第1、第3和第7条染色体上各有1个QTL,粒质量在第1和第3条染色体上各有2个QTL,第5和第9条染色体上各有1个QTL。对比本研究结果可以发现,利用MRCE模型检测出的穗粒数、粒质量QTL更多;其中1998年的数据中多检测出穗粒数第6条染色体上的1个QTL,粒质量多检测出第7条染色体上的2个QTL,且与Yu等[39]检测到的QTL位置大致相近;但本研究利用MRCE模型检测时丢失了穗粒数第1条染色体上的1个QTL和粒质量性状第9条染色体上的1个QTL、第1条染色体Bin172位置附近的1个QTL。原因可能是只考虑了加性效应而没有考虑显性效应,或丢失QTL的LOD值都比较小,刚好超过给定的阈值[39]。
本研究仅验证了MRCE模型定位QTL的可行性和优势,即表型性状联合定位时相关系数越大,效果越好。且MRCE模型不适用样本量小于维度的情况,对此情况可利用降维手段,先将高维数据降为低维。对于水稻永久F2群体数据分析中定位到的QTL少的问题,可以增加显性效应进一步研究。

