基于改进LSTM的原烟仓储堆垛内部温度预测方法

陈斌，方海英，周继来，许仁杰，周鹏，杨文静，赵维晞，潘楠

（1.红云红河烟草（集团）有限责任公司物流中心，云南 昆明 650202；2.昆明理工大学民航与航空学院，云南 昆明 650500）

0 引言

目前，在原烟仓储管理中，片烟已成为原烟的主要贮存形式，存储片烟的堆垛内部温湿度环境直接影响其醇化效果，管理员根据温湿度数据可对片烟储存进行有效管理，一旦出现温度过高等问题管理员可以及时采取措施，以避免烟叶产生霉变等问题，减少损失。如果能有效预测出未来某短时间内的仓储温度，即可极大提高片烟精准监测水平，因此对片烟堆垛内部未来一段时间内的温度数据进行预测非常有必要。

关于仓储温度预测的方法，主要包括机器学习以及深度学习神经网络等技术。近些年来，人工神经网络取得了快速发展，包括深度神经网络（DNN）、长短期记忆网络（Long Short-Term Memory，LSTM）、卷积神经网络（Convolutional Neural Network，CNN）等。Shi X，等将降水临近预报描述为一个时空序列预测问题，通过利用LSTM方法有效预测了降水临近的数据。Gundu，等提出了一个基于LSTM的预测模型，通过对各种网络模型进行统计分析，得到了适合准确预测太阳能和温度的网络结构。也有不少学者将上述人工神经网络相结合，其中，倪铮，等提出了一种针对气象数据的CNN-LSTM神经网络，并利用其对雷暴的6h临近预报进行了实验，取得令人满意的预报效果。Tabrizi S E，等采用将CNN与LSTM相结合的DNN模型应用于路面表面温度预测，相较于其他单一的神经网络取得了较好的预测效果。此外也有学者将其他方法与神经网络相结合，其中，张亚伟，等提出了结合长短期记忆神经网络LSTM与梯度提升算法LightGBM的组合模型，该方法可以保留LSTM模型对单变量预测的周期性特点，结果表明，基于LSTMLightGBM的组合模型方法比单纯使用LSTM的方法更接近原始波形，具有更低的RMSE。黄伟建，等提出一种基于混合神经网络和注意力机制的预测模型（Att-CNN-LSTM），王晨阳，等提出一种基于遗传算法（GA）优化的卷积长短记忆神经网络混合模型（GACNN-LSTM），通过GA优化LSTM训练网络的超参数权重与偏置值，经过仿真结果表明该方法对光伏发电功率具有更好的预测性能。

基于上述分析可知，单一神经网络在预测上精度都不够高，预测结果不够准确，应该将多种神经网络结合在一起，用其他方法的优势取代其劣势，从而达到对数据的精确预测。因此，本文首先利用自组织映射（Self-Organizing Maps，SOM）将输入的温度数据进行聚类，随后将数据集分成训练集和测试集，对这些数据进行归一化处理，以提高训练速度和计算精度，由于LSTM可以解决循环神经网络（Recurrent Neural Network，RNN）中梯度消失和梯度爆炸、长期记忆能力不足的缺点，因此，本文提出了基于粒子群算法的混合长短记忆模型（PSO-SOM-LSTM），对数据进行预处理，基于粒子群算法优化SOM-LSTM的网络权重，随后带入神经网络进行数据预测，实现对未来仓储堆垛内的温湿度进行精准预测的目的。具体步骤为：首先对数据进行预处理，将数据归一化再采用SOM聚类分别构建各类数据集；其次构建LSTM神经网络结构，输入训练数据进行训练；随后，基于PSO算法优化SOMLSTM的网络权重，带入神经网络进行数据预测并与四种不同的预测方法进行对比，证明了PSO-SOMLSTM算法的优越性；最后通过均方根误差（RMSE）等指标来衡量实验结果。

1 数据预处理

本文实验数据由某大型卷烟生产企业原料仓储科露天堆垛在2021年4月25日-5月1日一周内的某一烟垛每间隔30min的温度监测数据拟合而成。传感器的最大布设上限为80个，传感器在室内中的摆放信息记录共分8段，由于篇幅问题，本文只选了第一段第一层的无线传感器摆放示意图，如图1所示。

图1 无线传感器摆放图（节选）

1.1 归一化

为了提高后面神经网络的训练速度和预测精度，将所有的温度数据进行归一化处理，公式如下：

其中：X是所用数据的平均值，是所用数据的最大值，是所用数据的最小值。归一化后的温度数据如图2所示。

图2 数据归一化

1.2 SOM聚类

对大量数据进行分析是一项繁重又复杂的工作，为简化该工作并且为神经网络提供不同类别的数据集，以提高预测精度，本文采用一种无监督学习SOM聚类方法。自组织映射神经网络（Self Organizing Maps，SOM）由芬兰神经网络专家Kohonen教授提出，一个神经网络接受外界输入模式时，将会分为不同的对应区域，各区域对输入模式具有不同的响应特征，而且这个过程是自动完成的。SOM能把繁杂的高维数据转换为简洁的几何关系，因此具有精简数据并达到高质量聚类分析结果的目的。

实现SOM聚类的步骤为；提取各条数据之间的差异性，将归一化后的数据划分为训练集和测试集，输入SOM神经网络，把相同聚类结果的数据归为一类，为下一步的LSTM神经网络提供不同类别的数据集，以提高预测精度。

2 算法模型

本文采用粒子群算法（PSO）优化SOM-LSTM混合神经网络算法模型，主要过程为：首先对数据进行预处理，将数据归一化再采用SOM聚类分别构建各类数据集；其次构建LSTM神经网络结构，输入训练数据进行训练；随后，基于PSO算法优化SOM-LSTM的网络权重，带入神经网络进行数据预测；最后输入温度训练数据进行训练，对未来附近时间段内的温度进行预测，通过均方根误差（RMSE）等指标来衡量实验结果。

2.1 SOM算法

竞争学习规则的学习步骤如下:

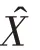
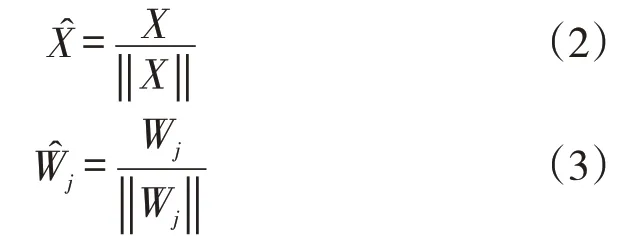
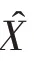
（3）网络输出与权调整。按WTA学习法则，获胜神经元输出为“1”，其余的神经元均为0，如下：

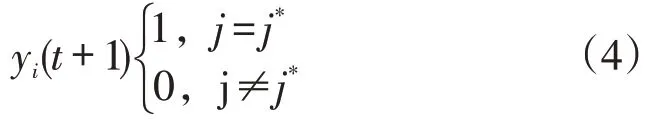
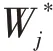
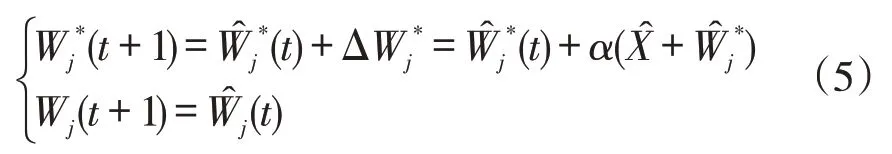
式（5）中，为学习效率，区间为[0,1]。

（4）重新归一化处理。权向量经过调整后得到新的向量，与之前的并不相同，因此要对该新向量重新归一化，直到学习率衰减到0。

2.2 LSTM算法

LSTM算法本质上是循环神经网络（RNN）的一种特殊模型，用来处理RNN训练过程中梯度消失和梯度爆炸的问题。其关键为细胞状态cell。如图3所示，LSTM拥有三个门来保护和控制细胞状态。三个门分别为输入门、遗忘门和输出门。

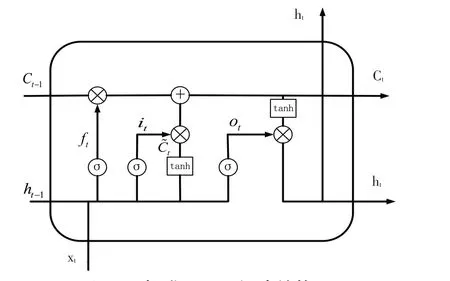
图3 标准LSTM细胞结构图

2.2.1 遗忘门。遗忘门会读取h和x，输出一个区间在[0,1]的数值，分配在每个细胞状态C中。1为保留，0为舍弃。

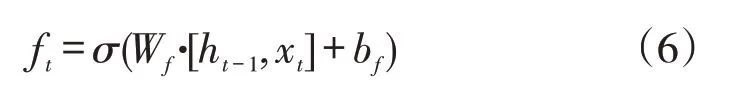
其中，h表示上一个细胞输出，x为当前细胞的输入。为一个向量，表示让对应信息通过的权重。

2.2.2 输入门。LSTM中第二步是决定让多少新的信息加入到cell状态中来。此过程包括两个步骤：

（1）层为“输入门层”，决定哪些信息将要更新；

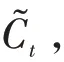
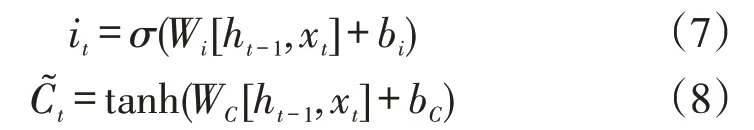
更新旧cell状态，C更新为C,新的候选值为：

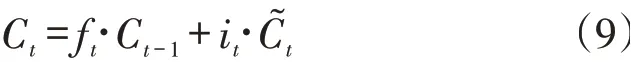
2.2.3 输出门。LSTM中的最后一步是确定输出什么值。此值基于cell状态，也是一个过滤后的值。运行式（11）确定细胞状态的哪个部分将会输出。通过tanh对cell状态进行处理。

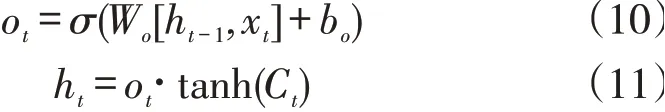
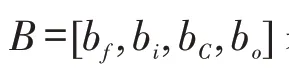
2.3 基于SOM-LSTM的传感器温度预测方法

构建SOM-LSTM神经网络结构，输入温度训练数据进行训练，同时对未来附近时间段的室内温度进行预测。总体算法流程如图4所示。

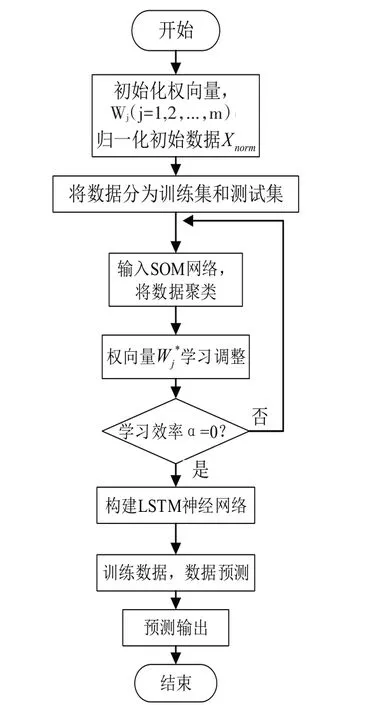
图4 SOM-LSTM总体算法流程图

2.4 粒子群算法（PSO）

粒子群算法是一种仿生群体智能算法，该算法将每个解都看作鸟群中的一个独立个体——“粒子”，每个粒子都有对应优化目标的适应值，因此，该算法的评价指标为适应值。由于PSO算法不用设置众多参数且简单易实现，因此，本文采用PSO算法优化LSTM，PSO算法的编码过程见表1。

表1 PSO算法伪代码

用PSO算法优化SOM-LSTM神经网络的具体流程如图5所示。

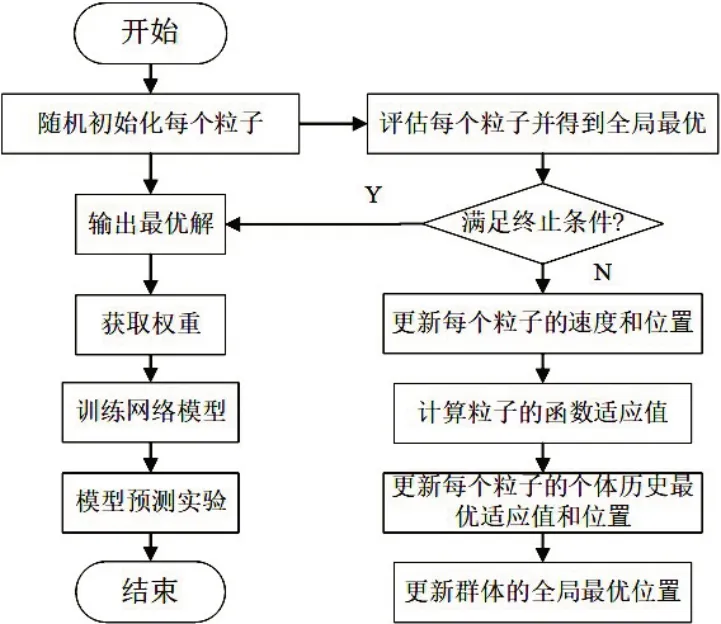
图5 粒子群算法优化流程图

3 实验分析与讨论

3.1 评价指标

本文采用均方误差（MSE）、均方根误差（RMSE）、相对误差和判定系数()等评价指标来衡量实验结果，以上评价指标为预测领域常用的评价指标。

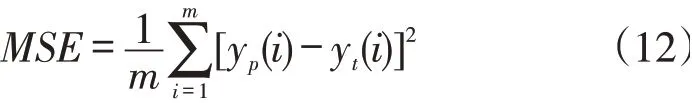
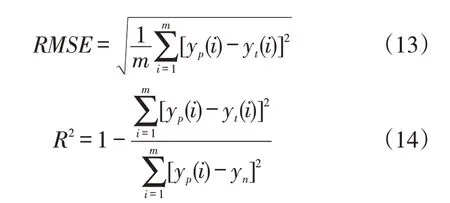
式中，y()为预测温度，y()为真实温度，y为真实温度的均值。通常，值越大，值越小，则预测的结果就越准确。

3.2 温度预测结果对比

为了验证PSO-SOM-LSTM方法的可行性，本文将该方法与LSTM、BP和SOM-LSTM神经网络算法预测效果进行了比较。采用MATLAB编程环境搭建并训练算法模型，本次实验选取136个真实数据为采样点，对不同的算法进行对比。其中，SOM-LSTM的梯度阈值设置为1，指定初始学习率0.002，在100轮训练后乘以因子0.2。图6为三种不同方法的温度预测效果。

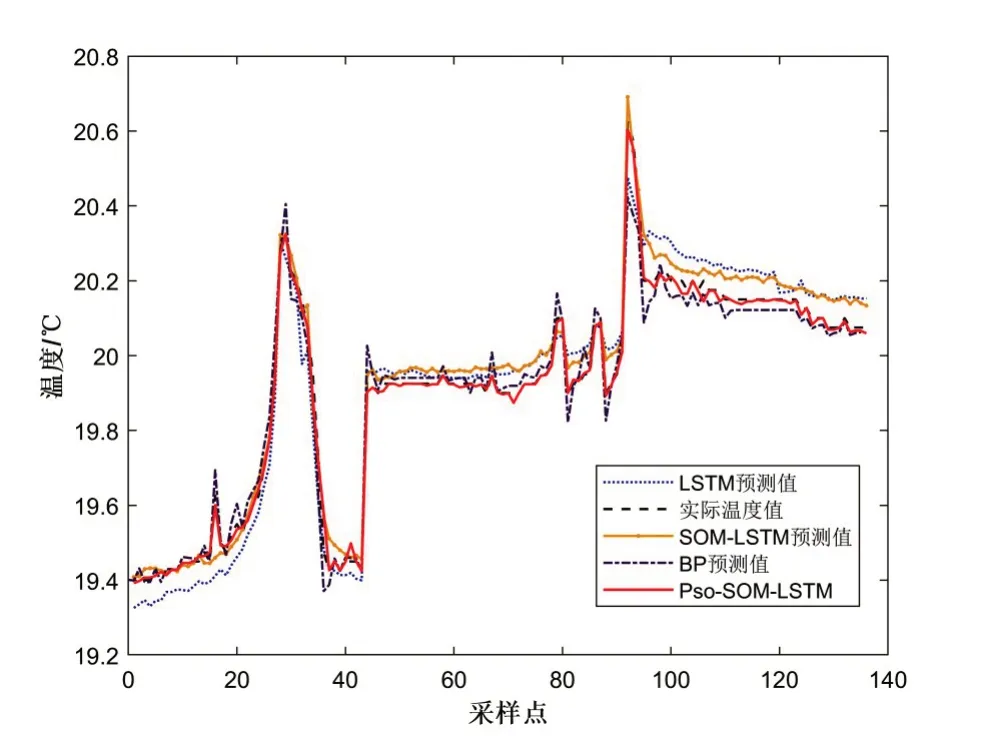
图6 不同算法下的温度预测值

由图6可以看出：BP神经网络在拐点处温度预测误差较大，预测结果具有不稳定性。LSTM和SOMLSTM都具有良好的稳定预测效果，但是预测值有偏差，相比于LSTM和SOM-LSTM，PSO-SOM-LSTM算法的预测值更贴近真实值，预测结果更为准确，因此采取PSO-SOM-LSTM算法对未来一段时间内的温度进行预测是最优的。

3.3 预测结果

由于采取PSO-SOM-LSTM算法对未来一段时间内的温度进行预测是最优的，为保障算法的适用性，随机选取仓库内某处的传感器，对同一个传感器未来时间段内的温度数据进行预测，选取285个数据作为训练数据，预测附近未来30个数据点，结果如图7所示。其中实线为训练值，虚线为真实值，星号线为预测出的温度数据：

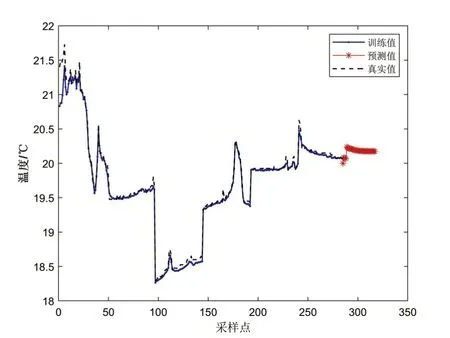
图7 基于PSO-SOM-LSTM的预测温度结果

4 误差性能指标

通过具体的相对误差指标分析预测的温度数据，图8为相对误差折线图，可以看出预测的相对误差主要集中在[-0.005,0.005]区间内，误差区间范围较小，在0.5%以内。

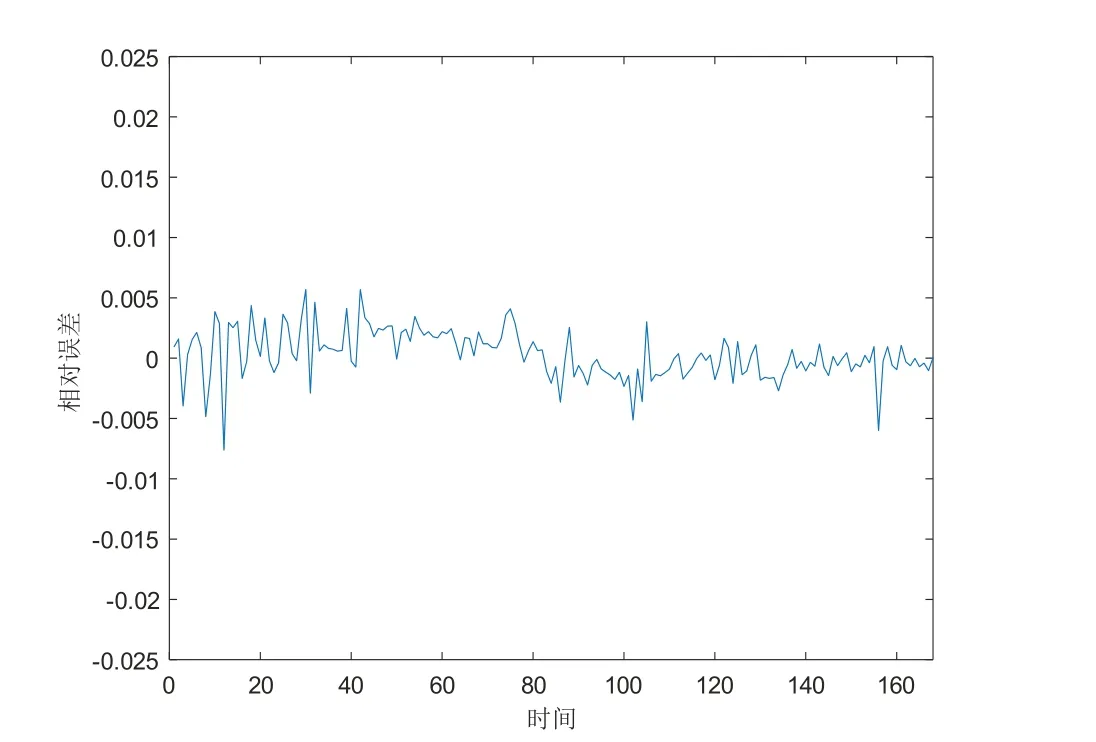
图8 基于PSO-SOM-LSTM预测温度的相对误差图

本文提出的算法与其他预测方法的预测误差对比见表2，由表2可以看出，BP预测效果最差，误差最大，PSO-SOM-LSTM的误差最小，预测结果最好。在RMS指标下，PSO-SOM-LSTM比SOM-LSTM减少了2.46%，比单一神经网络减少了8.94%，具有较优的预测效果。

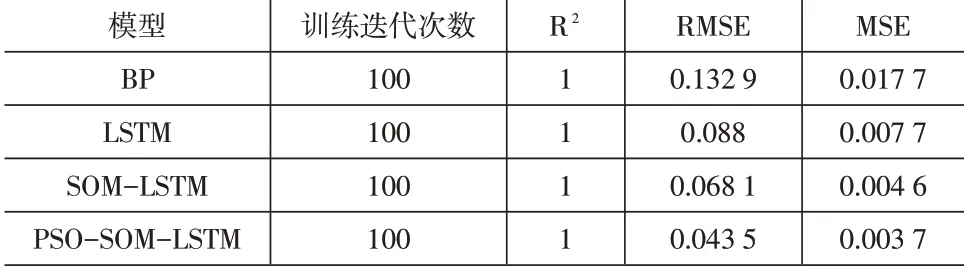
表2 不同算法的预测对比

5 结语

片烟仓储堆垛内部温湿度环境对片烟的醇化效果有很大的关联性，如果能有效预测出未来某短时间内的仓储温度，即可对片烟储存进行有效管理，能极大地提高片烟精准监测水平，如何对仓储空间内部的温湿度进行精准监控和预测，是片烟养护的一项重要工作。本文提出了基于粒子群算法的混合长短记忆模型（PSO-SOM-LSTM），首先对数据进行预处理，将数据归一化再采用SOM聚类分别构建各类数据集；其次构建LSTM神经网络结构，输入训练数据进行训练；随后，基于PSO算法优化SOM-LSTM的网络权重，带入神经网络进行数据预测，并与四种不同的预测方法进行对比，证明了PSO-SOM-LSTM算法的优越性；最后通过均方根误差（RMSE）等指标来衡量实验结果，计算出均方根误差为0.043 5左右。实验结果证明，通过PSO-SOM-LSTM模型算法优于本文所提到的其他算法，在实际仓储中能有效实现对未来某时间段内的温湿度进行精准预测的目的。