含高比例新能源的新型配电系统韧性资源调度

王婷婷，王 玥，于红丽，汤 奕，谷卫星，卢俞帆，韩建沛

（1.北京电力经济技术研究院有限公司，北京 100055；2.华北电力大学，北京 102206）

0 引言

配电网作为大电网与用户连接的“最后一公里”，其故障对社会生产生活将造成直接影响。近年来，飓风、地震、洪涝、海啸和冰灾等极端自然灾害的发生率急剧增长，对配电网造成较大的冲击。为缩小因自然灾害造成的停电范围，降低停电损失，亟须提高配电网应对极端自然灾害的能力，建设具备强抵御力、强恢复力的韧性配电网。另外，随着新型电力系统建设的进行，新能源装机容量占比不断提升。在该背景下，通过控制新能源主体的运行状态，提升系统韧性已是当前所面对的一大挑战。一方面，分布式电源与应急人员、应急电源车、应急物资等社会性资源，对提升配电系统韧性具有积极作用；另一方面，新能源的高比例接入和多种资源的复杂耦合关系增大了发生扰动或极端事件后的系统应急调度难度。

现有研究从提升配电网韧性的角度，分别应用了包含抢修人员、物资、移动电源在内的灾后应急资源和包含风电、光伏、小型燃气轮机等分布式电源来提升配网韧性。专家学者针对科学调派应急资源以提升配网韧性的问题进行了许多研究。文献[1]根据抢修人员到故障设备的位置对修复任务进行集群处理，以确保大型配电系统故障资源优化调度的高效进行。文献[2]考虑了不同类型故障的修复过程，将抢修人员工作分为修复故障和清除障碍物两类，并对抢修物资的物流约束进行建模。文献[3]同时考虑了抢修人员的调派策略与配电网重构技术，两种措施共同确保了配电网故障的快速恢复。文献[4]～[7]通过在灾后配网中接入移动电源来使失电负荷恢复供电。此外，分布式光伏等新能源的高比例接入，可能使配电系统以孤岛形式运行。在该背景下，许多专家学者针对新能源接入下孤岛运行这一韧性提升技术展开了研究。文献[8]将配电网灾后孤岛形成抽象为最大覆盖问题，并针对该问题进行求解。文献[9]针对灾后孤岛划分问题构建了分布式电源、柔性负荷和储能的多时间段故障动态恢复模型。虽然目前已有较多针对灾后应急资源调派、新能源接入形成孤岛以提升配网韧性的研究，但仍亟待同时考虑上述两种资源的耦合协同作用研究，在新型配电系统的背景下实现多种韧性资源的优化调度。

从韧性提升目标的角度，现有研究主要集中于以最小化停电时间和最小化甩负荷量为目标。文献[1]，[2]，[8]均以最小化停电时间为目标函数制定韧性提升策略；文献[3]～[6]以最小化甩负荷量为目标函数；也有一些文献以故障恢复成本、恢复 后 系 统 可 靠 性 为 目 标 来 指 导 故 障 恢 复[7]，[9]，[10]。现有研究大多注重于优化单一系统韧性指标，鲜有以综合多种系统韧性指标为目标进行研究。因此，以多重韧性指标为优化对象，研究多资源协同的新型配电系统韧性资源调度方法的意义重大。

为实现上述目标，本文提出了含高比例新能源的新型配电系统韧性资源调度方法。首先通过分析新型配电系统韧性的基本概念，研究了新型配电系统中分布式电源等多种韧性资源，提出了考虑多资源协同的韧性资源调度框架；再通过新型配电系统的韧性提升措施分析，建立了考虑鲁棒性与快速性的配电系统韧性量化指标。本文进一步考虑配电网、交通网以及各类韧性资源的运行约束，构建了含高比例新能源的新型配电系统韧性资源多目标调度模型，并提出了针对该多目标模型的转化与求解方法。

1 多资源协同的韧性调度框架

1.1 配电系统韧性的基本概念

从广义上来说，配电网韧性用于衡量配电网在应对由小概率极端灾害造成的故障时，是否能够通过改变自身状态以减少故障过程系统损失，并在故障结束后尽快恢复到原有正常状态的能力[11]。具体而言，配电网韧性特指其是否可以采取主动措施保证灾害中的关键负荷供电，并迅速恢复断电负荷的能力。配电网韧性包含了配电网对蓄意攻击或者自然灾害等事故的承受和恢复水平。韧性配电网应具备如下3种能力：①故障灾害发生前应具有做出相应准备和防御的能力；②故障灾害发生过程中应具有抵御、吸收和适应的能力；③故障灾害发生后应具有快速恢复到正常状态的能力[12]。为使韧性配电网具备上述3种能力，应在事前加强应急资源的布点，采用科学有效的故障诊断方法，在事后利用多种资源实现配电网故 障 快 速 恢 复[4]，[13]～[15]。

1.2 新型配电系统运行中的韧性资源

与传统配电系统相比，新型配电系统的分布式电源占比大大提升，配电系统能以孤岛形式运行，提升配电系统的韧性。除了传统的人、车、物等灾后应急保障资源之外，新型配电系统中的韧性提升资源还包括分布式光伏发电和风力发电。

1.2.1分布式光伏发电

分布式光伏发电有并网型和离网型两种运行模式。光伏电站多以自发自用、多余电量上网的模式运行，且在配电系统平衡中起着调节作用，具有长期边际成本高，短期边际成本低的特点。

光伏阵列的输出表达式为

式中：ηPV为转换效率；SPV为光伏阵列的面积；GPV为太阳辐射强度。

光伏出力受太阳辐射的影响较大，具有很强的随机波动特征，正午时分光照强度大，光伏出力多。典型日光伏负荷近似为正态分布。

1.2.2风力发电

风力发电出力受风速影响较大，其关系如式（2）所 示。

式 中：PR为 风 机 的 额 定 功 率；νr，νin，νout分 别 为 风机的额定风速、切入风速和切出风速。

风速近似服从威布尔分布，可由式（3）～（5）计算：

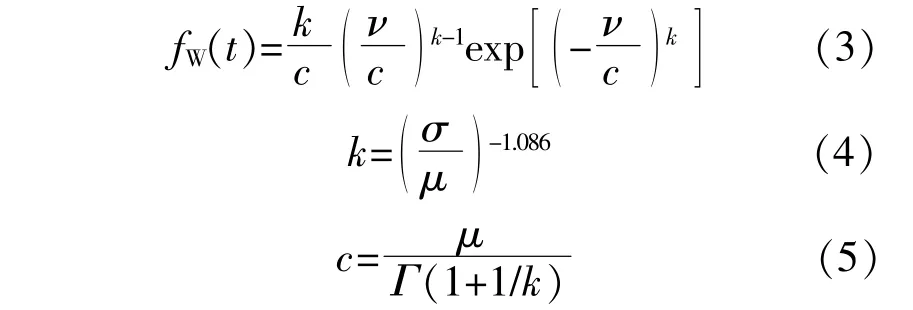
式中：ν为当地风速；k为形状系数；c为尺度系数；μ，σ分别为风速的均值和标准差。

此外，储能装置、电动汽车、温控负荷等需求侧灵活性资源也可作为配电系统的韧性提升资源。为了方便问题分析，本研究重点关注分布式新能源发电对提升系统韧性的作用。

1.3 多资源协同的韧性调度框架

新型配电网的多资源协同韧性调度框架如图1所示。在交通网中考虑应急抢修资源调派措施；在配电网中考虑新能源的接入以形成事后孤岛；通过交通网和配电网中韧性资源联动调配来实现配电网故障的快速恢复。在交通网中针对特定故障优化抢修路线、抢修人数和物资数来保证故障维修时间最短。在配电网中通过接入分布式光伏、风力发电装置等来实现对停电区域的快速电力供应。通过对两种网络中不同资源的协同布置，进一步提升新型配电网的韧性。本研究基于如下两方面假定：①系统中无功备用充足，无功处于平衡状态；②系统节点电压满足运行约束[16]，[17]。基于该假定，本文采用直流潮流对配电线路容量约束进行建 模[18]。

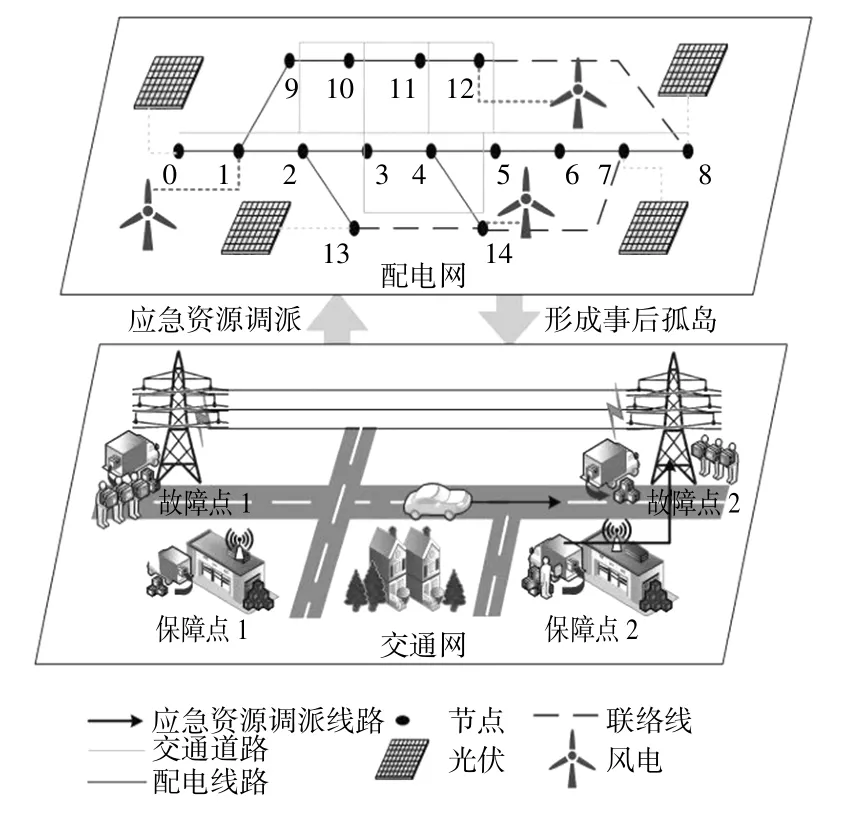
图1 多资源协同的韧性调度框架Fig.1 Resilience scheduling framework with multiresource coordination

2 新型配电系统韧性提升措施分析与量化

2.1 新型配电系统韧性提升措施分析

配电系统在遭受自然灾害、人为攻击等极端事件后，因元件故障等原因导致系统性能下降；故障消除后，系统逐渐恢复到原有的正常状态。图2为配电系统在整个极端事件影响过程中的功能曲线示意图[19]。系统状态分为正常状态、抵御事故、降额运行和故障恢复。假定t1时刻发生极端事件，系统元件于t1～t2时段遭到物理破坏，系统功能开始 下 降；t2～t3时 段 系 统 维 持 降 额 运 行 状 态；t3～t4时段为故障恢复状态。由于应急措施的实施，系统功能逐渐恢复。

图2 极端事件下配电系统功能曲线Fig.2 Function curve of system under extreme events

图2显示，提升系统韧性的原理可分为3个维度：一是减小极端事件的影响，采取加强线路元件强度、架空线路电缆化等措施，通过缩小由极端事件导致的故障规模来提升配电系统韧性；二是减少故障恢复过程中的负荷损失，通过接入分布式新能源发电或进行网络重构，为重要负荷提供功率支撑；三是减少故障恢复过程的持续时间，通过合理调配应急抢修人员、应急车辆、应急物资等来提高故障的修复速度，进而提高系统韧性。本文的研究范围为t3～t4的故障恢复阶段，重点关注故障发生后分布式新能源发电以及应急抢修人员、抢修车和电源车等应急车辆、应急物资等社会性资源对于提升系统韧性的作用。在该阶段主要采取两项举措：①通过优化分布式新能源发电的出力，减少系统失负荷量；②通过对应急抢修人员、应急车辆、应急物资的优化调度，使负荷停电时间、失负荷量和调配成本最小化。

2.2 新型配电系统韧性量化指标

为有效量化新型配电系统在极端事件下的韧性，参考文献[20]从鲁棒性、快速性和冗余性3个维度定义的海岛综合能源系统韧性指标；结合本文研究重点，不增加系统备用元件，设置鲁棒性指标和快速性指标来量化新型配电系统韧性。

2.2.1鲁棒性指标

鲁棒性反映了配电系统有效抵御极端自然灾害的影响，使之维持较高负荷水平的供能能力。通常以故障对系统性能函数减少的百分比来表征鲁棒性指标，鲁棒性指标越小说明鲁棒性越好[21]。本文采用配电系统的失负荷比例来表征系统性能函数损失的程度，系统的失负荷比例越高，表征系统维持负荷持续供电的能力越差，从而反映了系统的鲁棒性越低[20]，[22]。失负荷比例用下式计算：

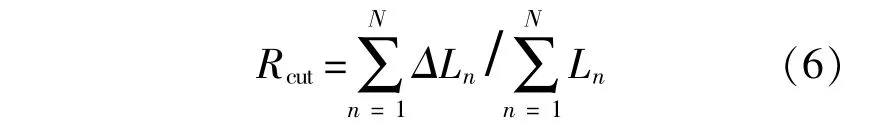
式中：N为配电网络节点个数；ΔLn为配电网络节点n的失负荷量；Ln为极端事件发生前节点n的负荷量。

失负荷比例越小，配电系统的韧性水平越高。

2.2.2快速性指标

快速性指标表征配电系统由降额运行状态恢复到正常状态的快慢程度。与运输时间和维修时间相比，分布式新能源发电功率调整时间和应急电源车接入电网时间可忽略不计，即快速性指标通过配电系统负荷停电时间表达：

3 韧性资源优化调度模型

3.1 韧性资源多目标优化调度模型

当极端事件导致配电系统发生单点故障，系统中存在多个应急保障点，在进行应急资源优化调度时，须要协同考虑分布式新能源发电、应急人员、应急车辆、应急物资等多种韧性资源，使配电系统鲁棒性、快速性和调配成本达到最优。本文构建的配电系统韧性资源多目标优化调度模型如下。

3.1.1优化目标

（1）最小化失负荷比例

配电系统失负荷比例如式（6）所示。其中，配电网络节点n的失负荷量 ΔLn可通过下式计算：

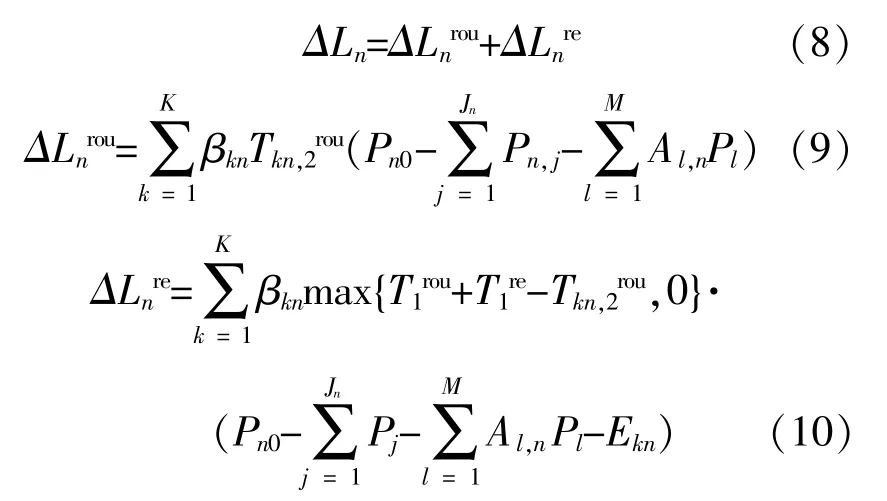
（2）最小化停电时间

如式（7）所示，故障后系统停电时间由抢修资源的运输时间与维修时间两部分组成。运输时间是抢修人员、抢修车辆、应急物资从保障点到达故障点的时间，由所选路程远近决定。维修时间是抢修人员修复故障所需的时间，与抢修人员的业务水平以及所配备的应急物资有关。假定不同保障点抢修人员的维修时间不同，可按下式进行计算：

式中：αk为0-1变量，若保障点k的抢修资源送往故障点，则取值为1，反之则为0；保障点k与故障点的地理距离；νavg为抢修车辆的平均行驶速度；保障点k抢修人员的平均维修时间，本文取为给定的常数。

（3）最小化调配成本

应急调度过程中的成本主要包括分布式电源的发电成本CDG、抢修车的行驶成本C1、电源车行驶和发电成本C2。

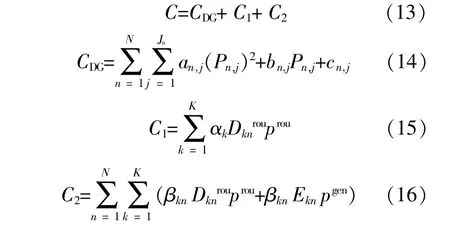
式 中：anj，bnj，cnj分 别 为 配 电 网 节 点n分 布 式 电 源j的成本系数，该系数取决于发电过程中的燃料消耗状况，如果为分布式新能源则不计其发电成本；prou为应急车辆的单位距离成本系数；为应急电源车由保障点k到配电网节点n的行驶距离；pgen为电源车的单位发电成本。

3.1.2约束条件

（1）配电网约束

式（17）为 节 点 功 率 平 衡 约 束；式（18）为 分 布式新能源发电出力约束；式（19）为线路潮流约束。

（2）应急保障约束

式（20）表示每个配电网节点n的电源车只由一个保障点来提供。式（21）表示故障点的抢修资源只由一个保障点来提供。式（22）表示应急电源车k的出力不能超过其上限Ekmax。式（23）表示每个应急保障点k所调派的电源车数量必须小于保障点所配备的车辆总数Xk。

3.1.3多目标优化模型

综合以上所述的韧性资源多目标优化调度模型表述如下：

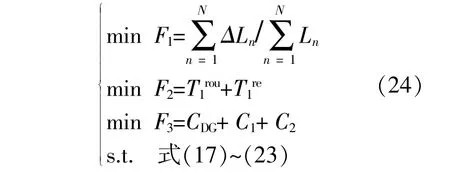
3.2 多目标模型转化与求解

对于式（24）所示多目标优化问题，由于优化目标F2仅与抢修资源的调配决策有关，且F2的取值越小，ΔLn和C1的取值也越小，故目标函数F2与F1，F3并 不 冲 突。因 此，式（24）所 示 多 目 标 优化问题可实现解耦求解，即先优化目标函数F2，基于所得结果再优化目标函数F1，F3。由于目标函数F1，F3存在冲突，为了方便问题求解，本文采用加权求和法对于目标函数F1，F3构成的多目标优化模型进行求解。通过引入权重系数ω，则由目标函数F1，F3构成的多目标优化模型可转化为如下单目标优化问题。

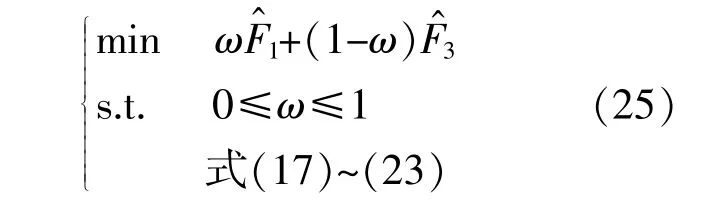
不断变化 ω的取值，可通过求解式（25）所述单目标优化问题得到pareto解集。采用模糊隶属度来表征对每个pareto解的满意度：

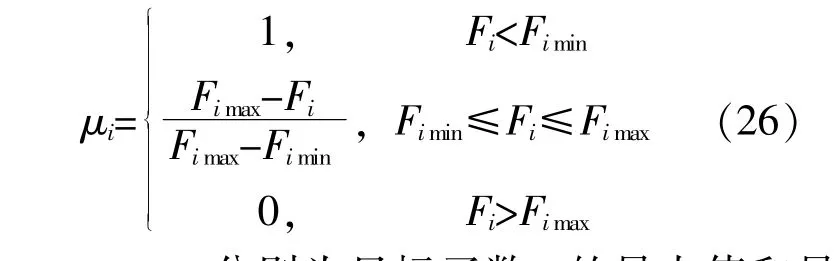
式中：Fimax，Fimin分别为目标函数i的最大值和最小值。

本文中i=1，3。当 μi=1时表示对第i个目标完全满意；当 μi=0时表示对第i个目标完全不满意。对于每个pareto解，通过计算标准化满意 度 μ=（μ1+μ3）/2来 表 征 决 策 者 对 该 解 的 满 意 程度。遍历整个pareto解集，标准化满意度最大的解即为最优折衷解。

4 算例分析

4.1 算例参数

基于改进的IEEE-33节点配电系统进行仿真分析，配电网络与交通网络拓扑如图3所示。交通网络配备3个应急保障点，其中每个保障点包括一组应急抢修人员、抢修车辆、应急物资和3台100kW电源车。配电网络节点12，17，26中接入分布式新能源。在仿真分析中，给定应急车辆在交通网络上的平均行驶速度为1.2km/min，3个保障点应急人员对故障的平均修复时间分别为25，10，18min。

图3 改进的IEEE33节点测试系统拓扑Fig.3 The topology of improved IEEE-33node test system

假定极端事件导致配电网线路8-9发生故障，此时图3中区域I所示配电网络呈孤岛运行模式。本算例重点分析分布式新能源发电以及应急人员、应急车辆、应急物资等韧性资源协同优化对于提升配电系统韧性的作用。

4.2 优化结果

4.2.1韧性资源多目标优化结果

对于式（24）所述的多目标优化问题，可实现优化目标F2与F1，F3的解耦目标。通过求解以F2为优化目标的停电时间最小化模型，得到最短的故障恢复时间为38.83min。应急抢修人员、抢修车辆及抢修物资的调配路线如图4所示，即由保障点3派出抢修人员、车辆、物资到故障点。其中物资运输时间为20.83min，故障修复时间为18min。

图4 抢修人员、车辆、物资的优化结果Fig.4 Optimized results of emergency crews，trucks and materials

对于式（25）所示的单目标优化问题，给定权重 系 数ω=0，0.01，0.02，…，1.00，共 计101个 权 重系数取值，分别求解式（25）所示优化模型，得到pareto解集如图5所示。由图5可见，随着系统失负荷比例的不断降低，应急资源的调配成本呈不断增加趋势。因此，对于决策者而言，配电系统中韧性资源优化调度是系统失负荷比例与应急调配成本折中的过程。

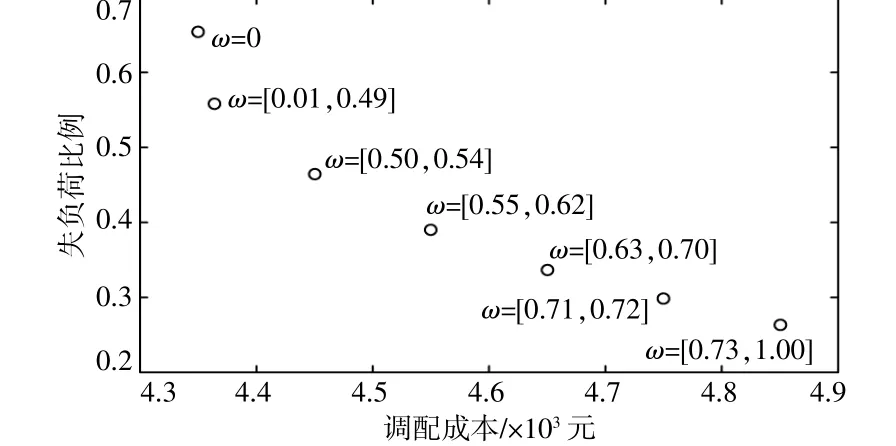
图5 Pareto最优解集分布Fig.5 Distribution of Pareto optimal solution sets

通过式（26）计算每个pareto解的模糊隶属度值，选取取值最高的pareto解作为最优解。本文中得到当 ω在[0.55，0.62]内取值所对应的pareto解模糊隶属度取值最高，此时的优化调度结果如图6所示。由于分布式新能源发电不计调度成本，故此场景下配电网节点12，17的分布式新能源发电满发（即分别为80kW和120kW），充分发挥了缓解负荷削减的作用。保障点1派出1台电源车沿路线l1到达需求点D1，向需求点供电功率为26 kW。保障点3派出1台电源车沿路线l2到达需求点D2，向需求点供电功率为50kW。

图6 电源车优化调度结果Fig.6 Optimal scheduling results of power supply vehicles

4.2.2多韧性资源协同优化效果分析

为了进一步分析不同韧性资源对于降低配电系统负荷削减的效果，设置如下3种方案进行对比分析。方案1是本文所提出的考虑分布式新能源发电和电源车的韧性资源调度方法；方案2是在方案1的基础上不考虑分布式新能源发电；方案3是在方案1的基础上不考虑电源车。不同方案的优化结果如表1所示。

表1 不同方案优化结果对比Table1Comparison of optimization results of different schemes

对比方案1和方案2可以得出，分布式新能源发电对于提升配电系统韧性具有显著作用（系统失负荷比例降低了42%）。由于不计分布式新能源发电成本，故有利于降低系统的调配成本。对比方案1和方案3可以看出，与不考虑电源车接入相比，在发生故障后，由于分布式新能源发电出力有限（优化结果为分布式新能源发电满发），通过应急电源车的优化调度，可以为负荷提供电力支撑；系统的鲁棒性指标比不考虑电源车接入提高了28%。方案对比结果验证了所提韧性资源协同调度方法的有效性。

5 结论

本文围绕极端事件下新型配电系统的韧性提升问题，重点关注故障恢复过程中韧性资源的优化调度。通过分析新型配电系统中存在的韧性资源，以分布式新能源发电、应急人员、应急车辆、应急物资等为对象，提出了多资源协同的新型配电系统韧性调度框架，建立了考虑鲁棒性与快速性的韧性量化指标，提出了韧性资源多目标优化模型与求解方法。

通过仿真分析显示：①由于分布式新能源不计发电成本，可在故障发生后为配电系统提供功率支持，支撑配电系统孤岛运行，有效降低系统的失负荷比例，因此对于提升配电系统韧性具有积极作用；②应急电源车具有灵活性接入的特点，可直接接入到需求点为系统提供支撑。