违约风险下混合养老金的最优投资策略

王 奕，王传玉，刘 帅

(安徽工程大学 数理与金融学院，安徽 芜湖 241000)

2008年金融危机过后，许多国家的养老金发展出现了资产价值大幅缩水、现期缴费不足、养老金福利大幅减少等问题，加剧了人们对潜在灾难性养老金违约风险导致养老金福利大幅减少的担忧，这种担忧来源于全球金融环境的不确定性和全球人口趋势带来的压力。预期寿命延长和出生率下降的现况使得公共养老金制度面临的财政压力越来越大。大多数发达国家的支持比例(Support Ratio，在职人员/养老金领取人员)也在不断下降，有关养老金的财政赤字预计将在可预见的未来继续存在，养老金计划将不可避免地受到资金赤字的负面影响，因此养老金福利不得不随之减少。传统的养老金计划正在经受着现实的考验,越来越难以满足养老金市场的需求，兼具确定给付(Defined-benefit,DB)和确定缴费(Defined-contribution,DC)型特点的混合型计划开始大量出现。混合型养老金计划的一个主要目标是在可持续、稳定和负担得起的基础上提供更好的退休保障，将养老金风险在雇主和雇员之间、不同年龄组之间进行不同程度的分摊，使得养老金计划显得更加公平。计划的管理者不仅为计划的参与者建立个人账户进行独立投资，还为计划的参与者制定了一个相对固定的养老金收益标准。近些年来，保险公司正在积极参与交易具有违约风险的高收益债券，由于养老基金的投资期限较长，债券违约事件的发生会为养老金计划的连续性带来影响。因此，考虑保险公司在可违约债券上的投资选择是很有必要的。

国内外学者对混合型的养老金计划进行了一定的研究，Kevin等[1]的一份研究报告介绍了传统的DB和DC计划的风险分担方式和混合养老金计划的全面知识，以及全球混合计划的发展情况，提出了发展混合型养老金计划的重要意义。Turner等[2]评估了国际上不同国家的混合计划的种类，并以四种不同的混合方案为案例进行了深入的研究：荷兰的混合型DB计划，瑞典的非金融DC计划(Nonfinancial DC Plan)，美国、加拿大和日本的现金平衡计划(Cash Balance Plans)，以及德国的李斯特计划(Riester Plans)，此外还构建了混合方案进一步分类的风险指标体系。陈凯等[3]分析了两种典型的混合型养老金——传统DB模式与DC模式混合型养老金和保证固定收益率的混合型养老金，将养老金的固定收益保证视为欧式期权，利用Black-Scholes模型进行期权定价，最后发现在实务中保证固定收益率的混合型养老金更具有优势。

基于养老金计划的最优资产配置策略研究，大部分学者都是在无风险资产和风险资产构成的财富组合下，研究年金的财富投资问题。一类文献主要研究DB型养老金的最优缴费问题和最优投资问题，而对于DC型养老金，因为缴费率提前确定，未来的养老金支付水平将完全取决于参保人的缴费水平和养老基金投资运营的投资收益，所以对投资和风险问题的研究居多。Boulier等[4]建立了一个跨期框架中的权衡模型，使用随机控制方法研究了DB计划中养老基金投资和缴费政策的优化。Davis等[5]通过对38个国家(16个新兴市场国家和22个OECD国家)养老金资产配置的实证分析，得出结论：将资产配置于股票可获得高投资回报率，对于OECD国家可以将少数比例的资产配置于国外资产，但投资国内股票可获得较高收益，且OECD国家不易将国外投资作为主要投资，养老金投资呈现“国内倾向”。肖建武等[6]通过构建养老基金资产配置的常方差弹性模型，提出了退休前后资产配置比例的计算公式，在追求指数效用最大化的条件下求得了精确解析解。对于具体养老金计划资产配置的研究多借助于数理模型的分析，如Gao[7]应用随机优化方法，构造了相应的Hamilton-Jacobi-Bellman偏微分方程，研究了DC计划养老基金的最优资产配置问题。

以上文献大都假设金融市场中只存在一种无风险资产和一种高风险资产(股票)，但是在现实应用中，可违约的公司债券也一直是保险公司的主要投资资产，因此考虑养老金基金在可违约债券上的投资也是很有必要的。Bielecki等[8]研究了在最大化终端财富的预期HARA效用的目标下，与违约债券相关的最优分配问题。Sun等[9]研究了模型歧义和违约风险下保险人的鲁棒最优投资和再保险问题，该问题包括储蓄账户、股票和违约债券的交易，目标是使期望CARA效用最大化。Deng等[10]推导出了具有违约风险的两个保险公司之间的非零和随机微分博弈的均衡策略。Jang等[11]同时考虑了借款约束和保险公司违约风险，解决了不完全市场中的最优消费和投资问题，以封闭形式推导出了最优消费和投资策略。

综合以上有关养老金计划最优投资问题的研究文献，目前还没有将违约风险与混合养老金计划结合起来的相关研究，因此本文的研究有一定的创新意义。本文模型受到Khorasanee[12]研究的混合养老金计划和Wang等[13]改进的计划的启发，结合DB和DC的资产负债相关研究，设计一个混合型养老金计划，对养老金缴款收入和养老金支出同时做出调整，以摊销因精算负债和基金价值之间的差异而产生的盈余或赤字，使得养老金风险可以由不同代人共同管理和分担。根据混合养老金系统的资产及负债情况，考虑违约风险因素，假设养老金资产可以投资于无风险资产、普通风险资产(如股票)和可违约债券，选择合适的目标函数进行投资策略的优化，分别得到违约前和违约后的价值函数和最优策略，从而动态调整养老金的缴费和收益水平，避免养老金计划中存在的不连续风险。最后对结果进行数值模拟，分析价格过程中相关参数对最优策略的影响。

本文的创新之处在于，将违约风险因素融入混合养老金计划的最优投资策略之中，这是对传统DB或DC型养老金计划研究的进一步深入，也是有关商业养老理财产品的理论创新。我国的养老保险金融改革刚刚起步，随着我国人口老龄化程度加深以及社会经济发展水平的提高，我国养老金体系三大支柱发展不均衡的问题日益凸显，加快养老金第三支柱建设迫在眉睫。为此，“十四五”规划纲要明确提出，要实现基本养老保险全国统筹，发展多层次、多支柱的养老保险体系；2021年9月3日，中国人民银行发布了《中国金融稳定报告(2021)》，提出规范发展第三支柱养老保险的建议；2021年9月10日，银保监会正式发布《关于开展养老理财产品试点的通知》，养老理财正式参与我国养老金第三支柱的建设。未来我国养老金第三支柱的发展前景广阔，考虑各种风险因素的养老金计划研究也是十分有意义的。

1 模型及假设

1.1 金融市场

给定赋流完备概率空间[Ω,F,(Ft)t∈[0,T],P]，Ω是真实空间，滤子Ft表示t时刻为止的所有信息，由m维标准布朗运动W(t)=[W1(t),W2(t),…,Wm(t)]′生成，且m维标准布朗运动Wi(t)之间相互独立，P是概率测度。假设在时间段[0,T]内，金融市场是一个无套利无摩擦的完全竞争市场，金融资产是连续交易的。

金融市场由一种无风险资产、一支股票(风险资产)和一种可违约债券组成，资产的价值满足：

dS0(t)=r0S0(t)dt,S0(0)=1,

(1)

dS1(t)=S1(t)[μ1dt+σ1dW1(t)],

(2)

式中，r0为无风险利率;μ1和σ1表示风险资产的风险溢价和波动率。

接下来推导违约资产的价格过程，不像前两种资产直接给出在现实世界概率测度P下的动态过程，我们首先定义风险中性概率测度Q下的价格过程，然后基于此给出概率测度P下的价格过程。令τ为违约时刻，它为定义在概率空间[Ω,F,(Ft)t∈[0,T],P]中的非负随机变量，则违约过程{H(t)}定义为H(t)=I{τ≤t}，假设该过程为概率测度P下具有恒定强度hP的泊松过程，则有鞅违约过程(3)，该过程为(G,P)鞅：

相对应的{Mp(t)}的随机微分方程为

dMp(t)=dH(t)-hp(1-H(t-))dt。

根据Bielecki等[8]的定义，存在一个到期日为T1的可违约零息债券，ζ∈[0,1]为违约发生时的损失比例(假设为常数)，hQ为测度Q下的违约强度，风险中性信用利差为δ′=ζhQ，则该违约债券的价格过程为

p(t,T1)=I{τ>t}e-(r+δ′)(T1-t)+I{τ≥t}(1-ζ)e-(r+δ′)(T1-t)er(t-τ)。

在测度Q下有类似的(G,P)鞅过程：

那么违约债券的价格过程满足：

dp(t,T1)=rp(t,T1)dt-ζe-(r+δ′)(T1-t)dMQ(t)。

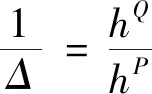
dp(t,T1)=p(t-,T1)[rdt+(1-H(t))(1-Δ)δ′dt-(1-H(t-))ζdMp(t)],

(3)

该方程由两个部分组成(Yu[15])：第一部分是相同条件无违约债券的收益；第二部分是t时没有发生违约的前提下风险中性信用利差与真实世界信用利差之间的差异。

1.2 混合养老金计划设定

考虑非平稳年龄结构人群在一个时间周期内的演化：

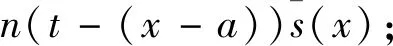
(3)w(x,t)表示a≤x≤r时在职人员的平均年薪率。假设达到退休年龄r的成员的初始养老金福利是当时最终薪金率的ξ部分，即工资替代率为ξ；

(4)h(x)表示适用于多年前退休人员(x-r)的初始养老金福利的年龄相关调整系数，且h(r)=1；

养老金计划的最终筹资方法可表示为t时刻r年龄退休人员未来养老金收入精算现值=工作期间应计养老金。t时刻r年龄退休人员未来养老金福利总额精算现值为

在职人员在t时刻达到退休年龄r时确认养老金负债(义务)，该负债需要通过在职成员在工作期间的缴款来确认和供资。为了描述养老金的应计精算负债，应用Bowers等[16]的精算函数M(x)来表示在职成员在终端供资方法下作为养老金系统精算负债累积的1美元未来养老金福利的一部分。M(x)为非减函数，对a≤x≤r，年龄为x的成员具有0≤M(x)≤1的右连续函数。定义M(x)的密度函数为m(x)，以密度m(x)累积的缴费可以完全提供给计划成员支付未来养老金。

用NC(t)代表t时所有在职成员未来养老金福利的精算现值比率，这也是t时需要由在职成员的养老金缴款供资的公认负债比率。

(4)

用PB(t)表示t时刻需向所有已退休人员支付的养老金比率：

(5)

由于存在着财务风险，养老金的盈利水平对养老金系统存在着一定的隐含性影响，因此，应该动态地调整在职成员目前支付的养老金缴款和应支付给退休人员的养老金支出。为了实现这个目标，定义两个控制变量λ1(t)和λ2(t)，用以同时调整养老金给付率(即养老基金收益)和缴费率(即养老基金支出率)。

B(t)=PB(t)+λ1(t),

(6)

C(t)=NC(t)-λ2(t),

(7)

式中，C(t)为养老金的缴费率，B(t)为养老金的给付率。若t时刻养老金基金存在着盈余SP(t)>0，那么就可以对λ1(t)和λ2(t)进行正向调整，即增加养老金给付，减少养老金缴费；若t时刻养老金基金存在着盈余SP(t)<0，那么就可以对λ1(t)和λ2(t)进行负向调整。这两个控制变量发挥着摊销养老金基金盈余SP(t)的作用，基金的资产回报分散在在职成员和退休人员身上，这就意味着代际之间的不连续风险可以根据基金盈余情况进行转移或分担，养老金计划的“混合性”也就体现在这里。

1.3 混合养老金资产负债过程

假设t时刻投资于股票和可违约债券的金额分别为π1(t)和πp(t)，则混合养老金的财富过程表示为

(8)

养老金计划中的实际总负债不仅包括精算应计负债，还应包含其他因素造成的负债，因此可以对精算应计负债进行修正，将投资收益的变化纳入负债的调整，从而得到实际负债的微分表达：

(9)

式(9)可以进一步转化为

(10)

因为SP(t)=F(t)-L(t)，则有盈余过程的微分方程：

(11)

设φ(t,l,f)为t时刻的目标函数，l为负债水平，f为资产价值，则有

(12)

(13)

式中，∏是所有可容许策略的集合，参数是估值的贴现率β和3个损失函数Lλ1(t)、Lλ2(t)和LSP(t)，它们分别代表收益风险、缴费风险和计划终端盈余的不连续风险。

2 模型求解

使用指数效用函数作为损失函数，度量收益风险、缴费风险、不连续风险的损失函数由指数函数组成：

Lλ1(t;Q1,q1)=Q1e-q1λ1(t),

Lλ2(t;Q2,q2)=Q2e-q2λ2(t),

Lsp(t;Q3,q3)=Q3e-q3sp(t),

式中，系数Qi为损失函数的相对权重，反映了退休人员的风险偏好。qi为相应正、负偏差的内部权重。一般情况下，指数型损失函数对负偏差的权值大于对正偏差的权重。价值函数最终表示为

F(t)=f,H(t)=z],

(14)

边界条件为J(T,l,f)=Q3e-q3SP(T)-βT。

使用标准随机控制方法为最优化问题提供框架。通过运用HJB变分法将完全非线性偏微分方程转化为常微分方程进而对该模型进行求解，最终得到最优投资策略。在本节中，首先利用随机最优控制理论推导出优化问题式(14)的一般框架，然后分别得到违约前(z=0)和违约后(z=1)的价值函数和最优策略。

2.1 一般框架

上述优化问题对应的HJB方程为

sup{Aπ,λ1,λ2J(t,l,f,z)}=0,

(15)

J(t,l,f)的变分算子为

Aπ,λ1,λ2J(t,l,f,z)=Jt+[r0f+π1(t)(μ1-r0)+πp(1-H(t))(1-Δ)δ′+C(t)-B(t)]Jf+

hp[J(t,f-ζπp,l,1)-J(t,l,f,0)](1-z)+[Q1e-q1λ1(t)+Q2e-q2λ2(t)]e-βt,

(16)

式中，Jt、Jl、Jf、Jff分别为变量t、l、f的一阶偏微分和二阶偏微分。

2.2 违约后情况(z=1)

在违约发生后，p(t,T1)=0，τ≤t≤T，那么有πp(t)=0。式(16)变为

Aπ,λ1,λ2J(t,l,f,1)=Jt+[r0f+π1(t)(μ1-r0)+πp(1-H(t))(1-Δ)δ′+C(t)-B(t)]Jf+

(17)

因此，基于最优控制问题式(15)，分别给出了最优资产分配策略和调整策略。

定理1 最优策略的控制变量为

(18)

相对应的值函数为J(t,l,f,1)=Q3e[b(t)f+c(t)l+h1(T-t)-βt]；其中，

2.3 违约发生前(z=0)

当违约没有发生时，有

(19)

因此，针对最优控制问题式(15)，分别给出了最优资产分配策略和调整策略。

定理2 最优策略的控制变量为

(20)

相对应的值函数为J(t,l,f,1)=Q3e[b(t)f+c(t)l+h0(T-t)-βt]。其中，

3 数值模拟与分析

上一节中，在指数效用函数下，得到了混合型养老保险模型的最优投资分配和养老保险费率以及养老保险福利支付调整策略的明确表达式。在这一部分，使用蒙特卡罗模拟方法来提供数值例子说明得出的结果。

3.1 基本数值假设

养老金模型中相关基础公式假设参考Bowers等[16]的研究；模型中的其他参数取值参考Wang等[13]和张永涛等[17]的研究，具体参数取值如表1、2所示。

表1 相关公式假设

表2 相关参数取值

3.2 模拟结果

(1)违约发生后。

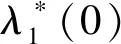
(2)违约发生前。

①模型参数对最优投资策略的影响。图5～7描述了资产组合中可违约债券的最优投资比例变化及相关参数的影响。总体来看，可违约债券的最优投资比例随着时间的推移而降低。由图5可知，可违约债券的最优投资比例与违约强度hp成反比，即违约强度越高，投资计划对可违约债券的投资金额越少；由图6可知，可违约债券的最优投资比例与违约损失率ζ成反比，因为当违约发生时，损失率越高，可违约债券就越没有吸引力；由图7可知，可违约债券的最优投资比率与风险中性信用利差δ′成正比，因为信用利差越大，増加对可违约债券的投资金额将获得更多的收益。

4 结论

本文主要研究了违约风险下混合养老金计划的最优投资和策略调整问题。假设养老金基金可以投资于一种无风险资产、一种普通风险资产(如股票)和一种可违约债券，考虑在职成员和退休人员的“损失”以及与养老基金连续性相关的终端约束的养老基金随机最优控制问题，根据动态规划原理，建立相对应的HJB方程，分别得到违约前和违约后养老金计划的最优投资策略和最优调整策略，最后通过数值模拟分析了各模型参数对最优策略的影响。结果显示在职人员和退休人员对损失的厌恶程度会影响到最优缴费调整策略和最优收益调整策略；风险资产模型和可违约债券价格模型中的参数都会影响对风险资产和可违约债券的投资策略，研究得出相关参数对投资策略的影响也可以为养老金计划或政策的设计提供借鉴。党的十八大以来，政府高度重视养老金第三支柱的发展，在第一支柱养老金基本完善，第二支柱职业养老金覆盖面不足的背景下，逐渐强调规范发展养老保险第三支柱，第三支柱的建设方向逐渐明确，我国养老理财市场将迎来巨大发展空间，对养老金计划的投资问题进行研究，有助于养老理财产品的设计和规划。

本文假设违约强度是恒定的常数，但是在实际问题中，违约强度往往是一个不确定的动态变化过程，以随机过程或相关分布来刻画违约强度可能更合理一些，如Jang等[11]就为违约强度设计了一个密度函数，使用分布函数来刻画违约过程。此外本文以期望指数损失效用最小为目标建立目标函数，使用其他形式的效用函数是可以进一步延伸的研究方向。