植被指数模型估算干旱区稀疏光合/非光合植被覆盖度

骆义峡，姬翠翠，，李晓松，徐金鸿，杨雪梅

(1.重庆交通大学，重庆 400074；2.中国科学院遥感与数字地球研究所，北京 100094；3.甘肃省治沙研究所，兰州 730070)

0 引言

干旱和半干旱地区占我国国土面积的53%。由于土地荒漠化日剧严重，干旱和半干旱区植被在防风固沙、调节生态平衡等方面具有重要作用，植被的退化严重影响绿洲的生态安全[1]，因此，干旱区稀疏植被指标定量评价对科学评估土地荒漠化及其治理效果评估具有重要的意义[2]。

目前，针对光合植被(photosynthetic vegetateon，PV)和非光合植被(non-photosynthetic vegetation，NPV)覆盖度定量估算已有一些研究，但是大部分研究主要集中于光合植被覆盖度(fractional cover of PV，fPV)[3]，而非光合植被覆盖度(fractional cover of NPV，fNPV)[4]的估算起步较晚，相关研究较少，同步获取fPV、fNPV的研究更少[5]。单一的光谱指数，如表征PV的归一化植被指数(normalized difference vegetation index，NDVI)、表征NPV的干枯燃料指数[6](dead fuel index，DFI)只适用于混合像元由光合植被与裸土(bare soil，BS)或NPV与BS两种成分组成，当同时估算PV、NPV和BS三端元的比例，使用单一光谱指数估算fPV、fNPV存在一定局限性[7]。混合像元分解是估算干旱区稀疏植被覆盖度的有效方法，经前人研究所得线性光谱混合模型以及像元三分模型能够有效估算fPV、fNPV，且具有物理意义明确、计算简便的优势。

目前植被覆盖度估算研究中，多数研究基于光学遥感数据，其中高光谱数据获取困难，且成本较高。因此，本文采用Sentinel-2A多光谱数据，考虑光合植被独有的特征(叶绿素及红边效应)，选取优化的叶绿素吸收指数[8](modified chlorophyll absorption ratio index，MCARI)和红边叶绿素指数[9](red-edge chlorophyll index，CIred-edge)表征光合植被，以甘肃民勤绿洲为研究区分别建立NDVI-DFI、MCARI-DFI、CI-DFI像元三分模型。同时，构建基于NDVI、DFI、比值土壤指数(ratio soil index，RSI)的线性指数模型，开展服务于PV/NPV覆盖度估算的最佳线性指数混合模型研究。为此，本文基于地面控制性实验获取纯净端元光谱与端元丰度信息，选择不同光谱指数组合建立三分模型，评价各指数组合的三分模型性能，在最优三分模型中加入RSI构建线性指数模型，评价其在PV/NPV覆盖度估算的精度，为PV/NPV覆盖度估算提供更可靠的理论方法。

1 研究区概况

实验区位于甘肃省武威市民勤县绿洲-荒漠过渡带区域内(38°37′42.60″N，102°55′11.25″E)，该区域的面积为22.8 km2，主要由沙漠、低山丘陵和平原3种基本地貌组成，温带大陆性干旱气候区，大陆性沙漠气候明显，冬冷夏热，降水稀少，光照充足昼夜温差大，年均降水量113.2 mm，年均蒸发量2 675.6 mm。受地理位置及气候影响，土地荒漠化十分严重，其自然植被主要由白刺灌丛、梭梭等几种典型的荒漠植被所构成，PV/NPV及BS镶嵌景观广泛存在[10]。

2 数据与方法

2.1 Sentinel-2A数据获取

Sentinel-2A(S2A)数据是从Sentinels科学数据中心(https：//scihub.copernicus.eu/)下载的经过正射校正和几何校正的L1C级多光谱数据，成像时间为2016年7月25日。S2A数据共有13个波段，最高空间分辨率为10 m，是红边范围内唯一含有3个波段的光谱数据源，能够更好地监测植被的健康信息。

对S2A数据的预处理工作，使用ESA官方发布的Sen2cor v2.8插件处理L1C级数据，得到经过辐射校正和大气校正的L2A级数据。由于研究中使用了空间分辨率为10 m和20 m的部分波段，因此需要将空间分辨率为20 m的波段重采样为10 m。

2.2 野外实测获取

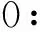
2.3 参考端元丰度获取

为评价模型精度，2016年8月在研究区选取了111个样地开展野外观测工作，分别获取每块样地PV和NPV的植被覆盖度信息，同时利用全球定位系统记录每个样地在WGS84坐标系下的中心位置。植被覆盖度信息测量采用针刺法(间隔1 m)，实际测量时，对于自然植被群落(图1(b))，采用3个30 m测量带交叉布置，测量带两两之间夹角为60°(图1(a))；对于平行排列的人工植被(图1(d))，采用2个30 m的测量带，相互垂直布置并与平行植被交叉角为45°(图1(c))。观测者记录每米的物质类型，包括绿叶、隐花植物、凋落物以及不同类型的裸土。如果有中层(灌木)或上层(树木)植被则利用仪器记录顶层覆盖率。当记录的植被仍然附着叶片时，则记录人员应按照叶片颜色判断植被是否为光合植被。

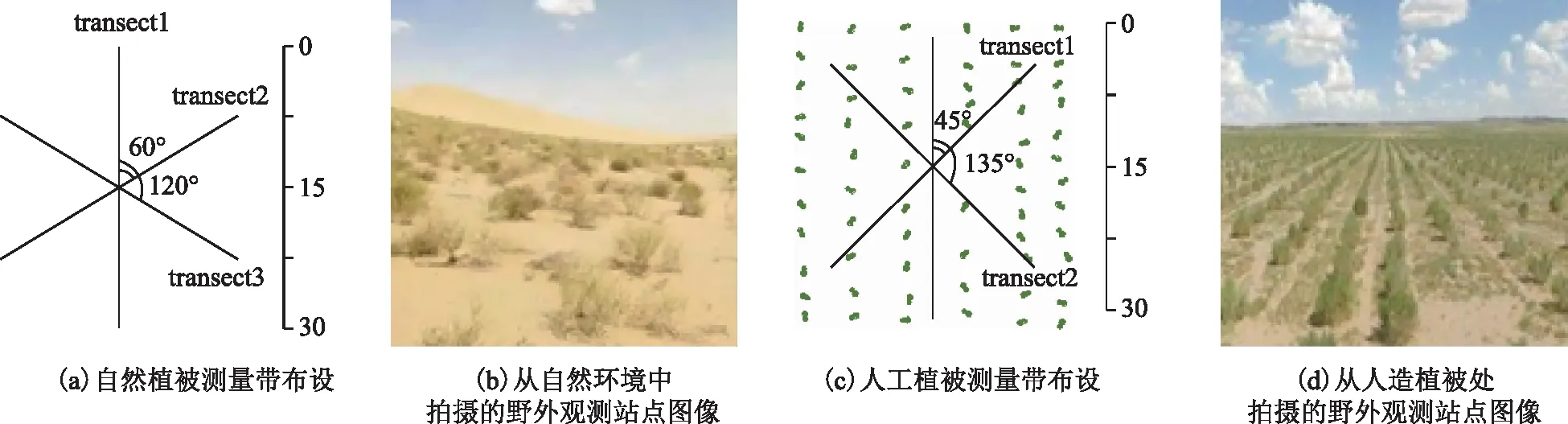
图1 现场测量带布设

3 研究方法

3.1 光谱指数

1)NDVI。NDVI是利用光合植被对于红、蓝光的高吸收以及对绿光与近红外的高反射这一独有特性提出的。NDVI值取值范围在-1～1之间，当NDVI值为负值是表示地表被水体、雪、云等覆盖；土壤的NDVI值一般都为0，因为土壤在近红外与红光波段值近似相等；NDVI值为正值时表示地表有植被覆盖，且植被覆盖度与NDVI值呈正相关。

2)红边叶绿素指数(CIred-edge)。红边叶绿素指数是PV在680～750 nm波长范围内受到叶绿素和细胞结构等因素影响，光谱曲线表现出明显的波峰和波谷现象，致使PV有着明显的红边光谱特征，且岩石、土壤和大部分凋落物并不存在该特征。

3)MCARI。叶绿素作为PV的独有特征，因此叶绿素含量能够有效地将PV从NPV、BS背景中区分开来。MCARI是基于高光谱数据提出的光合植被指数，利用550、700、750 nm 3个波段估算叶绿素含量效果更好，但是S2A多光谱数据未采集波长为750 nm的反射值，经研究发现，基于S2A多光谱数据的band 3、band 4和band 8构建的MCARI指数能够很好地估算植被叶绿素含量。

4)DFI。DFI是总结NPV和BS在MODIS影像中的光谱特征提出的。本文总结NPV和BS在S2A影像中的光谱特征，发现在S2A影像与MODIS影像中NPV和BS有着相似的光谱特征：NPV与BS在665 nm(band 4)和842 nm(band 8)处的光谱曲线变化较于平缓，且反射值大于PV；在1 610 nm(band 11)附近PV与NPV出现波峰，BS反射值呈缓慢持续增长；在2 190 nm(band 12)附近PV与NPV出现波峰，BS出现波谷。

5)RSI。RSI是根据BS在S2A多光谱数据中的光谱特征曲线总结得出的表征土壤的指数。BS在665 nm(band 4)到842 nm(band 8)反射值增长相对于PV和NPV较小，且呈缓慢变化趋势；在2 190 nm(band 12)处的反射值大于1 610 nm(band 11)处的反射值，且PV与NPV在2 190 nm(band 12)处的反射值小于1 610 nm(band 11)处的反射值。因此，总结出基于S2A多光谱数据的RSI，如式(1)所示。

(1)

式中：B4、B8、B11、B12分别代表S2A第4波段(red)、第8波段(NIR)、第11波段(SWIR)和第12波段(SWIR)。

3.2 像元三分模型

像元三分模型[11]是在端元已知的情况下，假定混合像元由PV、NPV以及BS 3个成分组成，通过线性模型来分解混合像元。理想情况下，影像的二维特征空间会表现为三角形，且所有混合像元的PV、NPV和BS理论上都分布在该三角形内，如图2所示。

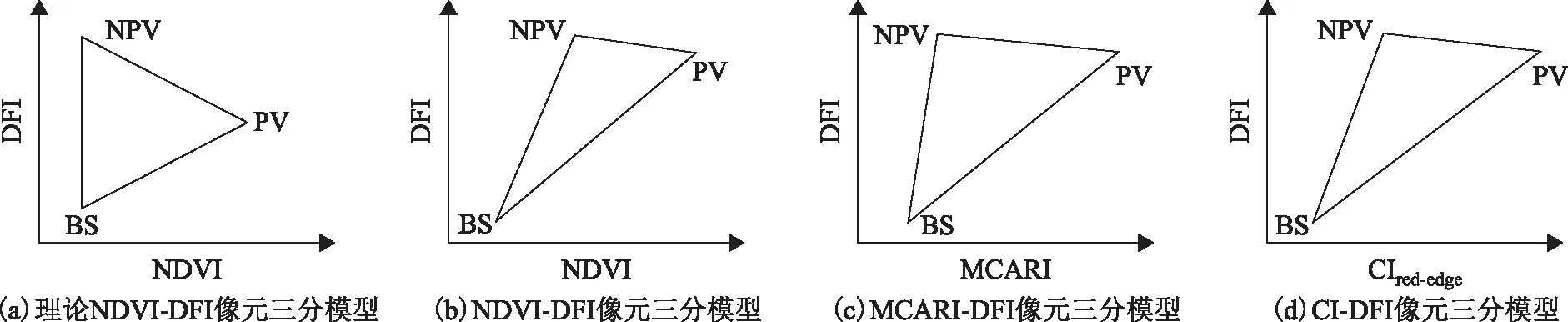
图2 像元三分模型

如图2所示，本文构建的NDVI-DFI、MCARI-DFI、CI-DFI 3个像元三分模型其二维特征空间均表现为三角形，符合像元三分模型的基本假设，且与理论上的基本概念一致。由图2(a)可知，在理论上的像元三分模型中PV端元的NDVI值最大；NPV端元的NDVI与BS相近，DFI值最大；BS端元的NDVI值与DFI值均为最小；图2(b)、图2(c)、图2(d)是依据地面控制性实验测得纯净端元光谱计算得到。

3.3 线性指数模型

线性指数模型是像元三分模型在应用上的延伸，结合线性光谱混合模型的思路，由多光谱数据计算得到的指数替换影像波段，建立线性模型，分解像元得到各个端元覆盖度的方法。本文使用的线性指数模型是在NDVI-DFI像元三分模型的基础上加入RSI指数建立的线性指数模型，由式(2)至式(5)所示。

N=∑fiNi=fPVNPV+fNPVNNPV+fBSNBS

(2)

D=∑fiDi=fPVDPV+fNPVDNPV+fBSDBS

(3)

∑fi=fPV+fNPV+fBS=1

(4)

R=∑fiRi=fPVRPV+fNPVRNPV+fBSRBS

(5)

式中：N代表S2A数据的NDVI值；D代表S2A数据的DFI值；R表示S2A数据的RSI值；NPV/DPV/RPV、NNPV/DNPV/RNPV、NBS/DBS/RBS分别表示PV、NPV与BS的NDVI、DFI与RSI端元特征值；fPV、fNPV、fBS分别代表像元内PV、NPV和BS的占比。

4 结果分析

4.1 像元三分模型获取fPV和fNPV结果分析

基于研究区的NDVI、MCARI、CIred-edge以及DFI指数，绘制NDVI-DFI、MCARI-DFI、CI-DFI特征空间(图3)，特征空间均呈现出PV端元的NDVI、MCARI以及CIred-edge值较高；NPV端元的DFI值较高且NDVI、MCARI以及CIred-edge值较低；BS端元的NDVI、MCARI、CIred-edge以及DFI值均比较低。

在模型的特征空间图中，值得注意的是，3个像元三分模型的特征空间均表现为三角形。由图3可知，大部分像元主要集中在BS端元，表明研究区内裸土占比极高、植被覆盖度低，与干旱区沙漠边缘地带植被覆盖度低的实情一致。前人研究证明,NDVI指数能够准确地表达植被生长情况[12]，在NDVI-DFI特征空间中PV端元少部分像元集中，反映出民勤绿洲植被情况良好。研究表明，民勤绿洲植被每年7、8月植被情况最好，该特征空间PV端元信息符合实情。因此，相较于MCARI-DFI、CI-DFI模型，NDVI-DFI模型的特征空间与PV/NPV时空分布最为相似。为了对NDVI-DFI、MCARI-DFI、CI-DFI构建各三分模型在估算fPV和fNPV性能上进行评价，构建模型并求解对应的端元丰度，同时利用实地测量端元丰度信息进行fPV和fNPV的精度评价。NDVI-DFI模型对fPV和fNPV估算的RMSE分别为0.059 0和0.051 0；CI-DFI模型对fPV和fNPV估算的RMSE分别为0.081 3和0.054 6；MCARI-DFI模型对fPV和fNPV估算的RMSE分别为0.085 9和0.059 6；NDVI-DFI模型相较于MCARI-DFI、CI-DFI模型表现出更好的估算效果，fPV和fNPV的估算精度最大提高了31.3%和14.4%。根据端元丰度散点图(图4)，NDVI-DFI模型估算结果更接近实测端元丰度，其中fPV散点位置分布均匀，且大部分点位于参考线(X=Y)附近，对于NPV，稀疏NPV覆盖度的估算值分布均匀，且大量点位于参考线附近，随着NPV覆盖度的增加估算误差变大；MCARI-DFI、CI-DFI模型的估算结果出现严重的堆积现象，估算值大量位于0附近。因此，本文采用NDVI-DFI模型估算fPV和fNPV的结果精度较其他两个模型精度更高，结合端元丰度验证散点分布，表明基于NDVI-DFI像元三分模型估算民勤绿洲稀疏植被覆盖度是可行的。

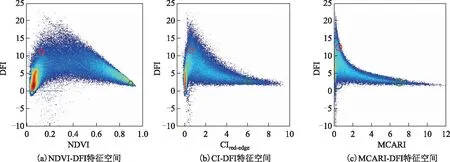
注：绿色、红色和蓝色圆圈分别代表PV、NPV和BS端元的位置。图3 特征空间

根据3个模型估算与实测fPV和fNPV散点图(图4)来看，fPV的估算在3个模型中均表现出低估现象，fNPV的估算均表现出高估现象，主要是由于像元三分模型在枯黄期对fNPV敏感，然而DFI与叶片含水量以及叶绿素含量密切相关，且每年7、8月为雨季生长期，因此PV与NPV的DFI值相对于其他时期相对较低且PV与NPV的相互重叠。成熟的理论基础以及遥感技术的估算结果还是相对可靠的，NDVI-DFI像元三分模型的估算结果也验证了这一结论。

图4 像元三分模型估算fPV和fNPV精度分析图

4.2 线性指数模型获取fPV和fNPV结果分析

从4.1节得知，NDVI-DFI构建三分模型对PV和NPV覆盖度获取相对其他两个指数具有更强的敏感性，因此本节在NDVI-DFI三分模型基础上加入RSI指数，构建NDVI-DFI-RSI的线性指数模型，由式(2)至式(5)联立组成4个方程，解算3个端元覆盖度。如图4所示，线性指数模型的精度分析图与NDVI-DFI像元三分模型精度分析图基本一致，但是线性指数模型的散点分布更加聚合，部分估算值更加接近实测值，线性指数模型估算fPV的RMSE为0.052 4，估算fNPV的RMSE为0.044 4。由以上结论可知，RSI指数的加入可以有效提高fPV和fNPV估算精度，将NPV/PV中BS误分的部分有效分离，本文构建线性指数模型能够提高干旱区稀疏植被覆盖度估算精度。

4.3 线性指数模型与像元三分模型比较分析

像元三分模型属于线性指数模型，都是通过指数与覆盖度之间的线性关系求解fPV、fNPV和fBS。本文线性指数模型相较于像元三分模型增加土壤指数RSI参与建模，提高土壤在模型中的辨识度，以减少BS的误分几率。从绘制散点图4(a)、图4(d)来看，与NDVI-DFI像元三分模型fPV和fNPV估算精度散点分布图比较，线性指数模型估算结果与实测结果相关性略有提高，且其散点分布更贴近于参考线(X=Y)，一定程度上缓解了PV的低估现象和NPV的高估现象。其次，从4.1节与4.2节得知，线性指数模型估算精度要优于像元三分模型，fPV和fNPV的估算精度分别提高了11.2%和12.9%。可见，将土壤指数RSI引入NDVI-DFI三分模型中能够有效将BS从PV与NPV中分离出来，提高fPV和fNPV的估算精度。针对线性指数模型，指数与指数数量的正确选择对fPV和fNPV估算精度的影响是不可忽略的。

5 讨论

5.1 NDVI在干旱区的应用潜力

总结前人研究，像元三分模型利用多个波段计算指数，减少了端元光谱异质性以及影像质量等引起的误差，有助于fPV、fNPV的估算[13]，且已有研究结果表明，无论是基于高光谱的像元三分模型(NDVI-CAI)还是基于多光谱的像元三分模型(NDVI-DFI)均能够有效估算fPV和fNPV[14-17]。但是，像元三分模型受到指数与端元的关系、纯净端元提取、影像质量等因素的影响。本文利用MCARI、CIred-edge与DFI构建像元三分模型，得到的估算精度与NDVI-DFI三分模型估算精度具有较大差异，分析其原因可能主要是受到指数适用性的限制以及植被冠层结构不同的影响。经研究证实，NDVI与fPV呈线性关系[18-19]，DFI与fNPV呈线性关系[20-21]，结合4.1节实验结果证明，NDVI-DFI像元三分模型能够较好地估算fPV和fNPV。尽管MCARI能够较好地估算叶绿素含量，同时叶绿素含量与光合植被覆盖度之间具有很强的相关性[22]，但是MCARI对背景反射特性非常敏感，在低叶面积的情况下难以获得较好的估算结果，不适用于稀疏植被的覆盖度估算[23]。同样，CIred-edge与植被叶绿素、氮含量具有显著的线性关系[24]，但是该指数对叶绿素含量估算受到土壤湿度以及光照的影响[25]且表现出一定的地域性，估算效果不稳定[26]。同时，MCARI、CIred-edge都是基于小麦、油菜等构建的，其冠层特征与干旱区植被冠层差异较大，因此可能导致估算效果不理想，其在干旱区植被覆盖度的估算效果还有待进一步验证。

5.2 土壤指数

在传统的植被指数构建理论中，考虑土壤影响并加以削弱，能够提高植被指数对植被的敏感性[27]。Towers[28]、Xie等[29]基于考虑土壤因素的植被指数建立了关于LAI的最佳估算模型，有效提高估算精度。本研究基于线性混合像元分解理论，引入土壤指数，通过对比像元三分模型与线性指数模型估算fPV和fNPV发现，拥有土壤指数的线性指数模型的估算精度相对于像元三分模型略有提高，成功地将BS误分为PV与NPV的部分分离出来，从而提高fPV和fNPV估算精度。同样，本文线性指数模型是像元三分模型改进而来，同样存在像元三分模型的局限，因此，增加的指数与端元覆盖度之间有无线性关系影响着线性指数模型的估算结果。线性指数模型增加的RSI指数是总结Sentinel-2A的地物光谱特征曲线，表征土壤信息，该指数与土壤是否存在显著的线性关系，有待进一步研究确定。在未来基于线性指数模型估算稀疏植被覆盖度时，如何更好地选择建模指数、参与建模指数数量以及纯净端元的确定将会是一个重要的研究方向。

6 结束语

本文基于对植被具有明显特征优势的Sentinel-2A多光谱数据，结合地面控制性实验获取纯净端元丰度和实测端元丰度信息，分别构建NDVI-DFI、MCARI-DFI、CI-DFI像元三分模型以及NDVI-DFI-RSI线性指数模型，寻求适合PV/NPV覆盖度估算的最佳像元混合模型，探索线性指数模型在PV/NPV覆盖度估算上的适用性。经研究得出以下结论。

1)植被指数NDVI-DFI、MCARI-DFI、CI-DFI特征空间均表现为三角形，符合像元三分模型构建的基本条件，因此本文构建了基于NDVI-DFI、MCARI-DFI、CI-DFI指数的像元三分模型，实现了干旱区稀疏PV/NPV覆盖度估算。

2)参考构建3个像元三分模型精度来看，CI-DFI模型，fPV估算的RMSE为0.081 3(R2=0.550 5)，fNPV估算的RMSE为0.054 6(R2=0.651 7)；MCARI-DFI模型，fPV估算的RMSE为0.085 9(R2=0.552 1)，fNPV估算的RMSE为0.059 6(R2=0.654 3)；NDVI-DFI模型相较于MCARI-DFI、CI-DFI模型表现出更高的估算精度，fPV估算的RMSE为0.059 0(R2=0.773 8)，fNPV估算的RMSE为0.051 0(R2=0.8)。

3)在NDVI-DFI模型中融入RSI指数构建的线性指数模型可以提高fPV和fNPV的估算精度，fPV估算的RMSE为0.052 4(R2=0.776 4)，fNPV估算的RMSE为0.044 4(R2=0.811 5)，精度分别提高约11.2%和12.9%。因此，融入RSI指数的NDVI-DFI线性植被指数模型可以有效地提高估算稀疏植被的fPV和fNPV，为NPV覆盖度估算精度的提高提供更可靠的理论基础。