软基水闸底板脱空反演中的传感器优化布置方法

李火坤，方 静，黄 伟，万子豪，涂 源,刘双平

(南昌大学工程建设学院，江西 南昌 330031)

目前，我国已建成的水利枢纽工程位居世界第一，水闸是水利枢纽的重要组成部分，其长期服役于复杂和特殊的工作环境，易产生各种病患，而闸基病患是影响水闸安全的重要因素之一。闸基底部在上、下游水位差的作用下，会产生强渗透带和闸基脱空区，从而导致水闸坍塌事故，如福清市棉亭盐场水闸曾在1984年发生闸基渗漏引起底板掏空，使闸室产生倾斜和裂缝；福清市海口前村水闸曾在2006年发生闸基渗漏导致水闸底板严重掏空，造成下游护坦、消力池和边墙坍塌等。因此，加强水闸底板运行状态的安全监测，实现对水闸健康状况的实时监测，对保证水闸的长期安全运行具有重大意义。基于模态参数的水闸底板脱空监测方法可在无损条件下识别底板脱空的范围和程度，很好地实现对水闸底板脱空区域实时监测，以便及时采取补救措施，减少人力和财力的损失[1-4]。在水闸底板脱空监测环节中，传感器系统是最重要的一个环节，传感器的布置不仅直接影响结构动力特征参数测试的精度，更是水闸底板脱空区域识别成功与否的关键一步。现有的水闸传感器布置方法以工程经验为主，缺乏理论支撑，因此系统构建水闸传感器优化布置方法具有重大意义[5-6]。

近年来，国内外学者针对结构监测中的传感器优化布置方法做出了大量研究，Cobb等[7]最早以结构损伤可识别为目的进行了传感器优化布置研究，探究了结构损伤对模态参数的影响，确定模态信息是限制结构损伤识别程度的关键因素。Vincenzi等[8]基于信息熵理论考虑了框架与桥结构中模态误差的影响，将距离和模态预测误差相关性矩阵作为目标函数实现传感器优化布置的综合性能，用于解决桥梁振动中的传感器优化布置问题。李火坤等[9]提出了一种结合QR分解(正交三角分解)和MAC准则(模态置信度准则)的逐步累积法，用于解决泄流激励下高拱坝振动测试中的传感器布置问题。吴子燕等[10]结合有效独立法和运动能量法，提出了有效独立-驱动点残差法的优化布置方法，用于解决桁架结构的传感器布置问题。谢强等[11]提出了一种基于模型减缩和线性模型估计理论的传感器优化布置方法，用于解决建筑结构中的传感器布置问题。滕军等[12]提出了基于模态能量和自适应遗传算法的传感器优化布置方法，用于解决大跨空间结构中模态测试时的传感器优化布置。范恒承等[13]融入多能量参数对有效独立法进行改进，用于空间桁架结构监测中的传感器布置问题。高博等[14]提出了一种基于模态置信度准则的自适应引力算法，用于解决桥梁监测中的传感器布置问题。

综上所述，软基水闸底板脱空反演中的传感器优化布置研究不多，本文提出了一种结合有效独立法(effective independence，EI)和损伤灵敏度法(damage sensitivity，DS)的传感器优化布置方法，同时采用模态柔度及节点相似度改善测点敏感性和模态冗余度，以Fisher信息矩阵2-范数最大为目标实现测点优化，并将该方法运用于软基水闸底板脱空反演，通过比较测点优化前后的MAC矩阵非对角元素最大值和软基水闸底板脱空区域识别结果以验证该方法的有效性，以期能为软基水闸底板脱空检测传感器优化布置提供参考。

1 软基水闸底板脱空传感器优化布置方法

1.1 EI-DS法

一个自由度为n的动力系统无阻尼自由振动方程为

(K-λiM)Φi=0

(1)

式中：K为刚度矩阵；M为质量矩阵；λi为系统的第i个特征值，即第i阶模态频率；Φi为特征向量，即第i阶模态振型。

根据摄动有限元法，假设损伤时结构的刚度只发生扰动，不考虑阻尼和质量的变化，则系统振动方程可表示为

[(K+ΔK)-(λi+Δλi)M](Φi+ΔΦi)=0

(2)

式中ΔK、Δλi、ΔΦi分别为结构刚度、特征值和特征向量的变化值。

忽略二阶项[16]，式(2)可表示为

(K-λiM)ΔΦi=ΔλiMΦi-ΔKΦi

(3)

由于各阶模态相互独立，则第i阶模态振型的变化量ΔΦi表示为原系统模态振型的线性组合：

(4)

式中：dik为第k阶模态振型的振型变化参与系数；n为模态总数。

(5)

根据振型的正交化原理，由式(5)可得

(6)

(7)

假定损伤后的结构刚度为每个单元刚度矩阵乘以损伤系数的总和，则单元刚度的变化为

(8)

式中：N为结构单元总数；Kl和αl分别为第l个单元刚度矩阵和损伤系数。

将式(8)代入式(7)，第i阶模态振型的变化可表示为各损伤对结构模态振型贡献的总和：

δA={α1α2…αN}

式中：F(K)为第i阶模态对结构损伤的灵敏度；δA为各单元损伤向量。

根据模态叠加原理可知，结构出现损伤后的动力响应为

us=(Φ+ΔΦ)q+k′=

(ΦF(K))(qεq)T+k′=Sθ+k′

(10)

其中θ=(qεq)T

S=(ΦF(K))ε=diag(ΔAi,…,ΔAi)

式中：ε为对角矩阵；q为模态向量坐标；k′为高斯白噪声；S为灵敏度矩阵。

在实际结构测试中，不能保证所有候选点都布置传感器，为使有限个传感器获得尽可能多的线性无关的振动数据，需要获得θ的最佳状态估计。根据协方差矩阵最小获得模态坐标θ的无偏估计，则待识别参数估计偏差的协方差矩阵为

(11)

式中Q为Fisher信息矩阵，Q=STS，当Q取极大值时可使P最小，θ就能获得最佳无偏估计。

当不考虑各自由度对结构损伤的灵敏度信息时，信息矩阵为ΦTΦ，即有效独立法[15]中的Fisher信息矩阵；若只考虑结构损伤对模态的影响，则信息矩阵为F(K)TF(K)，即损伤灵敏度法[16]中的灵敏度信息矩阵。因此，信息矩阵Q不仅反映了自由度对目标模态线性独立的贡献，同时包含了对结构损伤的灵敏度信息。

1.2 模态柔度

1.3 节点相似度及模态置信准则

对于大型结构，节点繁多会造成模态测试数据的冗余问题，因此引入两节点模态向量的相似度降低数据冗余程度，两节点模态向量的相似度函数参考文献[22]，如果两节点模态向量的差异度很小，则两节点模态向量的相似度值接近1，反之，如果两节点模态差异度很大，则两节点模态向量的相似度值接近0。同时，本文采用模态置信度准则(MAC)反映两个空间向量的相关性，MAC矩阵的非对角元素表示不同模态向量的交角情况，非对角元素越小，反映的结构特性越强，MAC矩阵的表达式参见文献[22]。

1.4 软基水闸底板脱空传感器优化布置步骤

a.利用ANSYS计算水闸底板脱空前后的频率和振型，计算水闸底板脱空前后各自由度的模态柔度。

c.采用节点相似度函数计算ΔHjj最大的节点与周围节点的相似度，将相似度较大的节点确定为同一区域，然后按照模态柔度变化率的排序依次类推进行分区，且每个区域中模态柔度变化率最大节点为传感器的初始选取测点。

d.构造信息矩阵Q，并在所选初始测点中以信息矩阵Q的2-范数最大作为优化目标[23]，从而确定传感器的数量。

2 算例验证

2.1 软基水闸有限元模型

图1 软基水闸有限元模型

为验证本文水闸底板脱空传感器优化布置方法的可靠性，以某工程为背景，建立了软基水闸有限元模型，如图1所示，模型比例为1∶10，水闸底板顺水流方向长1.44 m，垂直水流方向宽1.36 m，水闸底板厚度为0.16 m，闸墩高为1.6 m，厚0.16 m。选用solid65单元建模，有限元模型所选取的材料参数参考文献[24]。

表1 软基水闸底板脱空工况及脱空参数 单位：m

2.2 传感器优化布置方案

振动传感器不能布置于结构水下部位，故本文只考虑左右闸墩内侧大约1/5以上为传感器可布置区域，并通过闸墩的模态参数变化反映水闸底板脱空情况。两侧闸墩共有2 170个节点可布置，每个节点有3个自由度(分别为x、y、z)，即水闸的振动有x、y、z共3个方向，具体方向见图1中三维坐标轴方向。由于模态柔度对低阶模态较为敏感，且与频率的平方成反比，因此本文选择前两阶模态柔度作为目标进行测点优化布置，软基水闸低阶振型主要是两侧闸墩的纵向振动，因此只考虑水闸的纵向振型(y方向)，考虑到水闸结构节点繁多且距离相近，采用模态柔度和节点相似度函数进行传感器优化布置的初始选点，设置两种单侧脱空工况和一种相对侧脱空工况进行传感器优化布置，水闸底板脱空示意图如图2所示，本文通过ANSYS软件设置水闸底板脱空参数di(i=1,…,n)并将di线性连接来控制脱空区域的范围，共设置3种脱空工况，各工况水闸底板脱空参数理论值见表1[24]。

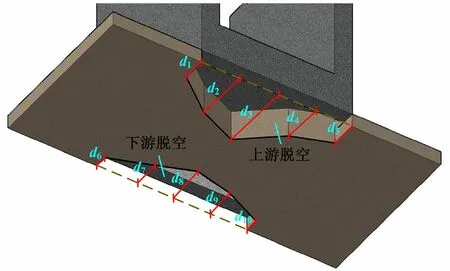
图2 软基水闸底板脱空示意图

图3 水闸底板未脱空时振型云图

利用ANSYS对水闸各工况进行模态分析，得出水闸底板未脱空时模态振型云图(图3)，其前两阶振动频率分别为22.739 Hz和24.366 Hz。根据频率和振型计算可测点的模态柔度并按水闸底板脱空前后可测点的模态柔度变化率的大小进行排序，然后对模态柔度变化率最大的测点采用节点相似度函数计算与周围测点的相似度，选取相似度大于0.5的测点作为区域1，再对区域1外的可测点模态柔度变化率进行排序，区域2～20的分区计算方法均与区域1相同，每个区域内模态变化率最大的测点为可选初始测点。水闸为对称结构，则左右闸墩分区相同，如图4所示，限于篇幅，只给出区域1～4各节点与模态柔度变化率最大节点的模态相似度，如图5所示。

图4 右侧闸墩分区

图5 各区域节点与模态柔度变化率最大节点间的模态相似度

由图5可知，节点模态向量相似度均大于0.5，说明区域内的节点模态均可达到同样的监测效果。本文根据各区域模态变化率最大节点的排列顺序选取前20个测点作为优化后的初始测点，并将最终优化布点的结果与从所有可测点中随机选取20个测点结果进行对比。各工况初始测点的传感器编号按其重要性排列结果以及随机选取的测点见表2，表2中测点编号对应的闸墩所在位置如图6所示，结合有效独立法-损伤灵敏度法，初始传感器布点编号对应的Fisher信息矩阵的2-范数变化趋势如图7所示。根据Fisher信息矩阵2-范数的变化趋势可知，对于工况一和工况二，选取前14个编号作为传感器布点；对于工况三，选取前20个编号作为传感器布点。则3种工况优化后的测点布置如图8所示。根据模态置信度准则，3种工况随机选取的测点MAC矩阵非对角元素最大值分别为0.999 8、0.578 3、0.167 9，优化后的MAC矩阵非对角元素最大值分别为0.272 7、0.196 2、0.131 5，由此可见，优化后的MAC矩阵非对角元素最大值均有降低。

表2 各工况随机选取和优化后传感器位置对应的节点号

图6 传感器编号对应的分布位置

图7 Fisher信息矩阵的2-范数变化趋势

图8 优化后的测点布置

2.3 软基水闸底板脱空反演结果验证

基于传感器位置随机选取以及优化后的传感器布置进行软基水闸底板脱空动力学反演对比验证，具体软基水闸底板脱空动力学反演过程可参考文献[24]。本文在反演过程中的模态参数采用模态柔度，传感器随机选取以及优化后各工况反演得到的软基水闸底板脱空参数与有限元模型底板脱空参数实际值对比结果及相对误差如见表3。为了使结果更直观，不同工况下脱空参数反演识别值与实际值对比如图9所示。采用随机选取测点以及优化后水闸底板脱空参数及脱空区域面积反演识别值与实际值的相对误差值为评价指标，各工况传感器优化布置前后脱空区域面积识别的相对误差值见表4。

结果表明，结合有效独立法和损伤灵敏度法可使水闸底板脱空参数识别值相对误差的平均值降低至15.9%，脱空识别面积相对误差减小到5%以内，

表3 不同工况优化布置后脱空参数反演结果及相对误差

图9 不同工况下脱空参数识别值与实际值对比

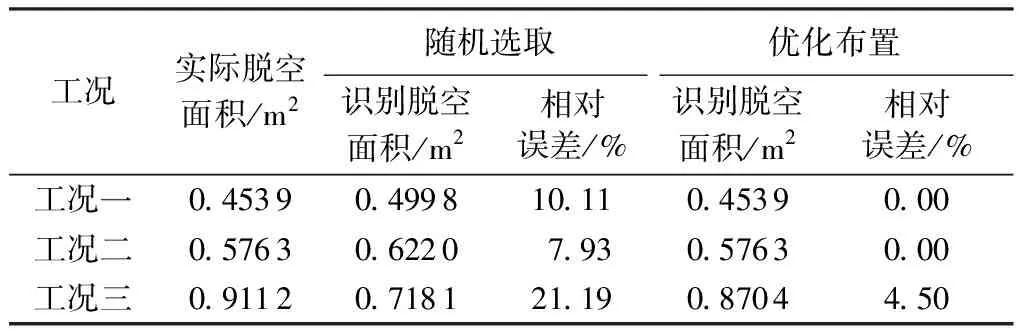
表4 反演识别脱空面积与实际脱空面积相对误差

达到很好的底板脱空反演效果，同时初始测点的选取验证了模态柔度对底板脱空相对敏感，从优化后所选点的MAC矩阵非对角元素值来看，此方法在保证底板脱空识别的同时，也可以使MAC矩阵的非对角元素值较小，满足模态置信度准则，验证了本文方法的有效性和可行性。

3 结 论

a.本文提出的结合有效独立法和损伤灵敏度法的多目标传感器优化布置方法，可同时包含模态线性独立信息和损伤灵敏度信息。

b.考虑节点模态数据冗余性，确定模态柔度为软基水闸底板脱空敏感特征量，同时引入节点相似度函数，解决了复杂结构节点繁多问题。

c.传感器优化布置后，3种工况水闸底板脱空参数及脱空面积的反演精度均明显提高，脱空参数识别值相对误差的平均值分别从28.3%、15.8%、39.3%降低至1%、1.9%、15.9%，且脱空面积识别值的相对误差降低至4.5%，为水闸底板脱空测点布置提供了理论依据。