一种基于RCS测量的精度评定方法

张亚奇，鲁高飞，颜 元，田雨雷

(西安卫星测控中心，陕西 西安 710043)

0 引言

随着雷达测量技术的发展，雷达测量不仅希望得到被测目标的位置和速度等外弹道信息，还希望取得更多的目标特性，从而推导出目标的形状和体积等，达到目标识别的目的，雷达散射截面(Radar Cross Section,RCS)便是最重要、最基本的一个目标特性[1-3]。在雷达跟踪目标时，由于受内外部环境的影响，RCS测量数据中往往包含严重偏离目标真值的数据，这些严重偏离目标真值的数据就是所谓的“野值”。野值的特点是无规律、幅值大、持续时间短，因此在处理数据时，必须分离和剔除这些野值，提高处理结果的精度，从而准确反映目标的RCS值[4-7]。

RCS是雷达装备试验鉴定指标体系的重要组成部分[8]，本文提出了一种基于天基合作目标的RCS精度评定方法。利用天基合作目标来获取雷达测量数据，在数据处理过程中，利用莱特准则剔除野值，提高了计算精度和结果可靠性。

1 建立模型

1.1 坐标系及雷达视线角定义

地固坐标系定义为：坐标原点为地心，+X轴指向赤道面与本初子午线的交点，+Z轴指向地球北极，+Y轴与+X，+Z成右手系。

目标飞行轨道坐标系定义为：坐标原点为目标质心，+Y轴指向轨道面负法向，+Z轴指向地心方向，+X轴与+Y,+Z轴成右手系，大致指向目标速度方向。

目标质心坐标系定义为：坐标原点为目标质心，+Z轴方向为坐标原点指向龙伯球方向，-Y轴方向为坐标原点指向中间太阳翼法向，+X轴与+Y，+Z轴成右手系。质心坐标系定义图如图1所示，在质心坐标系中定义雷达视线方位角和俯仰角分别如下：

雷达视线方位角A0：雷达视线在XOY平面上的投影与OX轴的夹角，与OX轴重合时为0°，从上向下看顺时针方向为正。

雷达视线俯仰角E0：雷达视线与OZ轴的夹角，与OZ重合时为0°，与XOY平面重合时为90°。

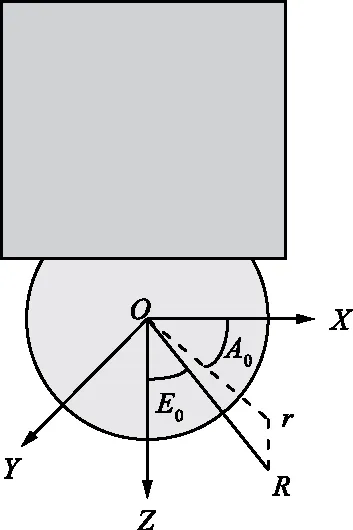
图1 目标质心坐标系定义Fig.1 Definition diagram of target centroid coordinate

1.2 坐标系转换

1.2.1 大地坐标系转换至地固坐标系

已知雷达在大地坐标系中的位置：经度为L，纬度为B，高度为h，则雷达在地固坐标系中的位置矢量为：

(1)

式中，N和e表示如下：

(2)

1.2.2 地固坐标系转换至目标轨道坐标系

计算得到雷达在地固坐标系中的位置矢量PR=[xR,yR,zR]T，根据该目标的星载GNSS接收机计算得到目标在地固坐标系下的位置矢量为PS=[xS,yS,zS]T，速度矢量为VS=[vSx,vSy,vSz]T。目标在地心惯性坐标系下的速度矢量为：

VSi=VS+ω×PS，

(3)

式中，ω=[0,0,ωe]T，ωe为地球自转角速率。

地固坐标系至目标轨道坐标系的转换矩阵[9]为：

Mfix2orb=[Vorbx,Vorby,Vorbz]T，

(4)

式中，

(5)

1.2.3 目标轨道坐标系转换至目标质心坐标系

目标的姿态角为：偏航角ψ，俯仰角θ和滚转角φ，则目标轨道坐标系至质心坐标系的转换矩阵为：

(6)

1.3 雷达微波入射角计算模型

雷达至目标的观测几何矢量为：

Vrad=PR-PS，

(7)

转换成单位矢量为：

(8)

将单位矢量从地固坐标系转换至目标质心坐标系，如下所示：

(9)

则雷达微波入射角为：

(10)

根据A0和E0，结合雷达工作频点和极化方式，在目标RCS基准数据库中，采用双线性插值算法，得到观测时段内的RCS基准值。

1.4 双线性插值算法

在实验室精确测量目标RCS值，测量范围为：入射角A覆盖0°～360°，入射角E覆盖0°～90°，A，E间隔均为1°，形成RCS基准数据库，数据库中的每一个RCS值都对应2个变量A和E，可以看成函数RCS(A，E)。双线性插值算法就是将含2个变量函数的线性插值进行扩展，其核心思想是利用与待插值RCS基准值临近的4个RCS值进行加权平均，得到待插值的RCS基准值。

已知雷达入射角A0和E0，待插值RCS(A0，E0)临近的4个RCS值为RCS(A1，E1)，RCS(A1，E2)，RCS(A2，E1)和RCS(A2，E2)，则双线性插值计算如下：

(11)

2 优化观测数据

由于空间环境的影响，雷达的距离、角度和RCS测量值常产生野值，严重影响RCS数据的处理和分析。根据莱特准则[10-11]，当观测数据服从正态分布时，残差落在3倍标准差[-3σ，3σ]范围内的概率超过99.7%，落在此区域外的概率不超过0.3%，因此，可以认为此区域外的测量数据为野值，需先剔除野值，优化观测数据。

RCS的计算公式[12-13]为：

(12)

式中，Pt为发射机输出功率；V为接收机输出电压；A为接收机总增益；R为目标距离；G为天线增益；f为雷达工作效率；c为光速；La为大气衰减；Lf为馈线总损失。

从式(1)可以看出，RCS值与雷达测距值有关[14-15]，且雷达观测情况与俯仰角有关，故首先剔除距离值和俯仰角的野值。测量误差为：

Ei=Oi-Ci，

(13)

式中，Oi为测量值；Ci为基准值；i为距离值或俯仰角。测量误差的算术平均值为：

(14)

根据莱特准则，标准差为：

(15)

以3σ为门限剔除Ei的野值，即当

(16)

Oi为野值，应予以剔除。将对应距离、俯仰角和RCS野值时段内的RCS值剔除，得到RCS优化值。

3 精度分析

RCS测量误差包括系统误差和随机误差[16-17]。系统误差是由一些已知原因所引起的并且可以设法消除或精确估计的误差，如测量设备的系统性偏差引起的误差。消除系统误差的途径主要有：消除产生系统误差的根源；在测量过程中采取措施，避免把系统误差引入测量结果；设法掌握系统误差的变化规律，建立数学模型，采用统计方法进行估计等。随机误差是由于在测量过程中一系列有关因素微小的随机波动而形成的误差，可以通过增加测量次数取平均值的办法减小随机误差。

对优化后的RCS值，计算系统误差和随机误差，并结合雷达的指标要求，分析评估RCS精度。RCS的误差为：

αi=10×(lgORCS-lgCRCS)，

(17)

式中，ORCS表示测量值；CRCS表示基准值。

系统误差为误差的算术平均值，即：

(18)

随机误差为：

(19)

4 实例验证

将该方法应用于某型雷达进行验证。

4.1 获取观测值和基准值

目标过境时，雷达实时跟踪目标，得到距离值、方位角、俯仰角及RCS测量数据。利用目标下传的星载GPS观测数据，处理得到观测时段的目标精密轨道，根据目标精密轨道和设备站址信息，计算得到观测时段内雷达微波入射角A0和E0。根据雷达的工作频点、极化方式、A0和E0，在目标RCS基准数据库中，采用双线性插值式(11)，得到观测时段内的RCS基准值。

4.2 优化观测数据

根据式(14)和式(15)计算测距误差的算术平均值为16.632 1 m，标准差为7.901 8 m，以3σ为门限剔除距离值Ri的野值，即当Ri>40.337 5 m或Ri<-7.073 3 m时，剔除Ri，得到如图2所示的误差曲线。

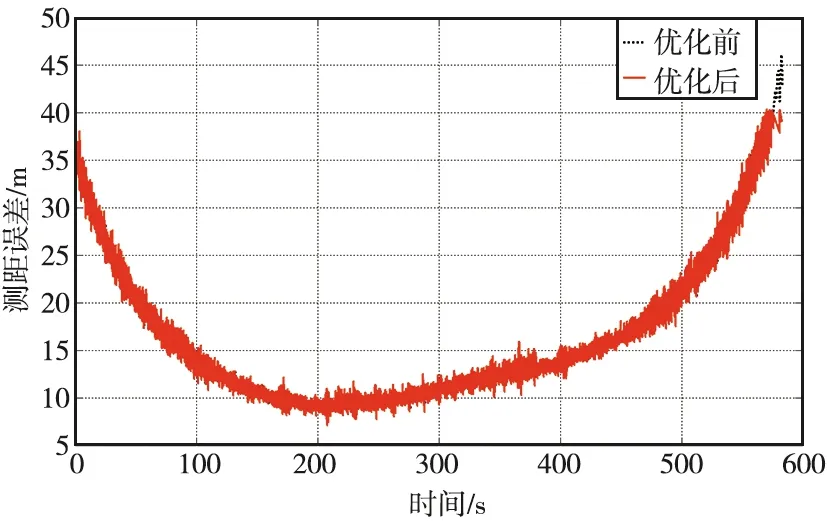
图2 测距误差优化前后对比曲线Fig.2 Comparison curve of ranging error before and after optimization

计算俯仰角误差的算术平均值为0.083 9 rad，标准差为0.060 2 rad，以3σ为门限剔除俯仰角Ei的野值，即当Ei>0.264 5 rad或Ei<-0.096 7 rad时，剔除Ei，得到如图3所示的误差曲线。

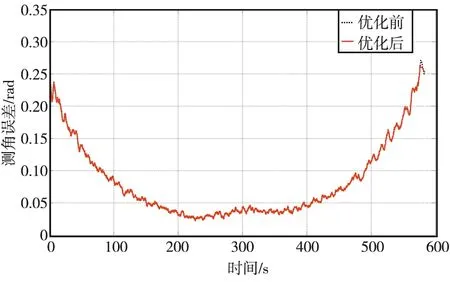
图3 测角误差优化前后对比曲线Fig.3 Comparison curve of angle measurement error before and after optimization

由图2和图3可以看出，距离值和俯仰角的野值主要为跟踪开始和结束的一小段观测数据，符合实际情况，即雷达在跟踪开始和结束时段内，天线俯仰角低，受大气折射和地面衍射等影响较大，容易产生测量野值。对剔除野值后的RCS值进行处理，计算其算术平均值为-1.432 4 dB，标准差为3.626 9 dB，以3σ为门限剔除野值，即当RCSi>9.448 3 dB或RCSi<-12.313 1 dB时，剔除RCSi，得到如图4所示的RCS误差曲线。

图4 RCS误差优化前后对比Fig.4 Comparison curve of RCS error before and after optimization

由图4可以看出，RCS野值主要出现在跟踪结束的一段时间内，剔除该部分野值后，对剩余RCS值进行计算系统差和随机差。

4.3 计算精度

采用式(18)和式(19)计算得到RCS的系统差为-1.432 4 dB，随机差为3.626 7 dB，该雷达系统差指标要求为<2 dB，计算结果满足指标要求。

将该方法应用于多套雷达进行跟踪验证，得到RCS精度计算结果如表1所示，计算结果均满足设备指标要求，证明了该方法的正确性。

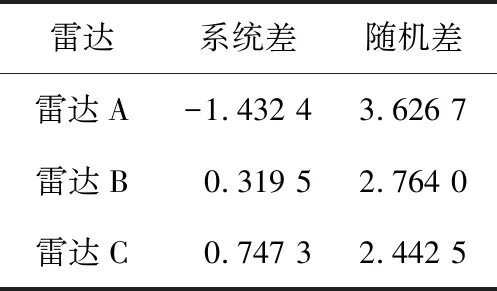
表1 RCS精度计算结果

5 结束语

本文研究了一种RCS精度评定方法，即利用天基合作目标精确的轨道数据和RCS值，采用野值剔除和双线性插值等方法，对RCS测量精度进行快速准确的评定，并将该方法应用于多套雷达的测量精度评定工作，计算结果符合雷达实际工作能力，验证了该方法的正确性和有效性。该方法有利于装备管理人员快速掌握并且提高雷达的测量精度，提高雷达装备工作的可靠性。

由于目前采用雷达单次观测数据进行处理得到系统误差和随机误差，可能受雷达内外部环境影响带来的偶然性因素，一定程度影响评定结果，因此，后续需要在雷达观测时长、观测次数和评定指标等方面进行研究，以尽可能减小偶然因素的影响，使评定结果能够最大程度反映雷达的工作能力。