基于Z向直线系统动态平衡结构仿真分析

崔海龙，乔 丽，曹国斌，丁宇心，郝艳鹏

(中国电子科技集团公司第二研究所，山西 太原 030024)

磁性材料作为重要的功能材料，广泛应用于自动化设备、计算机、电气仪表、机械加工等诸多方面，与自动化、信息化、国民经济等各方面息息相关。

磁性材料根据充磁后消磁的难易程度分为硬磁性材料和软磁性材料，在实际生活和工程应用中主要以硬磁性材料的永磁体为主。常见的硬磁性材料主要有钛钴合金、铝镍钴合金、钕镍硼和铁氧体等。

由于永磁体存在圆形、方形等多种形式，且充磁、实际工况对磁场和磁力影响都比较大，当前对永磁体的磁力计算主要依靠几种经验公式，且比较复杂，因此探索一套简便快捷且切实可行的计算方案至关重要。柴凯、杨庆超、朱石坚等人[1]通过等效磁荷法建立了磁极化强度和磁偶极子的关系，进而求导得到磁力；章跃进、江建中和屠关镇[2]采用数值解析结合法推导气隙磁场的表达式，用矢量磁位相等的条件得到解析方程；田录林、贾嵘、杨国清等人[3]基于电流镜像法及永磁体等效电流模型，计算了永磁铁贴合体的磁场和磁力；Muzitskii V F和Kudryavtsev D K[4]运用有限元法讨论了无损磁中磁体尺寸的关系，得到了相应的间隙距离公式。这些方法针对某一种特定工况进行了具体分析。

1 两相对强磁磁力理论计算

本文主要针对条形磁铁进行理论计算。条形磁铁主要有最大磁能积、磁感应强度、磁场强度和磁化强度等参数。最大磁能积代表了磁铁两磁极空间所建立的磁能量密度，即气隙单位体积的静磁能量，它是磁感应强度B和磁场强度H乘积的最大值，它的大小直接表明了磁体性能的高低。

磁感应强度B是指描述磁场强弱和方向的矢量，单位为特斯拉(T)。

磁场强度H是由磁荷观点引出的，类比于库伦定律，单位是A/m。

磁化强度M是描述宏观磁铁磁性强弱的物理量，定义为媒质微小体元ΔV内的全部分子磁矩矢量与ΔV之比，单位A/m。

其中，M、B和H之间主要有以下两种经验计算公式：

式(1)中，μ0为介质磁导率，空气中磁导率约等于真空磁导率，为4π×10-7H/m。

式(2)中，γ为介质的磁化率，顺磁质为正，抗磁质为负。

永磁铁的磁力计算较为复杂，主要依靠经验公式。对于强磁来说，能够吸起自身重力600倍的物品：

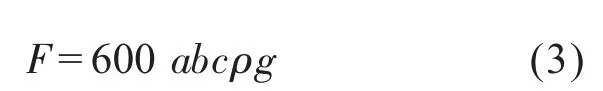
式(3)中，a、b、c、ρ、g分别为条形磁铁的长、宽、高、密度和重力加速度。

此外有部分理论计算，但并不完善，式(4)为单块磁铁零间隙吸力公式[5]：

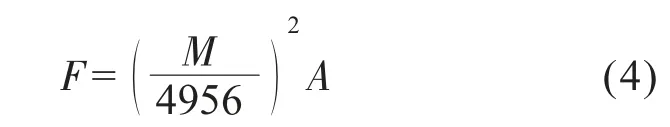
式(4)中，F为吸力；A为磁极面积，A=ab。联立式(3)和式(4)，可以得到：

本文所设计的磁铁尺寸a×b×c=116 mm×28 mm×5.6 mm，带入式(5)，可以得到M的值为2 462 A/m，M的值受磁铁厚度c值的影响。

考虑间隙和漏磁后，该公式变为：

式（6）中，α为修正系数，3～5，与间隙大小有关，间隙大取大值，间隙小取小值；L为磁铁之间的间隙，单位mm。

2 两相对强磁磁力仿真计算

采用WORKBENCH静磁学对两个相对的强磁进行仿真，图1所示为两磁铁网格划分示意图。

图1 磁铁网格划分示意图

本文仿真采用强磁的牌号为N45，N45磁铁所对应的剩磁约为1.35 T，矫顽力约为9×106A/m，据此设置仿真材料参数；选择两磁铁上下表面为充磁方向，确定两块磁铁的NS极，使得其N极和S极相对，能够相互吸引，设置求解方案，添加磁通平行方案后进行求解，得到其总磁通密度、总磁场强度和磁极法向合力等关键参数。

图2、图3所示为磁铁仿真得到的总磁场强度和磁极法向受力云图。从图(2)中可以看出，最大磁场强度主要出现在磁铁的表面，且由于是条形磁铁，呈现出规律性的平行磁感应线。磁极法向受力数值为负值，与图(3)中方向相反，符合两磁铁相吸的设置，表明充磁方案正确。

图2 总磁场强度

图3 磁极法向受力

通过设置WORKBENCH仿真参数集，改变两磁铁之间的间隙，可以得到不同的法向受力情况。此外，根据式（6）可以得到相应间隙磁铁的受力数值。为验证理论计算和仿真的正确性，使用了推拉力计和两块N45条形磁铁进行试验，如图4所示。

图4 试验测试实物图

得到的理论、试验和仿真结果如表1和图5所示。

表1 三种方法计算结果

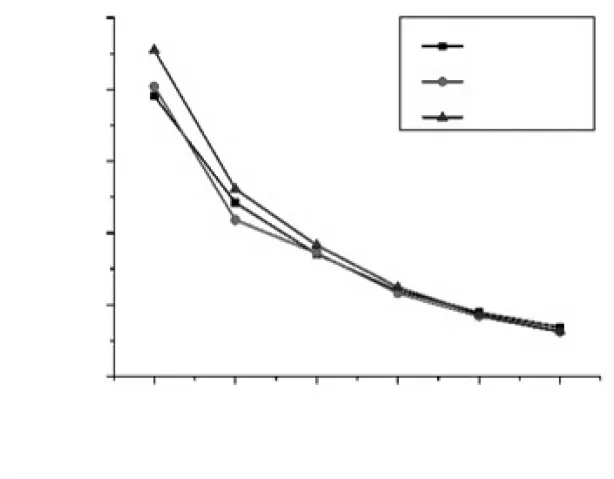
图5 三种方法计算结果折线图

从表1和图5中可以看出，仿真计算与理论计算和试验测试比较接近，误差在10%以内，表明仿真结果准确性比较高。分析三者存在误差的原因主要有以下两点：

图5 吸极电源实测图

（1）理论计算中M值是由经验公式所得到的，本身存在一定的误差；其次由于修正系数α随着间隙而变化，因此在计算中需要选择修正系数；

（2）试验测试中误差主要出现在N45强磁的材料属性与仿真所设置的材料属性并不是完全一致，存在些许误差。

综合来看，仿真结果的可信度很高，故该仿真参数设置及载荷约束添加方法是可行的，可以应用到自动贴片机中较为复杂的磁力仿真分析中。

3 磁铁芯-磁力座仿真分析

本文所设计的Z向直线系统动态平衡结构如图6所示，采用了磁铁芯-磁力座的结构，由于磁铁芯上带有负载，如果不能依靠永磁铁磁力带动磁铁芯上固定的负载复位，就会使得磁铁芯脱落，造成设备安全和生产问题。该结构采用了4块大小一致的条形磁铁，但是存在可以被磁化的顺磁性支座，且在直线运动过程中磁极相对的面积会改变，因此理论计算比较困难，在设计阶段采用仿真选择磁铁型号较为合适。

图6 Z向直线系统动态平衡结构

按照上述仿真参数设置进行仿真，得到总磁通密度仿真图及合力图如图7、图8所示。

图7 总磁通密度

图8 合力情况

从图7可以看出，磁铁芯拉到磁力座末端后，总磁通密度和总磁场强度均在磁铁芯和磁力座仅存的相对面达到最大值，从图8来看，最大的力也出现在该位置，且方向偏向磁力座另一端。

图9为磁铁芯竖直方向的受力情况图，磁铁芯所受到的竖直方向合力为73.6 N，而设计预估磁铁芯所带负载为4.5 kg，表明该结构和磁铁能带动负载复位。

图9 磁铁芯竖直方向受力情况

将磁铁芯和磁力座装到设备上进行实际测试，将磁铁芯缓慢拉到磁力座末端保持不动，通过测力计测得此时力为36.3 N，加上负载之后总的力为80.3 N，与仿真结果比较接近，相差在10%左右。

造成这种误差的原因有很多，主要集中在以下两个方面：

（1）磁铁本身存在差异。N45磁铁本身在生产过程中存在一定的误差，4块磁铁并不是完全一致，而仿真则是使用完全一致的磁铁，且实际磁铁磁极表面四周磁感应强度高于中心磁感应强度，而仿真则使用的是平均强度；

（2）安装存在误差。由于N45磁铁磁性较强，因此安装比较困难，在安装的过程中，很难保证两相对磁铁之间的间隙与所设计的一致，且所设计间隙本身较小，故很小的安装误差都能够引起较大的结果偏差。

4 结束语

（1）通过理论计算和试验测试，验证了磁力仿真中参数设置和流程方案的可行性，磁力仿真结果具有较高的可信度，该流程能够在Z向直线运动动态平衡结构中使用。

（2）通过仿真和试验发现，本文所选用的磁铁及设计的Z向直线系统动态平衡结构能够有效带动负载复位，避免了负载脱落与其他部件发生碰撞，同时验证了磁力仿真的正确性，为复杂磁力工况设计计算提供了仿真支持。