基于IFDO-LSSVM的空气质量指数预测
胡进才, 张 菁, 王大龙, 吕 伟, 欧阳文安
(上海工程技术大学 电子电气工程学院,上海 201620)
0 引 言
雾霾天气的出现对身体健康、农作物生长以及国家长远发展都有严重影响[1]。因此,监测空气质量十分有必要。根据国家的规定,一般选取NO2,O3,CO,PM 2.5,PM 10,SO2六项检测指标,再用空气质量指数(air quality index,AQI)直观地反映空气质量[2,3]。
在对AQI预测模型中,最小二乘支持向量机(least square support vector machine,LSSVM)模型应用最为广泛,但LSSVM不能准确选择参数。对此,文献[4]选择在每次迭代中全部个体的均方误差的最小值作为适应度函数,再利用粒子群优化(particle swarm optimization,PSO)算法对LSSVM的两个参数优化,从而能够精准预测;文献[5]通过鲸鱼优化算法(whale optimization algorithm,WOA)对LSSVM模型的两个参数优化,得到锅炉NOx排放量的预测模型;文献[6]通过樽海鞘群优化算法(SSA)进行寻优,再通过K均值聚类和SSA-LSSVM共同建立预测模型,对短期负荷进行预测;文献[7]通过利用自适应位置更新和高斯变异来对灰狼优化(GWO)算法进行改进,然后优化LSSVM的参数,最终能够对磨矿粒度进行预测;文献[8]通过利用非线性惯性权重来改进萤火虫算法(FA),再把改进的算法用来优化LSSVM的参数,最终实现对粮食产量的预测。
上述文献中,虽然各模型都能实现预测,但精度不高,并且优化算法中初始群体是随机产生的,容易扩大寻优范围使迭代次数增加,不利于寻找最优解。为解决上述问题,本文提出一种基于改进的适应度相关优化器(improved fitness dependent optimizer LSSVM,IFDO-LSSVM)的预测方法。
1 LSSVM
LSSVM[9,10]是一种机器学习方法[11]。其具体内容如下:
在给定的数据训练集{(xi,yi)|i=1,2,…,m},其中,m为训练样本数,LSSVM的优化模型可以表示为
(1)
s.t.yi=wTφ(xi)+b+ei,i=1,2,…,m
(2)
式中w为权重,C为惩罚参数,ei为松弛变量,b为误差;φ(xi)为一种映射关系。
利用Lagrange法求式(1)、式(2)的优化问题,构造成函数为
L(w,b,e,α)=J(w,b,e)-
(3)
式中α为Lagrange乘子,即α=[α1,α2,…,αm],并且每个元素都大于零。
再利用KKT条件,对式(3)中w,b,ei,αi求偏导,得
(4)
(5)
(6)
(7)
然后根据式(4)消除式(7)中的w,用式(6)消除式(7)中的ei,可以把式(5)、式(7)最终整理为
(8)
其中,i=1,2,…,m;j=1,2,…,m;令:K(xi,xj)=φ(xi)Tφ(xj),其中K(xi,xj)代表核函数。然后对式(8)进行求解,可得LSSVM的回归方程
(9)
由于径向基函数结构简单,参数少[12],因此,选择径向基函数作为核函数,即表示为
(10)
式中σ为核函数的参数。
2 适应度相关优化器
2.1 适应度相关优化器算法
适应度相关优化器(fitness dependent optimizer,FDO)算法[13]是由Abdullah J M和Rashid T A在2019年提出的一种新启发式算法。算法通过蜜蜂在繁殖时的行为和蜂群决策而受到启发。在这个过程中主要包括两个阶段,即是搜索过程和移动过程。
算法中,先设置迭代次数max_iteration、群体数目u、优化问题的维数v、优化对象的范围、初始群体的位置、初始速度的大小、适应度函数。其中,初始群体为
X(u,v)=(g(1,v)-h(1,v))×
rand(u,v)+h(1,v)
(11)
式中g(1,v)为优化对象最大值;h(1,v)为优化对象最小值;v为优化对象维数;u为群体数目;u,v取正整数。
搜索过程:通过式(11)在规定范围内产生初始蜂群(侦查蜜蜂数目),每个侦查蜜蜂的位置代表一个解。每个侦查蜜蜂通过随机机制搜索更多蜂巢(解),每发现一个更好的解,先前的解将被忽略。如果目前搜索的解没有先前效果好,则下次搜索方向将按照先前方向搜索,但搜索出的解还是没有先前效果好,则下次搜索将继续使用先前的解。
移动过程:每个侦查蜜蜂通过增加速度来更新此时的位置,以此得到更好的解。侦查蜜蜂移动位置的更新公式如下
Xi,t+1=Xi,t+pace
(12)
式中i为当前群体中第i个侦查蜜蜂;t为当前第t次迭代;X为每个侦查蜜蜂的位置;pace为侦查蜜蜂移动的速度和方向;pace主要由适应度权重wf决定,pace的方向只有随机机制决定。适应度权重wf的计算公式如下
(13)
(14)
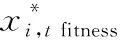
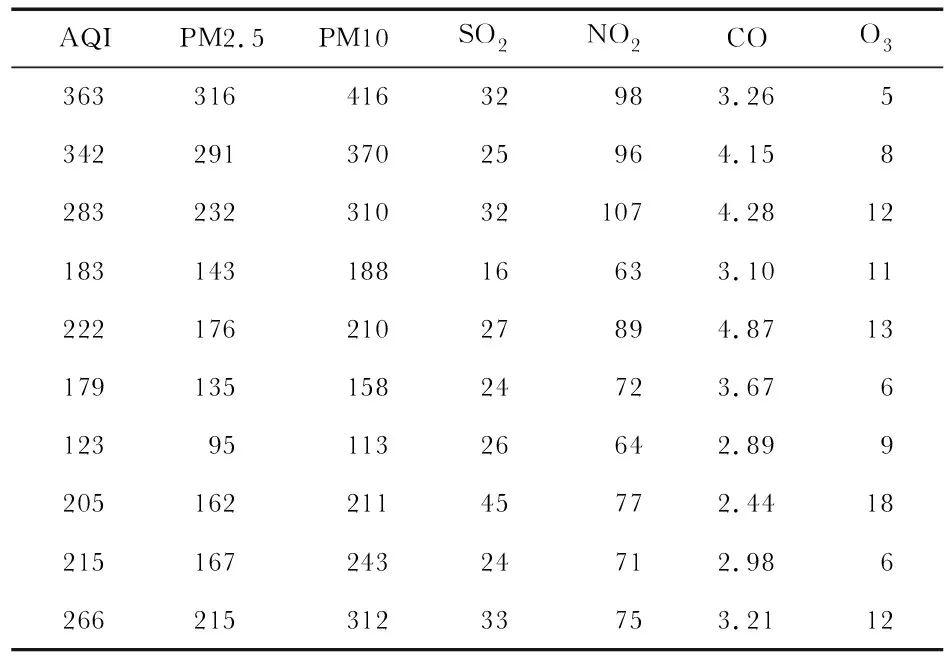
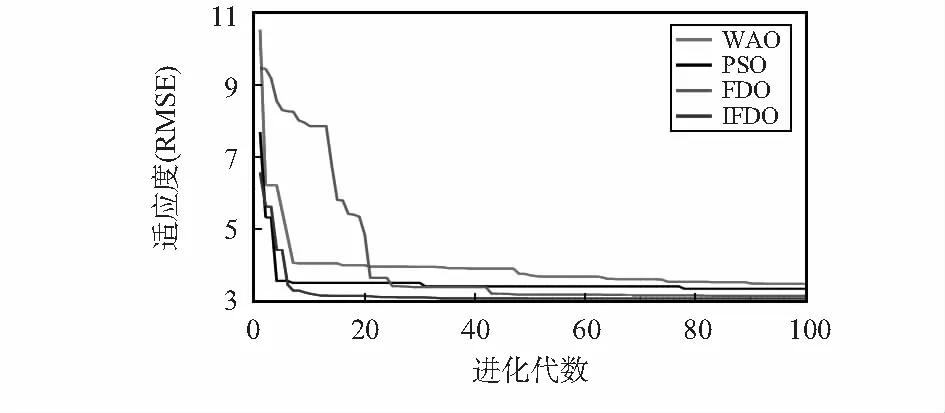
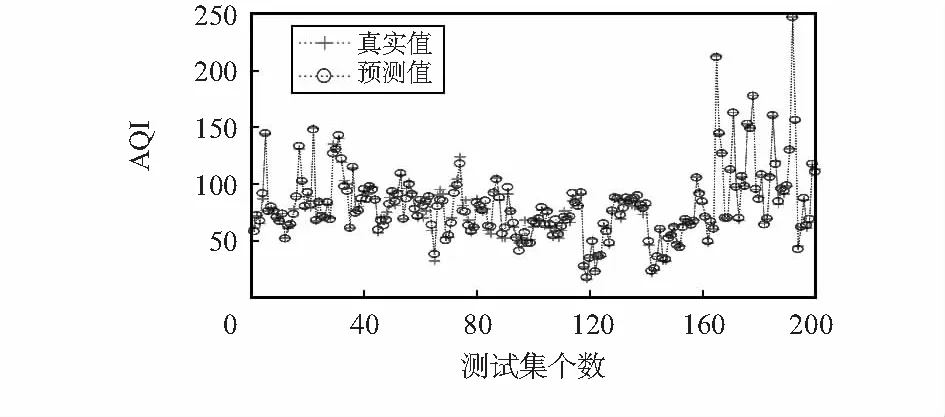
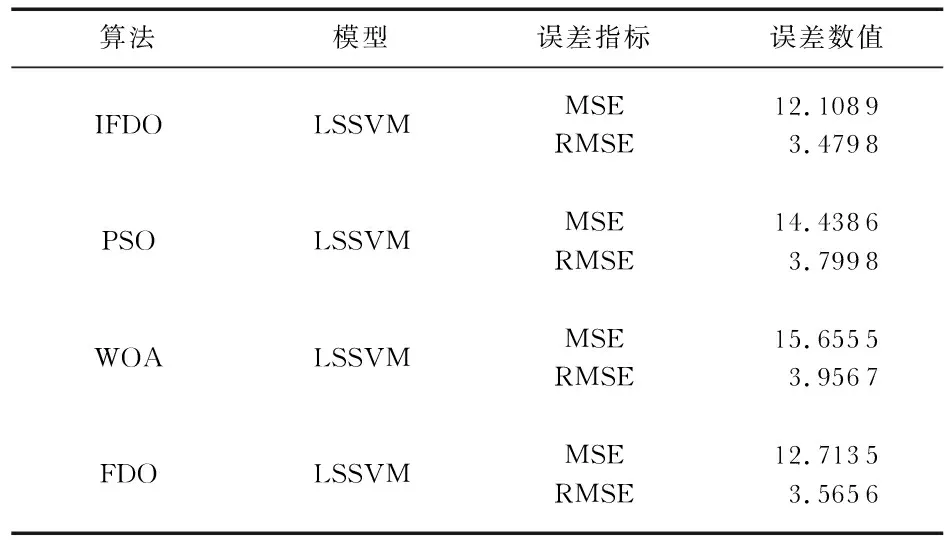
再由wf得到速度的值,r属于[-1,1]中的随机数。当wf=1,wf=0,xi,t fitness=0时,执行式(15);当0 wf=1 orwf=0 orxi,t fitness=0⟹pace=xi,t*r (15) (16) (17) X1(2u,v)=(g(1,v)-h(1,v))×rand(2u,v)+ h(1,v) (18) 基于IFDO-LSSVM的预测模型步骤如下: 步骤1 利用Mapminmax函数对数据进行预处理。 步骤2 设置FDO算法的参数:迭代次数max_iteration,群体数目u,优化问题的维数v,优化对象的范围g(1,v)和h(1,v),初始速度pace,适应度权重系数αw=1。 步骤3 选择合适的适应度函数,在此处选择数据的标准误差均方根误差(root mean square error,RMSE)作为适应度函数,公式如下 (19) 式中m为训练数据的个数;X″i为预测值,Xi为真实值。 步骤4 利用2.1节的方法产生初始群体,同时用式(19)得到适应度函数值。 步骤5 当t≤max_iteration时,更新wf,pace,X。 步骤7 更新r,然后当wf=1,wf=0,xi,t fitness=0时,执行式(15);当0 步骤8 如果通过步骤7更新xi,t fitness比之前效果好,那么保存pace,xi,t fitness和X;否则,利用之前X的和步骤7中的pace,通过式(20)更新X,利用式(19)更新xi,t fitness Xi,t+1=Xi,t+pace+pace* (20) 式中pace*为在第t-1次迭代时第i个位置对应的速度。 步骤9 如果通过步骤8更新xi,t fitness比之前效果好,那么保存pace,xi,t fitness和X;否则,在步骤8中X的基础上随机生成X,同时利用式(19)更新xi,t fitness。 步骤10 如果通过步骤9更新xi,t fitness比之前效果好,那么保存xi,t fitness和X;否则,X为本次迭代开始的X。 步骤11 执行t=t+1,循环步骤5~步骤10,当t大于 max_iteration时循环结束。输出u个X,在u个X中找到全局最优解x*。 步骤12 步骤11中的x*为LSSVM中的两个参数C和σ。将C和σ以及预测数据代入到LSSVM模型中,即可得到预测结果。 实验中,通过天气后报数据网站(http:∥www.tianqihoubao.com/)收集郑州市在2017年~2019年750组天气数据,如表1所示。 表1 部分实验数据 其中,550组数据为训练样本,200组数据为测试样本,AQI为预测对象。NO2,O3,CO,PM 2.5,PM 10,SO2这6个指标作为输入对象,建立模型。由于6个指标量纲不同,对预测结果会产生影响。因此,用Mapminmax函数对数据预处理,得到的数据在区间[0,1]中,公式如下 (21) 式中ymax为指定预处理所到区间的最大值,ymin为指定预处理所到区间的最小值,x为样本数据,x′为处理后的数据,xmax,xmin分别为样本的最大值、最小值。 在Windows10操作系统中,利用MATLAB R2016b软件进行实验。对FDO算法设置参数:max_iteration为100,u为50,v为2,C取值范围为[0.1,500],σ取值范围为[0.1,100],对于此外的PSO算法、WOA中参数设置与FDO算法相同。选用式(19)作为适应度函数,式(19)、式(22)作为评价指标 (22) 用IFDO算法、FDO算法、PSO算法、WOA进行寻优,四种算法的适应度变化曲线对比图,如图1所示。 图1 适应度曲线对比 从图1可以看出,FDO算法、WOA、PSO算法和IFDO算法在寻优时适应度的起始点所在范围分别为[9,10],[10,11],[7,8],[6,7]。FDO算法、WOA和PSO算法随机产生初始群体,而IFDO算法利用改进的反向学习算法产生初始群体。因此,从图中可以看出,IFDO算法的收敛精度更高,初始群体更加靠近全局最优解,从而寻优范围变小,便于寻优。用IFDO算法寻优时在30~40代之间收敛,用FDO算法寻优时在40~50代之间收敛,用PSO算法寻优时在70~80代收敛,用WOA寻优时在80~90代收敛,因此,IFDO算法比FDO算法、PSO算法和WOA收敛快。 在通过上述算法寻优后,取得最优参数C和σ。用IFDO算法优化参数为C=496.031 7,σ=0.100 1,预测结果如图2所示。 图2 AQI的真实值与预测值 四种模型的预测精度如表2所示。 表2 四种算法预测误差的对比 选择MSE和RMSE作为评价指标,这两个指标越小,说明预测精度越高,预测误差越小。从表2中可以看出,通过WOA-LSSVM得到MSE和RMSE分别为15.655 5,3.956 7;通过PSO-LSSVM得到MSE和RMSE分别为14.438 6,3.799 8;通过FDO-LSSVM模型得到MSE和RMSE分别为12.713 5,3.565 6;通过IFDO-LSSVM得到的MSE和RMSE分别为12.108 9,3.479 8。因此,在四种模型中,IFDO-LSSVM的模型具有最高精度,最小误差。 1)本文提出一种基于IFDO-LSSVM的AQI预测模型,模型中,IFDO算法收敛速度快,初始群体更靠近全局最优解,从而有利于搜索全局最优解。 2)通过三种模型对AQI预测发现IFDO-LSSVM预测模型精度最高,误差最小。因此,该方法对AQI能够实现有效预测。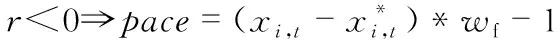
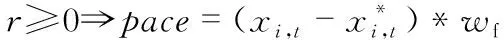
2.2 基于IFDO-LSSVM的预测模型

3 实例分析
3.1 数据的来源与预处理
3.2 实验参数的设置和结果分析
4 结束语

