无缝钢管涡流检测速度效应仿真研究

赵学永， 周德强

(江南大学 机械工程学院，江苏 无锡 214122)

0 引 言

为了确保无缝钢管的出厂质量，20世纪80年代国内的一些无缝钢管生产企业就开始使用涡流与超声波自动探伤设备对成品钢管进行出厂检验。经过几十年的发展，无缝钢管的产品质量逐步提高，自动探伤设备的检测能力也迅速发展[1]。目前可应用于检测运动中无缝钢管缺陷的无损检测方法[2～4]使用中存在各自的不足。其中，超声波检测法需要介质进行耦合，这不仅限制了在实际生产过程中的检测速度而且对检测环境的要求较高；在高速检测中应用漏磁检测法时，会产生强烈的磁滞效应，这不利于对检测信号的提取[5]；而射线检测由于检测设备较为复杂，不适合对运动的物体进行检测。涡流检测法是一种广泛应用于检测钢管的内外表面裂纹以及腐蚀缺陷的检测方法，目前国内外学者对钢管动态涡流检测已开展了一些研究。冯搏等人[6]对涡流引起的钢棒磁化滞后时间进行了研究；宋凯等人[7,8]研究了钢管的通孔直径对涡流检测特征信号的影响，分析了不同磁化程度下钢管的磁特性对涡流检测效果的影响；Wang P等人[9]研究了铁磁性钢管的磁导率以及磁化程度与磁化时间的变化关系；Nestleroth J B等人[10]对用永磁体运动产生的涡流对管道异常和壁厚变化进行了检测，但是针对在不同检测速度下，钢管内部涡流场、磁场的分布情况以及钢管外壁缺陷信号表征方法的研究相对较少。

本文首先对无缝钢管涡流检测时速度效应机理进行了分析，然后建立了有限元仿真模型，结果表明：当待测钢管与激励线圈之间存在相对运动时，钢管内部产生了动生涡流(motion induced eddy current,MIEC)，同时由激励线圈激发的磁场强度也有显著的变化；可以通过磁通密度的峰值对钢管外壁环形缺陷的宽度及深度进行表征。

1 涡流检测速度效应机理分析

在钢管涡流检测的过程中，激励线圈用来产生一个恒定的磁场，根据法拉第电磁感应定律，由于激励线圈与钢管之间的相对运动，钢管内部会产生MIEC[11]。当钢管的表面存在缺陷时，MIEC就会受到缺陷的扰动，由MIEC激发的磁场也会由于缺陷的存在而改变。在进行涡流检测时，钢管中的MIEC强度可以描述为

Jm=συ×B

(1)

式中Jm为MIEC的强度；σ为钢管的电导率；υ为探头与钢管的相对运动速度；B为由激励线圈激发的磁场强度。

假设由激励线圈激发的磁场强度保持不变，那么描述探头与试件之间相对运动的麦克斯韦公式的微分形式可以表示为

(2)

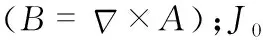
(3)

将由加载正弦激励的激励线圈激发的恒定磁场强度定义为B。当运动中的待测钢管靠近激励线圈时，由于相对运动的作用，将会在钢管内部激励线圈的两侧产生MIEC，定义为J1，J2。同时，将由MIEC产生的磁通密度定义为B1，B2。由于恒定磁场B的作用，钢管本身也会被磁化，因此会产生与恒定磁场同方向的磁通密度，定义为B3。MIECJ1，J2与磁通密度B,B1，B2，B3的分布如图1所示。

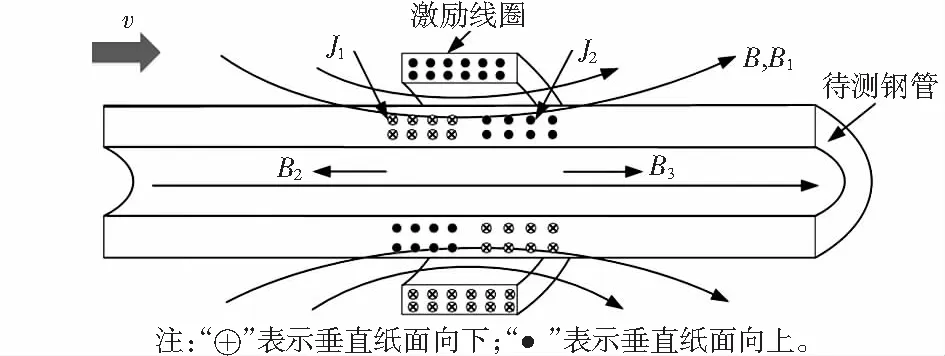
图1 MIEC和磁通密度在运动钢管中的分布

由图1可知，在激励线圈的两侧产生了方向不同的MIEC，与此对应的产生了方向不同的磁通量。在激励线圈的左侧，MIEC产生的磁通量与激励线圈产生的磁场方向大致相反，在激励线圈的右侧，MIEC产生的磁通量与激励线圈产生的磁场方向大致相同。即在激励线圈左侧时，MIEC减弱了钢管的磁化程度，不利于涡流检测信号的提取。而在激励线圈的右侧时，MIEC增强了钢管的磁化程度，有利于涡流信号的提取。通过式(3)可以得出，对处于运动状态的钢管进行涡流检测时，合磁通量B′为

B′=B+B1+B2+B3

(4)

由以上分析可知，当钢管表面存在缺陷时，B′的值将会改变。因此，通过对磁通密度B′的大小进行测量，可以实现对钢管中缺陷的有效检测。

2 有限元仿真模型建立

如图2(a)所示，在Ansys Maxwell中建立了瞬态磁场状态下的三维仿真模型。为更好地说明三维模型，建立了如图2(b)所示的二维剖面图。如图2(b)所示，因为待测钢管与激励线圈之间存在相对运动，因此建立了图示运动域。在运动域中，可以给待测钢管指定运动速度。线圈处于静止状态，待测钢管沿着竖直方向向上运动。在图示检测点处对待测钢管上指定区域的磁通量进行检测。

图2 仿真模型

在建立的仿真模型中，提离高度为17.5 mm，采用电流激励方式，激励电流大小为0.1 A，激励频率为20 Hz。线圈以及待测钢管的几何参数以及物理性质如表1所示。

表1 几何参数

3 仿真结果与分析

3.1 速度效应对磁场与涡流分布的影响

基于本文建立的三维有限元仿真模型，探究速度效应对磁通量的影响情况。建立的缺陷模型中，缺陷高度0.5 mm，深度2 mm,长度10 mm。

图3所示,待测钢管与激励线圈的相对运动速度分别为0.1，0.5，1.0，2.0，5.0，10.0 m/s时，外壁缺陷运动至激励线圈中心位置时，钢管内部的磁场分布情况。可以得出，随着相对运动速度的增大，磁场强度逐步变大。由式(1)可以得出，当相对运动速度一定时，MIEC的大小与磁场强度成正比，因此进一步研究不同速度时MIEC的变化情况。

图3 不同检测速度时磁场云图

图4为不同检测速度时钢管内部涡流分布云图。由图4可以看出，受集肤效应的影响，由相对运动产生的MIEC主要集中在待测钢管的外壁。从前文的理论分析可知，待测钢管与激励线圈的相对运动速度越大，则MIEC的强度也随之变大。

图4 不同检测速度时涡流分布云图

可以清晰地看出涡流强度随着速度的增大而增大，并且也可以看出相对运动速度对待测钢管内部缺陷位置处MIEC场明显的拖拽效应。

3.2 磁通密度与钢管缺陷深度的关系

在图2所示三维仿真模型中，距离钢管上表面20 mm处建立了环形缺陷，缺陷宽度0.5 mm，长度10 mm,深度分别为壁厚的20 %，40 %,60 %,80 %。在图5(a)中，激励线圈与待测钢管的相对运动速度为0.1 m/s，图5(b)中，激励线圈与待测钢管的相对运动速度为1.0 m/s。

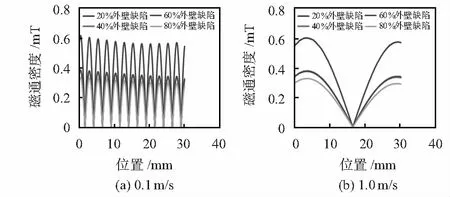
图5 不同速度时缺陷深度磁场强度信号

设置的检测区域为钢管上表面至30 mm处，图5表示检测区域以不同的速度经过在激励线圈中心位置的测量点时磁通密度的变化情况。图5显示,随着外壁缺陷深度的增大，磁通密度的峰值整体上呈现单调下降的趋势。图6显示,不同检测速度时，缺陷深度与磁通密度峰值的关系。

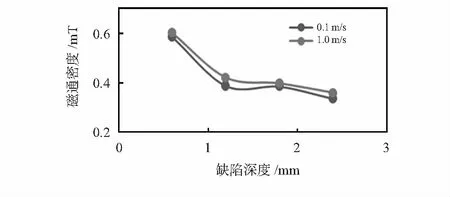
图6 不同检测速度时缺陷深度与磁通密度峰值关系

图6显示,当缺陷深度变大时，磁通密度峰值逐渐减小，且同一缺陷深度时，检测速度较大，磁通密度峰值较大。这是因为在进行管道检测时，由涡流效应引起的磁场在管道的外壁与激励线圈产生的磁场方向相反，这使得部分磁场相互抵消，又由于集肤效应的影响，涡流主要集中在外表面处，则表面处的磁场强度较大。因此，在进行外壁缺陷的检测时，深度较小的缺陷反而磁通密度的峰值越大，深度较大的缺陷磁通密度的峰值越小。

3.3 磁通密度与钢管缺陷宽度的关系

在图2所示三维仿真模型中，距离钢管上表面20 mm处建立了环形缺陷。缺陷深度1.5 mm，长度10 mm，宽度分别为0.5,1.0,1.5,2.0 mm。在图7(a)中，激励线圈与待测钢管的相对运动速度为0.1 m/s，图7(b)中，激励线圈与待测钢管的相对运动速度为1.0 m/s。

设置的检测区域为钢管上表面至30 mm处，图7表示测量区域以不同的速度经过在激励线圈中心位置的测量点时磁通密度的变化情况。

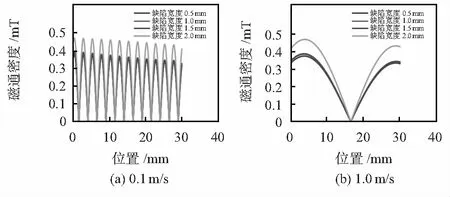
图7 不同速度时缺陷宽度磁场强度信号

图8显示随着外壁缺陷宽度的增大，磁通密度的峰值整体上呈现单调上升的趋势，且同一缺陷宽度时，检测速度较大，磁通密度峰值较大。与图7(a)相比，图7(b)显示当速度变大时，不同外壁缺陷深度的磁通密度峰值逐渐减小。这是因为集肤效应的影响，所以由于相对运动产生的涡流主要集中在钢管的外表面处，而且在运动过程中，其所受的磁场主要为激励线圈产生的径向磁场。随着外壁缺陷宽度的增大，缺陷位置处穿过磁场的缺陷面积逐渐增大，所以磁通密度的峰值越来越大。

图8 不同检测速度时缺陷宽度与磁通密度峰值关系

4 结 论

本文基于Ansys Maxwell建立了有限元仿真模型，研究了对无缝钢管进行涡流检测时，速度效应对钢管外壁缺陷宽度以及深度缺陷信号的影响，结果表明：

1)在对无缝钢管进行涡流检测时，由于待测钢管与激励线圈之间存在相对运动，在钢管内部产生了MIEC，且由理论分析可知，MIEC在激励线圈左侧时减弱涡流检测信号，在激励线圈右侧时增强涡流检测信号。随着相对运动速度的提高，MIEC的强度逐渐变大，且向缺陷位置集中；

2)随着待测钢管与激励线圈之间的相对速度逐渐增大，待测钢管内磁场强度显著增大；

3)无缝钢管外壁环形缺陷的深度以及宽度可以通过磁通密度的峰值进行表征。当外壁缺陷深度逐渐增大时，磁通密度的峰值逐渐下降；当外壁缺陷宽度逐渐增大时，磁通密度的峰值逐渐上升。