隐私保护众包软件测试激励机制设计
王 强,陈世航,徐 佳
(1.中国赛宝实验室,广州 广东 511370;2. 南京邮电大学 江苏省大数据安全与智能处理重点实验室,江苏 南京 210023)
软件测试借助大量的测试用例对软件产品进行全方位的测试,并基于反馈的测试结果,修复软件产品中的缺陷,改进产品的质量[1]。专业测试人员招募以及模拟测试环境构建显著增加了软件测试的成本。为解决这一问题,研究者提出了基于众包[2]的软件测试模式。众包软件测试能够通过众包的方式以较低的成本招募到合适的测试人员,同时保证软件测试环境为真实场景,可有效缩短软件测试周期和降低软件测试成本。
众包软件测试由3方组成:测试任务发布者、众包工人和众包平台,后文分别简化为发布者,工人和平台。软件测试任务需要根据任务大小、测试需求、设备需求、测试报告的规范等进行分类。工人需要具备基本的测试能力并配备相应的测试设备,同时了解测试的对象产品。众包软件测试通常通过拍卖的方式进行。发布者提交测试任务到平台,工人根据自身的资源提交想要执行的测试任务报价到平台。当平台收到工人提交的报价后,平台根据测试任务的需求,为不同类型的任务招募足够的工人,以完成测试任务。当工人完成任务后,将生成的测试报告提交到平台,平台将测试报告发送给发布者审核,审核通过的工人可以获得相应的报酬。
目前已经有部分研究者研究众包软件测试人员的招募问题[3],包括招募工人完成体验质量(Quality of experience,QoE)测试[4]、图形用户界面(Graphical user interface,GUI)测试[5]等功能性测试,以及测试用例生成[6]、程序调试与修复[7]等非功能性测试。同时也有部分工作研究工人之间的竞争[8,9]和合作[10,11]问题。另外,工人完成任务后提交的测试报告审核也是一项具有挑战的任务。文献[12]提出了使用多样性策略和动态风险策略对测试报告进行审核。文献[13]利用空间金字塔的方法比较测试报告的差异距离以审核报告的可用性。除此之外,众包软件测试框架设计也是目前主流的研究之一[14,15]。隐私安全也是众包软件测试中被重点关注的领域。Wang等[16]研究了工人的代码和身份隐私安全问题。文献[17]和[18]研究了数据库中心应用中的工人数据安全问题。上述工作均没有考虑众包工人的报价隐私保护问题。
由于参与测试任务的工人通常为理性且好奇的,他们都想要获得更多的收益并且企图获取其他工人的信息,所以可能存在以下两种攻击:(1)激励攻击:测试成本作为工人的隐私信息,攻击者在报价时通过上报一个不同于测试成本的报价来隐瞒自身的测试成本,而不诚实的报价可能会使攻击者能够获取更多的效用。因此,需要设计一个具有真实性的机制保证工人能够诚实地上报自己的测试成本;(2)推断攻击:为了保证公平性,平台会将获胜工人公布,那么攻击者能够通过公布的结果推断出其他工人的报价,这种攻击被称为推断攻击[19]。如果机制是真实的,工人会诚实上报自己的测试成本,那么推断攻击会导致工人的测试成本隐私暴露。因此,需要设计一个隐私保护机制保护工人的测试成本。
本文结合拍卖机制[20,21]以及差分隐私机制[22],设计了一个隐私保护众包软件测试激励机制。拍卖机制已在众包领域被广泛使用[23,24]。差分隐私机制能够保证对于任意一个工人报价的改变,输出的改变在可以控制的范围内,使得攻击者无法通过输出推断出工人的测试成本隐私[25]。本文以最小化招募工人的成本为目标,将问题建模为一个买家(平台)和多个卖家(工人)的反向拍卖模型,通过拍卖机制激励工人诚实的上报自己的成本,从而防止激励攻击。采用差分隐私中的指数机制[26]以概率选择获胜工人,实现工人的测试成本隐私保护。
1 系统模型和问题定义
1.1 系统模型
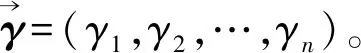
(1)
1.2 攻击模型
(1)激励攻击:众包软件测试系统中,工人是自私且理性的,所以工人有动机通过提交一个不同于测试成本的报价来提升自身的效用。
(2)推断攻击:真实的基于拍卖的激励机制会激励工人上报其真实的测试成本,即bi=ci。然而当工人上报其真实的测试成本时,其他的工人可能通过机制的输出(即获胜者)推断出这个工人的真实测试成本。
1.3 预期的性质
(1)计算有效性:如果一个机制能够在多项式时间内得到结果,那么此机制是计算有效的。
(2)个体理性:如果一个机制能够保证所有工人在诚实上报他的测试成本的情况下,所获得的效用是非负的,即ui≥0,那么此机制是满足个体理性的。
(3)真实性:如果一个机制能够保证工人在真实上报测试成本的情况下的效用是最大的,那么该机制是真实的。
除此之外,还需要保护工人的测试成本隐私,本文使用差分隐私机制保护工人的隐私安全。在此之前,先介绍差分隐私的定义。
定义1差分隐私[25]:一个随机机制M:Xn→Y能够提供 (ε,δ)差分隐私保护,当且仅当对于任意相邻数据集D,D′ ∈Xn(D和D′ 仅有一条记录不同),对于任意的输出O⊆Y,有
Pr[M(D)∈O]≤exp(ε)×Pr[M(D′)∈O]+δ
(2)
特别地,当δ=0时,机制M满足ε-差分隐私保护。

(1)Pri(z)关于bi是单调非递增的。
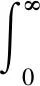
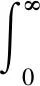
指数机制是差分隐私保护中常常使用到的机制。指数机制的关键是设计得分函数S(D,o),其中D表示输入集合,o∈O表示输出。得分函数是评估此输入和输出的分值,表示对于输入D来说,输出o相比于最优输出的好坏程度。

(3)
定义Λ为两个输入集合的差值的上界,那么就有以下定理。
定理2[24]指数机制满足2εΛ-差分隐私。
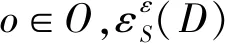
(4)
1.4 问题定义
本文的目标是在保护工人的报价隐私的情况下,最小化总测试成本,并且满足计算有效性、个体理性、真实性和差分隐私性。此测试成本最小化问题可形式化如下
(5)
s.t. ∪wi∈UTi=R
(6)
这个问题表示在保证所选择的工人能够完成所有测试任务的情况下,最小化总测试成本。
2 隐私保护众包软件测试激励机制设计
首先分析测试成本最小化问题的难度。
定理4测试成本最小化问题是NP-难的。
证明首先证明最小权重集合覆盖问题与测试成本最小化问题是等价的。
最小权重集合覆盖问题的实例:给定全集K和集合S={s1,s2,…,sn},任意si∈S是K的子集,即si⊆K。每个si的权重为w(si),问题是找到一个总权重最小的子集S′⊆S,并且S′中的元素能够覆盖全集K。
测试成本最小化问题的实例:给定测试任务集R和工人的任务集合T={T1,T2,…,Tn},任意Ti∈T是R的子集,即Ti⊆R。每个Ti对应的成本为ci,问题是找到一个总成本最小的子集T′⊆T,并且T′中所包含的任务能够覆盖测试任务集R。
综上所述,最小权重集合覆盖问题和测试成本最小化问题是等价的。最小权重集合覆盖问题是典型的NP-难问题,因此测试成本最小化问题也是NP-难问题。
本文提出的隐私保护众包软件测试激励机制如算法1所述。算法共包含3个阶段:工人筛选阶段,获胜者选择阶段以及报酬计算阶段。首先初始化已完成任务集合RU为空集,初始化候选工人集合Re为工人集合W(行1)。

算法1隐私保护众包软件测试激励机制



2:foreachwi∈Wdopi=0;
3:whileRU≠Rdo
//工人筛选阶段
4: foreachwi∈Redo
5: ifTi⊆RUthenRe←Rewi};
6: end
//获胜者选择阶段
7: foreachwi∈Redo
8: 基于式(9)计算每个工人被选中的概率Pri(bi);
9: end
10: 基于式(9)计算得到的概率分布,随机选择一个工人作为获胜者,记为w′i;
11:U←U∪{w′i};RU←RU∪Ti′;Re←Rew′i};
12:end
//报酬计算阶段
13:foreachwi∈Udo

15:end
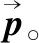

(1)工人筛选阶段。
算法4~6行,遍历候选工人集合,查看被遍历的工人的任务子集是否已经在已完成任务集合RU中。如果已经被RU所覆盖,那么就将这个工人从候选工人集合Re中删除。
(2)胜者选择阶段。
算法7~12行,为每一个在候选工人集合Re中的工人计算被选中的概率(行8),并根据概率分布随机选择一个工人作为获胜者(行10)。工人被选中的概率根据得分函数计算得到。在计算得分函数之前,首先确定每个工人wi的选择标准r(βi)
(7)
本文的机制是选择r(βi)最小的工人。下一步为选择标准r(βi)设计一个单调非递增的得分函数。本文将对数函数S(x)=log1/2x作为选择标准r(βi)的得分函数。对任意的工人wi,在每次迭代中被选中的概率服从如下分布
(8)

Pri(bi)=
(9)
最后更新获胜者集合U,已完成任务集合RU和候选工人集合Re(行11)。
(3)报酬计算阶段。
在报酬计算阶段,每个获胜者wi∈U的报酬计算为
(10)
3 激励机制性质分析
本节从理论角度分析隐私保护众包软件测试激励机制的性质。
定理5隐私保护众包软件测试激励机制的时间复杂度为O(mn)。
证明算法1第3~12行的while循环中,总共包含m个任务,最多迭代m次可以保证所有的测试任务被完成,内层4~6行和7~9行的两个for循环,遍历了所有投标的工人,工人的总数为n,所以算法3~12行的时间复杂度为O(mn)。算法13~16行计算每个获胜工人的报酬,获胜集合U最大工人数为n,所以时间复杂度为O(n)。综上,机制的时间复杂度为O(mn)。
定理6隐私保护众包软件测试激励机制是真实的。
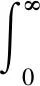
E[pi]=(1-Pri(bi))×0+Pri(bi)×

(11)
根据定理1,可以得出,隐私保护众包软件测试激励机制是真实的。
定理7隐私保护众包软件测试激励机制是个体理性的。
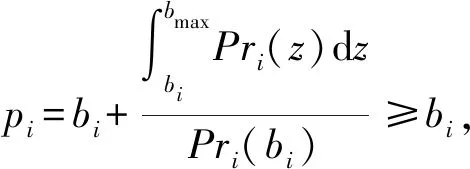
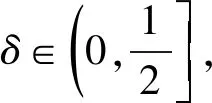
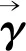
(12)
式中:Wj=W
以下分两种情况讨论。
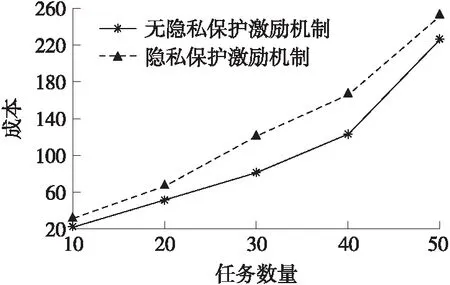
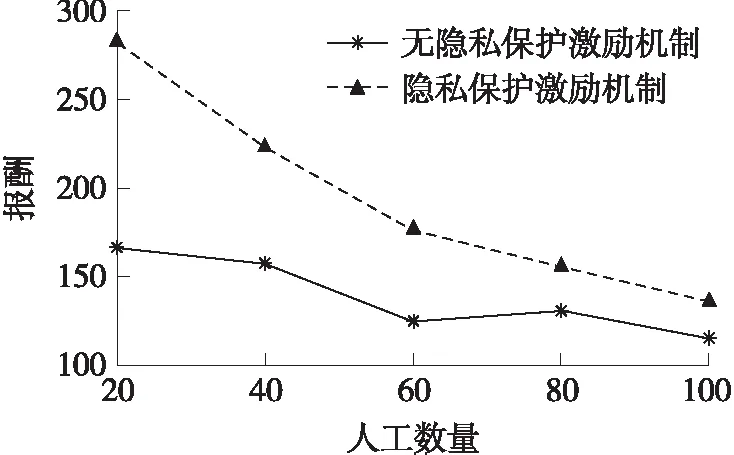
情况1当bd (13) 情况2当bd≥b′d,当j∈[1,l],并且任意工人wj=wd时,第一项小于1,否则第一项等于1,综上,第一项的最大值为1,所以有 (14) (15) (16) 至此,定理得证。 证明令U*表示测试成本最小化问题的最优解,假设有一系列获胜者工人被本文提出的算法选中,即U=w1,w2,…,wl。 对于每个wi,1≤i≤l,假设Ui表示工人集合,此集合满足∀j∈Ui: (1)j∈U*; (2)Tj∩Twj≠∅; (3)Tj∩Twk=∅,∀k∈[1,i-1]; Ui表示部分工人集合,Ui中的工人在U*中,但是由于工人wi的原因不在U中。根据定理6证明的真实性,有bi=ci。根据定理3,取α=t,有至少1-e-t的概率得到 (17) 这表示可以以最低1-e-t的概率得到 (18) 将所有的j∈Ui求和,可以得到以最低1-e-t的概率得到 (19) 最后,对所有的wi∈U求和可以得到 (20) 本节测试隐私保护众包软件测试激励机制的性能。试验部分设计一个无隐私保护的众包软件测试激励机制作为对比算法,此机制的目标是在完成所有测试任务的情况下保证最小测试成本,并且不考虑工人的报价隐私。试验参数设置如表1所示。 表1 试验参数设置 本文通过3个指标测试隐私保护众包软件测试激励机制的性能:总招募成本、总报酬和隐私泄露。 (1)总招募成本:所有获胜工人的总成本。 (2)总报酬:所有获胜工人获得的报酬之和。 (21) PL的值越小,攻击者越难分辨出两个标书集合,隐私保护效果越好。 图1和图2分别比较了在不同任务数量下和不同测试工人数量下的招募工人的总成本。从图1中可以看出,随着任务数量的增加,两种算法的招募工人的总成本均增加。因为增加任务数量,平台需要招募更多的工人完成任务,所以总成本会增加。与图1不同,招募工人的总成本随着工人数量的增加呈下降趋势。因为当参与测试任务的测试工人增加时,平台可以选择更便宜的工人完成任务,所以招募工人的总成本会下降。由于无隐私保护的众包激励机制不需要考虑工人的隐私保护,所以其总成本最低,而本文提出的隐私保护众包激励机制通过概率选择测试工人,可能会招募到选择标准r较高的工人,所以本文的招募工人总成本高于无隐私保护的众包激励机制。本文提出的隐私保护激励机制的总成本比无隐私保护激励机制的总成本平均高出27.31%。 图1 不同测试任务数量下的总成本 图2 不同测试工人数量下的总成本 图3和图4分别测试了在不同测试任务数量和测试工人数量下平台需要支付的总报酬。平台支付的总报酬随着任务数量的增加而增加,更多的任务意味着招募更多的工人,平台需要支付更多的报酬。测试工人的数量增加,使得平台能够选择价格更低廉的工人,那么支付的总报酬也随之降低。定理7中证明了任意工人的效用是非负的,因此,实际支付给测试工人的报酬是不低于其报价的,图3和图4中的总报酬在相同的情况下是分别高于图1和图2中的总成本的,试验结果与理论相符合。 图3 不同测试任务数量下的总报酬 图4 不同测试工人数量下的总报酬 图5分别测试了隐私预算ε对招募工人的总成本以及测试工人的隐私泄露的影响。从图中可以看出,工人隐私泄露的概率随着隐私预算的提高而上升,较大的隐私预算使得隐私泄露PL的值增加,攻击者能够通过输出发现两个邻居数据集之间的差异,使得工人的隐私泄露的可能性增加。而较差的隐私保护,使得平台能更精确地找到选择标准r最小的测试工人,所以招募工人的总成本随着隐私预算的增加而降低。 图5 不同的隐私预算下的总成本以及隐私泄露 本文提出了一种隐私保护众包软件测试激励机制以防止激励攻击并保护工人的测试成本隐私。文章通过理论分析证明了本文的激励机制能够保证计算有效性、真实性、个体理性以及差分隐私性,试验结果表明本文的激励机制平均牺牲了27.31%的招募成本以保证工人的隐私安全,理论结果和试验结果相符合,为众包软件测试的隐私保护领域提供理论依据。在未来的工作中,将考虑根据每个工人的实际需求,为每个工人提供个性化的隐私保护。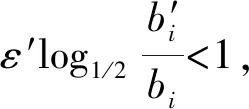


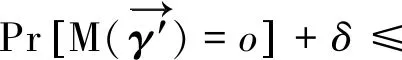


4 性能评估
4.1 试验设置

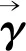
4.2 总招募成本
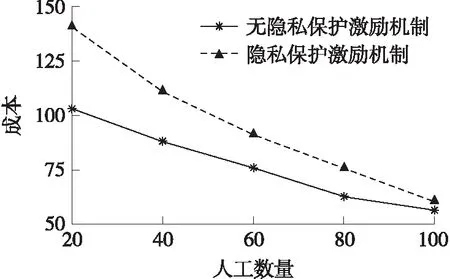
4.3 总报酬

4.4 隐私泄露

5 结束语

