基于人工蜂群优化循环神经网络的财务危机预测

李珊珊,何栋炜,林丹楠,许 萍,任 艳

(福建商学院 1.财务与会计学院;2.信息工程学院,福建 福州 350012;3.厦门大学 信息学院,福建 厦门 361005;4.福州大学 经济与管理学院,福建 福州 350003;5.新疆财经大学 信息管理学院,新疆 乌鲁木齐 830012)

财务运营情况关系着企业的未来发展。由于市场竞争的存在,企业不仅要时刻关注自身经营状况,还需要紧密联系市场大环境中本行业领域的整体经营数据,特别是上市公司的整体经营数据。财务的预测分析作为财务管理的先验手段[1],可以有效规避运行风险,根据预测结果提前采取应对策略,所以预测分析既对自身帮助巨大,同时也便于监管层对上市的经营情况进行有效监测。由于运行所涉及的数据复杂且数据量大,因此通过大数据分析和深度学习算法来解决财务的预测分析问题显得非常有意义[2]。

预测离不开经营过程中产生的大量关键财务指标数据,通过对指标数据进行准确提取和有效处理,为预测提供数据支持,然后采用大数据处理算法对样本数据进行深度挖掘。当前,采用深度学习方法对危机预测的研究成果较多。刘子君等[3]采用支持向量机分类器来对财务状况进行预测,能够实现简单指标的经营预测,预测准确率对指标数量的依赖性强;张亚男等[4]采用极限学习机进行预测分析,并对极限学习机进行粒子群优化,以提高预测准确率,此方法对样本的时间段选择要求高,预测准确率受时间因素影响显著,预测准确率的稳定性有待加强。上述研究结果均指出财务危机预测是根据历史时间段的经营数据经过算法训练后获得的结果,有较强的时间跟踪性,而且指标复杂多变。前者的财务预测准确率受限于财务预测指标,对全面指标评价预测性能不高,而后者的预测准确率又随着财务样本的时间序列选择不同而出现震荡。

因此,为了获得准确的危机预测结果,需要对当前时间前的若干时间段进行分析处理,且能够处理复杂多维预测指标特征。在处理时间序列训练较复杂的问题时,循环神经网络(Recurrent neural network,RNN)表现出了一定的优势,因为RNN能够更加自由和动态地获取输入的信息,而不受到定长输入空间的限制。因此,本文引入RNN来训练样本,并采用差异化时间序列的赋权策略,记忆不同历史时间序列对RNN预测分析的影响。本文的主要创新之处在于:RNN的性能十分依赖历史时间序列权重,此参数的选取直接影响其最终的预测精度。因此,为了进一步提高RNN应对大量财务指标数据的适应度,采用人工蜂群(Artificial bee colony,ABC)算法对RNN的历史时间序列权重进行优化改进,通过反向传播优化各时间序列的权重矩阵,获得稳定的财务危机预测模型。最后通过试验，将所提算法和常用预测算法对比,验证所提算法的预测准确率,证明其有效性。

1 预测指标的选取

财务预测分析的关键问题是指标的合理选取与精准的分析模型,两者缺一不可,而且均对分析预测的准确率有显著影响。经营过程中产生的数据较多,选择能够全面反映运行情况的重要指标和关键数据是危机预测分析的基础,通过多篇文献参考,选取了影响财务状况的关键指标如表1所示[5]。

表1 财务预测指标

表1中提取了财务运行过程中的17个核心指标。通过对比发现,这些指标中,有些指标存在着强关联性,因此在实际分析时,可以进一步采取去耦合分析和弱关联策略[6]。一方面是降低强关联指标所带来的重复运算而降低分析效率;另一方面,高维特征训练分析会无形提升财务危机预测模型的复杂度。去耦合操作后x6和x7之间仅保留x6,x3和x4之间仅保留x3,从而进一步精简了参与RNN的运算变量。

获取财务指标后,需要对指标进行预处理,对一任意指标xi,其处理方法为

(1)

式中:xmin和xmax分别为该指标的最小和最大值。

在完成财务分析指标的选择及去耦合处理后,预测模型的数据样本还要充分考虑数据的时间效应,利用历史数据分析未来财务的运营状况时,应充分挖掘历史数据的影响。在对历史数据分析时,需要考虑到历史数据的时间段长度。本文选择了RNN算法,RNN算法的特点是能够充分利用历史数据进行预测分析。

2 基于ABC-RNN的危机预测方法

2.1 RNN算法

设有n个点xi(i=1,2,…,n)经过RNN的输入权重化及偏置处理后,可得到[7]

(2)

式中:wi(i=1,2,…,n)为各个节点所对应的权重系数,b为偏置常量。

将激活函数作用于经过权重化和偏置处理后的节点得到

(3)

RNN的核心思想便是其隐藏层的循环结构。设x和o分别为RNN的输入与输出,s为隐藏层激活后的结果,具体循环结构见图1。

图1 RNN结构

图1中ot的值不仅与xt有关,还与st-2、st-1有关,而st-2和st-1分别来自于xt-2和xt-1所对应的隐藏层输出。这种t时刻的输出不仅来自于t时刻的输入,还受到t时刻前若干时刻隐藏层输出的影响,通过隐藏层输出的时间序列叠加处理,这正是RNN的核心内涵。图1中U、V和W表示各隐藏层的连接权重矩阵,设样本xt经过隐藏层之后,同时结合前一时刻的输出,经过激励后为[8]

st=f(Uxt+Wst-1+ht)

(4)

式中:f(·)和ht分别为隐藏层激励和偏置。s(t)经过输出g(·)激励后,得到[9]

ot=g(Vst+bo)

(5)

式中:偏置bo为偏置常量。

结合式(2)和式(3),从t时刻进行前向迭代,而迭代过程中ht和bo作为常量不用参与,则有[10]

ot=g(Vst)=Vf(Uxt+Wst-1)=

Vf(Uxt+Wf(Uxt-1+Wst-2))=

Vf(Uxt+Wf(Uxt-1+Wf(Uxt-2+Wst-3)))=

Vf(Uxt+Wf(Uxt-1+Wf(Uxt-2+

Wf(Uxt-3+…))))

(6)

RNN通过不断循环迭代求解,对t时刻前的数据进行权重化循环求解,从而提高输出的时间记忆性,提高深度网络训练的有效性。

采用RNN运算,第k个节点的输出为yk,则误差δk为[11]

δk=(dk-yk)yk(1-yk)

(7)

式中:dk为实际值。

RNN的权重更新为[12]

(8)

式中:η为学习率,hj表示输出。当前权重wjk(n)调整后的权重wjk(n+1)为

wjk(n+1)=wjk(n)+Δwjk(n)

(9)

偏置Δbk(n)的更新方式为

(10)

式中:α为更新步长,一般设置α=1。

当前偏置bk(n)调整后的偏置bk(n+1)为

bk(n+1)=bk(n)+Δbk(n)

(11)

所有节点误差E为

(12)

当E满足设定的阈值,迭代停止,按照此法继续反向求解V、bo和U,W表示前时间序列对当前时刻的权重影响,可灵活设置,本文设置为参与计算的时间序列的倒数。确定了U、V、W和bo之后,便获得了稳定的RNN模型。

2.2 ABC优化的方式

ABC算法主要是根据蜜源的搜寻路径来寻找最优解,现对ABC算法进行数学描述,设蜜源为i,引领探测蜂在第d维的初始随机位置为Xid,其位置具体为[13]

Xid=L〗d+rand(0,1)(Ud-Ld)

(13)

式中:Ud与Ld分别为蜜源在第d维搜索的边界上下限范围,d∈{1,2,…,D},D表示总维度。

探测蜂在Xid处展开蜜源搜索,新蜜源为Vid,其搜索方式为[11]

Vid=Xid+φ(Xid-Xjd)

(14)

式中:j≠i,φ取值范围为[1,1],Xjd为搜索范围内第d维除了Xid外的任意位置。

当探测蜂探测到新蜜源时,会将新旧蜜源进行质量对比,对比方式为计算两者的适应度值,新蜜源Vi=[Vi1,Vi2,…,Vid]的适应度值fiti的计算方法为[12]

(15)

式中:fi为新蜜源的质量。若Vi的适应度值优于Xi,则用新蜜源替换掉原蜜源。

探测蜂将蜜源数据传达至跟随蜂,而跟随蜂选择其偏好的蜜源概率pi为[13]

(16)

探测蜂搜索蜜源的策略为:当迭代次trial达到最大次数Itrmax时,则重新跳转至式(13),否则继续找最优蜜源。

(17)

在RNN网络的反向传播过程中历史时间序列权重的更新通常采用梯度下降算法,存在易陷入局部极小值的缺点,无法获得全局最优的训练目标。因此,本文采用具有较强的全局寻优性能的ABC算法对深度RNN网络的权重进行优化,优化的关键内容在于将RNN网络输出值与预测值的均方误差作为ABC的适用度函数。ABC适用度函数的值越小表示所对应粒子的寻优性能越好,这里选用均方误差(Mean-squared error,MSE)表示

(18)

2.3 财务危机预测流程

根据财务指标数据获取危机预测样本,然后按照式(1)对所有样本的指标进行预处理,最后通过ABC-RNN训练获得危机预测模型,具体流程如图2所示。

图2 基于ABC-RNN的财务危机预测流程

3 实例仿真

为了验证ABC-RNN在财务危机预测中的性能,进行实例仿真。仿真数据来源为某投资管理平台中的上市公司,其主要结构如表2所示。首先对危机预测结果进行可视化,其次对不同时间因素影响的危机预测性能进行仿真,最后采用常用危机预测算法和本文算法进行比较,分别验证其预测性能。特殊处理(Special treatment,ST)类型的公司是指连续两年亏损的公司。

表2 样本集

ABC-RNN的财务状况正常预测标签为0,否则为1。默认选择T-2年度对T年进行预测分析。

3.1 预测可视化

首先采用ABC-RNN对258个训练样本进行预测训练,获得稳定的RNN模型,然后对86个测试集进行财务危机预测,其可视化结果如图3所示。

从图3可清楚得到86个测试样本的财务预测结果,通过观察发现,大部分样本的期望值和预测值吻合,但也出现了8个期望值和预测值不相同的样本,表明这8个样本预测错误。两类的预测结果统计如表3所示。

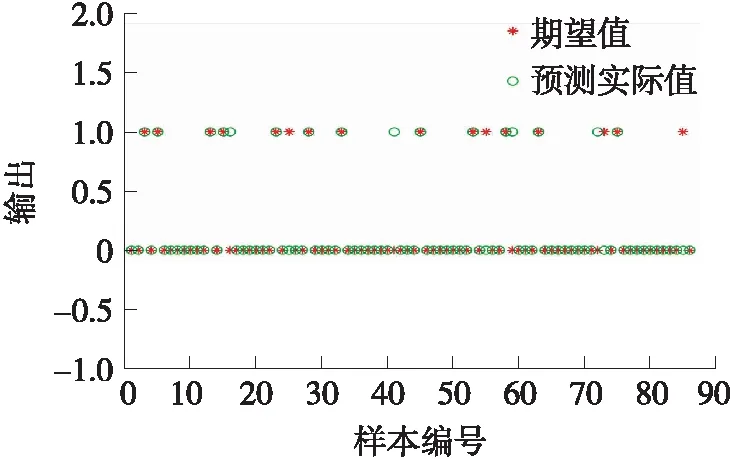
图3 财务危机预测结果可视化

表3 预测结果

从表3知,非ST公司的预测达到了92.8%,而ST公司的预测仅为81.25%,这表明算法对ST公司的预测准确率不是特别高,这可能是因为选择预测历史数据导致的。因为大部分ST公司主要是近2年的财务数据差造成的,而本文选择的参与RNN循环的时间样本正好是T-2年数据,可能造成预测偏差。因此下面将选择不同时间段的样本进行ABC-RNN仿真。

3.2 不同时间段的样本性能仿真

为了验证样本时间段选择对ABC-RNN财务危机预测的影响,分别选择不同年度运行数据作为样本训练,其86个测试样本的预测结果统计如表4所示。

表4 不同时间段的预测结果

从表4可知,从不同时间段获取的财务运行样本对RNN财务危机预测结果影响较大,特别是对ST的预测结果影响较大。这表明相对于非ST,ST的财务预测对样本的时间序列影响更敏感。为了深入分析不同时间段对财务危机预测的具体影响,分别对预测准确率及其均方误差、F值、曲线下面积(Area under curve,AUC)性能进行仿真,结果如表5所示。

表5 不同时间段的预测性能对比

对比得到,在预测准确率方面,选择T-4～T-2年的指标时各类样本数据进行RNN预测效果最好,达到了96.51%,T-3～T-2年的预测准确率次之,为95.35%,T-5～T-2年预测效果最差,仅为89.53%。这表明样本时间段的选择对RNN的危机预测效果影响显著,在采用RNN对危机预测时,既要充分挖掘历史数据对当前预测的影响,也要排除过长历史数据对当前预测的干扰。对比T-4～T-2年和T-3～T-2年的结果发现,两者的均方误差和F值性能非常接近,而在财务危机预测准确率方面,前者更优。但是在AUC性能方面,后者更优,表5表明选择T-3～T-2年进行分析更容易获得财务是否出现危机预测分类结果。因此在选择历史年份数据进行危机预测时,需要更充分考虑。

3.3 不同算法的财务预测性能

为了对比不同算法的财务危机预测性能,分别采用反向传播神经网络(Back propagation neural network,BPNN)[14]、卷积神经网络(Convolutional neural network,CNN)[15]、RNN[16]和ABC-RNN算法对数据进行仿真,历史数据均选择T-3～T-2年,其结果如图4所示。

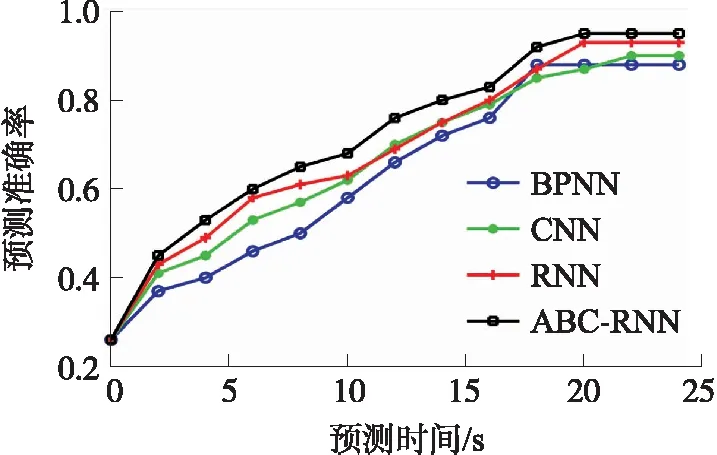
图4 4种算法的预测准确率

从图4可以看出,ABC-RNN算法对表2中的样本预测准确率最高,达到稳定时约为0.95,RNN算法次之,BPNN算法最差,仅为0.88。从预测时间方面来看,BPNN预测效率最高,大约需16 s,ABC-RNN和RNN次之,CNN最差。

下面继续对4种预测算法的AUC性能进行仿真,将BPNN、CNN、RNN和ABC-RNN编号为1、2、3和4,分别进行10次仿真求解其AUC值,结果如图5所示。

图5 4种算法的AUC性能

从图5知道,ABC-RNN算法的AUC值最高,约为0.95左右,RNN次之,BPNN最差。从AUC的稳定性看,ABC-RNN算法的多个AUC值更聚集,BPNN和CNN算法AUC值较分散,而RNN算法的AUC值有个跳变点,表明此算法的预测分类稳定性有待加强,这一结果验证了本文开头对典型RNN稳定性有待改善的分析,这是因为RNN网络的反向传播过程中历史时间序列权重的更新通常采用梯度下降算法,存在易陷入局部极小值的缺点,无法获得全局最优的训练目标。然而,本文提出的ABC-RNN解决了这个问题,借助ABC较强的全局寻优性能并通过合理选择适应度函数,最终获得了稳定且准确的预测结果。

4 结束语

采用ABC-RNN算法对数据样本进行训练,可以获得预测结果,根据预测值可实现对财务预判。相比常用深度学习算法,RNN算法能更充分利用时间序列的循环计算优势,提高了危机预测准确率。此外,为了进一步提高RNN应对大量财务指标数据的适应度,采用ABC算法对RNN的历史时间序列权重进行优化改进,通过反向传播优化各时间序列的权重矩阵,获得稳定的财务危机预测模型。结果表明,和常用预测算法对比,所提ABC-RNN算法的预测准确率更高,且AUC值更高。后续研究将进一步优化RNN算法的隐藏层数和参与运算的各历史时间序列权重,以优化RNN的危机预测效率,提高RNN算法在财务危机预测中的适用度。