基于调频傅里叶变换的改进型鉴相测速

吴佳宁， 葛俊祥， 杨 帆

(南京信息工程大学电子信息技术与装备研究院， 江苏南京 210044)

0 引 言

目前飞行器种类繁多且机动灵活，雷达探测环境愈发恶劣，因此提高雷达探测精度有助于发现并识别目标，在空间监视和精确制导领域有极高的研究价值。另外目标运动参数的精确测量能够改善雷达对目标细微运动的捕捉能力，进而提取目标的微动特征。

鉴相测速是一种通过相邻两帧回波信号的相位差求解目标速度的方法，能够达到波长级的测量精度。鉴相测速的研究重点包括相位提取和解相位模糊。文献[3]介绍了一种改进相位差测距算法，具有运算量小、信噪比门限低的优点。文献[4]介绍了一种调频步进信号的鉴相测速方法，并利用最小波形熵法减小测速误差。文献[5]介绍了一种太赫兹高分辨鉴相测速方法，该方法可以在短时间内实现对目标的高精度测速。文献[6]介绍了基于线性调频信号的高速目标鉴相测速模型，具有较高的测量精度。文献[7]介绍了去斜线性调频信号的鉴相测速模型，但是其研究对象为静止目标，如果目标发生运动时，就需要较高的补偿精度。文献[8]介绍了基于宽带步进频信号的鉴相测速技术，提出了多帧解相位模糊法，该方法能够显著降低对信噪比的要求，但不适用于脉冲重复周期变化的波形。

在以上研究基础上，本文提出了一种基于调频傅里叶变换的改进型鉴相测速方法。首先对回波信号进行互相关FFT处理，提取峰值点得到模糊相位；其次对互相关FFT结果进行调频傅里叶变换，得到速度和加速度的粗估计值；然后根据单帧解相位模糊法，对模糊数修正值进行遍历，找出最优解，得到优化后的解模糊相位；最后采用鉴相测速，得到速度的精确值。

1 回波模型

以线性调频脉冲体制雷达为例，建立回波模型。假设发射的第帧信号为

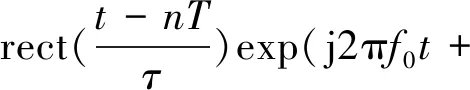
jπ(-)]

(1)

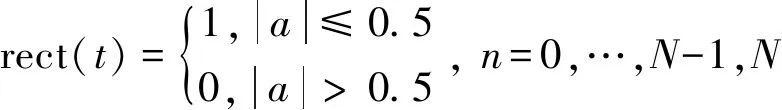
已知光速为，则最大不模糊距离的表达式为

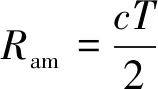
(2)

由式(2)可以看出，最大不模糊距离是由脉冲重复周期决定的。假设脉冲重复周期发生变化，且互为质数，则能够有效改善距离模糊现象。

假设目标沿着雷达发射方向运动，初始距离为，初始速度为，加速度为。设置脉冲重复周期发生变化，令表示第帧信号的脉冲重复周期。对于第帧回波信号，目标相对雷达的瞬时距离和速度分别为

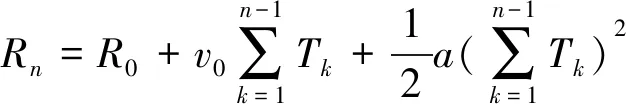
(3)

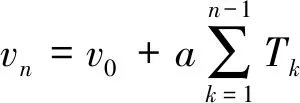
(4)

不考虑噪声信号和外界干扰，则雷达接收到的基带回波信号为

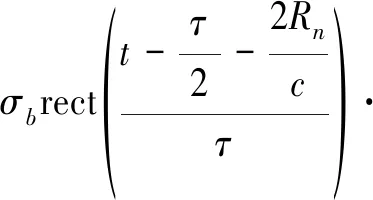
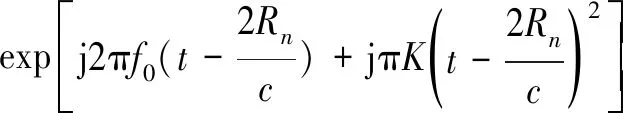
(5)

式中，为雷达散射系数。

对()进行去斜处理，假设参考信号为

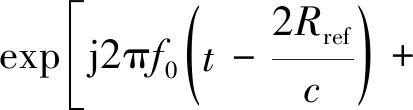
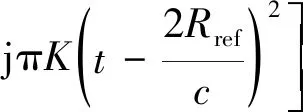
(6)

式中，为参考距离。

去斜处理后的混频信号为

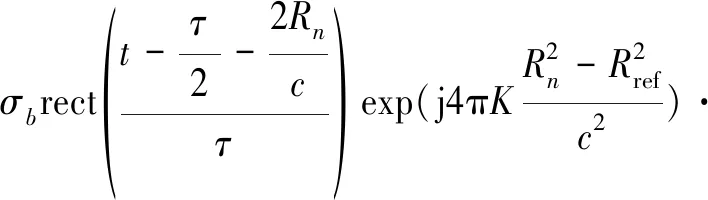
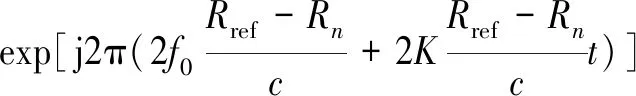
(7)

由式(7)可以看出，混频信号中存在二次相位项，在合成高分辨率距离像时会造成散焦现象，因此需要对其进行补偿处理。

对二次相位项进行补偿处理，并计算相邻两帧信号的互相关FFT结果为

FFT{+1()·()}=

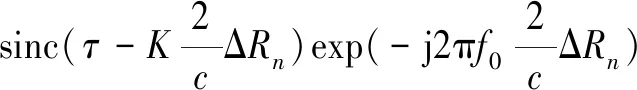
(8)

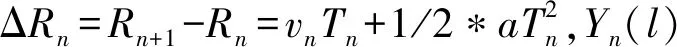
由式(8)可以看出，互相关FFT结果的包络为sinc函数，其相位项包含速度和加速度信息。通过提取峰值点，再进行鉴相测速可以得到高精度的测量结果。

2 基于调频傅里叶变换的改进鉴相测速方法

2.1 调频傅里叶变换定义

调频傅里叶变换是匹配傅里叶变换的一种极坐标形式，在低信噪比条件下具有良好的测量性能。由于其变换核是线性调频函数，故对于线性调频信号来说是一种线性变换。

假设一个二次相位信号为

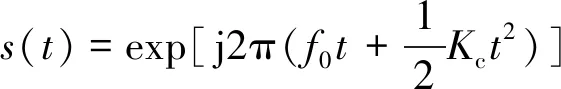
(9)

其调频傅里叶变换为

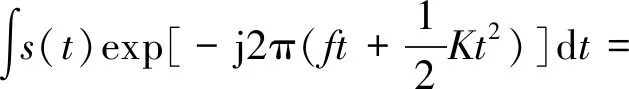
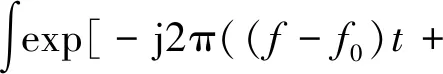
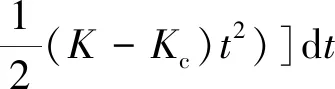
(10)

式中，和为调频傅里叶变换的参数。

由式(10)可以看出，当=且=时，在-二维图谱中会出现相参积累峰值，其本质是变换核的自动匹配。如果能够完全匹配，则信号能量达到峰值；反之如果没有完全匹配，则信号能量相互抵消。

由于调频傅里叶变换需要二维搜索，运算效率低，可以对式(10)进行修改：

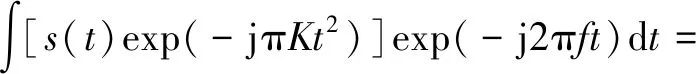
FFT{()exp(-jπ)}

(11)

由式(11)可以看出，调频傅里叶变换相当于先对信号进行解调频处理，再进行FFT操作，这样能够将二维搜索简化为一维搜索，提高运算效率。

2.2 鉴相测速原理

已知相邻两帧回波信号的目标距离为Δ，速度为，时间差为Δ，相位差为Δ，波长为，则满足以下关系式：

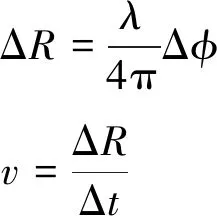
(12)

由式(12)可以看出，鉴相测速的测量精度可以达到波长级，目标速度与相位息息相关。如果能够提取到目标的准确相位，就可以计算出目标速度的精确值。

分析式(8)中的峰值点相位：

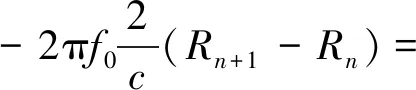
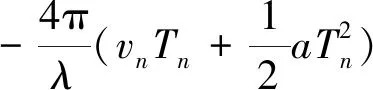
(13)

通过化简可以得到鉴相测速结果：

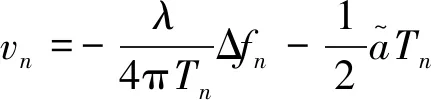
(14)

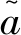
由于从互相关FFT结果中提取到的是模糊相位，不能直接用于鉴相测速。因此，鉴相测速的关键是如何得到精确相位，即解相位模糊。假设Δ为模糊相位，Δ为解模糊相位，为模糊数，则满足以下关系式：

Δ=2π+Δ

(15)

目前，解相位模糊的方法主要包括单帧解相位模糊法和多帧解相位模糊法。其中，单帧解相位模糊法比较常用，且易于实现，其具体流程为：

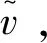
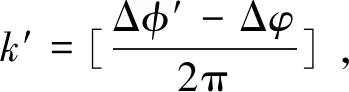
3) 最后计算得到精确相位Δ=2′+Δ。

多帧解相位模糊法利用多帧回波信号求解模糊数，但该方法需要脉冲重复周期保持不变，限制了其应用场景。因此，本文将采用单帧解相位模糊法。

在低信噪比的条件下，传统鉴相测速的结果不理想。其主要原因是：第一，低信噪比造成峰值点提取不准确，无法得到精确相位；第二，低信噪比导致传统鉴幅测速精度较差，无法正确解相位模糊。针对在低信噪比条件下鉴相测速无法使用这一问题，可以引入模糊数修正值，通常∈[-2,-1,0,1,2]，遍历的每个取值，比较其对应的测速误差，找出最优解′，这样能够降低鉴相测速对信噪比的要求。

2.3 改进型鉴相测速方法流程

1) 对第帧回波信号进行互相关FFT处理，提取峰值点，得到模糊相位Δ；

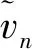
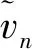
4) 引入模糊数修正值，修正后的模糊数为+，遍历的每个取值，比较其对应的测速误差，找出最优解′；

5) 优化后的解模糊相位Δ=2π(+′)+Δ，根据式(14)计算出鉴相测速结果；

6) 对每帧回波重复步骤1)到步骤5)，得到所有回波信号的改进型鉴相测速结果。

改进型鉴相测速方法流程如图1所示。

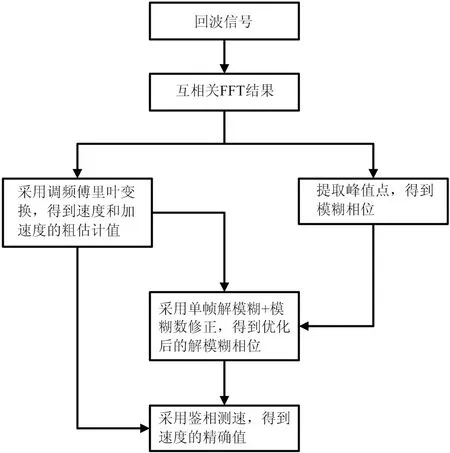
图1 改进型鉴相测速方法流程

3 仿真实验分析

假定目标沿着雷达径向方向作匀加速直线运动，初始距离为1 000 m，初始速度为50 m/s，加速度为20 m/s，一共产生200帧回波信号。雷达的具体参数如表1所示。

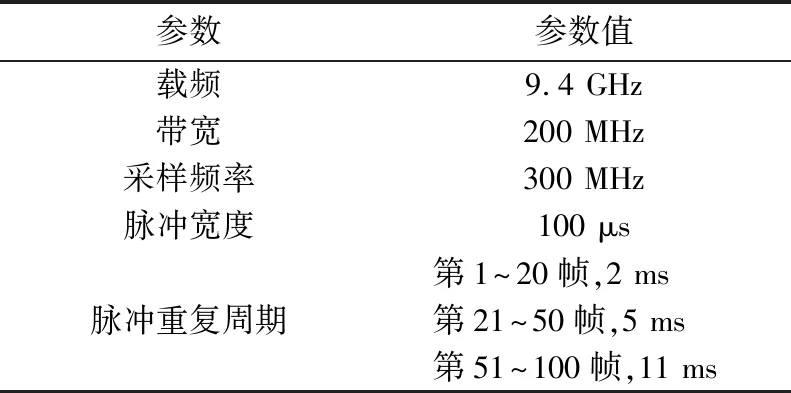
表1 雷达参数

将脉冲重复周期设置为逐渐增大，且互为质数，这样能够减小距离模糊的影响。由于目标是逐渐远离雷达，故将信噪比设置为逐渐减小，第1～20帧回波信噪比为0 dB，第21～80帧回波信噪比为-5 dB，第81～200帧回波信噪比为-10 dB，这样更加符合实际测量情况。

实验1 互相关FFT法速度估计

回波信号的互相关FFT结果如图2所示。由图2可以看出，第1～20帧回波信噪比较高，此时目标的运动路线比较清晰；随着信噪比逐渐降低，目标的运动路线被噪声所掩盖。

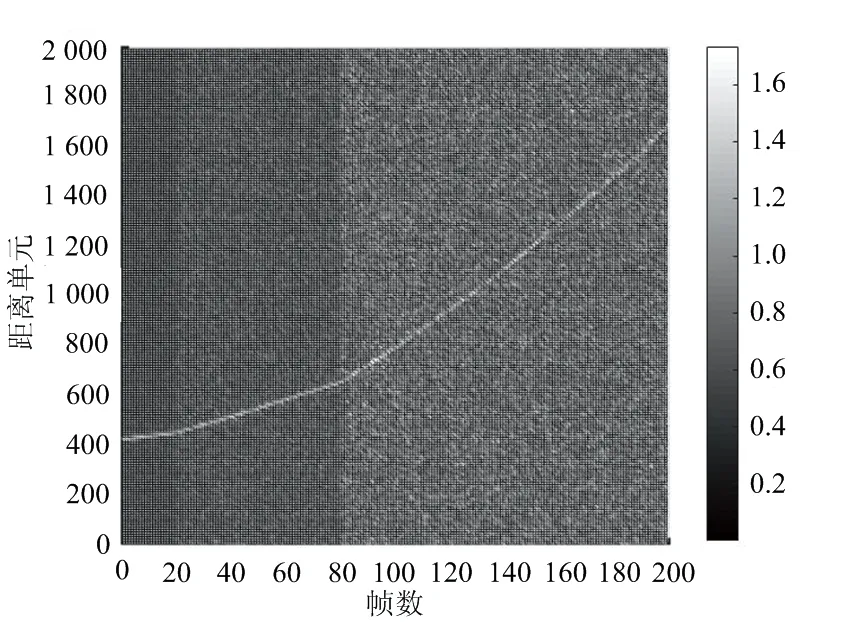
图2 回波信号的互相关FFT结果

因此，需要对互相关FFT结果进行降噪处理。图3为平滑滤波后提取峰值点的结果。平滑滤波可以改善提取峰值点的准确性。

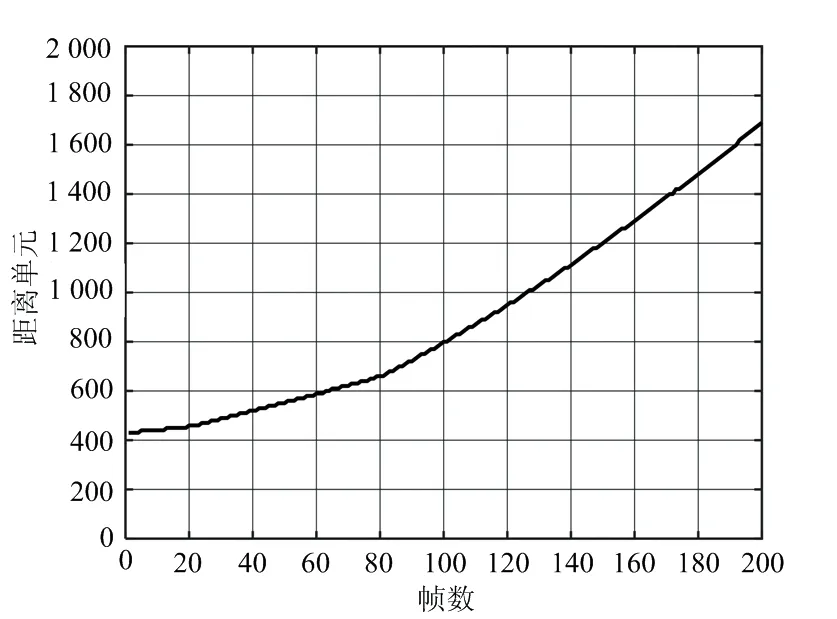
图3 平滑滤波后的峰值点位置

图4为互相关FFT法的测速结果及误差。由图4可以看出，当信噪比为0 dB时，测速误差小于5 m/s；随着信噪比不断降低，测速误差出现大幅度不规则波动，无法满足精度需求。

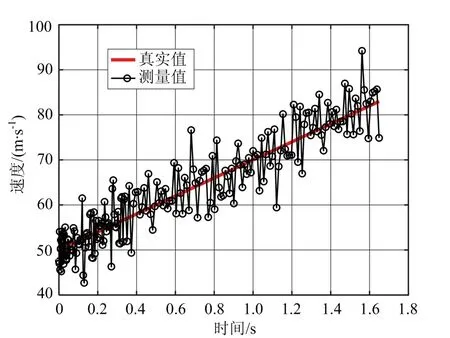
(a) 互相关FFT法的测速结果

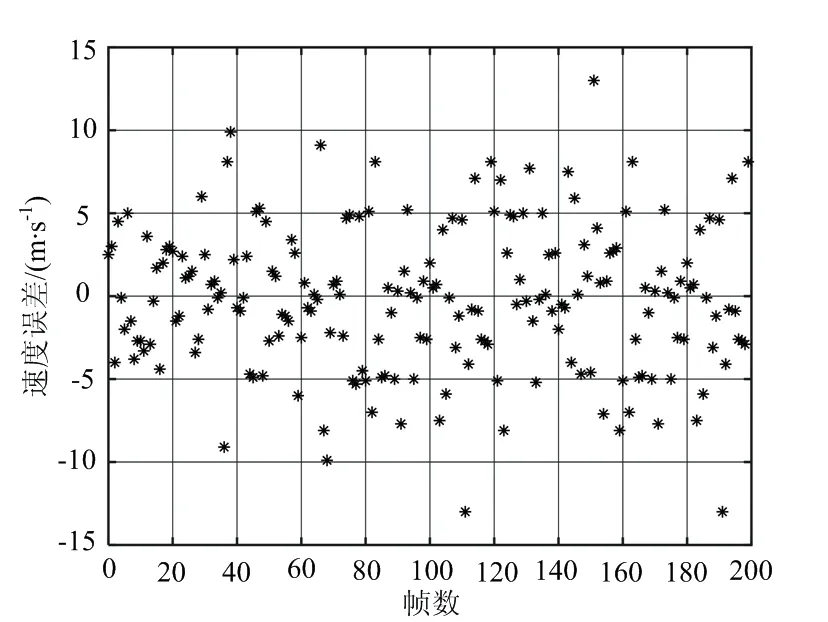
(b) 互相关FFT法的测速误差图4 互相关FFT法的测速结果及误差

实验2 调频傅里叶变换法速度估计

根据互相关FFT结果， 采用调频傅里叶变换法对加速度和速度进行粗估计。 表2和图5为调频傅里叶变换法的估计结果，加速度的粗估计值为21.1 m/s。图6为调频傅里叶变换法的测速误差，可以看出相比于互相关FFT法测量精度有所提高，但是在低信噪比条件下误差仍然较大，需要后续进行鉴相测速加以改善。

表2 调频傅里叶变换法的估计结果

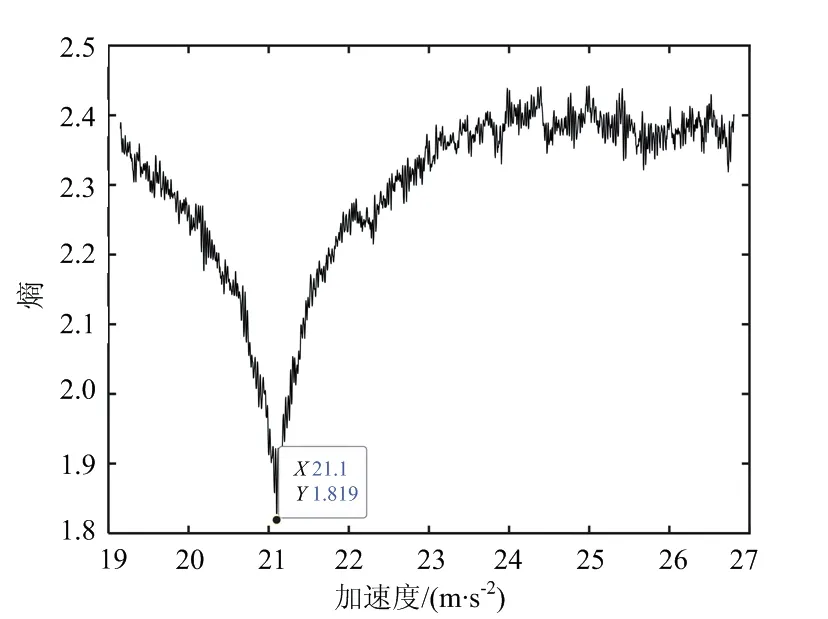
(a) 加速度估计，SNR=0 dB

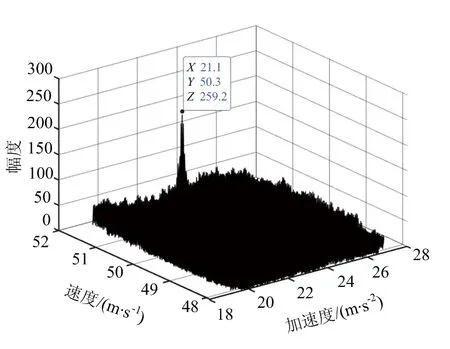
(b) 第1帧回波速度估计，SNR=0 dB

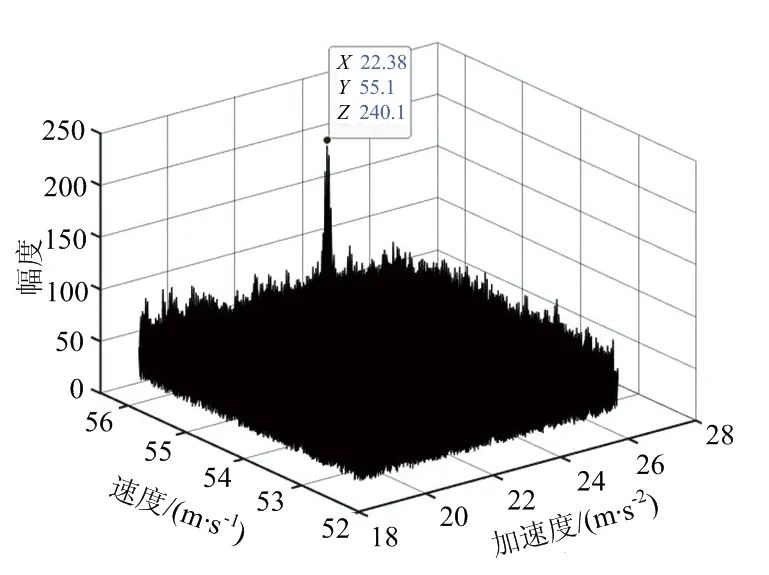
(c) 第50帧回波速度估计，SNR=-5 dB

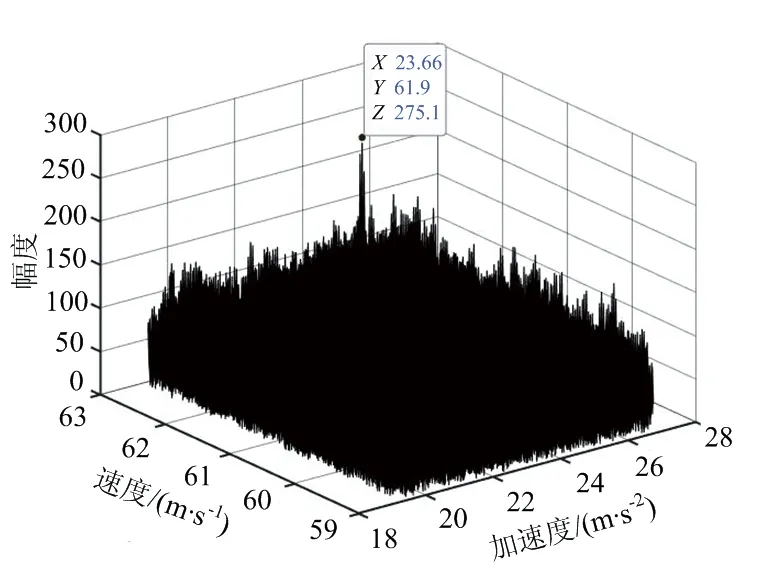
(d) 第100帧回波速度估计，SNR=-10 dB图5 不同信噪比条件下调频傅里叶变换法的估计结果

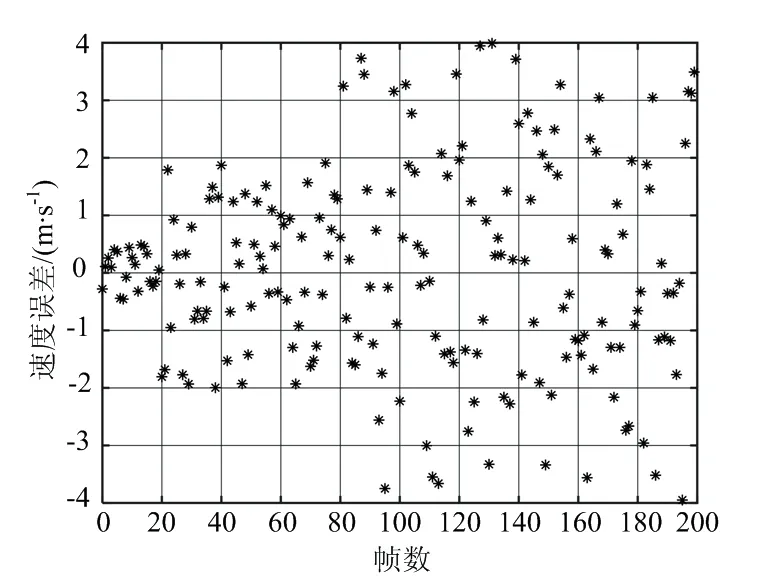
图6 调频傅里叶变换法的测速误差

实验3 改进型鉴相测速法速度估计

根据速度和加速度的粗估计值，采用单帧解模糊相位法，对模糊数修正值进行遍历，找到最优解。图7为改进型鉴相测速结果及误差。将图6和图7(b)进行比较，可以看出在低信噪比条件下,改进型鉴相测速误差小于2 m/s,测量精度显著提高。

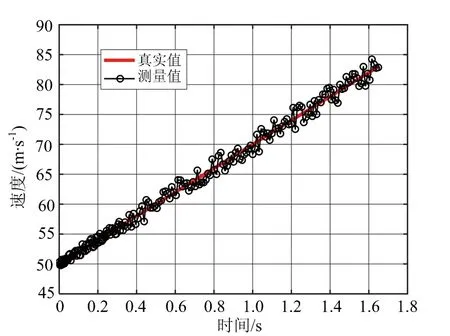
(a) 改进型鉴相测速法的测速结果

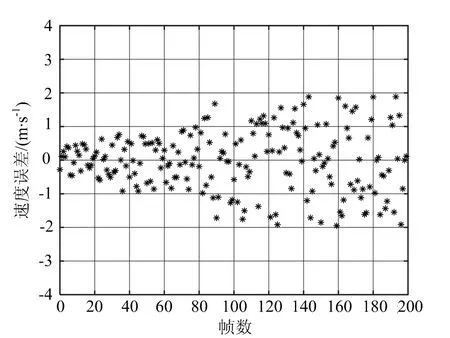
(b) 改进型鉴相测速法的测速误差图7 改进型鉴相测速法的测速结果及误差

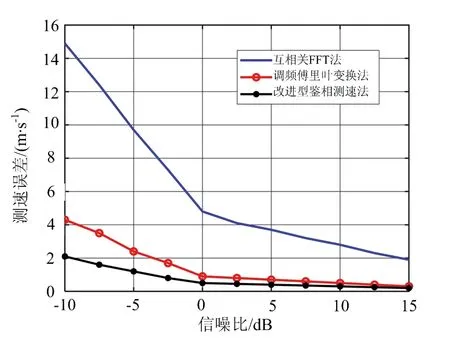
图8 不同方法的测速误差

为了判断在不同信噪比条件下本文所提方法的性能，进行1 000次蒙特卡洛仿真实验。忽略提取峰值点的误差，对比互相关FFT法、调频傅里叶变换法和改进型鉴相测速法。图8为不同方法的测速误差。由图8可以看出，当信噪比较高时，三种方法的测量精度差距不大；当信噪比较低时，互相关FFT法误差急剧增加，调频傅里叶变换法误差稍有增加，改进型鉴相测速法误差增加最少，仍然能够提供高精度的测量结果，验证了其在低信噪比条件下的良好性能。

4 结束语

本文提出了一种基于调频傅里叶变换的改进型鉴相测速方法，该方法首先对回波信号进行互相关FFT处理，提取峰值点得到模糊相位；其次通过调频傅里叶变换法得到速度和加速度的粗估计值；然后根据单帧解模糊相位法，对模糊数修正值进行遍历，找到最优解，得到优化后的解模糊相位；最后采用鉴相测速，得到速度的精确值。仿真实验证明，该方法具有测量精度高、抗干扰能力强等优势。为了进一步降低鉴相测速误差，下一步的工作是改进峰值点提取算法，可以引入相参积累和滤波器技术，以减小噪声的干扰。