基于GA-PSO的六轴机械臂轨迹规划方法

机械臂轨迹规划较为基础的方法主要有两种，其一是关节空间规划，它在运动时可以防止机械臂出现不稳定性和冗余的问题，因此大部分人都用该方法

；另一种是笛卡尔空间规划，该方法相对于第一种较为少用。文献[2]在对机械臂关节空间运动轨迹规划进行阐述时，对照3次和5次多项式中运行空间规划后的优缺点，结果显示3次多项式在运行空间规划时的效果明显低于5次多项式。

为了使机械臂在各性能中的某个目标达到最佳，需要严谨的谋划出一条符合机械臂各关节条件限制的运行轨迹，使其运动性能得以充分发挥。在随机的场景中可对机械臂各个性能进行相应的优化，目前主要优化目标为以下三种：运行时间，关节撞击以及能量损失。本文主要针对运行时间这一方面进行深刻分析及研究。针对此方面，文献[1]和文献[3]对遗传算法进行改进，进而求解出时间最短的运行轨迹，加快了算法的收敛；文献[4]则将遗传算法自适应度提高，从而使其收敛速度变快。文献[5]使用了传统粒子群算法获取到工业机械臂相应时间—脉动的最佳运行轨迹。当今工业机械臂领域中，不同的智能优化算法亦有相应的劣势。例如传统遗传算法主要的缺陷表现在扩展能力不足而且收敛速率相对较慢;粒子群算法的缺点在于容易得到部分最优解。文献[6]在初速度和加速度以及加加速度的限制条件下获取了时间最佳3次多项式运行轨迹。时间最短的前提大多数是通过速度的最大化以及加速度的最大化来实现，不过这样利用极限速度来实现这一指标会使关节的力矩变大，容易导致电机的过流进而严重磨损机构。文献[7]运用改进人工蜂群算法提高收敛速度，但也难以求出实际的全局最优解。文献[8]运用机器人学中的运动学和轨迹规划的知识，提出“3-5-3”混合多项式插值函数的方法进行了对过路径点得起轨迹规划，但对动力学、控制理论部分的研究并没有涉及。文献[9]利用牛顿法搭配埃特金加速法进行优化，得出5次B样条函数插值运动轨迹规划，使其在撞击以及时间方面得到最优解。文献[10]通过实际应用问题分析机械臂的关节角度和速度来达到稳定运行。文献[11]研究出一种限制柔性连杆机械臂振动的轨迹规划方法。文献[12]提出了4-5-4多项式混合插补算法、PSO优化算法并将两种算法相结合的轨迹规划方案，但没有进一步把机器人动力学等相关变量信息一并考虑。

综上可知，在不控制情境的前提下，大班幼儿有很多种同伴交往策略。并且不难看出，以上归类的策略是很多具体交往策略的概括。大班幼儿在进入人际互动时，交往技能还不是很成熟，一些生硬、直接的同伴交往策略的种类还是比较多的，大班幼儿在同伴交往过程中,可能会同时使用几种策略对同一事件做出反应。如：面对同伴的拉扯，他边使劲推开同伴，边大声指责：“你干嘛，走开”。很明显，他在面对同伴的拉扯时，采用了个人攻击、指责和指令策略。

本文提出了一种人工智能算法来对轨迹优化，它的基本流程是先将笛卡尔空间规划予以的相应路径点转化成关节空间运行轨迹的各个点，这种方式可按照关节空间运动规划的流程，运用5次多项式来执行相对应的运动轨迹规划；然后连合GA-PSO混合优化算法进行关节空间中位置和时间优化，获得精确的最优解。

法国分葱代表休伯特·列南（Hubert LENAN）先生在接受本刊记者采访时介绍到，目前分葱主要在法国布列塔尼区和卢瓦尔河地两个大区进行种植，占了法国大部分分葱的产量。法国的分葱主要是在海洋气候下生长，这个地区特有的利摩尔土壤，使得种出来的分葱营养价值更高。首先，分葱完全手工种植，种植深度要求在20厘米-25厘米左右；其次，完全手工采摘；再次，在分葱收获之后要将其在太阳下曝晒两到三周，通过日晒让分葱的营养变得非常集聚、紧实，更有利于保存；最后，用机器对它进行分解、风干，再进入到储存或销售的环节。

1 机械臂的建模

(2)生成原始种群并开始进行适应度值的计算。然后输出目前种群的最优位置和全局的最优位置；

遵循任务的需求准则，机械臂终端须要途经的点Pi(i=1,2,3…N)利用机器人逆运动学得出关节空间规划中相应关节的关节角度

，

则视为第

个关节(

=1,2,3,4,5,6)。设置各个关节的时间序次为

，全部轨迹的初始点和结束点的速率还有加速度的值均为0。本文利用5次多项式的方法对关节角度进行描述。从目标点

到

+1,两个起点位置的限制条件为：

由此得出5次多项式相应插值下路径

、速度

以及加速度

如下：

推荐理由:这是来自畅销书系列《图书馆老鼠》的获奖作者丹尼尔·柯克的一本非虚构的传记绘本。本书引发了人们对于野生动物保护和对世界濒危动物的关注，促进了人们对于动物救助和福利的进一步了解。这个迷人的故事，有助于孩子们对于人类与动物之间关系的了解。

此D-H参数表的

视为关节转角，

视为连杆偏距，

-1

视为连杆长度，

-1

视为连杆转角。由该四个参数即可确立相邻轴间坐标系的转换关系。

2 轨迹规划论述

李达是中共一大的发起者、筹备者、召集者和组织者，他和夫人王会悟也是同时参加党的一大的唯一一对夫妻。在中国共产党早期领导人中，“还很少有像李达同志这样勤奋、这样有丰富的卓越的成就，这样在任何困难危险的环境下生命不息、战斗不止的马克思主义宣传家、教育家，这样坚定勇敢而不断追求进步，力求达到当代的最高水平的马克思主义理论战士”。他为中国共产党的创立，为马克思主义在中国的传播，为丰富毛泽东哲学思想作出了重要贡献。

(3)通过与约束条件进行对比，对当前迭代中的粒子的速度与位置持续进行更新；

(1)

机械臂关节速度的限制条件为：

(2)

ti变量作为此次需要被优化的对象，表示每一节的运动时间，公式(6)作为此次目标函数，公式(7)作为限制的条件，

作为关节

最高速度，

作为最高加速度，

为力矩最高值。利用公式(6)可计算得出在任一时间中机械臂关节运行速度、关节角度以及其加速度，利用公式(1)可计算出关节在任意时刻的力矩，得出的结果放到公式(7)算出机械臂相应运动的约束方程。

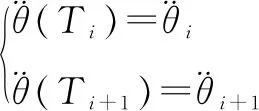
(3)

将限制条件(1)～(3)联立可计算出关节中运动函数里各系数为：

(4)

运用机器人学的逆运动学，利用末端位姿来进行逆运动学求解，从而得到关节空间中的各个关节角度；通过各个轴的角度值进行计算来获得终点位置的方法叫做正运动学。ROKAE机械臂中XB7的D-H参数表如表1所示。

(5)

在提升效率同时还要考虑机械臂的运动学和动力学两个约束问题：

(6)

(7)

机械臂关节加速度的限制条件为：

运用5次多项式的规划方法来阐述机械臂关节角的前提条件是要获取相应轨迹运行所得时间，由于其在已有时间条件下无法进行最优求解，因此使用智能算法进行相应的求解。本文采取GA-PSO混合算法来求解，算法主要流程如下：

(1)设计一个三维搜索空间，生成N个粒子种群，对各粒子的位置与速度进行初始化操作；

本文使用ROKAE的六轴工业机械臂，通过D-H参数法来获取运动学的建模。如图1所示。

确定渠道策略后势必进行经销商队伍的整合与调整，要求新合作伙伴必须具备终端网络资源和操作经验。百雀羚积极与知名KA终端谈判合作，先后进驻了沃尔玛、华润万家、易初莲花、世纪华联、中百仓储等KA类卖场，并进行了终端形象包装。百雀羚的渠道变革很快得到了回报，结果百雀羚推出的草本精粹护肤商超系列，深受消费者的喜爱，销售额高速增长，这都证明了百雀羚渠道选择的正确性。

图书馆工作人员队伍的复杂化导致了图书馆馆员在学历上 参差不齐。虽然不少馆员通过不同的途径加以学习提升了自己的学历，但整体素质依然不高；非专业馆员选择了这份职业后都面临一个角色转换的过程，往往需要经历一个长时间的学习过程，在积累了一定的工作经验后才可以熟悉图书馆的馆藏资源，运用学科知识为师生提供针对性、专业化、深层次的服务。为了更好的满足读者对信息资源的多元化需求，尤其需要专业技术人员对资源的整合集群和协同管理。因此学科馆员在图书馆未来的发展中必定属于中间力量。

(4)输出全局最优解。

3 实验与仿真

通过MATLAB进行仿真，如图2所示为单独使用PSO算法的迭代图，图3为单独的GA算法迭代图，图4为GA-PSO混合算法迭代图。

单独使用PSO算法算法的迭代次数为40次，单独使用GA算法迭代次数为69次，GA-PSO混合算法得出迭代次数则为35次，数据结果显示，GA-PSO混合优化算法相比于单一的传统算法收敛速度更迅速，适应度值更优。

ROKAE机械臂运行时间如表2所示，优化后运行时间减少1.65秒，效率提高了约23.6%

4 结论

本文在将机器人学中相应的运动学以及动力学作为限制条件，放弃3次多项式而使用5次多项式分析ROKAE机械臂每个关节角，提出了一种GA-PSO混合人工智能算法来达到以时间最短作为首要目标的运行轨迹规划。实验数据的结果表明，相比于单独应用GA、PSO算法，使用GA-PSO混合人工智能算法可以使其收敛变得更加迅速，相应得出适应度的值更好。该算法可对ROKAE机械臂进行运行轨迹的优化，在限制了关节位置及其速度，相应的加速度的条件下减少了机械臂运行时间，对比不采用此算法的运行轨迹时间减少约23.6%。

[1]殷凤健,梁庆华,程旭,等.基于时间最优的机械臂关节空间轨迹规划算法[J].机械设计与研究,2017,33(5):12-15.

[2]孙亮,马江,阮晓钢.六自由度机械臂轨迹规划与仿真研究[J].控制工程,2010,17(3):388-392.

[3]曾关平,王直杰.基于改进遗传算法的机械臂时间最优轨迹规划[J].科技创新与应用,2020(22):6-9.

[4]Liao Xiaoping,Wang Weidong,Lin Yizhong,Time-optimal trajectory planning for a 6R jointed welding robot using adaptive genetic algorithms[C]//Proceedings of 2010 International Conference on Computer,Mechatronics, Control and Electronic Engineering (CMCE 2010) Volume 2.Chang Chun:Institute of Electrical and Electronics Engineers,2010:617-620.

[5]沈悦,李银伢,戚国庆,等.基于PSO的工业机器人时间-脉动最优轨迹规划[J].计算机测量与控制,2017,25(1):158-162.

[6]谭冠政,蒋建敏.机器人的时间最优控制轨迹规划[J].湘潭大学自然科学学报，1990,12(02): 106-113.

[7]舒鹏飞.六轴工业机器人的轨迹优化研究[D].合肥:合肥工业大学,2020:26-46.

[8]程浩田.基于正逆运动学分析的机械臂时间最优轨迹规划研究[D].太原:中北大学,2021.49-54.

[9]查文斌，朱永飞，徐向荣，等.一种机械臂时间一冲击轨迹的快速求解优化方法[J].机床与液压,2021,49(9):11-15.

[10]陈梁远，郭丽娟，唐彬，等.一种六氟化硫检测机械臂的设计与分析[J].沈阳理工大学学报,2020,39(3):88-94.

[11]Li Yuanyuan,Sam Ge Shuzhi ,Wei Qingping ,et al. An Online Trajectory Planning Method of a Flexible-Link Manipulator Aiming at Vibration Suppression[J]. IEEE Access,2020,8(1):130616-130632.

[12]任伟.六自由度工业机器人轨迹规划研究[D].芜湖：安徽工程大学，2020:40-66.