离轴三反望远镜轴向与横向失调量像差耦合特性

白晓泉，郭 良，马宏财，许博谦，鞠国浩，徐抒岩

（1. 中国科学院长春光学精密机械与物理研究所, 吉林 长春 130033；2. 中国科学院大学, 北京 100049；3. 中国科学院空间光学系统在轨制造与集成重点实验室, 吉林 长春 130033）

1 引 言

随着人类文明的不断进步，天文学得到了极大的关注，并取得了长足的发展。一大批天文仪器的成功建造，激发了人类对“两暗、一黑、三起源”的探索热情[1]。“工欲善其事必先利其器”，为了看清更远、能量更低的天体，需要提高望远镜的分辨率与集光能力，而提高两者性能的有效手段之一便是增大望远镜的口径。因此，近年来，天文望远镜的口径记录不断被刷新。相比于地基望远镜，空间望远镜不受大气扰动的影响，在天文观测方面发挥着巨大作用。离轴系统相比于同轴系统不存在口径遮拦，在椭率观测等方面具有诸多优势[2]。因此，大口径离轴天文望远系统获得了广泛关注，保证其成像质量具有重要意义。

光学系统的成像质量通常取决于设计、加工以及装调。对于离轴三反系统的设计，科研人员提出了一系列设计方法并设计出了满足不同需求的三反系统[3]。大口径光学反射镜的加工、检测技术也获得了极大的关注，以中国科学院长春光学精密机械与物理研究所为代表的科研机构取得了丰硕的成果[4-7]。大口径镜面易受外热流波动影响而发生曲率半径的改变，针对曲率半径误差，白晓泉、许博谦等[8-9]基于矢量像差理论，先后分析了主镜曲率半径误差对离轴两反望远系统、离轴三反望远系统像差场的影响并提出了具有针对性的补偿策略。对于离轴三反的装调，鞠国浩、顾志远、马宏财等[10-14]对离轴系统装调开展了深入的研究，基于矢量像差理论依次分析了横向、轴向、旋转失调对离轴系统像差场的影响，提出了具有一定价值的地面装调、在轨调整理论，为离轴系统装调打下了坚实的理论基础。

当前，已经建立了基于矢量像差理论的单一失调量对离轴三反像差场影响的解析表达式。然而，不同类型失调量对像差场影响的耦合特性尚未被揭示，定量化的解析补偿关系尚未建立。因此，有必要对像差场耦合特性进行系统性研究，为进一步分析离轴三反像差场特性提供一定的理论指导。

本文针对轴向失调量与横向失调量之间的像差耦合特性，建立了基于矢量像差理论的解析关系，分析了两者耦合对像散、彗差的影响。然后，重点分析了两类特殊的耦合关系及耦合条件，即横向失调引入的像散、彗差与轴向失调引入的像散、彗差的补偿关系（横向失调引入的离焦不能补偿轴向失调引入的离焦）。通过分析补偿前后像差场的分布特征及RMS（Root Mean Square）波前误差的变化情况（忽略离焦），揭示了实际装调可能陷入的误区，也提出了空间望远镜在轨调整策略。最后，通过实验对本文结论进行了合理的验证。

2 轴向失调量与横向失调量耦合的解析关系

2.1 离轴系统矢量像差理论

基于光瞳坐标变换原理[2,15]，离轴反射系统的波像差可表示为：

当系统处于非标称状态（存在误差）时，由Buchroeder 和Thompson 等[16]人研究成果可知，系统波像差可表示为:

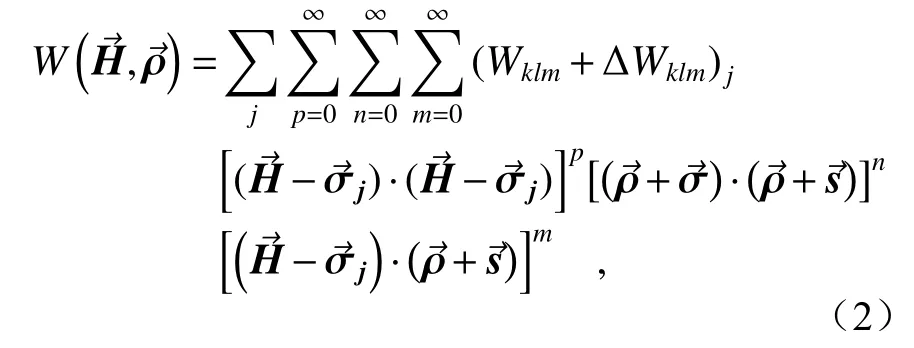
文献[16] 的研究表明：第一，轴向失调主要影响波像差系数，横向失调主要改变像差场偏心矢量；第二，失调主要引起三阶像差，包括离焦、像散、彗差、场曲及球差的改变。因此，式（2）可进一步整理为：

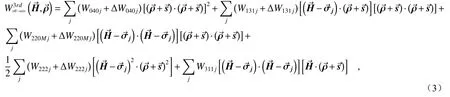
其中，场曲不影响成像质量，球差改变量相对较小，空间望远镜通常配有摆镜用来调整离焦及像面倾斜。因此，失调导致像散场、彗差场的改变成为在轨像质保持关注的焦点。故基于三阶像差理论，仅考虑三阶像散、三阶慧差时，失调状态下系统波像差可进一步表示为[8,17]:

其中：ΔWklm j=KklmjΔdj，Kklmj为特定类型波像差系数关于反射镜轴向失调（ Δdj）的敏感度，其可通过Seidel 像差理论进行解析计算。

2.2 实验与仿真系统

为了验证本文结论的可靠性，本文以实验室现有的一套离轴三反系统为例，进行仿真与实验验证，如图1 所示。该系统入瞳口径为500 mm，光瞳沿y方向的离轴量为-460 mm（即→s=[0,-1.84]T），视场为0.6°×0.4°（视场在y方向偏轴-0.6°），根据解析关系可计算系统各个像差系数敏感度值，如表1 和表2 所示。根据消像散三反望远系统结构特点可知，初级波像差系数对主次镜间距变化比对次三镜间距变化更敏感[18-19]，表1 和表2 也可以间接验证上述结论。因此，在本文讨论中，主要分析次镜轴向间距改变量（ Δd1）对波像差系数的影响。

图1 500 mm 离轴三反光路图。（a）示意图及（b）实验图Fig. 1 (a) Schematic diagram and (b) experiment device of the 500 mm off-axis three-mirror system

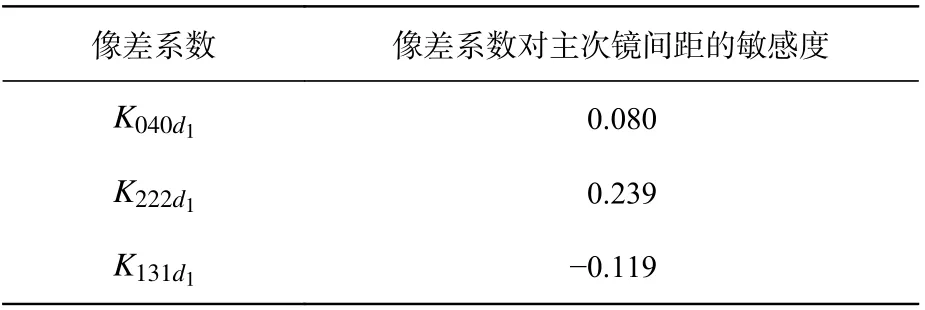
表1 波像差系数对主次镜间距的敏感度Tab.1 Sensitivity of the wavefront aberration coefficient to the distance between primary and secondary mirrors(632.8nm/mm)

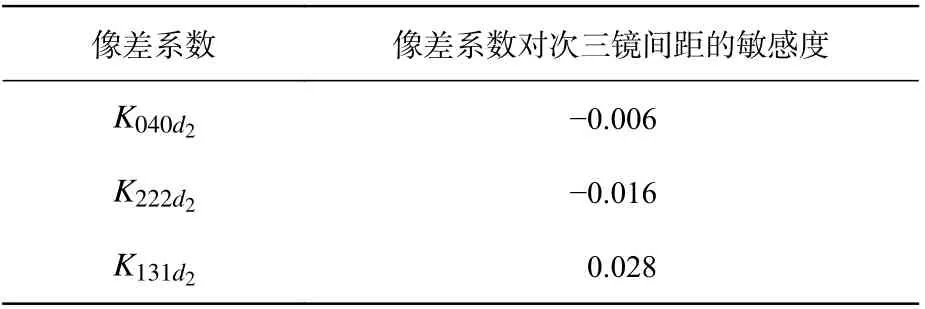
表2 波像差系数对次三镜间距的敏感度Tab.2 Sensitivity of the wavefront aberration coefficient to the distance between the secondary andtertiary mirrors (632.8 nm/mm)

3 两类失调耦合对像差场的影响

3.1 两类失调耦合对像散场的影响

由式（4）可知，当横向失调和轴向失调同时存在时，偏轴离轴三反系统的像散场增量可表示为：

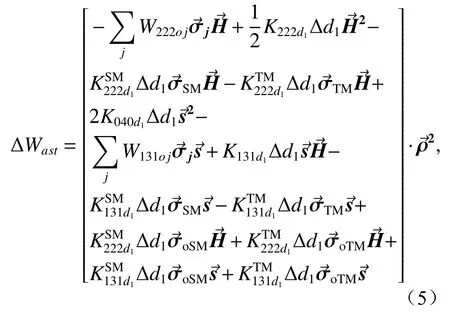
对于两类失调耦合对像散场的影响，结合解析表达式，从下面几个角度进行探讨：

3.1.1 与同轴系统比较

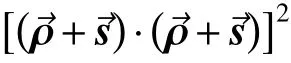
3.1.2 与两反系统比较

与文献[17]对比可知，离轴两反系统的轴向失调主要影响0°像散，而离轴三反系统不仅影响0°像散，同时影响45°像散。这是因为离轴三反系统具有更大的有效视场，轴向失调对与视场相关的波像差系数W222、W131的影响不能被忽略（而离轴两反系统在一定轴向失调范围内对W222、W131的影响可以忽略不计）。

3.1.3 与非偏轴系统比较

偏轴系统因标称状态即存在像差场偏移，故轴向失调与横向失调的耦合不仅包括像差场偏心矢量与波像差系数改变量之间的耦合，还包括波像差系数改变量与原始像差场偏轴量之间的耦合。

为了验证像散场解析表达式的指导性意义及上述结论的准确性，随机生成一组失调量（XDESM=0.01 mm、YDESM=-0.03 mm、ZDESM=0.1 mm、ADESM=-0.002°、BDESM=-0.005°、XDETM=-0.03 mm、YDETM=0.02 mm、ZDETM=-0.05 mm、ADETM=0.001°、BDETM=-0.003°），此时特定视场点像散的改变量如表3 所示。同时，也给出了不同情况下的像散场分布图，如图2 所示。表3 第3 列和第4 列数值接近，证明该解析表达式可以准确求解失调导致的不同视场点像散系数的变化量。图2 与参考文献[17]中图2 进行对比，可以验证上述部分结论。

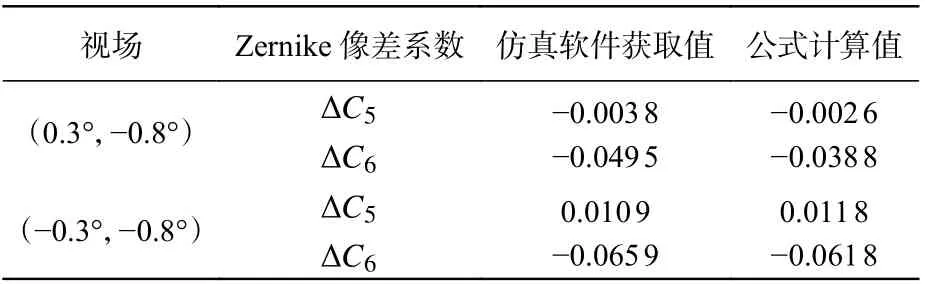
表3 不同方法获得的像散系数差值Tab.3 The difference in the astigmatism coefficient obtained by different methods (λ=632.8 nm)

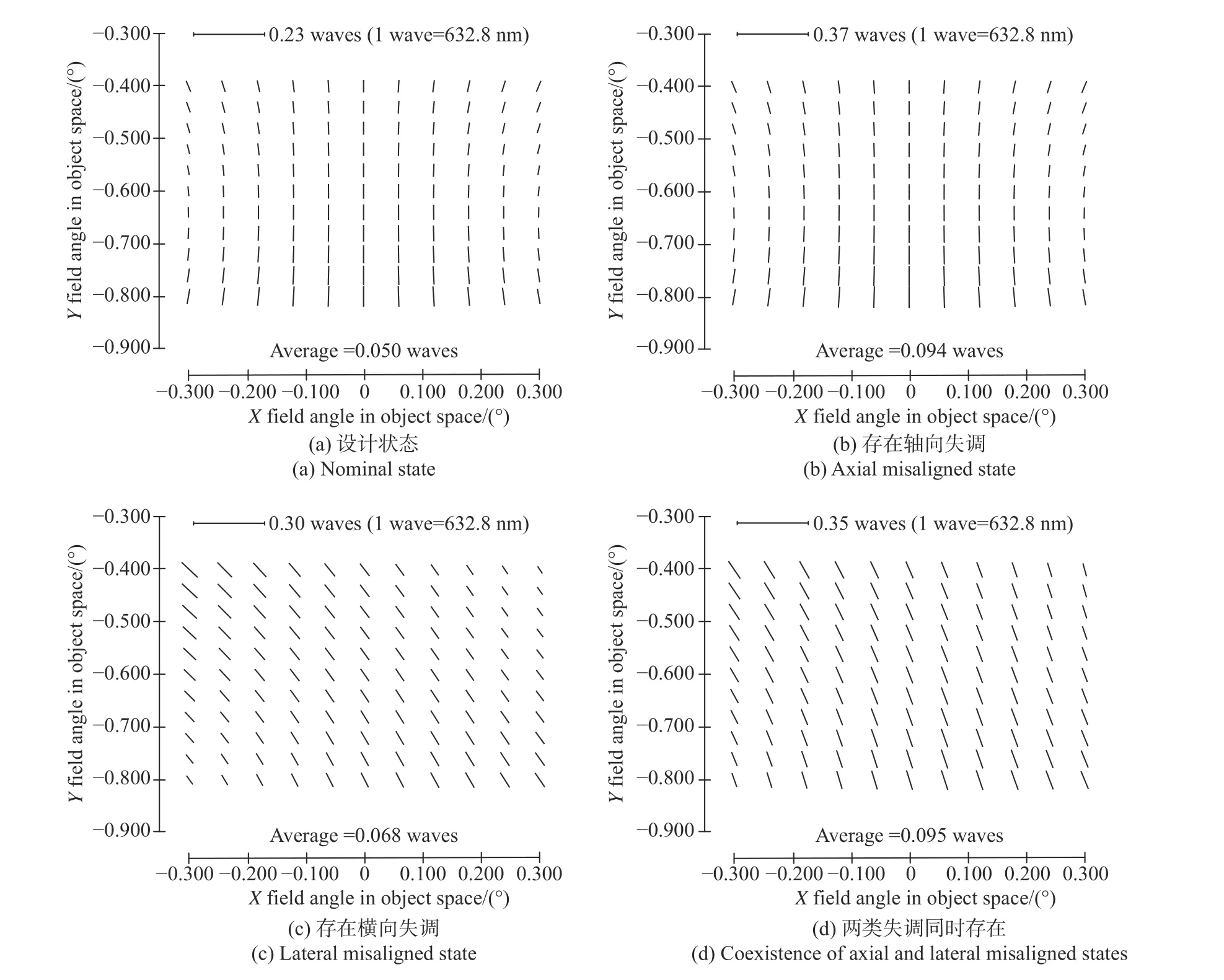
图2 不同状态下的像散场Fig. 2 FFDs (full field displays) for astigmatism in different states

3.2 两类失调耦合对彗差场的影响

由式（4）可知，当横向失调和轴向失调同时存在时，偏轴离轴三反系统彗差场增量可表示为：

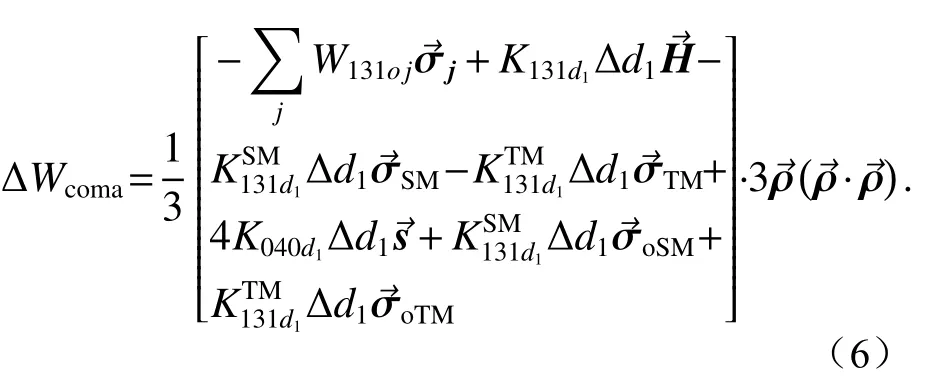
对于两类失调耦合对慧差场的影响，结合解析表达式，从下面几个角度进行探讨。

3.2.1 与同轴系统比较

由公式（3）可知，当→s为零时，关系式即为同轴系统波像差表达式。显然，ΔW040j只影响球差场分布。当不为零时，系统即为离轴系统。根据矢量乘法，ΔW040j系数对应的光瞳关系将展开出项，即衍生的彗差项，且光瞳偏心矢量对这种影响进行了放大。因此，相比于同轴系统，离轴系统在引入球差的同时，也衍生出彗差且ΔW040j衍生出的彗差是视场常量彗差。

3.2.2 与两反系统比较

与文献[17] 对比可知，离轴两反系统轴向失调主要影响90°彗差，而离轴三反系统不仅影响90°像散，同时影响0°彗差。这是因为离轴三反系统具有更大的有效视场，视场内占据主导地位的不再是W040引入的常量彗差。轴向失调对与视场相关的波像差系数W131的影响不能被忽略。

3.2.3 与非偏轴系统比较

偏轴系统因标称状态下即存在像差场偏移量，设计状态下的像差场偏心矢量与新波像差系数（轴向失调导致）相互作用，导致像差分布发生改变，进一步导致轴向失调与横向失调耦合。

为了验证彗差场解析表达式的指导性意义及上述结论的准确性，针对上一组随机失调量，确定特定视场点彗差的改变量，如表4 所示。同时，也给出了不同情况下的彗差场分布图，如图3所示。表3 中第3 列和第4 列数值差异较小，证明了慧差场解析表达式描述任意视场点彗差系数改变量的准确性。图3 为与参考文献[17]中图3的对比结果，其可以证明上述部分结论的准确性。

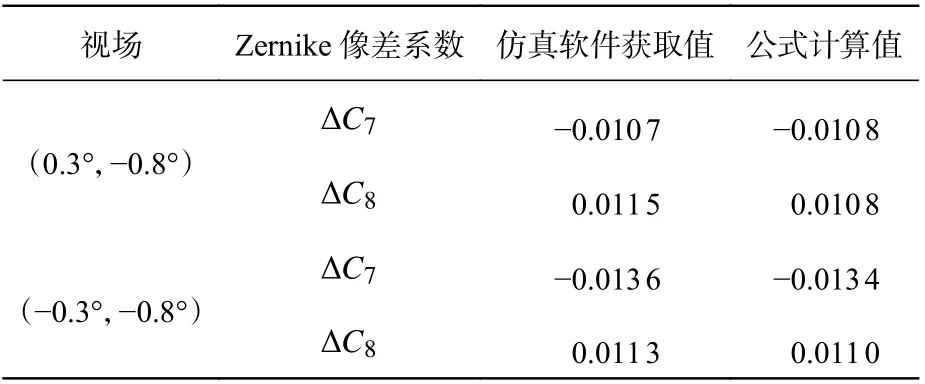
表4 不同方法获得的彗差系数差值Tab.4 The difference in the coma coefficient obtained by different methods(λ=632.8nm)

图3 不同状态下的彗差场Fig. 3 FFDs for the coma in different states

4 像差场补偿关系

针对大口径望远系统，无论是地面装调还是在轨调整，通常采用测量不同视场的波前像差（如Fringe Zernike 系数）的方法来调整光学系统[20]。上一章从内在机理层面揭示了不同失调量对像差场（波前像差）影响的耦合特性，本章将针对单一横向失调量与轴向失调量的耦合关系展开深入的研究，揭示不同失调量对像差场影响的补偿关系，这对校正系统成像质量具有重要意义。

为了近一步分析横向失调与轴向失调之间的补偿关系，本节将简化像散、彗差与不同失调量之间的解析关系。根据矢量像差理论，由式（5）、式（6）及像差场偏心矢量表达式可知，由失调引起的波像差（各主要像差系数）净改变量在视场中呈现线性分布，线性成分之外的高阶量可以忽略不计，所以，波像差系数增量可以进一步整理为：

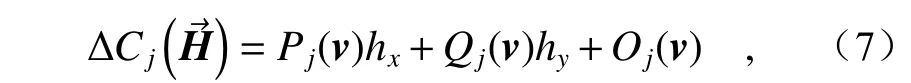
其中： ΔCj为视场坐标=(hx,hy)处由失调引起的第j项像差系数（j取5，6，7，8，分别表示0°像散、45°像散、0°彗差和90°彗差）改变量，v表示失调量向量，包含横向失调和轴向失调，Pj，Qj以 及Oj为相应的线性比例系数，它们都是失调量向量v的线性函数。Pj，Qj以 及Oj可由式（5）和式（6）进行计算，也可以通过光学软件进行计算。进而，通过式（7）可以计算（0.3°，-0.8°）视场对不同失调量的敏感度，如表5 所示。

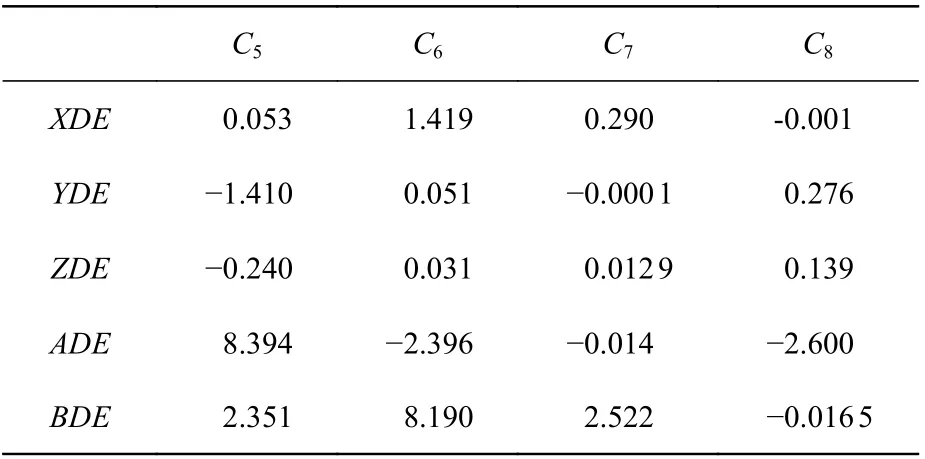
表5 像差系数对失调量的敏感度Tab.5 Sensitivity of the aberration coefficient to misalignment(632.8nm/mm and 632.8nm/°)

4.1 轴向失调补偿横向失调

横向失调存在8 个自由度，即次镜和三镜关于x轴和y轴的偏心和倾斜，而轴向失调只有一个自由度即次镜沿z轴移动，理论和实践均可证明：主动调整次镜的轴向距离不具备完全补偿横向失调的能力[11]。本小节主要揭示在调整过程中，轴向失调量和部分横向失调量之间的补偿关系。

Thompson 早期研究成果表明次镜沿x轴方向偏心与次镜绕y轴倾斜、次镜沿y轴方向偏心与次镜绕x轴倾斜对像差场的作用机理一致[21]。张晓彬[1]等的研究成果揭示出在一定范围内三镜横向失调与次镜横向失调具有明确的补偿关系，即三镜横向失调对部分像差场的影响可以等效转化为次镜横向失调对部分像差场的影响。此处为揭示补偿像散场后彗差场的变换情况及补偿彗差场后像散场的变换情况，选取次镜偏心失调引入的像差与轴向失调引入的像差之间产生的补偿关系进行分析。

通过式（7）可以得出：在一定失调范围内，像散场的耦合主要源自次镜轴向失调与次镜沿y轴方向偏心产生的 0°像散；彗差场耦合主要源自次镜轴向失调与次镜沿y轴方向偏心产生的90°彗差。与离轴两反系统不同的是，在补偿的过程中二者引入的45°像散和0°彗差不再能直接被忽略。表5 可以证明上述结论。

4.1.1 优先补偿像散场时对彗差场的影响

当以像散场最小为调整目标时，解析关系为：

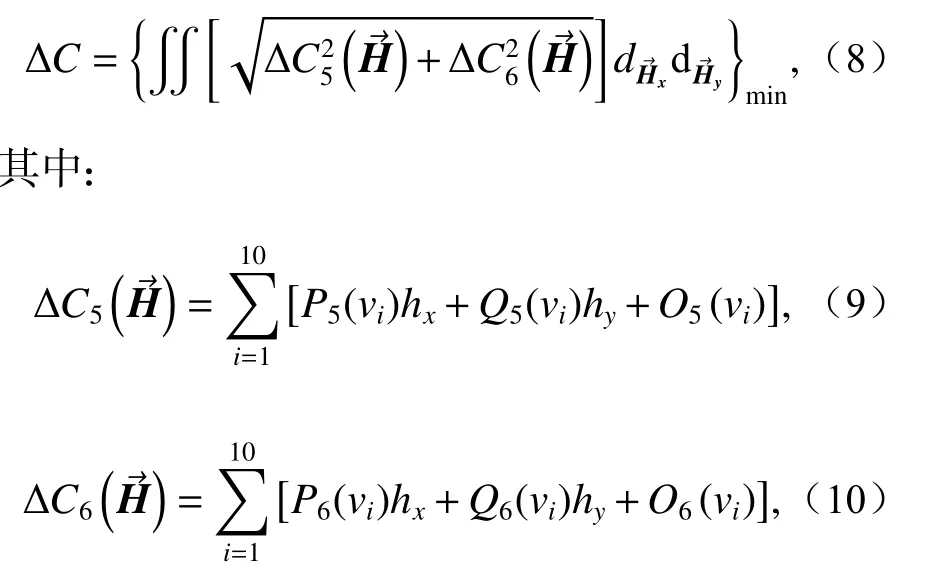
式中：vi指的是次镜轴向失调与次镜沿y轴方向的偏心。

为更直观地揭示以像散场改变量最小为目标进行轴向失调补偿横向失调时像散场与彗差场的分布情况，随机选取横向失调YDESM=0.1 mm 为例进行说明，通过式（8）可计算轴向补偿量，为ZDESM=-0.32 mm，补偿前后像散场、彗差场分布如图5 所示（失调和补偿引入的像面倾斜和离焦可以通过摆镜进行调整，分析时不做考虑）。

图5 以彗差场改变量最小为目标进行补偿时像差场分布Fig. 5 Aberration field distribution when the minimized coma field change is set as the goal for compensation

比较图4（b）和图2（a）可以发现：在一定范围内，通过调整轴向间距引入像散可以在一定程度上补偿轴向失调引入的像散，且主要补偿的是0°像散（与光瞳偏心矢量相关）。同时可以发现在补偿像散时，彗差场分布偏离设计状态。

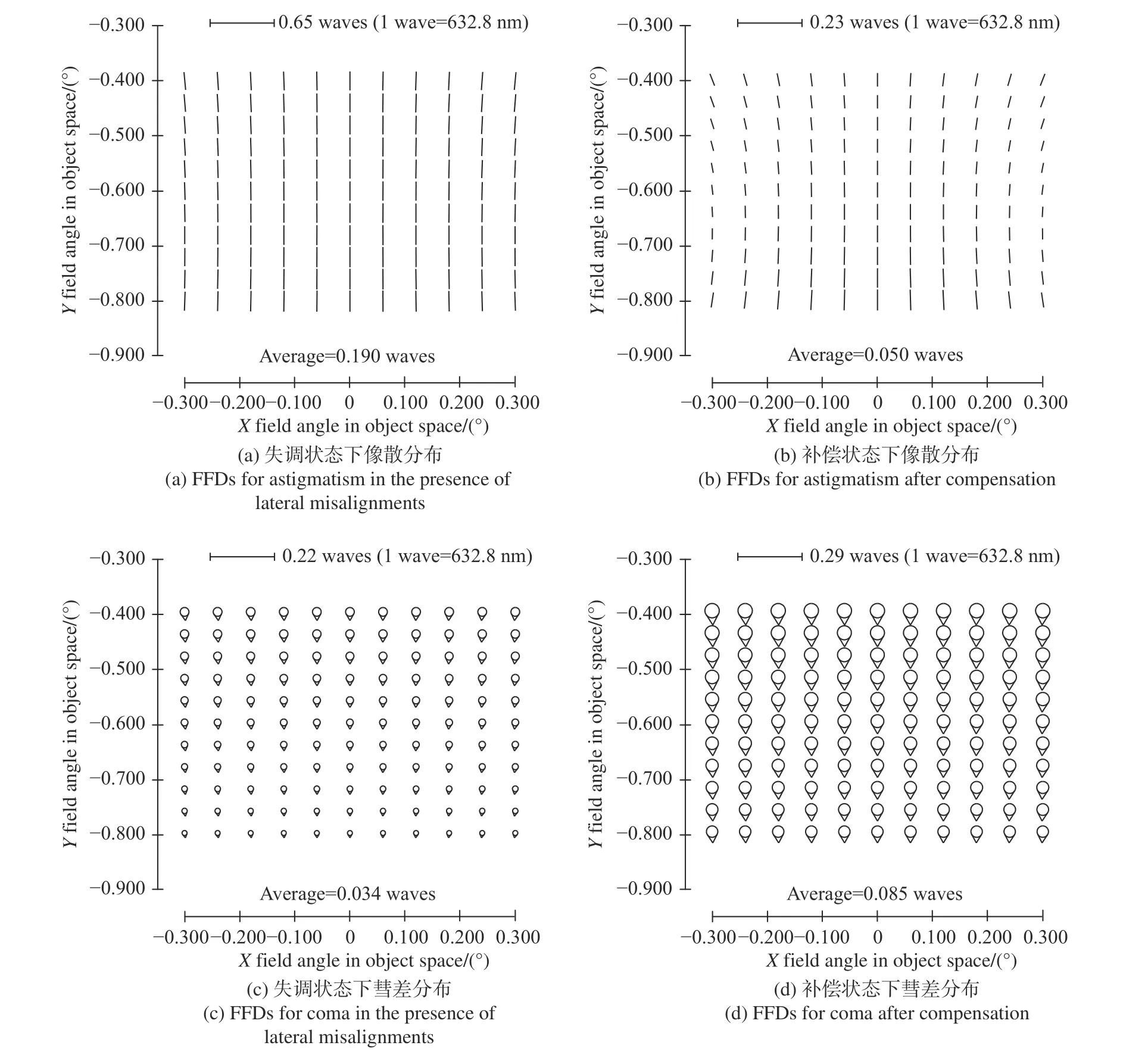
图4 以像散场改变量最小为目标进行补偿时像差场分布Fig. 4 Aberration field distribution when the minimized astigmatism field change is set as the goal for compensation

4.1.2 优先补偿彗差场时对像散场的影响

当以彗差场最小为调整目标时，解析关系为：

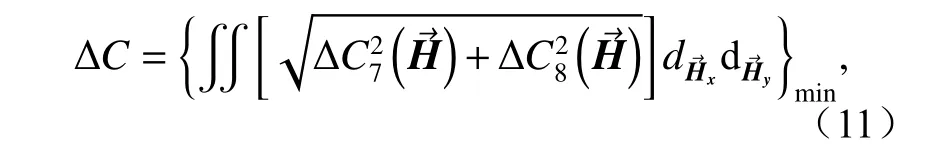
其中：

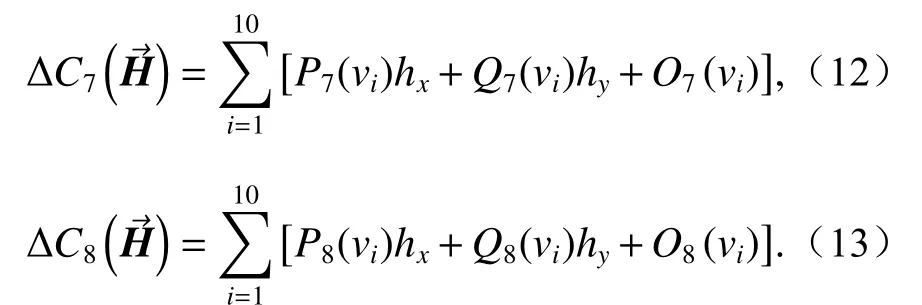
为了分析优先补偿彗差场对系统像差场的影响，同样以横向失调YDESM=0.1 mm 为例进行说明，通过式（11）可计算轴向补偿量，为ZDESM=-0.16 mm，补偿前后像散场、彗差场分布如图5所示。

比较图5（a）、图4（c）和图3（a）可以发现，在一定失调范围内，通过主动调整轴向距离可以使彗差场分布趋向于设计状态。比较图5（b）、图4（a）和图2（a），可以发现补偿彗差场时像散场同时减小，但没有补偿至设计状态。

对比图4 和图5 及对比求解的轴向调整值，可以得出：优先补偿像散时，彗差将偏离设计状态。优先补偿彗差时，像散将得不到有效的补偿，这与两反系统轴向失调补偿横向失调具有相似性，然而，同时可以证明离轴三反补偿与离轴两反补偿具有一定差异：根本原因为离轴三反视场更大，轴向失调引入的不再仅仅是常量像散。

为了更加全面地评价补偿过程中对光学系统像质的影响，本文给出不同状态下的RMS 波前像差分布（注：从CodeV 软件读取的RMS 波前误差没有去除离焦及倾斜，故全视场RMS 波前误差因折转镜位姿的不同略有不同），如图6 所示。从图6 可以看出：无论优先补偿像散场还是彗差场，系统RMS 波前误差都会降低，但优先补偿像散场，系统具有更好的像质。这与解析理论的推导结果是一致的。基于此，可以得出一个对系统调整有价值的结论，即系统在装调阶段出现一类像差场接近设计状态，而另一类像差场偏离设计状态，那么两类失调可能处于补偿状态，可以微小调整轴向间距后再次调整横向失调，观察系统像差场变化规律，进而完成系统装调。

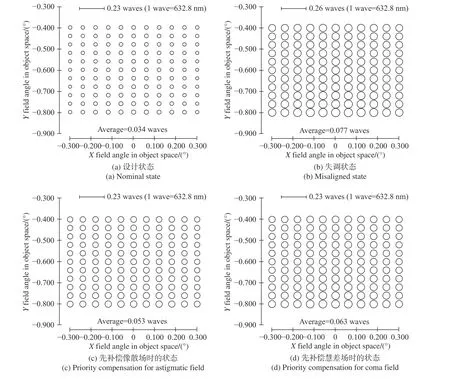
图6 利用轴向自由度补偿横向失调过程中不同状态全视场波前误差RMS 分布Fig. 6 Full-field distributions of RMS wavefront error for different states in the process of compensating the aberrations induced by lateral misalignments using axial mialignments

4.2 横向失调补偿轴向失调

系统RMS 波前误差与不同类型像差之间具有如下关系：

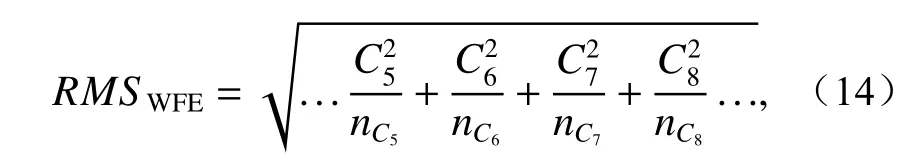
其中：nCj代表不同类型像差系数对RMS 波前误差的权重因子。

空间望远镜通常配备摆镜进行调整像面倾斜和调焦，需要注意的是，如果空间望远镜在轨像差场存在一定离焦时，不太容易判断出其是由次镜失调产生的还是由摆镜失调产生的。因此，在不考虑离焦及高阶像差时，在轨横向失调补偿轴向失调的目标函数可以表示为：

其中：v依次取次镜的5 个失调量，包括轴向失调和横向失调。

当式（15）取最小值时，系统处于最佳的补偿状态，为了验证横向失调补偿轴向失调的可行性及上述目标函数的可靠性，随机选取次镜轴向失调ZDESM=1 mm 进行验证。通过式（15）可计算横向调整量为：YDESM=-0.054 8 mm；ADESM=0.036 8°（这里必须说明，通过4.20 式求取的次镜横向位姿补偿调整量并不是唯一的，与选取的优化算法及优化算法极值点相关。该实例可以证明通过主动调整横向位姿，可以有效补偿轴向失调对像差场的影响）。补偿前后的像差场、彗差场分布如图7 所示，补偿前后的RMS 波前误差分布如图8 所示。比较图7（a）和图2（a）可以发现，像散场均值接近设计状态，但全视场像散场分布形式发生了改变，边缘视场45°像散成为主要像差成分。比较图7（b）和图3（a）可以发现，彗差场分布同样偏离设计状态，彗差方向已经发生改变。但比较图8（b）和图6（a）可以看出RMS 波前误差分布接近设计状态。

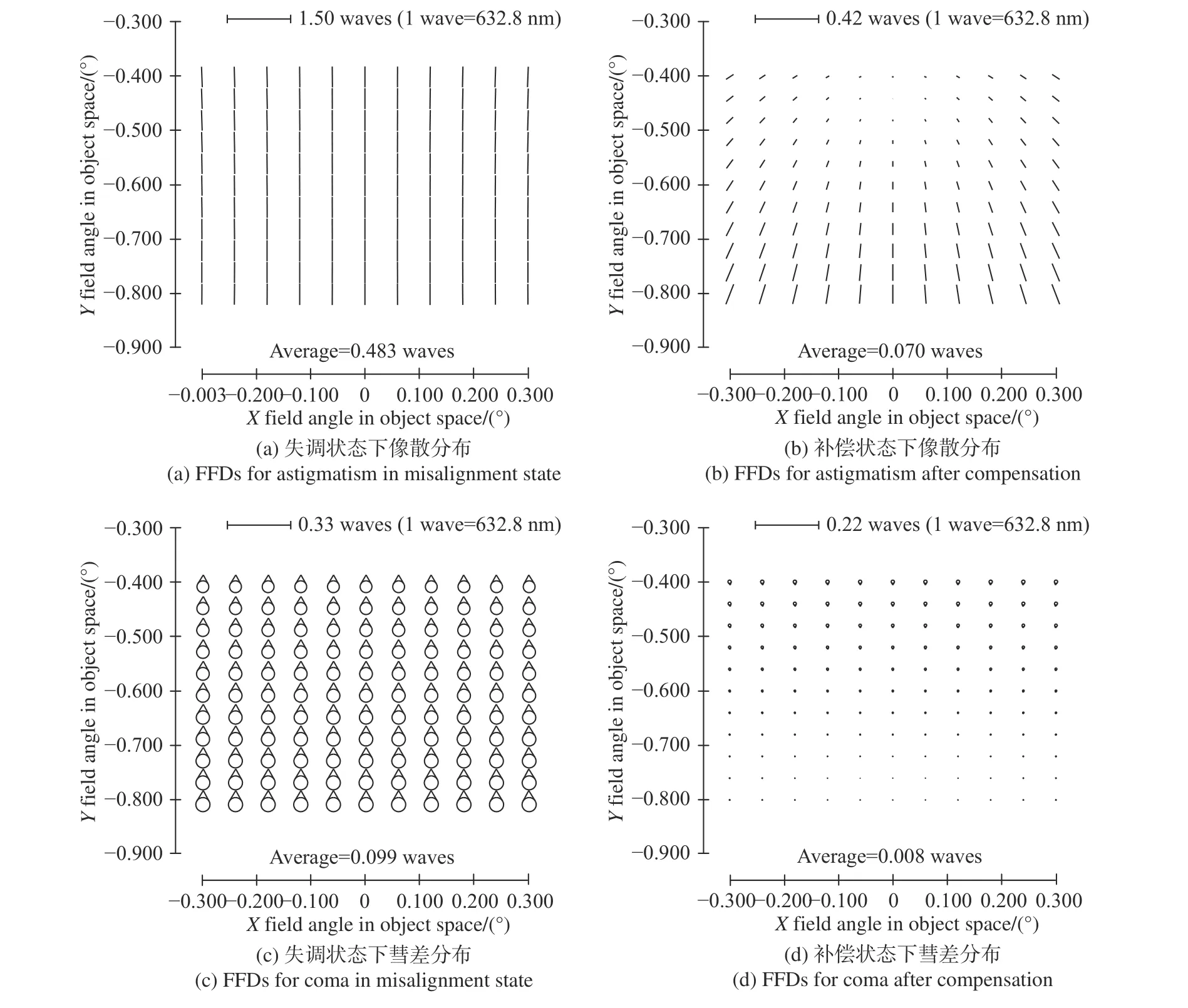
图7 横向失调补偿轴向失调时不同阶段像差场分布Fig. 7 Aberration field distribution in different states when the lateral misalignment compensates for the axial misalignment

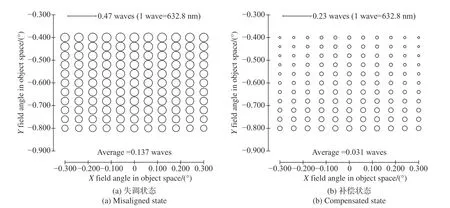
图8 利用横向位姿自由度补偿轴向失调（ZDE_SM=1mm）前后全视场RMS 分布Fig. 8 Full-field distributions of RMS wavefront error before and after compensating the aberrations induced by axial misalignments (ZDE_SM=1mm) using lateral mialignments

轴向失调只有正负两个方向，同时随机选取次镜轴向失调ZDESM=-1 mm 进行验证，校正前后RMS 波前误差分布如图9 所示。比较图9（b）和图6（a）可以看出RMS 波前误差分布接近设计状态，但补偿后系统平均RMS 波前误差略高于设计状态。

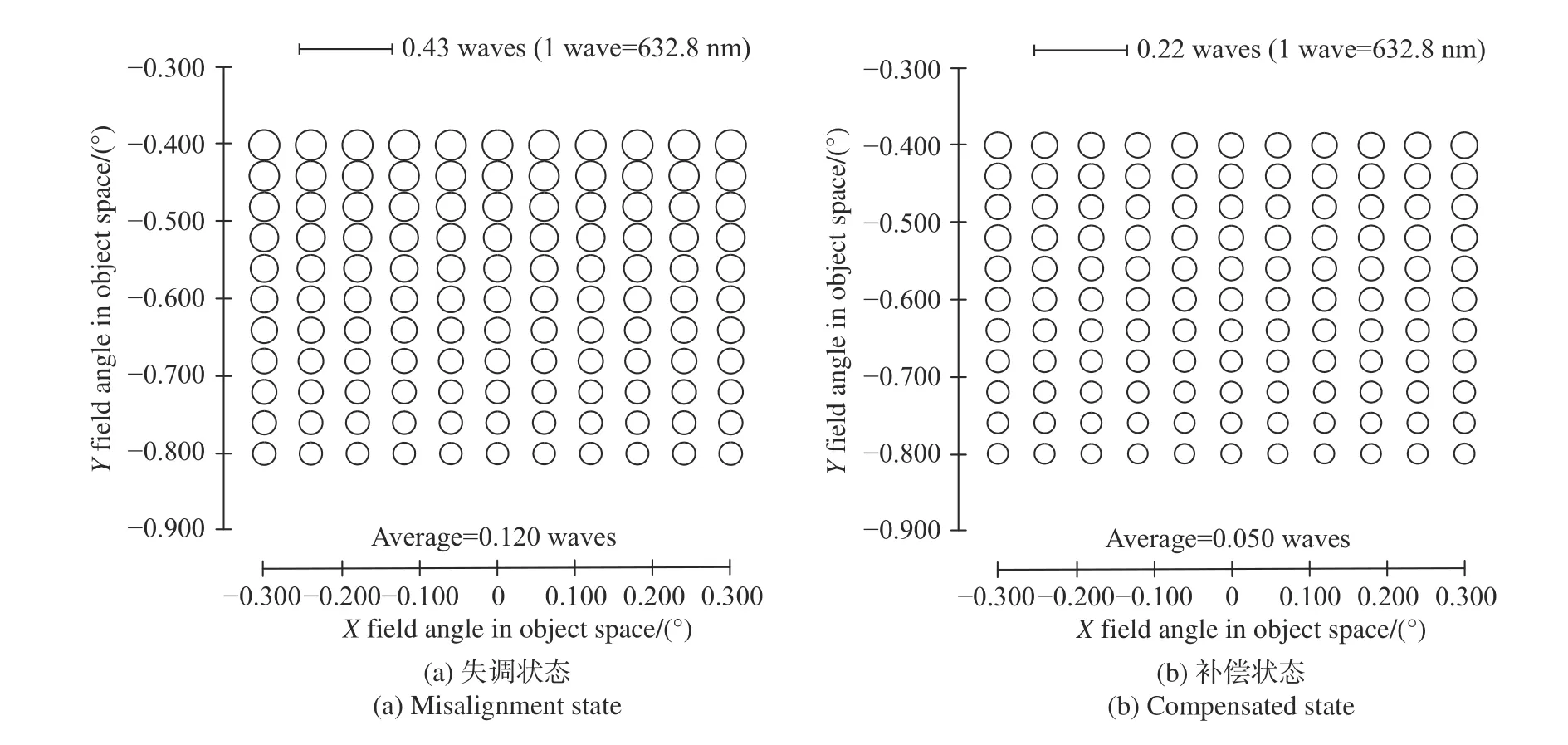
图9 用横向位姿自由度补偿轴向失调（ZDE_SM=-1mm）前后全视场RMS 分布Fig. 9 Full-field distributions of RMS wavefront error before and after compensating the aberrations induced by axial misalignments (ZDE_SM=-1mm) using lateral misalignments

离轴两反横向失调补偿轴向失调可以使像散场、彗差场分布形式接近设计状态[17]，但离轴三反补偿后可以降低系统有效视场内像散、彗差的平均值，不能恢复到设计状态，这可由式（4）给出原因，即轴向失调导致的与视场相关的像差系数的改变对系统像差场的影响不能被忽略。

5 实验验证

为了验证离轴三反轴向与横向失调量像差耦合解析表式的准确性，及横向失调补偿轴向失调可行性，本文以实验室现有系统为例进行实验验证，实验原理及实际光路图如图1 所示（因干涉仪测量受振动、气流等多种因素影响，本结果为外界干扰小的情况下获得的）。该光路主要由平面反射镜、离轴三反系统、4D 干涉仪和相关辅助机械及电子设备组成。具体实验流程如下：

（1）完成系统装调，用干涉仪测量中心视场波前像差并记录，测量结果如图10（a）（彩图见期刊电子版）所示。

（2）通过六轴平台调整次镜，使次镜产生一定的轴向失调（为同时验证仿真的可靠性，失调量依然为1 mm），然后通过六轴平台合理调整摆镜，用干涉仪测量与步骤（1）对应的中心视场的波前像差并记录，测量结果如图10（b）（彩图见期刊电子版）所示。

（3）通过式（14）计算次镜横向调整量，为YDESM=-0.054 8 mm;ADESM=0.036 8°；

（4）将步骤（3）计算的调整量输入到六轴平台，调整次镜到预定位置并通过六轴平台合理调整摆镜位置；

（5）用干涉仪测量中心视场波前像差并评价补偿效果，测量结果如图10（c）（彩图见期刊电子版）所示。

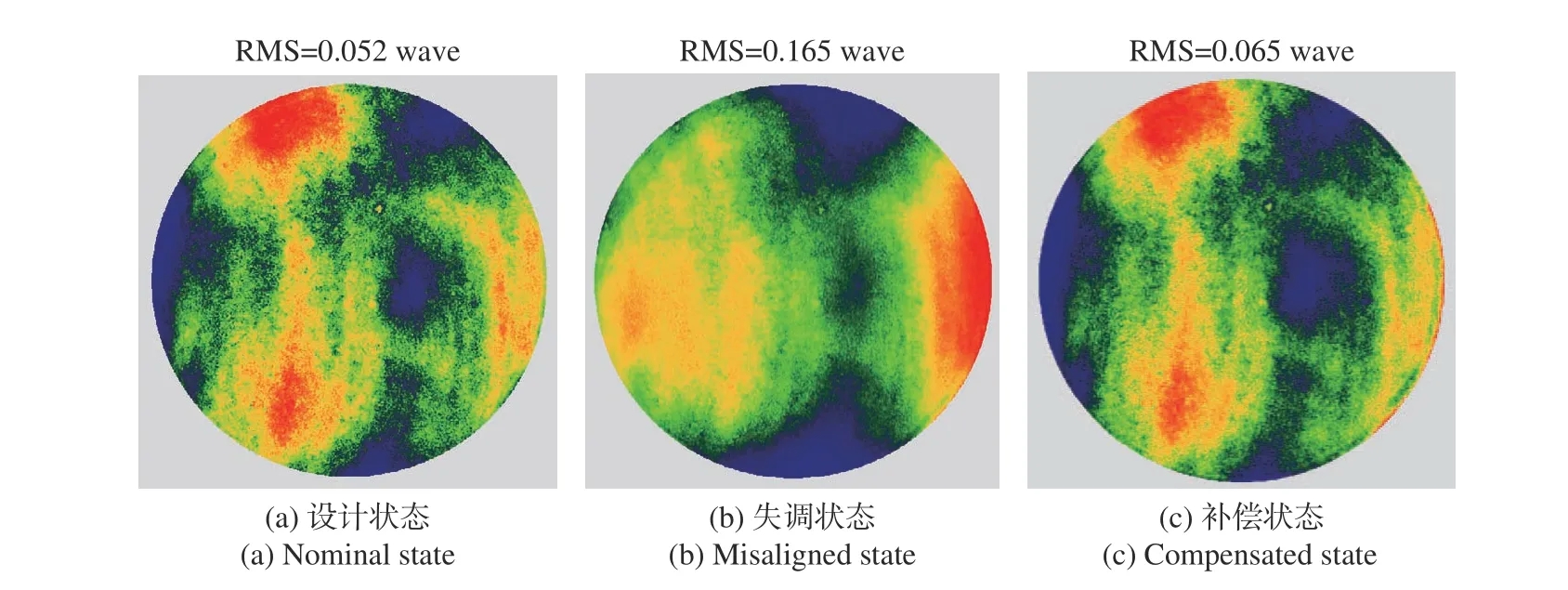
图10 不同状态下干涉仪测量结果（去除部分高频量）Fig. 10 Measurement results with interferometer under different conditions (remove some high frequency)

比较图10（c）和图10（b）可以得出：在一定范围内，横向失调对轴向失调具有良好的补偿效果，比较图10（c）和图10（a）可以看出，RMS 波前误差改变量小于0.02λ，该补偿策略具有实际应用价值。

6 结 论

本文根据离轴三反系统轴向失调与横向失调像差场耦合解析关系，分析了轴向失调与横向失调对像散场、彗差场影响的耦合特性，揭示了两者耦合导致系统装调或在轨调整波前像差处于局部极值的内在机理，提出了主动调整次镜横向位姿补偿轴向失调引入的像散、彗差的在轨调整策略（横向失调引入的离焦不能补偿轴向失调引入的离焦）。通过仿真及实验结果可以发现：在一定范围内，通过调整次镜横向位姿可以补偿次镜轴向失调对像差场的影响（忽略离焦）。由实验系统可看出，当轴向失调误差在±1 mm 范围时，RMS 波前误差改变量小于0.02λ。同时，也可以得出：当离焦较小时，望远镜在轨因失调导致像质退化时，可优先调整次镜横向位姿进行校正。