LightGBM模型及其应用
舒仕文
(贵州财经大学 贵州 贵阳 550025)
0 引言
GBDT(梯度提升决策树)是可用于回归预测,也可用于分类(提前规定一个阈值,如果计算出的值大于阈值,则设置为正例;如果计算出的值小于阈值,则设置为负例)的集成监督学习算法。该集成算法有3个优点,分别是提升、梯度和决策树:提升是把多个弱分类器组合起来;梯度是在提升过程中提高损失函数的灵活性和便利性的算法;决策树是算法使用CART决策树为基础弱分类器[1]。
实现传统的GBDT需要扫描所有数据实例的每个特征。因此,特征和实例的数量越多,其计算就越复杂。所以在处理大数据时,传统的GBDT非常耗时。
解决耗时问题的一个方法是减少数据或特征的数量,但不知如何从GBDT中采样数据。虽然有一些方法可以基于权值对数据进行采样,以加快数据的训练过程,但GBDT中没有样本权值[2],这些方法不能直接应用于GBDT。因此,针对该问题提出了两种算法:GOSS算法(梯度单边采样)和EFB算法(互斥特征捆绑)。将加入GOSS和EFB两种算法的GBDT称为LightGBM。
1 LightGBM
1.1 单边梯度抽样算法
由于GBDT没有权值,所以根据抽样点权重的数据采样方法不能直接应用于GBDT,但其可以利用每个数据实例的梯度来进行采样数据。基于此,GOSS算法保留所有梯度较大的数据实例,然后随机采样所有梯度较小的数据实例。GOSS算法在梯度较小的数据实例中引入一个固定乘数,用于计算信息增量,目的是减少该方法对数据分布的影响[3]。步骤如下:GOSS首先根据数据实例梯度的绝对值对数据实例进行排序,然后选择最佳的a×100%的实例,接着从剩下的数据中随机选择前面b×100%的实例。最后GOSS通过将采样数据按较小梯度的数据乘以(1-a)/b来计算信息增益。其中a,b∈(0,1),a表示大梯度数据的采样率,b表示小梯度数据的采样率。
1.2 互斥特征捆绑(EFB)
高维数据通常非常分散。正是由于这种分散性,才有可能不损失地减少特征空间中的特征数量。在一个特征分散的空间里,许多特征是相互排斥的,所以这些互斥的特征可以捆绑成一个单独的特征(称为互斥特征包)。使用特征扫描算法,可以用与单个特征相同的包构造特征的直方图。这种方法可以将构造直方图的复杂度从数据实例数量n×特征数量j变为数据实例数量n×特征捆绑数量j′,当捆绑的特征数量远远小于原始特征数量时,可以显著提高GBDT的训练速度而不影响其准确性。
EFB算法将许多互斥特征捆绑到低维密集特征上,可以有效避免不必要的零特征值计算。事实上,如果将每个非零特征的数据记录在一个表中,也可以优化基于基本直方图的算法,从而忽略零特征值。通过扫描该表中的数据,构造直方图的代价将从原始数据变为非零特征的数。但是这种方法需要额外的内存和计算成本,以便能够在整个树的增长过程中维护这些特征表。
1.3 直方图算法
在直方图算法中,连续浮点特征值会被离散为k个整数,同时构造一个直方图,其宽度为k。当在数据中遍历时,统计数据会根据离散值作为索引收集在直方图中。数据经过一次遍历后,直方图会收集所需的统计信息,然后根据直方图的离散值进行遍历,以找到最佳分割点。XGBoost需要遍历所有离散值,而LightGBM仅遍历k个值。
1.4 理论分析
从输入空间xs到梯度空间g,GBDT通过决策树学习一个函数。假设有n个实例训练数据集{x1,x2,…,xn},其中xi是输入空间xs中维度为s的向量,在模型的每次迭代中,损失函数的负梯度相对于模型的输出表示为{g1,g2,…,gn}。决策树模型以最大的信息增益分割每个节点。对于GBDT,信息增益用分裂后的方差来度量[4],定义如下:
在决策树的固定节点上定义训练数据集O。该节点在点d处分裂,特征j的方差增益定义为公式(1):
其中no=∑I[xi∈O],njl|o(d)= ∑I[xi∈ O:xij≤d]和nj|lo(d)= ∑I[xi∈ O:xij> d]。
对于特征jj,算法中dj*=argmaxdVj(d),并且计算出Vj(dj*)为点dj*处的最大增益。然后根据dj*点的特征j*将数据划分为左右两个子节点,见图1。
如图2,XGBoost使用按层生长的增长策略,通过一次遍历数据,可以同时分离相同的叶子层,从而更容易针对多个线程进行优化,并能很好地控制模型的复杂性,但这种算法很低效。与XGBoost不同,LightGBM使用按叶子生长的策略,即在所有当前叶子中搜索出分裂增益最大的叶子,然后对其进行分裂,一直重复此过程。与按层生长的增长策略方法相比,按叶子生长方法的优势在于,在相同的分裂次数下,叶子生长方法减少了误差,提高了精度;但其缺点是它可能会创建出更深层次的树,容易出现过拟合。所以LightGBM在按叶子生长方法上创建一个最大深度限制,目的是确保模型的高性能和防止过拟合。
在GOSS算法中,首先根据训练实例的梯度绝对值对训练实例进行降序排序;其次,梯度较大的前a×100%的实例用子集A表示;然后用Ac表示由(1-a)×100%具有较小梯度的实例组成的集合,进一步用B表示随机采样大小为b×|Ac|的集合。最后根据集合A∪B上的估计方差的增益VJ~(d)拆分实例,即公式(2):
其中Al={xi∈A:xij≤d},Ar={xi∈A:xij>d},Bl={xi∈B:xij≤d},Br={xi∈B:xij>d},并且Ac的大小与集合B上的梯度总和乘以(1-a)/b相等。因此,GOSS算法中,在较小的实例子集上不是使用精确值Vj(d)确定分割点,而是使用估计的V~J(d)来确定,这样可以显著降低计算成本。
2 实例分析
2.1 数据来源及描述
本文中使用的3个二分类数据集皆由UCI数据库收集,从Kaggle下载。随机选取3个数据集的75%做训练集,25%做测试集。其中电信客户流失数据集属于类别不平衡数据,本文使用SMOTE采样方法对其进行上采样处理。SMOTE是一种具有代表性的过采样方法算法,即把少量样本的样本进行采样,它是基于随机过采样算法的改进。由于随机过采样技术是一种简单地复制样本以增加多个样本的策略,因此很容易产生模型过拟合的问题,即能使模型学习获得的信息过于特殊而不够泛化。SMOTE算法的基本思想是分析少数样本,根据少数样本以KNN技术合成新样本,并将其添加到数据集中,流程见图3。
采样前电信客户流失数据集的正例和反例的比例约为1∶3,使用SMOTE算法采样后电信客户流失数据集的正例和反例的比例为1∶1。处理后的具体数据集的信息见表1。
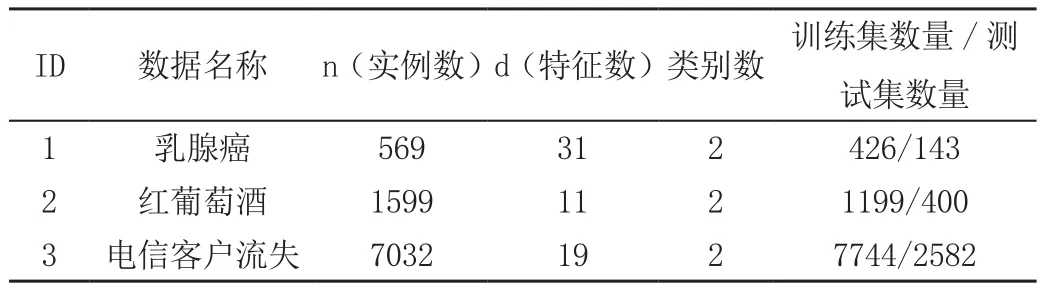
表1 数据集信息
红葡萄酒数据集、电信客户流失数据集的全部特征描述见表2、表3。
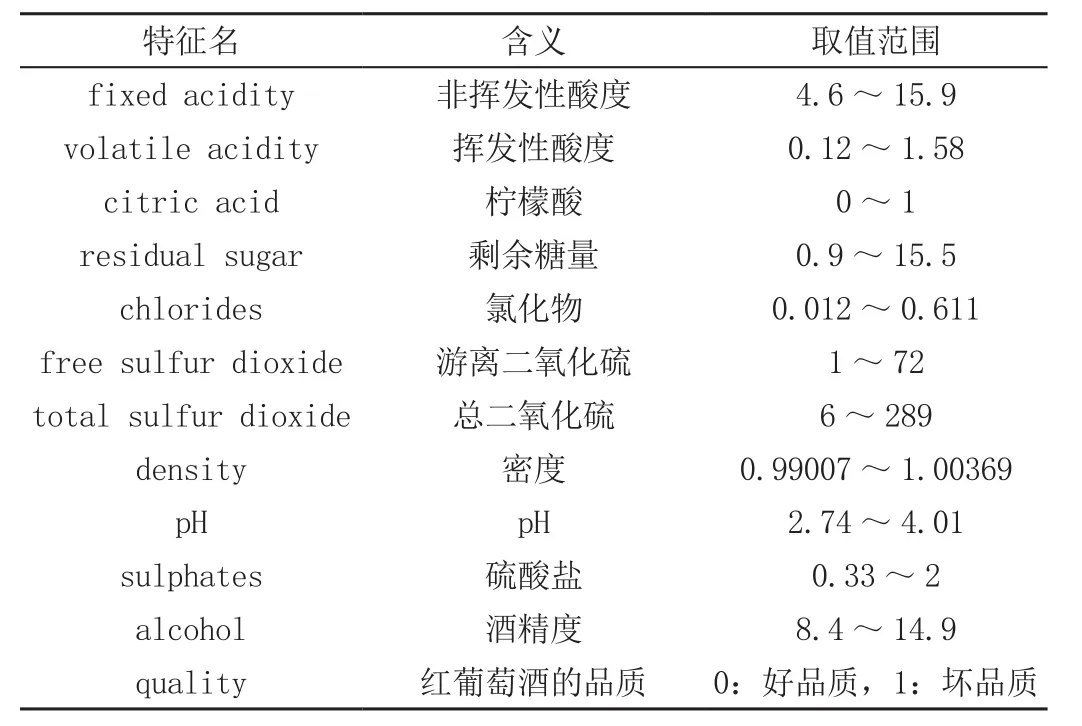
表2 红葡萄酒数据特征描述

表3 电信客户流失数据特征描述
乳腺癌数据集包含30个特征,前10个特征表示细胞核特征的平均值;第11至第20个特征表示细胞核特征值的标准差,反映不同细胞核在各个特征数值上的波动情况;第21到30个特征为样本图像中细胞核特征值的最大值。
在3个数据集实例中,红葡萄酒数据集和乳腺癌数据集的特征是定量变量,电信用户流失数据集中有定量变量(如每月费用),也有定性变量(如性别)。
2.2 模型评估
建模过程中的一个重要步骤是建立科学且合理的数据指标,以评估算法模型的预测性能。因此,本文使用Accuracy、Recall、Precision、F1-Score以及AUC值作为模型的评估指标,机器学习中较常用的评估性能的是混淆矩阵,见表4,它能够把预测分布结果直观地显示[5]。各个指标的计算方法如下。

表4 混淆矩阵表
准确率(Accuracy):
Accuracy=(TP+TN)/(TP+FP+TN+FN)
准确率指被模型分类正确数占总样本实例数量的比例。
召回率(Recall):
Recall=TP/(TP+FN)
召回率描述了实际为正的样本中被预测为正样本的比例。
精确率(Precision):
Precision=TP/(TP+FP)
精确率描述了正确预测为正的占全部预测为正的比例。
F1值(F1-Score):
F1=(2TP)/(2TP+FP+TN)
F1分数是调和精确率和召回率的平均数。
2.3 ROC曲线和AUC值
为了量化模型分析,引入AUC的概念,即ROC曲线下面积,ROC曲线一般都会在直线y=x的上方,AUC值指从实际值为1的样本内预测成功的概率大于实际值为0的样本内预测失败的概率,AUC值一般介于0.5~1。AUC值越高,模型的预测性能越好。
3 试验环境
本文试验是在Python 3.7.3 [MSC v.1915 64 bit(AMD64)]:: Anaconda,Inc.on win32环境,在Python自带的scikit-learn接口下进行。
4 LightGBM模型运行结果
如表5所示,LightGBM模型在对乳腺癌、红葡萄酒、电信客户流失3个数据集的分类预测中,准确率、召回率、精确率、F1-score均在0.8以上,且AUC值分别为0.99、0.88、0.92。从以上模型评估指标的结果说明,LightGBM模型的分类预测效果较好。且LightGBM模型相对于AdaBoost、GBDT和XGBoost的运行时长和所占用的内存均有很大的提升,特别是在对电信客户流失的应用中,更突出LightGBM在数据量大的数据集中的计算优势,见表6。
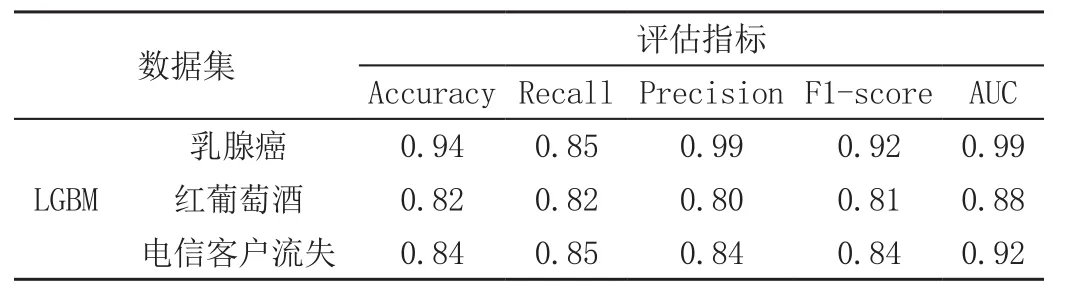
表5 LightGBM模型评估指标
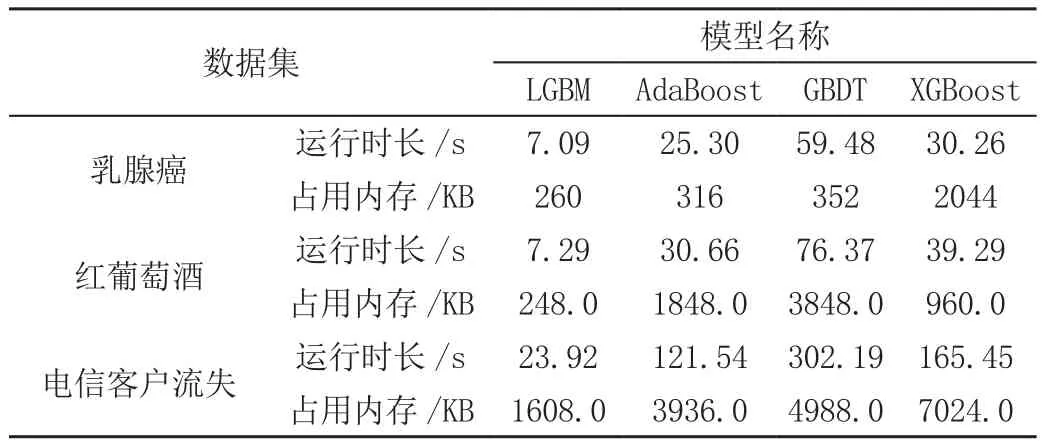
表6 各模型运行时长和占用内存
5 LightGBM模型的优缺点
5.1 优点
(1)计算速度更快。LightGBM使用直方图算法将样本转换为组间复杂度直方图,并使用单边梯度算法在训练期间过滤掉具有较小梯度的样本,从而减少计算量;LightGBM采用优化后的特征并行、数据并行方法,甚至当数据量非常大时采用投票并行的策略以加速计算,同时也会优化缓存。
(2)占用内存更小。LightGBM 使用直方图算法将存储特征值转变为存储箱值,并且采用捆绑相互排斥的特征来减少训练前的特征数量,从而减少内存使用量。
(3)支持类别特征(即不需要做独热编码)。大多数机器学习方法不能直接支持类别功能。通常情况下,类别的属性需要转换为多维的独热编码,但这会降低空间和时间的效率,使用类别在实践中非常常见。在此基础上,LightGBM优化了类别的处理,即类别功能可直接输入,无需额外的独热编码扩展,并将类别特征的决策规则添加到决策树算法中。
5.2 缺点
可能会创建比较深的树从而易发生过拟合;LightGBM是基于偏差的算法,因此,它将对噪声点更敏感;对最优解的搜寻是基于最优变量的切分,没有考虑当最优解可能是所有特征的组合时这一事实。
6 结语
本文提出了LightGBM模型,介绍了GOSS算法、EFB算法和直方图算法。然后通过实例分析LightGBM在二分类数据中的应用,计算出模型评估指标的值,并归纳出其优点和缺点,以供参考。

