利用排列小波熵评价脑电信号中的爆发抑制水平

袁思念，但果，3，叶继伦，3，张旭，3，牛航舵，马胜才，李若薇，朱子孚

1.深圳大学医学部生物医学工程系，广东深圳 518060；2.深圳市生物医学工程重点实验室，广东深圳 518060；3.广东省生物医学信号检测与超声成像重点实验室，广东深圳 518060

前言

脑电（Electroencephalogram,EEG）信号的爆发抑制信号是一种特殊的异常脑电波形，其特征表现为高幅高频的爆发状态和低幅值的抑制状态交替出现，并且这种交替变化没有周期性［1］。爆发抑制信号常出现在深度麻醉状态，在麻醉深度监测中，评价爆发抑制水平具有非常重要的意义［2］。随着麻醉深度的加深，EEG 的抑制状态在时间上增加，当长时间处于抑制状态，会导致脑受损或脑死亡［3］，因此，在麻醉过程中，爆发抑制模式的出现可以看作药物控制的一个关键点，是评价麻醉深度的一个关键指标［4］。

EEG 信号爆发抑制水平的评价主要是利用爆发抑制比（Burst Suppression Ratio, SR）指标来量化［5］，该指标的定义最早由Rampil 公布［2］，将幅值不超过5 μV、持续时间大于0.5 s的脑电信号，判定为抑制信号段，在1 min 内计算抑制信号段占总时间段的比值，为爆发抑制比，爆发抑制比数值越高，代表信号抑制水平越强。

目前市场上主流的麻醉深度监测器均给出了评价爆发抑制水平的参数［6］，虽然各自的计算方法不同，但都是通过对信号进行预处理后，使用算法检测一段时间内的抑制水平段，最后将抑制水平段占总时间段的比值来量化爆发抑制水平，如双谱指数（Bispectral Index,BIS）监护仪使用Rampil 公布的SR指标［7-8］，熵模块中的算法则使用非线性能量因子来检测爆发抑制［9-10］。这些方法均是基于信号的幅度特征，通过阈值方式检测信号中的抑制水平段，而爆发抑制波形具有不平稳，非线性等特征，使用阈值的方式容易造成对信号的误判，因此，该类方法存在着一定的局限性［4］。

EEG 信号表现出很强的非线性，熵指数分析方法广泛应用于脑电信号的分析［11-14］，但是单一的熵指数对数据长度较为依赖并且对噪声敏感，不能达到理想的效果［15］。排列熵（Permutation Entropy, PE）作为一种典型的非线性分析方法［16］，具有概念简单、计算时间短、抗噪声能力强等优点，已被用于研究麻醉状态下EEG 信号的复杂性［17-20］，然而，由于高频波的特性，它在突发抑制期间的性能较差［21］。小波熵（Wavelet Entropy,WE）算法是从信号所包含的能量信息角度对信号复杂性的一种度量，对时间序列的非线性动力学特征可以有很好的表达［22-24］。

本文抛弃了现有的计算爆发抑制比的理念（即计算抑制时间段占总时间段的比值），从非线性的角度出发，结合PE 与WE 的计算方法，提出了一种新参数来量化EEG信号的爆发抑制水平。

1 方法与步骤

1.1 数据说明

本研究使用的EEG 数据集来自美国Aspect medical公司生产的BISX 外置模块及数据记录系统，记录了4 名成人全身麻醉状态下手术全过程的EEG信号、BIS 值和SR，这4 例数据中均出现了爆发抑制信号。采集过程中BISX 模块滤波器模式设置为高通0.5 Hz、低通70 Hz、带阻50 & 60 Hz，以256 Hz 的采样率记录EEG 信号，BIS 值与SR 值则每秒输出一次，总共记录约18.08 h。

1.2 BIS模块说明

目前，临床上主要使用BIS监护仪来监测患者的麻醉深度，BIS 主要采用时域分析、频域分析以及双谱分析相结合的方法，利用时域参数SR、β 比率以及同步快慢比综合计算出一个0～100 的无量纲值，0 表示大脑基本没有活动，100表示完全清醒，BIS维持在40～60 的状态被认为是在全身麻醉下进行手术的合适水平［2］。

1.3 计算PE

PE 是一种度量动态时间序列复杂度的物理量，具体计算过程如下：

（1）给定时间序列{x(i),1 ≤i≤N} ;

（2）重构时间序列得：

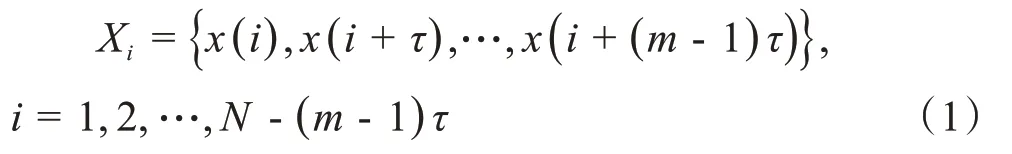
其中，m是重构的维数，τ是延迟时间。

（3）按照递增的顺序对Xi重新排列，会有K=m!种排列方式，P(j) 表示每一种排列方式出现的概率：

（4）归一化的PE定义如下：

PE 值的范围是0～1，PE 值越小，时间序列越规则，反之亦然。PE 的计算取决于数据长度N、嵌入维数m和延迟时间τ的选择。考虑到计算量以及后续处理，排列熵的计算参数N=128，嵌入维数m=3，延迟时间τ=1。

（5）计算PE序列。对预处理后的EEG数据以滑动窗的形式计算PE，窗的大小为1 s（256个点），数据重叠不重叠，根据上述PE 的计算方法得到PE 序列PE(k),k= 1,2,…,T，其中T为采集的EEG数据的秒数。

1.4 计算PE序列的WE

WE 是对信号序列通过小波分解后计算的一种熵值，反映了对信号谱能量在各个子空间分布的有序或无序状态的一种度量，具体的计算步骤如下。

（1）离散小波变换。信号利用离散小波变换可以将信号的低频段与高频段进行分离，将信号分解到正交的子带空间内。将脑电信号分解成细节系数和近似系数:

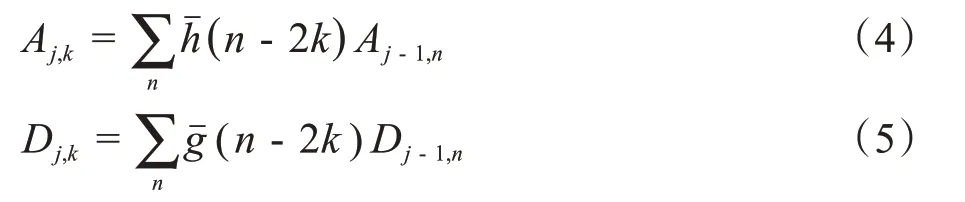
其中，j是分解级别，k是对应的小波系数下标；其中，g(n)为高通滤波器，将滤掉信号的低频分量而输出高频分量，h(n)为低通滤波器，滤掉信号的高频分量而输出低频分量，Aj,k与Dj,k分别表示EEG 信号分解得到的近似系数与细节系数。

（2）计算信号的小波子带能量。信号的子带能量为该子带小波系数的平方和计算而得：

（3）计算小波总能量与相对小波能量（Relative Wavelet,RWE）pj。信号的总能量为分解得到的每个子带信号的能量和：

pj为子带空间能量与信号总能量之比：

（4）计算WE：

（5）计算排列小波熵（PEWE）。对计算好的序列PE(k)进行WE 的计算，选择计算的数据长度为60 个点，也就是60 s计算得到的60个PE值，每次移动1个点；选择db4 小波为母小波，分解层数为5 层，按照上述WE 的计算方法计算PE 序列的小波熵，定义为PEWE。

1.5 计算皮尔逊相关系数

相关系数是用来反映不同变量间相关性程度的统计学指标，本研究使用皮尔逊相关系数来评价PEWE与SR、BIS，以及SR与BIS之间的相关性。

2 结果

图1 是清醒状态下一段60 s 的EEG 信号和计算得到的PE 序列以及PE 序列的RWE，从图1a 中可以看出，清醒状态下的EEG 没有出现爆发抑制模式，所以BIS模块输出SR为0，BIS值为97.7，代表病人此时完全清醒；图1b 中PE 序列也维持在一个较高的水平（0.8～0.9），代表着当前的EEG 信号复杂度较高，并且波动范围很小；图1c 中PE 序列通过小波分解计算得到的RWE 中，低频系数A5 的能量占据绝对主导优势，说明此时的PE 序列能量集中在低频的子带空间内，该频带的RWE 接近于1,而其他频带的相对小波能量接近于0，由此说明当前的PE 序列处于有序状态，计算出的PEWE值非常低，仅为0.040 0。

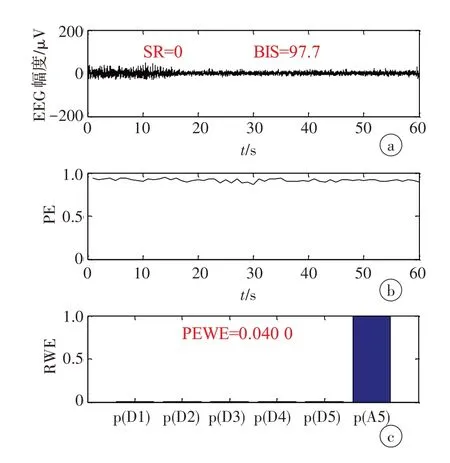
图1 清醒状态下60 s的EEG信号（a）、PE序列（b）和PE序列的RWE（c）Figure 1 EEG signal in the awake state for 60 seconds(a),the calculated PE sequence(b)and RWE of the PE sequence(c)

图2 是深度麻醉状态下一段60 s 的EEG 信号和计算得到的PE 序列以及PE 序列的RWE，从图2a 中可以看出，深度麻醉下的脑电出现了明显的爆发抑制模式，所以此时BIS 模块输出SR 为79.9，BIS 值为8.7，代表病人处于深度麻醉状态；图2b 中PE 序列的值整体降低并随着EEG 中爆发信号与抑制信号的交替出现而产生较大的波动；图2c 中PE 序列通过小波分解计算得到的RWE中，虽然代表低频系数A5的能量仍然占据较大的比例，但跟图1c 比较明显有所降低，并且其他频带的RWE分布并不均匀，此时计算出的PEWE为0.641 5。

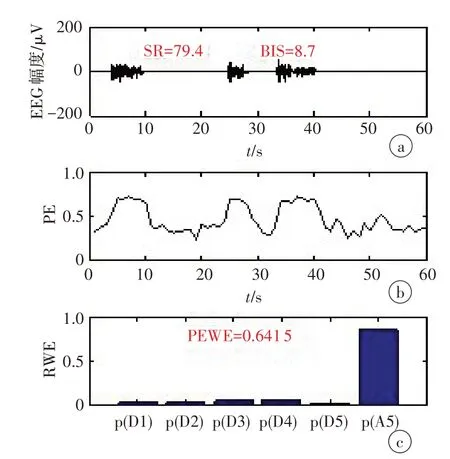
图2 60 s深度麻醉状态下的EEG信号（a）、PE序列（b）和PE序列的RWE（c）Figure 2 EEG signal in the deep anesthesia state for 60 seconds(a),the calculated PE sequence(b)and RWE of the PE sequence(c)

图3 是1 号数据EEG 数据与BIS 模块输出的BIS值以及计算出的PE序列；图4是该例数据BIS模块输出的SR 值以及本文所提出的方法计算出的PEWE。从图3中可以看出，该例数据在手术中出现了爆发抑制信号，并且持续了一段时间，BIS 值在该期间处于一个较低的值，PE 则在爆发抑制期间处于一个震荡的状态；从图4 中可以看出，随着爆发抑制模式的出现，SR值可以比较好的评价病人的爆发抑制水平，而PEWE 在趋势上与SR 值有较强的相关性，相关系数ρPEWE,SR=0.957 1，因此，PEWE 也可以作为评价爆发抑制水平的指标。

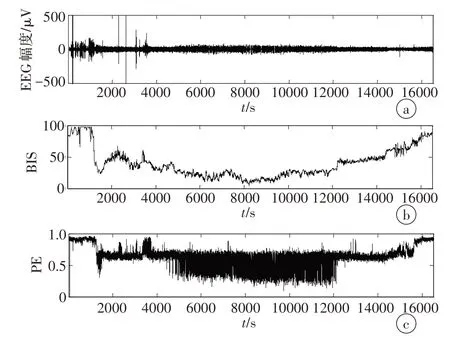
图3 1号数据的EEG信号（a）与BIS值（b）以及计算的PE序列（c）Figure 3 EEG signal(a)and BIS value(b)of No.1 data and the calculated PE sequence(c)

图4 1号数据的SR值（a）与计算的PEWE（b）Figure 4 SR value of No.1 data(a)and the calculated PEWE(b)

图5 是4 例数据计算出的PEWE 和SR 以及PEWE 和BIS 值的散点图，从图中可以看出，PEWE与SR 值呈一定的正向线性相关，PEWE 和BIS 值则呈一定的反向线性相关。

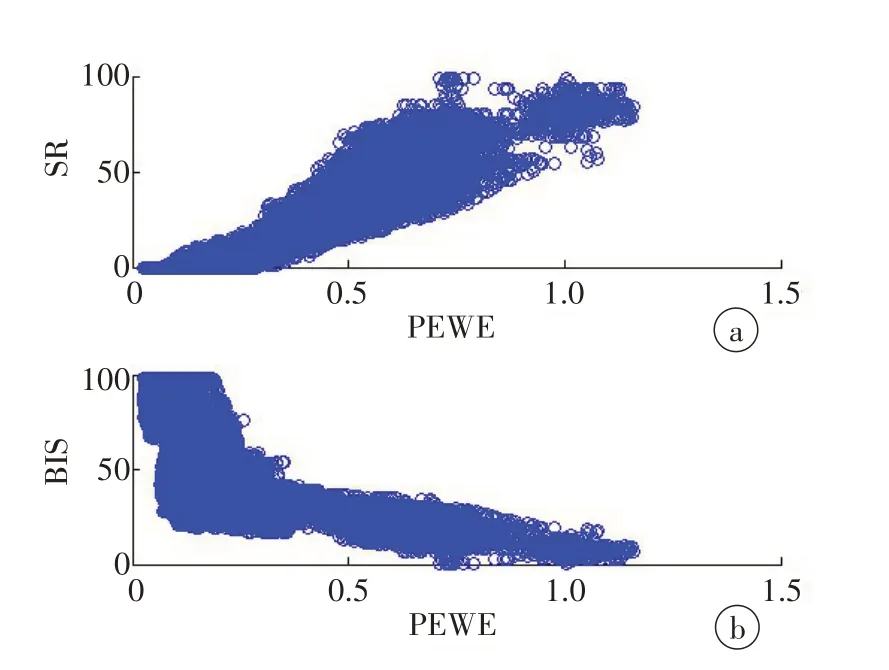
图5 4例数据的PEWE与SR（a）以及PEWE与BIS值（b）的散点图Figure 5 Scatter plots of PEWE and SR(a)and PEWE and BIS(b)in 4 cases of data

表1 是4 例数据PEWE 与BIS、SR 以及SR 与BIS之间相关系数的计算结果，从表中可以看出，4 例数据的PEWE 与SR 的相关系数ρPEWE,SR达0.942 5，表明PEWE 跟SR 有类似的趋势，可以作为一种新参数来量化EEG 信号的爆发抑制水平。从表中还可以看出PEWE 与BIS 的相关系数ρPEWE,BIS在4 例数据中的绝对值均大于SR 与BIS 的相关系数ρSR,BIS的绝对值，说明在计算评估麻醉深度的最终指数时，PEWE可以作为一个比SR更优的子参数组件。

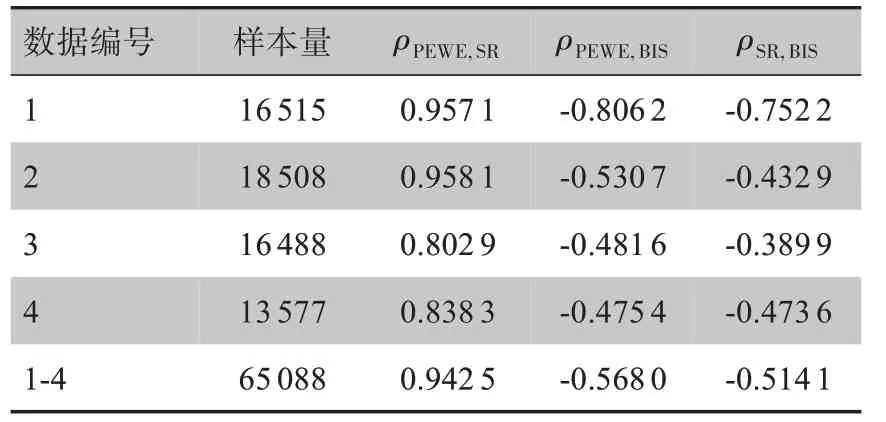
表1 PEWE与BIS、SR以及SR与BIS之间的相关系数Table 1 Correlation coefficients between PEWE and BIS,PEWE and SR,and SR and BIS

3 讨论

本文提出了一种新的参数来量化EEG 信号的爆发抑制水平，通过计算EEG 信号的PE 得到PE 序列，再计算PE 序列的WE 得到参数PEWE。从结果上来看，PEWE 与BIS 模块输出的SR 之间有很高的相关性，因此，PEWE 可以作为一种新参数来量化EEG 信号的爆发抑制水平。其次，基于PE 与WE 的特点，PEWE 具有较强的抗噪能力，并且，由于计算方式的不同，PEWE 相较于SR 包含更多的信息，表1 中的结果也表明了这一点，ρPEWE,BIS在4例数据中的绝对值均大于ρSR,BIS的绝对值，说明在计算评估麻醉深度的最终指数时，PEWE 可以作为一个比SR 更优的子参数组件，加入到计算当中。

PEWE 也有一些局限性，首先，PEWE 基于熵的角度来量化EEG 信号的爆发抑制水平，在无爆发抑制信号时该参数并不为0，而是维持一个较低的值，这给解释爆发抑制水平的量化结果带来了一些困难；其次，本文也没有测试PE 的嵌入维数和延迟时间，以及WE 的分解层数给最终结果带来的影响，这些参数目前均是基于经验选取的；最后，本文所用的数据样本较少，没有考虑到人体EEG 的高变异性。这些局限性将在我们今后的工作中予以克服。

4 结论

本文从非线性的角度出发，结合PE 与WE 的计算方法，提出了一种新的参数PEWE 来量化EEG 信号的爆发抑制水平。结果表明，PEWE 与SR 具有较高的相关性，说明PEWE可以作为一种新参数来量化EEG 信号的爆发抑制水平，为量化EEG 信号的爆发抑制水平提供了新思路；并且PEWE 与BIS的相关性高于SR 与BIS 的相关性，所以，PEWE 可以作为一个比SR 更优的子参数组件，加入到麻醉深度监测的计算中，期待后续的进一步研究及优化。