应力波无损检测技术定量评价木构件材料性能研究
尹婷婷
上海建工集团工程研究总院 上海 201114
1 背景
我国现存许多木结构建筑,而木结构建筑在长期服役期间会因环境或人为因素产生损坏,亟需加固和修复[1]。在加固修复之前往往需要检测木材的力学性能,传统检测方法是采用万能力学试验机对木材清材试件进行破坏性试验。这种检测方法获得的结果比较准确,但耗时长,需要拆卸构件取样进行破坏检测。如何满足不损坏或拆卸木构件的检测要求,更准确、更有效地对木材的力学性能进行无损检测和评价,已经成为亟待解决的问题。
本研究针对木结构构件的常用树种,开展应力波无损检测技术定量评价木构件材质力学性能的关键技术研究,建立两者的关系模型,为木构件的现场无损检测工作提供依据。
2 试验原理
应力波是一种可在物体内部传播的机械波,在传播过程中会沿着最短路径传播,即在均匀介质中,它是沿直线传播的,在非均匀介质中,其传播的路径变长,导致传播时间增长,这是应力波法应用的最基本理论[2-3]。木材纵向应力波无损检测技术则主要用于测定木材的弹性模量,评估木材的力学强度。
应力波在木材中的传播速度、木材的密度及弹性模量间存在如下物理关系:E=ρv2。其中,E为应力波测试的动弹性模量(单位:Pa),ρ为木材密度(单位:kg/m3),v为应力波在该木材中的传播速度(单位:m/s)[4-5]。
依据应力波传播的基本原理,在木材长度方向设置2个传感器,分别为传感器1和传感器2。敲击传感器1,使其内部产生应力波的传播,通过测量传感器2接收应力波的传播时间(图1),由传感器距离除以对应的传播时间,即计算得到传播速度[6-7]。

图1 应力波无损检测示意
本研究将花旗松材料制成标准试件,分别测试标准试件的应力波传播速度、物理性能、力学性能等参数,最后拟合木材力学性能与动弹性模量的公式,提高木材应力波无损检测的精确度和有效性。
3 材料和方法
3.1 试验材料
试验材料采用花旗松。原材料沿顺纹径向加工成标准尺寸的清材小试件(20 mm×20 mm×500 mm),试件首先用于应力波波速测定试验。
无损检测完成后,将上述清材小试件加工成2个木材密度试件(20 mm×20 mm×20 mm)、1个顺纹抗压强度试件(20 mm×20 mm×30 mm)、1个抗弯性能测试试件(20 mm× 20 mm×300 mm)。
3.2 测试方法
1)应力波波速测定:采用匈牙利生产的ARBORSONIC应力波测量仪检测。测定时,2个传感器探针插入试件两端,探针与试件长度方向夹角在30°~45°。连续敲击3次,传播时间取平均值。
2)含水率测定:根据GB/T 1931—2009《木材含水率测定方法》进行。
3)密度测定:根据GB/T 1933—2009《木材密度测定方法》进行。
4)弯曲性能测试/弹性模量:依据GB/T 1936.1—2009《木材抗弯强度试验方法》进行。
5)顺纹抗压测试:依据GB/T 1935—2009《木材顺纹抗压强度试验方法》进行。
试件物理性能和力学性能测试见图2。

图2 物理性能和力学性能测试
4 结果与分析
4.1 应力波无损检测评价花旗松材质清材力学性能
试验测得花旗松相关物理性能、力学性能和应力波传播数据,并通过应力波传播速度v和密度ρ,由公式E=ρv2获得动弹性模量(表1)。
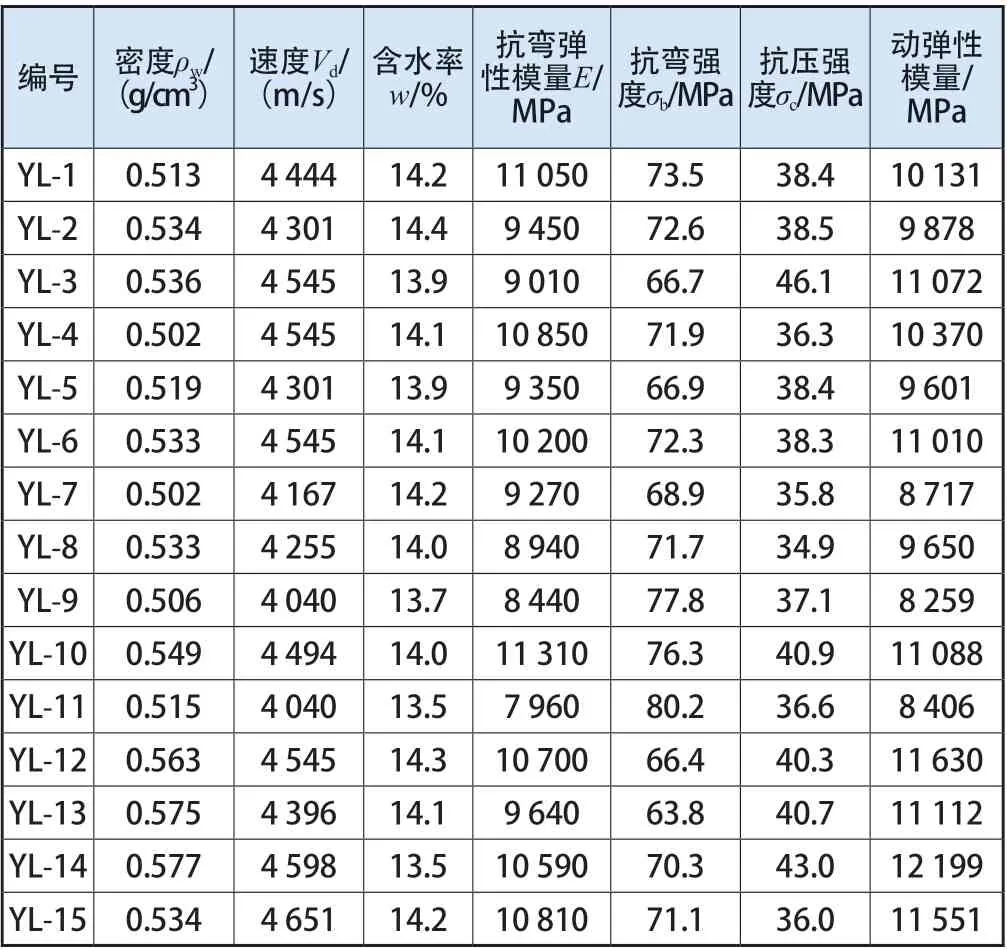
表1 花旗松相关物理力学性能及应力波检测数据
通过线性回归分析生成动弹性模量(ρv2)和实测结果抗弯强度、弹性模量以及抗压强度的关系公式,分别分析材质性能和ρv2的相关性。
4.1.1 动弹性模量与花旗松抗弯弹性模量关系
以万能力学试验机测得的花旗松含水率w时的抗弯弹性模量E为应变量(y),以动弹性模量(ρv2)为自变量(x),对其进行统计分析,所得回归模型及相应的数学表达式和决定系数如图3所示。
由图3可以得知:花旗松弹性模量与应力波测得的动态弹性模量之间有统计上的线性关系,其回归方程为E=0.612 1ρv2+3 526.2,决定系数为R2=0.525 3,决定系数R2>0.5,为强相关。

图3 抗弯弹性模量-动弹性模量(ρv2)关系
由此可见,通过应力波测得的动态弹性模量可以推测材料的弹性模量。通过回归分析,得到0.001<P-value<0.010,具有非常显著的意义。
研究表明,应力波属低频率波,传播距离长,能对大跨径构件的性能给予一个均衡的评价,故应力波测试的动弹性模量能接近静弹性模量,但往往比静弹性模量高[8-9]。本文研究基本符合以上结论,由于试件为清材小试件或测得误差造成少量数据不符合。
4.1.2 动弹性模量与花旗松抗弯强度关系
以万能力学试验机测得的花旗松含水率w时的抗弯强度σb为应变量(y),以动弹性模量(ρv2)为自变量(x),对其进行统计分析,所得回归模型及相应的数学表达式和决定系数如图4所示。

图4 抗弯强度-动弹性模量(ρv2)关系
由图4可以得知:花旗松抗弯强度与应力波测得的动态弹性模量之间有统计上的线性关系,其回归方程为σb=-0.001 8ρv2+90.172,决定系数为0.246,为弱相关。通过回归分析,得P-value>0.05,说明应力波测得的动态弹性模量与抗弯强度之间线性关系不显著。
4.1.3 动弹性模量与花旗松抗压强度关系
以万能力学试验机测得的花旗松含水率w时的抗压强度σc为应变量(y),以动弹性模量(ρv2)为自变量(x),对其进行统计分析,所得回归模型及相应的数学表达式和决定系数如图5所示。

图5 抗压强度-动弹性模量(ρv2)关系
由图5可以得知:花旗松抗压强度与应力波测得的动态弹性模量之间有统计上的线性关系,具体的回归方程为σc=0.001 5ρv2+23.722,决定系数为0.345 1,0.3<R2=0.345 1<0.5,为中等相关。
由此可见,通过应力波测得的动态弹性模量可以推测材料的抗压强度。通过回归分析,0.01<P-value<0.05,得到的结果具有显著性意义。
4.2 应力波无损检测评价不同树种力学性能研究
4.2.1 树种对应力波无损检测值的影响
为分析树种对应力波无损检测值的影响,基于花旗松测试数据,再选取樟子松、菠萝格2个树种各6个检测数据(表2)作为分析样本,分析不同树种间应力波传播速度是否有差异。
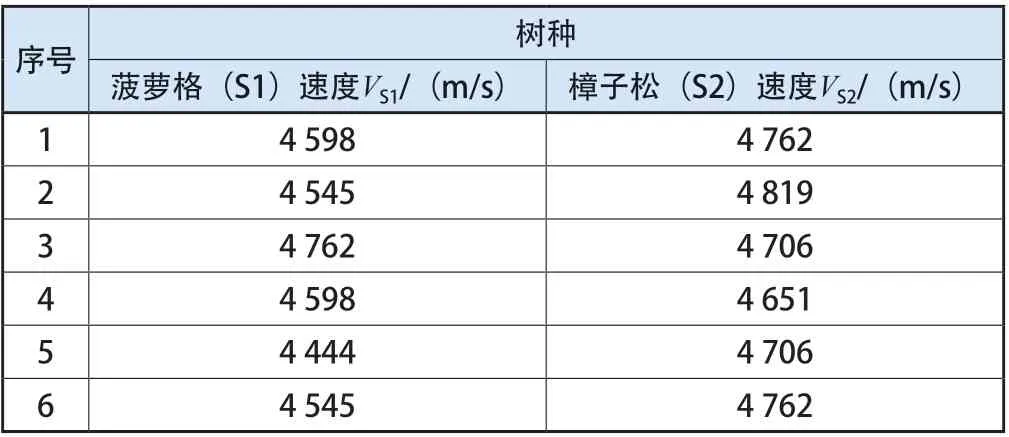
表2 樟子松、菠萝格应力波传播速度
通过Excel对花旗松、樟子松、菠萝格应力波传播速度3组数据进行单因素方差分析,可以得到如下结果:F=10.514>F-crit=3.402,且P-value=0.000 525<0.05,所以花旗松、樟子松、菠萝格3种不同树种间的应力波传播速度具有显著差异性。由此可见,不同树种对应力波传播影响较大。
4.2.2 树种对模型预测精确性的影响
为分析模型(4.1节中得到的材料性能预测模型)的适用度,本试验测得樟子松、菠萝格2个树种的检测数据,对此进行验证,通过无损检测结果计算得到动弹性模量(ρv2),代入上述模型计算得到预测值,将预测值与实测结果进行对比,分析误差大小(表3、表4)。
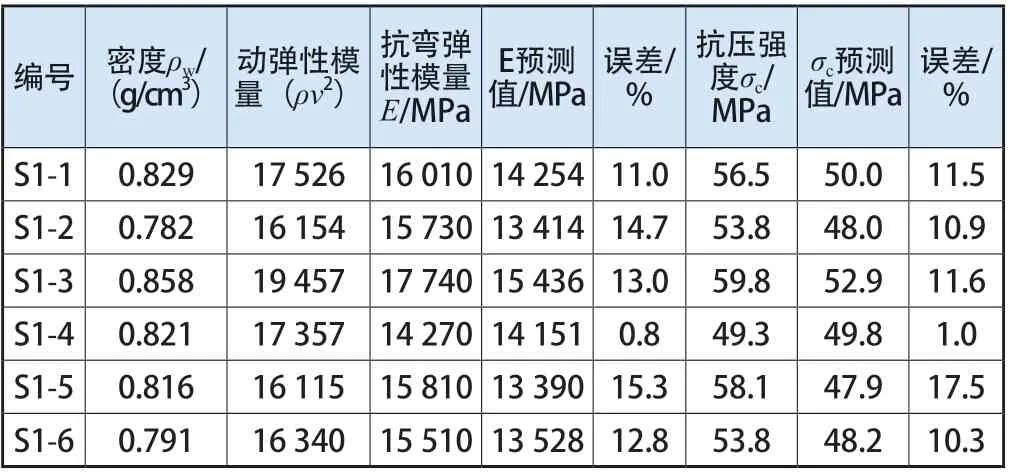
表3 菠萝格力学性能预测值与实测值对比
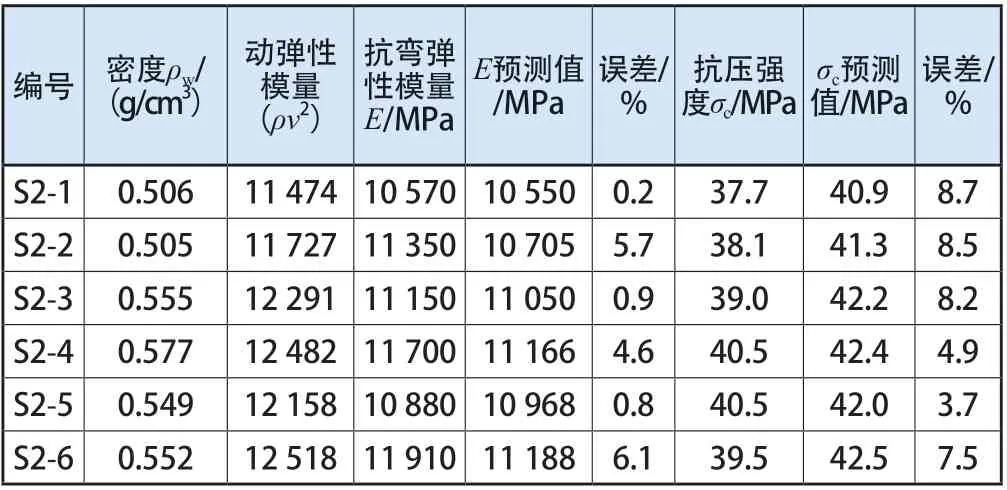
表4 樟子松力学性能预测值与实测值对比
结合表2的数据,由测得的各试件波速v和密度ρ,得到动弹性模量。将相关数据代入花旗松清材试件得到的应力波无损检测力学性能预测模型中,其中,预测抗弯弹性模量和抗压强度模型具有显著相关性,抗弯弹性模量预测模型为E=0.612 1ρv2+3 526.2,抗压强度预测模型为σc=0.001 5ρv2+23.722。抗弯强度不具有显著相关性,因而不进行分析。通过数据分析,将得到的预测结果与实测结果进行对比,分析误差大小。
由表3中数据可以得知,对菠萝格预测弹性模量和抗压强度的平均相对误差分别为11.3%和10.1%。由表4中数据可以得知,对樟子松预测的平均相对误差分别为2.8%和6.9%,说明模型对不同树种的力学性能预测效果皆较为良好,模型适用性较高。
通过对比可见,对樟子松预测精度更高,可能是因为樟子松与花旗松都为针叶材,且两者平均密度接近。该预测模型仍然是通过应力波数据预测木材力学性能的一种有效方法,而该模型对于其他不同树种的适用程度与有效性还有待进行进一步研究。
5 结语
通过研究得到以下结论:
1)弹性模量与应力波测得的动态弹性模量之间有较好的线性关系,其回归方程为E=0.612 1ρv2+3 526.2,决定系数为0.525 3。
2)抗弯强度与应力波测得的动态弹性模量之间有一定的线性关系,其回归方程为σb=-0.001 8ρv2+90.172,决定系数为0.246。
3)抗压强度与应力波测得的动态弹性模量之间有较好的线性关系,其回归方程为σc=0.001 5ρv2+23.722,决定系数为0.345 1。
4)不同树种对应力波传播的影响较大,应力波无损检测对于其他树种的力学性能预测模型还有待进行进一步的研究。

