圆柱分层各向异性地层中偏心线圈电磁场闭合解
陈 华,洪德成,武圣哲
(1.中国石油大学(华东)理学院,山东青岛 266580;2.吉林大学物理学院计算方法与软件国际中心,吉林长春 130012)
21世纪初,为探测砂泥岩薄交互层组这类低阻油储层宏观电各向异性信息,电缆感应测井仪器由传统单一分量的轴向型仪器发展到多分量感应仪器(也称为三轴感应仪器),可以测量同一空间位置上9个磁场分量[1]。它们构成空间矢量场完备集,用于反演电导率各向异性、地层边界位置及方位信息。以此为借鉴,随钻电磁波测井仪器也由传统无方位性的轴向型仪器发展到以倾斜线圈或正交线圈为基本结构单元的方位电磁波测井仪器[2-4]。在理论研究方面,水平层状分层地层和圆柱状分层地层是仪器工作原理分析、参数优化设计和测井资料处理的基础模型[5-9]。圆柱状分层地层主要用于电缆测井及随钻测井的井眼环境影响校正及仪器径向响应特征分析。正演模拟方法与发射源类型、地层几何结构和电学性质等参数有关。发射源一般分为磁偶极子源与电流源:磁偶极子源可以是任意方向磁偶极子或三轴正交磁偶极子[7-9];电流源考虑发射线圈几何形状,包含倾斜线圈和水平线圈。圆柱几何结构包括共轴多层和偏心多层;其电学性质主要包含电导率各向同性和单轴各向异性。早期针对水平线圈,Chew等[10-11]分别推导了共轴各向同性地层和偏心各向同性地层中仪器响应正演解析算法。直到2003年,Hagiwara等[12]给出了共轴各向同性地层居中倾斜线圈正演解析算法。在此基础上,Hue[13]将该工作推广到偏心各向同性地层。Liu等[14]进一步推导了多重偏心单轴各向异性地层中倾斜线圈的正演解析算法。国内学者魏宝君等[15-16]对柱状分层介质居中倾斜线圈及偏心水平线圈电磁场的解析解分别做了深入研究。值得注意的是上述工作均采用Chew给出的广义反射/透射递推系数描述电磁波在柱状分层介质中的传播。在频率-波数域中其解析公式包含单独存在的贝塞尔函数和汉克尔函数。这类柱函数的宗量为复数,当其虚部增加时会引起发散,造成积分计算过程中的数值溢出问题,为计算机编程带来不便。Hong等[17]推导了一组新的无溢出广义反射/透射系数,以柱函数比值为基本单元,从解析公式的表达上解决了数值溢出这个难题。随后,分别给出了水平线圈和倾斜线圈在偏心地层中接收线圈电压正演解析算法[18-20]。在求解偏心问题的几何模型中,偏心线圈内仍可含有共轴多层介质[11,13-14,18-20]。这类模型可用来考察仪器钻杆对测井响应的影响,但由于内部柱状介质的电磁散射作用,需要通过矩阵方程求解电磁场分量的驻波和外行波系数。这使得其解析表达式是非闭合的,不便于对线圈偏心引起的电磁场角模量耦合关系进行数理分析。当线圈放置在最内层时可得到其闭合的解析表达式,便于物理参数之间关系的考察。考虑到电缆测井仪器的玻璃钢芯棒对电磁波影响较小,随钻测井仪器接收线圈的相对测量值受金属钻杆的影响可以忽略或为恒定值,求解线圈在最内层偏心正演问题也具有实际应用价值。笔者针对共轴圆柱各向异性地层推导倾斜电流源在最内层偏心时激发电磁场的解析解闭合表达式,分析角模量耦合强度随偏心距变化关系;给出共轴倾斜线圈系电压解析解,分析当发射/接收线圈水平放置时电压表达式的退化过程。最后,通过数值模拟研究接收线圈电压与仪器参数、地层参数及偏心参数的变化关系。
1 偏心线圈正演模型
图1给出了共轴圆柱地层中偏心线圈系的3种结构。共轴的任意倾斜发射/接收线圈如图1(a)所示,为中海油服公司随钻测井仪器基本结构单元[18]。发射线圈径向半径ρT与接收线圈径向半径ρR大小相同,即ρT=ρR。φT和θT分别为发射线圈方位角与倾斜角;φR和θR分别为接收线圈方位角与倾斜角。当发射线圈水平放置时,物理模型简化为图1(b),为斯伦贝谢方位电阻率测井仪器PeriScope基本结构单元[2]。当发射线圈和接收线圈均水平放置时,物理模型进一步简化,如图1(c)所示,为传统轴向型电缆感应测井仪器和随钻测井仪器基本机构单元[11]。
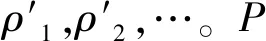

图1 圆柱状分层地层中的偏心线圈Fig.1 Eccentric coil in a cylindrical layered stratum

图2 圆柱状分层地层中的偏心线圈俯视图Fig.2 Top view of eccentric coil in cylindrical layered formation
2 正演计算方法
2.1 均匀地层中的电磁场
倾斜线圈加载电流IT=I0exp(-iωt),在空间中激发交变电磁场。在圆柱坐标系下通过TE/TM波分解技术实现电磁场正交分解。为匹配圆柱面边界条件,需首先通过傅里叶变换将电磁场分量转换到波数域:

(1)
在波数域中,电磁场z分量为多重角模量的叠加,其在均匀各向同性介质中的表达式[12,20]为

(2)
其中
cTE=iνJν(kzρTtanθT)exp(-i(kzzT+νφT)).
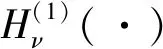

(3)

(4)
2.2 圆柱状分层地层中的电磁场
将线圈放置在圆柱分层地层最内层。在仪器坐标系下,以线圈半径为界,电磁场内区间表达式[20]为

(5)
外区间表达式为

(6)
式(5)和(6)中的右侧第一项为来自界面的反射场,第二项代表由发射源产生的背景场。
在地层坐标系下,电磁场一般表达式为
(7)
Jν′-ν(γd)exp(-i(ν′-ν)φE)),
Jν′-ν(γd)exp(-i(ν′-ν)φE).
(8)


(9)
与式(8)比较,有

(10)

(11)


(12)
因为ν与ν′为不同的求和指标,式(12)进一步改写为

(13)
在等式两侧乘以常数Jν′-ν″(γ1d)exp(i(ν′-ν″)φE),ν″为任意整数,整理得

(14)
式(14)对任意ν′阶模量都成立,所以对其所有模量求和也成立:

(15)
交换求和顺序,得


(16)
利用Graf加法定理[8]:

(17)
其中
式(17)化简为
exp(i(ν-ν″)φE)a1,ν.
(18)
进一步改写为

(19)


(20)


(21)
将式(21)代入式(5)或(6)即可求出仪器坐标系下电磁场垂直分量闭合表达式:


(22)
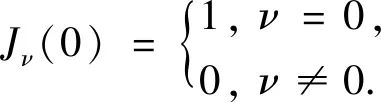
(23)
代入式(21),得

(24)

(25)
所有角模量解耦,驻波为相同角模量外行波的广义反射波。
2.3 倾斜线圈系电压
在仪器坐标系下任意倾斜发射-接收线圈,如图1(a),电压表达式[12]为

(26)
积分核:
dTM(ν,kz)ez,ν(ρR,kz)].
(27)
其中
dTE(ν,kz)=i-νJν(κR),
κR=kzρRtanθR.
ez,ν为电场z-分量的ν阶模量,由式(5)和(6)得

(28)
eφ,ν为电场φ-分量的ν阶模量,利用公式(3)得
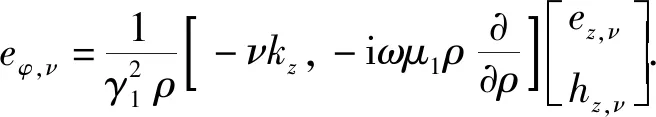
(29)
驻波系数b1,ν已由式(19)求出,将式(28)和(29)中相应电场分量代入到式(26)、(27)中即可求出倾斜线圈电压。
数理分析显示,当发射-接收线圈径向半径相等时,式(28)右侧第二项,即背景场,收敛缓慢。为提高数值积分的计算精度与计算效率,接收线圈电压计算式(26)中只对反射场积分。反射电场对应分量为

(30)

(31)
背景场对应电压求解则采用空间域变量二重有限区间积分[12],即
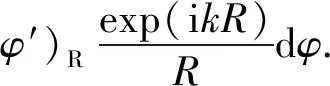
(32)
2.4 水平线圈系电压
(1)当发射线圈水平放置,发射线圈仍为任意方位倾斜时,如图1(b),积分核(26)进一步简化。令θT=0,结合贝塞尔函数在原点处的性质(23)及式(3)知,水平线圈只激发电磁场零阶模量,即

(33)
将式(33)代入式(22),得

(34)
其中

(35)
式(35)即由(20)脚标互换νν″并令ν″=0得到。可见,虽然水平线圈只激发电磁场零阶模量,但经偏心边界反射后,仍耦合出其他高阶模量。
(2)当发射线圈水平放置,接收线圈也水平放置时,如图1(c)。接收线圈倾斜角θR=0。积分核(27)进一步简化得
w(kz)=-ρRγ1eφ,0(ρR,kz).
(36)
其中
2.5 柱函数及其数值溢出问题


(37)


(38)


表1 解析算法计算结果与有限体积法计算结果统计Table 1 Results comparison between analytical algorithm and finite volume method
3 数值模拟
3.1 计算方法验证
考虑三层各向异性地层模型。最内层为井眼,半径为22.86 cm,电导率σ1=0.01 S/m;第2层为侵入带,半径为30.48 cm,水平电导率σh,2=0.5 S/m,垂直电导率σv,2=0.062 5 S/m;第3层为原状地层,水平电导率σh,3=1 S/m,垂直电导率σv,3=0.1 S/m。发射-接收线圈径向半径ρT=ρR=11.43 cm,电流强度IT=1安培,发射频率f=2 MHz。发射线圈位置zT=0;接收线圈位置zR=99.06 cm。其他参数及计算结果见表1。与有限体积法对比[21],相对误差小于0.5%,验证了本文算法的正确性。基于该模型,考虑仪器响应随各参数变化关系。
3.2 水平发射-水平接收线圈系
当发射线圈-接收线圈均水平放置时,倾斜角θT=0°,θR=0°;由式(38)知电压只与偏心距d有关,与发射/接收线圈方位φT、φR及偏心角φE无关。图3给出了电压随偏心距d变化关系。可以看出随着偏心距的增加,电压实部和虚部信号与居中时的数值偏离增加。虚部信号居中时为负值,当偏心距很大时则可变为正值。令σv,2=0.5 S/m,σv,3=1 S/m,即各向同性地层。当仪器居中时,感应电场空间部分为共轴的同心圆,地层中的感应电流大小只与水平电导率有关,与各向异性无关,所以从图3上可以看出此时当接收线圈上的电压与各向异性无关;但当仪器偏心时对称性破坏,电压受各向异性影响,且随着偏心距的增加各向异性影响增加。
令侵入带为各向同性,σh,2=σv,2=0.5 S/m,原状地层为各向异性,图4给出了偏心距为0.101 6 m时电压随地层水平电导率变化规律。可以看出,当地层水平电导率小于0.1 S/m时,各向异性影响可以忽略;当地层水平电导率较大时电导率各向异性影响明显增加。

图3 水平发射-水平接收线圈系电压随偏心距变化Fig.3 Voltages of horizontal transmitter-horizontal receiver along with eccentric distance

图4 偏心距0.101 6 m时电压随偏地层水平电导率变化规律Fig.4 Voltages along with horizontal conductivity of formation for eccentric distance of 0.101 6 m
保持原接收线圈zR1=0.990 6 m,增加接收线圈zR2=0.787 4 m,定义两个接收线圈电压信号的幅度比和相位差:
s=|V1|/|V2|,Δφ=φ1-φ2.
(39)
从图5可以看出,幅度比和相位差均随着偏心距增加而减小。当仪器居中时,幅度比和相位差与各向异性无关;当仪器偏心时候幅度比和相位差与向异性有关,偏心距越大,受各向异性影响越大。该结论与图3中单个线圈电压受各向异性影响规律一致。

图5 相对测量值随偏心距变化Fig.5 Relative measures between two receivers against eccentric distance
3.3 水平发射-倾斜接收线圈系
当发射线圈水平放置,接收线圈倾斜时,令θR=45°,方位角φR=0°;偏心距d分别为0.025 4,0.050 8,0.076 2,0.101 6 m。图6给出了各向同性地层中电压随偏心方位φE变化关系。在相同偏心距情况下,接收线圈电压信号随方位角近似余弦变化关系。该结论也可由式(34)看出,但考虑到多阶模量的叠加作用,并不满足严格的余弦变化关系。图7显示各向异性地层中电压随偏心方位φE变化规律与各向异性地层中的基本相同,但变化幅度略小。图8给出了当偏心距为0.101 6 m时两接收线圈间的幅度比和相位差随φE变化规律。与图5中水平接收线圈的模拟结果比较,可以看出倾斜接收线圈的幅度比变化规律更为复杂,相位差变化强度更大。

图6 各向同性地层中水平发射-倾斜接收线圈系电压随偏心方位变化Fig.6 Voltages of horizontal transmitter-tilted receiver system along with eccentric angle in isotropic formation

图7 各向异性地层中水平发射-倾斜接收线圈系电压随偏心方位变化Fig.7 Voltages of horizontal transmitter-tilted receiver system along with eccentric angle in anisotropic formation

图8 相对测量值随偏心方位变化Fig.8 Relative measures between two receivers again eccentric angle
3.4 倾斜发射-倾斜接收线圈系
当发射线圈水和接收线圈均倾斜时,影响电压信号的因素很多,这里只给出电压与方位角变化关系。令发射线圈θT=-45°,0°,45°,φT=0°;接收线圈θR=45°,φR=0°;偏心距d=0.076 2 m。图9给出了各向同性地层中接收线圈电压随方位角变化规律。可以看出,不同发射线圈倾斜角的电压差别很大。倾角θT=0°为斯伦贝谢方位电阻率测井仪器PeriScope基本结构单元[2],倾角θT=-45°时收发线圈对称放置,为海油服公司随钻测井仪器基本结构单元[22],它们都要比倾角为θT=45°时受偏心角影响大。
图10给出了各向异性性地层中接收线圈电压随方位角变化规律。与各向同性地层相比较,除了幅值大小略有不同外,变化规律相同。图11给出当发射线圈倾角为θT=45°时各向同性地层与各向异性地层中幅度比与相位差的比较。它们的变化规律基本相同,随偏心角增加相对变化幅度不大,但受各向异性影响明显。

图9 各向同性地层中倾斜发射-倾斜接收线圈电压随偏心方位变化Fig.9 Voltages of tilted transmitter-tilted receiver along with eccentric angle in isotropic formation

图10 各向异性地层中倾斜发射-倾斜接收线圈电压随偏心方位变化Fig.10 Voltages of tilted transmitter-tilted receiver along with eccentric angle in anisotropic formation

图11 相对测量值随偏心方位变化Fig.11 Relative measures between two receivers again eccentric angle
4 结束语
针对圆柱状分层各向异性介质,推导了倾斜线圈在最内层偏心时电磁场解析解的闭合表达式,并讨论了角模量在界面处的反射及耦合关系。给出了偏心倾斜发射-倾斜接收线圈系电压积分表达式,讨论了线圈水平放置时电压表达式的简化过程以及如何避免积分过程中的数值溢出问题。数值模拟结果显示对于无方位的水平发射-水平接收共轴线圈,仪器偏心时电压信号仍会受到电导率各向异性影响;对于有方位的倾斜接收线圈,偏心距、偏心方位、电导率各向异性对电压信号的实部、虚部以及两接收线圈间的幅度比、相位差均有很大影响,且影响规律复杂,这些影响将为方位电磁波测井仪器的井眼环境校正带来很大的挑战。

