以p,Vm为参数的范德华气体的焦耳-汤姆逊系数及μJ-T-p-T图像

冯祥明，郑金云，陈卫华，关新新，张建民

郑州大学化学学院，郑州 450001

1 前言

节流膨胀是制冷和气体液化的重要方法，以其制备的液态气体用途广泛，如液氮，作为低温冷源，在科研、医疗和工农业生产中均有广泛的应用，因此该部分内容与实际应用联系密切，在物理化学教学中具有现实的价值和意义。目前主要物理化学参考资料和文献中对节流膨胀的讨论多立足于等焓过程等热力学分析[1]，较少讲解和讨论气体状态参数对温度变化的影响，同时由于缺乏直观的图像，也造成学生对该部分内容产生较多的疑问和困惑，影响了学习效果。

实际气体的节流膨胀相对复杂，为了达到一定的教学效果，以范德华气体代替实际气体，既能够在一定程度上反映实际气体的行为，同时又避免引入过于复杂的推导和计算[2]。通过文献调研发现，目前对于讨论范德华气体节流膨胀的资料相对较少，部分参考资料和文献只给出了低压条件下[3]，或符合p(Vm− b) = RT方程气体的焦耳-汤姆逊系数(μJ-T)[4]，未在更广泛的条件下描述状态参数对范德华气体μJ-T的影响，因此有必要在此基础上进一步深入讨论。

焦耳-汤姆逊效应(Joule-Thomson effect)指气体通过多孔塞膨胀后所引起的温度变化现象，1852年由英国物理学家J. P. 焦耳和W. 汤姆逊在研究气体的内能时发现，随后引发了一系列对于气体液化和低温的研究，具有重要的教学价值和意义。焦耳-汤姆逊系数(μJ-T)定义为等焓条件下，温度随压强的变化率，即(∂T/∂p)H，其与气体状态的关系可表示为[5]：

对于理想气体或符合p(Vm− b) = RT方程的气体，很容易得到(∂Vm/∂T)p，进而计算出μJ-T。但是对于符合范德华方程的气体一般难于直接得到(∂Vm/∂T)p，这也是相关资料较少的原因之一。

文献[6]利用p,Vm,T的循环关系将不易直接求解的(∂Vm/∂T)p转变为能够由范德华方程求解的(∂p/∂T)Vm/(∂p/∂Vm)T，从而得到包含T,Vm两个参数的范德华气体的焦耳-汤姆逊系数：

上式中a和b为范德华气体常数。由于该式在推导时未引入额外的限制条件，因而具有更广泛的适用性。

在形式上，μJ-T除了可以是T,Vm的函数外，也可以是p,Vm或p,T的函数。本文经过尝试，可利用范德华方程直接得到(∂Vm/∂T)p，进而得到以p,Vm为参数的μJ-T。

2 μJ-T = μ(p,Vm)的推导

对理想气体而言：a = 0，b = 0，所以μJ-T= 0；

对符合p(Vm− b) = RT的气体而言：a = 0，所以μJ-T= −b/Cp。

同时通过验证，该式与文献[6]中以T，Vm为参数的焦耳-汤姆逊系数完全等价。

3 μJ-T-p-T三维图像

相对p,Vm而言，p,T更易直接测量，以其为参数表示μJ-T更方便和直观。在形式上可通过范德华方程解出体积Vm，带入μJ-T= μ(p,Vm)或μJ-T= μ(T,Vm)得到以p,T为参数的μJ-T。但经过尝试，推导过程过于繁琐，且最终结果也无法直观反映出p,T对μJ-T影响。而采用图像展示的方法，不仅可以较直观地体现出μJ-T与p,T的关系，同时也回避了繁琐的公式推导。此外，范德华方程仅为定性或半定量模型，只需通过图像反映出p,T的影响，满足教学效果即可。

μJ-T= μ(p,T)中含有两个参数，难以在二维平面图中直接体现，因此采用三维图像反映μJ-T与p,T的关系更佳。

另外，由于缺少μJ-T= μ(p,T)的表达式，无法直接作图，但在利用(3)式计算μJ-T时可以将p,Vm带入范德华方程后得到相应的T，从而得到对应的p,T和μJ-T，满足作图要求。这里以氮气为例绘制μJ-T-p-T三维图像。

氮气的范德华方程为[5]：

p单位为kPa，Vm单位为L·mol−1。p的选取范围为0.1-40000 kPa，温度范围为148-448 K。

采用上述方法，将相应的μJ-T-p-Vm转变为μJ-T-p-T后进行作图，得到的μJ-T= μ(p,T)三维图形如图1所示。

图1中蓝色为制冷区域，橙色为致热区域。可以看出，三维图像非常简洁地反映出μJ-T，p,T之间的关系。该图不仅可以确定制冷和致热区域，同时也反映出不同p,T对μJ-T大小的影响，即在适当的低温和低压下，氮气具有更高的μJ-T。此外，利用数据也可以绘制p,T二维等高线图，如图2所示。

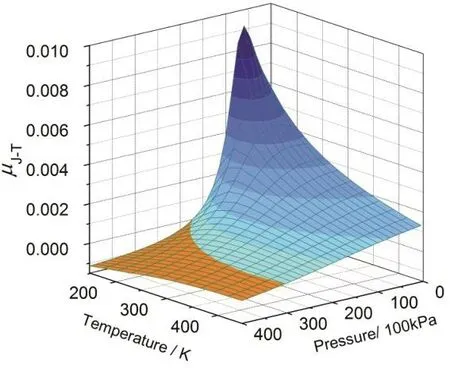
图1 氮气的μJ-T-p-T三维图像

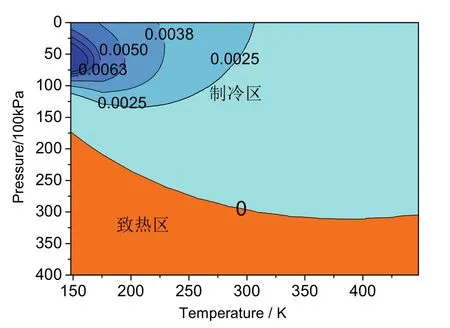
图2 氮气的μJ-T-p-T二维等高线图像

同样，在p,T二维等高线图中可以非常清晰地确定μJ-T为正的区域。需要说明的是图中制冷区域与文献报道相比有一定差别[7]，主要原因为所用的氮气范德华方程适用范围有限。

4 结语

通过推导包含体积和压力的范德华气体的焦耳-汤姆逊系数，对节流膨胀部分的内容进行了进一步讨论；并且利用得到的结果，将μJ-T= μ(p,Vm)转化为更直观的μJ-T= μ(p,T)三维图像和二维等高图，避免了繁琐的公式推导，以期望达到更好的教学效果。