基于HLRF 法与修正对称秩1 方法的改进可靠度方法

范文亮，刘 丞，李正良

(1. 重庆大学土木工程学院，重庆 400045；2. 山地城镇建设与新技术教育部重点实验室(重庆大学)，重庆 400045)

在结构可靠度分析领域，研究者经常使用概率分布模型来描述目标结构的荷载、材料属性等不确定性因素。为考虑这些不确定性因素对结构性能及安全性的影响，发展准确而有效的可靠度分析方法是非常必要的。

一次可靠度方法[1-7]是最常用的可靠度分析方法。其中的验算点法(即Hasofer-Lind-Rackwitz-Fiessler 方法，简称HLRF 法)以其迭代格式简单、收敛迅速，被广泛应用于求解可靠指标，且研究者针对HLRF 法在面对复杂问题时常出现的迭代迂回振荡甚至不收敛的问题，发展了一系列改进的HLRF 法[8-11]。由于验算点的迭代计算在形式上可以表示为一个约束优化问题，通过引入拉格朗日乘子可得到与之等效的无约束优化方程，因此，将收敛性能更优的无约束优化方法(如拟牛顿优化方法等)引入可靠度分析是可行的研究方向。文献[12]将拟牛顿优化方法中的BFGS(Broyden-Fletcher-Goldfarb-Shanno)方法[13]引入可靠度分析，并结合HLRF 法的步长参数，提出了HLRF-BFGS方法，避免了传统方法中的步长搜索过程，改善了计算效率。

一次可靠度方法采用了功能函数在验算点处的线性近似，因此对于功能函数非线性程度较高的强非线性问题，可靠指标的精度往往很难保证。为此，在一次可靠度方法的基础上，若引入功能函数在验算点处的二次函数近似，并以此为基础计算可靠指标，则形成了二次可靠度方法[14-18]。由于需要利用功能函数在验算点处的Hessian 矩阵，若采用差分法对其计算，尽管改善了计算精度，但降低了计算效率。利用拟牛顿优化方法中对称秩1 方法[13]近似Hessian 矩阵的良好特性[19]，文献[20 - 21]分别将一次可靠度方法的传统优化求解结果或HLRF-BFGS 方法的求解结果与对称秩1 方法的近似Hessian 矩阵计算相结合，给出了与一次可靠度方法具有相同效率的二次可靠度方法。然而，在利用各优化方法获得一次可靠度的结果后，上述方法均主观地将迭代过程的结果直接用于对称秩1 方法中Hessian 矩阵的正迭代，不能保证迭代结果的匹配性；此外，由于引入拉格朗日乘子处理约束优化问题，迭代过程中的Hessian矩阵是针对拉格朗日函数，而非功能函数，因此，严格意义上需通过拉格朗日函数的Hessian 矩阵确定功能函数的Hessian 矩阵。

为此，本文将修正对称秩1 方法[22]与HLRF 法的步长确定策略相结合，发展了一种具有更优收敛性能的改进一次可靠度方法；其次，利用改进一次可靠度方法的迭代结果给出了功能函数的近似Hessian 矩阵，保证了一次可靠度分析与Hessian矩阵近似中参数的匹配性。然后，结合坐标旋转、单变量降维近似模型与非中心卡方分布，提出了可兼顾效率和精度的改进二次可靠度方法。

1 基于修正对称秩1 方法的改进一次可靠度方法

1.1 标准正态空间内可靠度问题的等价描述

式中：ρX为X的相关系数矩阵；μi和σi分别为X的均值和标准差；Herk(·)为Hermite 正交多项式；φ(·)为标准正态变量的概率密度函数；mi为方程的最高次数。表1 给出了三种常用分布的mi，其余常用分布的mi详见文献[23]。

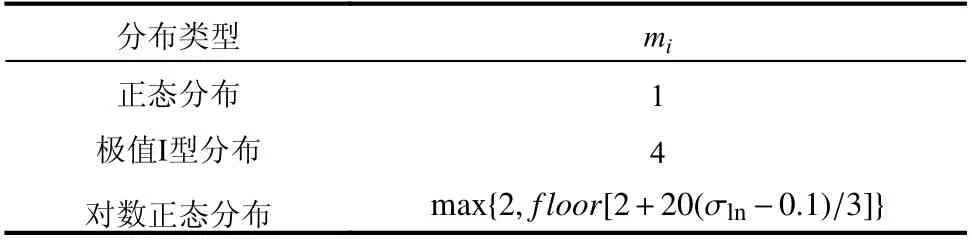
表1 常用分布的miTable 1 mi for common distribution

由上述Nataf 变换，可得标准正态空间的功能函数表达式：

1.2 基于HLRF 法与修正对称秩1 方法的可靠度分析

1.2.1 基于修正对称秩1 方法的可靠度分析

对于式(10)所示的无约束优化问题，可以采用各种优化方法求解。拟牛顿优化方法是一类具有较好收敛性能的优化方法，其中的对称秩1 方法在保持良好收敛特性的同时可以获得较好的近似Hessian 矩阵[19]，修正对称秩1 方法[22]由于在优化迭代过程中更充分地利用了功能函数的函数值与一阶偏导数值，具有比对称秩1 方法和BFGS方法等拟牛顿优化方法更好的收敛性能和计算效率，因此，文中引入修正对称秩1 方法求解上述优化问题。

1.3 隐式功能函数的处理

综合1.1 节～1.3 节，即可形成一种无步长搜索的高效一次可靠度分析方法，本文将其称为基于修正对称秩1 方法的改进一次可靠度方法，简称为改进一次可靠度方法或建议方法1。

1.4 改进一次可靠度方法的实现步骤

文中建议的改进一次可靠度方法的实现步骤为：

1) 计算等效相关系数，将原始空间随机向量X转换为独立标准正态向量U。

2 功能函数的近似Hessian 矩阵及改进二次可靠度方法

功能函数的Hessian 矩阵计算是二次可靠度方法的重要环节。由于在第1 节改进一次可靠度方法的过程中利用了Hessian 矩阵的逆矩阵，尽管该逆矩阵是针对拉格朗日函数的，但仍可能在不增加功能函数调用次数的基础上获得功能函数的Hessian 矩阵近似解。

2.1 基于修正对称秩1 方法的功能函数近似Hessian矩阵

2.1.1 拉格朗日函数的近似Hessian 矩阵

2.2 基于非中心卡方分布积分的改进二次可靠度方法

2.2.1 基于正交矩阵的坐标旋转

为降低二次近似函数中交叉项的影响，一般需采用正交矩阵进行坐标旋转。常用的正交矩阵有：1) 由梯度向量正交化确定的正交矩阵[27]；2) Hessian 矩阵的特征向量矩阵[28]；3) 上述两个矩阵的乘积[20]。考虑到文中Hessian 矩阵是近似确定的，为避免误差累积，故由梯度向量正交化确定的正交矩阵进行旋转。

综合2.1 节和2.2 节，即可形成一种更好地兼顾精度与效率的二次可靠度分析方法，本文将其称为改进二次可靠度方法。

2.3 改进二次可靠度方法的实现步骤

在第1 节改进一次可靠度方法的基础上，改进二次可靠度方法的实现步骤如下：

1) 基于改进一次可靠度方法的计算结果，可根据迭代法(结合式(18)、式(21))或求逆法(结合式(19)、式(21))计算功能函数的近似Hessian 矩阵。

4) 基于式(36)求解失效概率，其中，FZ(·|s,δ)可直接调用MATLAB 软件中的 ncx2cdf(·|s,δ)命令计算。

由于存在迭代法和求逆法两种确定Hessian 矩阵的方式，文中把与之对应的改进二次可靠度方法分别称为建议方法2-1 与建议方法2-2。

3 算例分析

为了验证所提出方法的有效性，文中分别对2 个纯数学表达式的功能函数算例和2 个具有工程背景的算例进行分析。其中，前两者视为功能函数表达式已知的显式功能函数情形，其分析次数为函数调用次数与偏导数计算次数的和；后两者视为功能函数表达式未知的隐式功能函数情形，功能函数的偏导数采用差分法计算，其分析次数为函数调用的次数。同时，为考察建议方法的精度与效率，文中将其与一次可靠度方法中的HLRF法[5]、HLRF-BFGS 方法[12]和二次可靠度方法中的Breitung 方法[14]、拟牛顿近似方法[21]进行对比分析。其中，文献[21]是将近似的Hessian 矩阵与常用的7 种二次可靠度方法分别结合的结果的均值作为最终结果，为简便，本文仅采用其与Breitung方法结合的结果。各方法精度比较时，以抽样数为108的Monte Carlo 法(记为MCS)结果作为标准解，各方法的误差为：

由表3 结果可知，本文建议方法1 相比HLRF法和HLRF-BFGS 方法而言，能够更快收敛，减少了功能函数调用次数，而且达到了近乎相同的一次可靠指标精度，但是上述三种一次可靠度方法的结果精度都不理想。本文建议的改进二次可靠度方法在改进一次可靠度方法的基础上，不额外增加函数调用次数和偏导数计算次数，用更高的效率达到了与二次可靠度方法的Breitung 方法、拟牛顿近似方法相近的精度。值得注意的是，建议方法2-1 与建议方法2-2 的效率与精度完全一致，这验证了本文所提改进二次可靠度方法在一次可靠度分析与Hessian 矩阵近似过程中是自洽的。其余算例在自洽性方面都有相同结论，因此后续算例不再进行讨论。

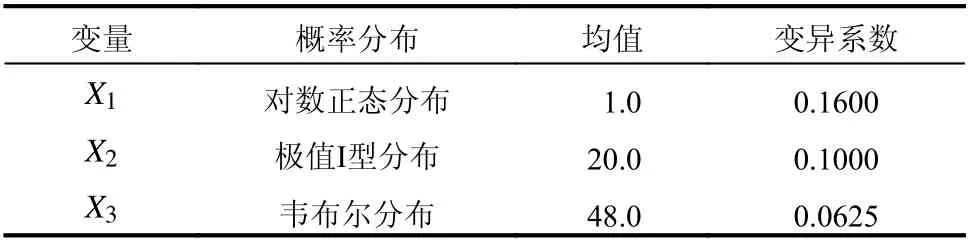
表2 算例1 中随机变量的统计特征Table 2 Statistical characteristics of the random variables in Example 1

表3 算例1 中可靠度计算结果Table 3 computed reliability results of Example 1

算例2. 四变量功能函数

假设功能函数为[28]：

由表4 结果可知，一次可靠度方法中，本文建议方法1 在效率上与HLRF 法、HLRF-BFGS 方法相当，且该三种方法的精度都完全一致，但与MCS 结果相比误差偏大。建议方法2-1 在效率与建议方法1 相同的情况下，提高了可靠指标精度，相比Breitung 方法、拟牛顿近似方法而言误差更小。因此，本文建议的二次可靠度方法能更好地兼顾精度与效率。

表4 算例2 中可靠度计算结果Table 4 computed reliability results of Example 2

由表4 结果可知，一次可靠度方法中，本文建议方法1 在效率上与HLRF 法、HLRF-BFGS 方法相当，且该三种方法的精度都完全一致，但与MCS 结果相比误差偏大。建议方法2-1 在效率与建议方法1 相同的情况下，提高了可靠指标精度，相比Breitung 方法、拟牛顿近似方法而言误差更小。因此，本文建议的二次可靠度方法能更好地兼顾精度与效率。

算例3. 三变量工程实例

考虑Chan 和Low[32]首次提出的一个柔性矩形基础沉降问题，并对其变量类型进行修改，沉降问题的功能函数可以表示为：

假设泊松比与弹性模量之间的相关系数为0.5，部分确定性参数见表5，随机变量统计特征见表6。表7 给出了可靠度计算结果。

表5 确定性参数Table 5 deterministic parameters

表6 算例3 中随机变量的统计特征Table 6 Statistical characteristics of the random variables in Example 3

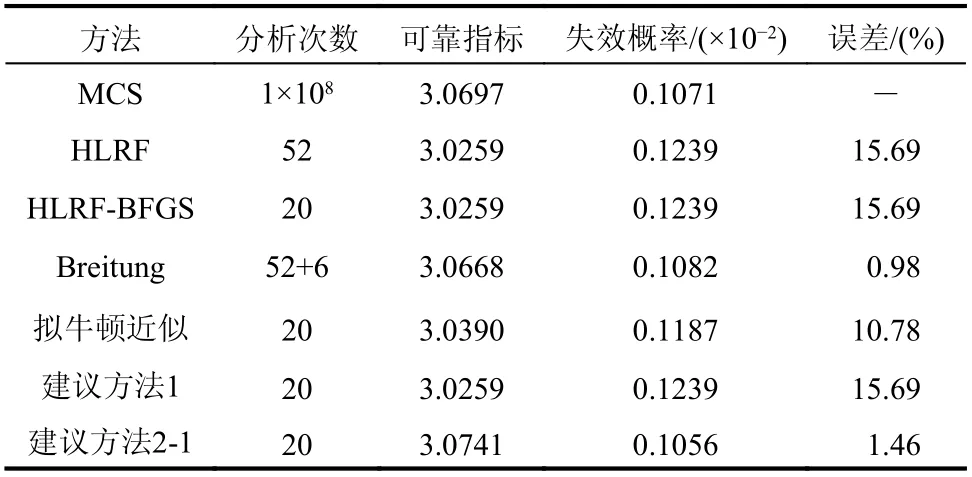
表7 算例3 中可靠度计算结果Table 7 computed reliability results of Example 3

由计算结果可知，一次可靠度方法中，建议方法1 与HLRF-BFGS 方法具有一致的精度与效率，相比HLRF 法具有更高的效率。建议方法2-1相比Breitung 方法而言在保持相近的精度的同时，具有显著的效率提高，与拟牛顿近似方法相比，尽管两种方法效率一致，但建议方法在精度上有明显的改善，进一步验证了本文建议的改进二次可靠度方法在兼顾效率和精度上的优势。

算例4. 多变量工程问题

考虑文献[33]的具有9 个随机变量的悬臂管工程算例，如图1 所示，悬臂管在x-y平面上受集中荷载F1、F2，在y-z平面受轴力P与扭矩T，图1中的A点将出现最大的Von-Mises 应力σmax，将σmax超过材料的屈服强度Sy作为失效准则，于是功能函数为：

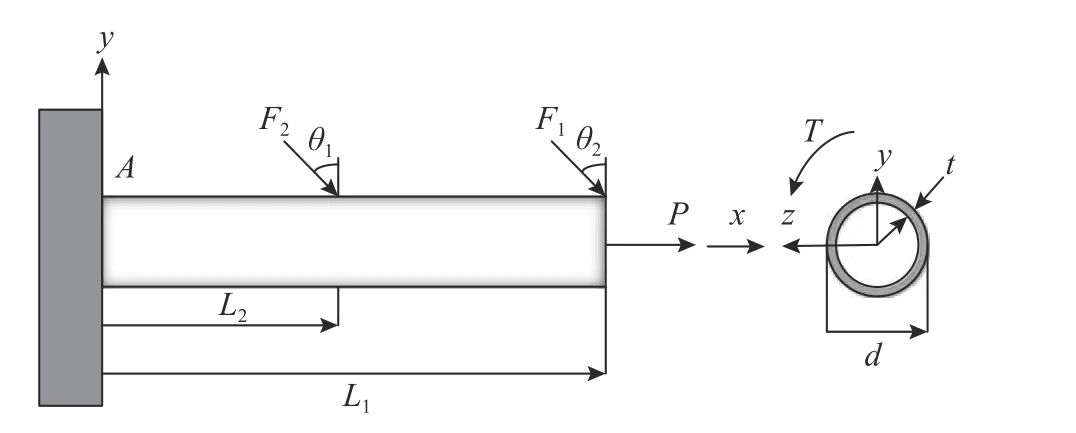
图1 悬臂管Fig. 1 Cantilever tube

算例中两个角度为定值，θ1=5o、θ2=10o。悬臂管随机变量统计特征见表8，其中，原文献中可靠指标偏低，文中对屈服强度参数进行调整以达到高可靠指标。表9 给出了可靠度计算结果。

表8 算例4 中随机变量的统计特征Table 8 Statistical characteristics of the random variables in Example 4

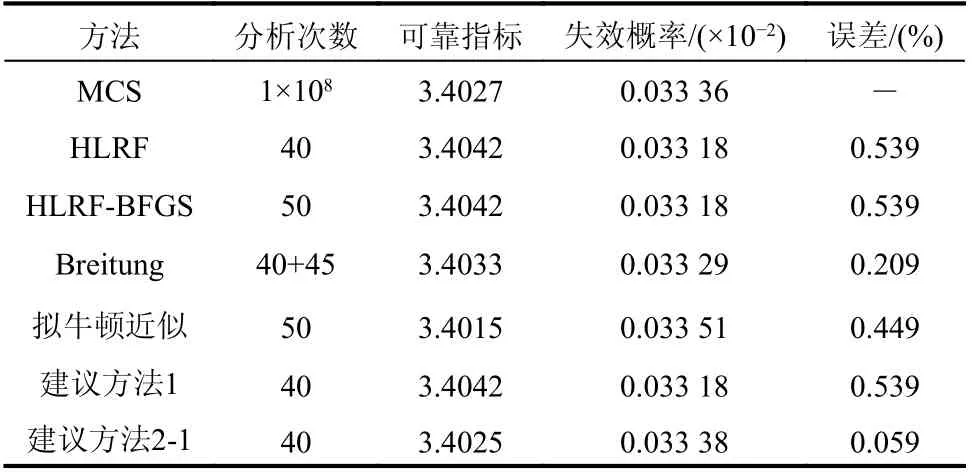
表9 算例4 中可靠度计算结果Table 9 computed reliability results of Example 4

可以看出，本文建议方法1 与HLRF 法在效率和精度上都一致，相比HLRF-BFGS 方法而言收敛更快。建议方法2-1 在效率和精度上，相比已有的二次可靠度方法都有一定改善。

4 结论

本文引入拉格朗日乘子，将约束优化的可靠度问题转化为无约束优化问题，并结合修正对称秩1 方法与HLRF 法，提出了具有较好收敛性的改进一次可靠度方法。在此基础上，结合坐标旋转、单变量降维近似和非中心卡方分布进一步提出了改进二次可靠度方法。通过算例分析可得到如下结论：

(1)由于修正对称秩1 方法的良好收敛特性和HLRF 法无需迭代确定步长的特点，本文的改进一次可靠度方法继承了两者的优点，既有良好的收敛性，亦有较高的效率。

(2)由于近似的Hessian 矩阵既可以基于改进一次可靠度方法的迭代过程结果确定，亦可以由最终的Hessian 逆矩阵求逆获得，且能保持两者结果的一致性，因此，本文的改进二次可靠度方法在一次可靠度分析与Hessian 矩阵近似过程中是自洽的。

(3)由于改进二次可靠度方法所采用的Hessian矩阵不需要额外调用功能函数，因此，本文的改进二次可靠度方法可以更好地兼顾效率与精度。

(4)由于引入差分近似偏导数，本文的建议方法均适用于显式、隐式功能函数。