高光谱遥感影像降维：进展、挑战与展望

苏红军

河海大学 地球科学与工程学院,南京 211100

高光谱遥感技术作为遥感科学的新兴方向之一，具有光谱分辨率高、特征维数高、信息冗余、图谱合一等优势（童庆禧等，2006）；近年来在国土监测、农林调查、灾害预警、生态环境评估、军事国防等领域得到了广泛应用（浦瑞良和宫鹏，2000；张良培 等，2011；张兵，2011b；甘甫平等，2014）。高光谱遥感的应用需求要求对其数据能够快速有效处理（杜培军 等，2012；Chang，2013）。现有方法在处理高光谱遥感影像的高维数据时算法复杂度较高，且数据冗余和相关性降低了算法性能，同时会遇到Hughes 现象（Hughes，1968）：即在样本数一定的情况下，随着特征维数的增大，分类精度会出现“先增后降”的现象。小样本情况下，为了在样本数目、数据维数和分类精度之间取得平衡，高光谱遥感影像的降维处理成为后续数据处理与分析的必要环节之一。

高光谱遥感影像降维是在尽可能地保留有效信息或特征的同时，利用特征提取或波段选择等方法，对高光谱遥感影像数据进行高效、精准处理，主要方法可归纳为以下两类（Chang，2013；张良培和张立福，2011；Jia 等，2013；张兵，2016）：（1）特征提取，即对高光谱遥感影像所有波段进行数学变换，提取对后续应用最为有效的特征；（2）特征选择，即从高光谱遥感影像所有波段中选择对后续分析最有效的波段。由于高光谱遥感影像数据的特殊性，虽然现有研究取得了较大进展，但是依然面临许多问题，需要机器学习、模式识别等领域相关理论和方法的支持。

本文在分析高光谱遥感影像降维必要性的基础上，对高光谱遥感影像降维的若干方法和最新进展进行了综述，分析了当前高光谱遥感影像降维面临的挑战，并对其热点问题进行探讨，最后给出了结论和展望。

1 高光谱遥感影像降维的必要性

1.1 信息分布特征

高光谱遥感影像数据可看成图像立方体（图1（a）），包含了3 种表达模式：即图像空间（反映光谱响应与地物位置关系）、光谱空间（反映光谱响应与地物类型关系）、特征空间（图1（b）—（d）），实现了高光谱遥感数据图像维、光谱维和特征维的有机结合。

图1 HYDICE WASHINGTON DC 数据示意图Fig.1 The data diagram of HYDICE WASHINGTON DC

高光谱遥感影像数据的特点导致其信息在特征空间中的分布不同于其他数据（Landgrebe，1998）：高维特征空间中样本的分布是稀疏的、高维数据的线性投影遵循正态分布特性、分类时所需的训练样本随维数的增加而增加、高维数据中存在大量数据冗余等。以下从数据冗余的角度，分析高光谱遥感影像数据的空谱特性：（1）空间相关性，即影像某像元与其相邻像元间存在相似性，可用相关函数描述；图2 和图3 展示了空间相关性，该指标在一定程度上反映了不同地物类型的空间分布。（2）谱间相关性，即相邻波段间同一地物像元的相关性；由图4可知相邻波段间像元的相关性非常大（需要说明的是，图4（b）第100波段和第135波段附近出现了异常弱相关现象，这是因为删除了部分水吸收和噪声波段，100 和135 附近的波段在原始数据中并不是邻近波段，所以其相关性较弱）。（3）空谱相关性，即空间和谱间的整体相关性；图5展示了空谱相关性结果，计算时像素偏移设置为30，波段偏移设置为191；如图5（a）所示，除第3、4 和6 行的部分矩阵值小于0.9 外，图5 中其他大部分值在0.9 以上；可见，高光谱遥感影像的空谱相关性比较强。

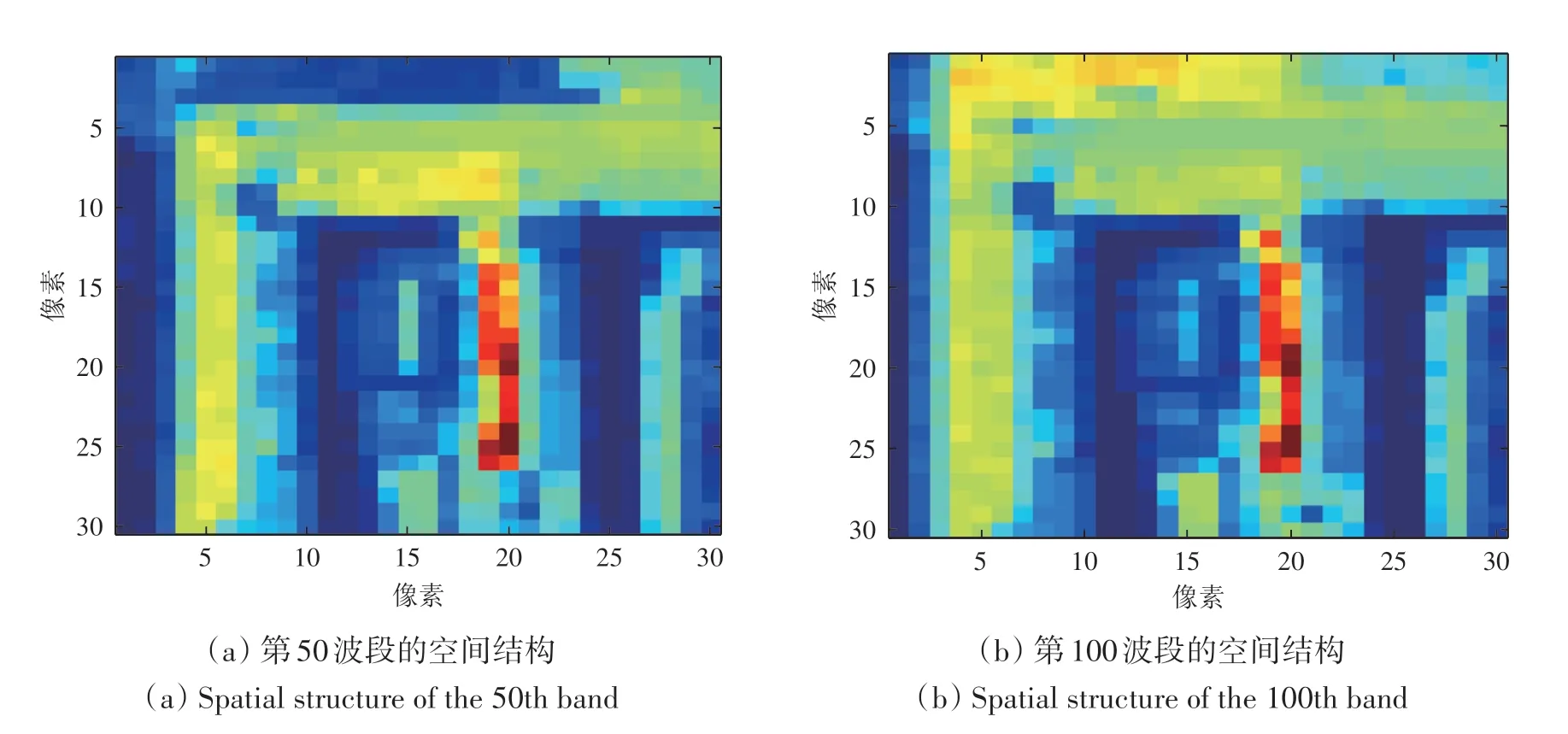
图2 HYDICE WASHINGTON DC 数据第50与100波段的局部空间结构Fig.2 The local spatial structure of the 50th band and the 100th band in HYDICE WASHINGTON DC data

图3 HYDICE WASHINGTON DC 数据空间相关性Fig.3 The spatial correlation of HYDICE WASHINGTON DC data

图4 HYDICE WASHINGTON DC 数据谱间相关性Fig.4 The correlation of HYDICE WASHINGTON DC data spectrum

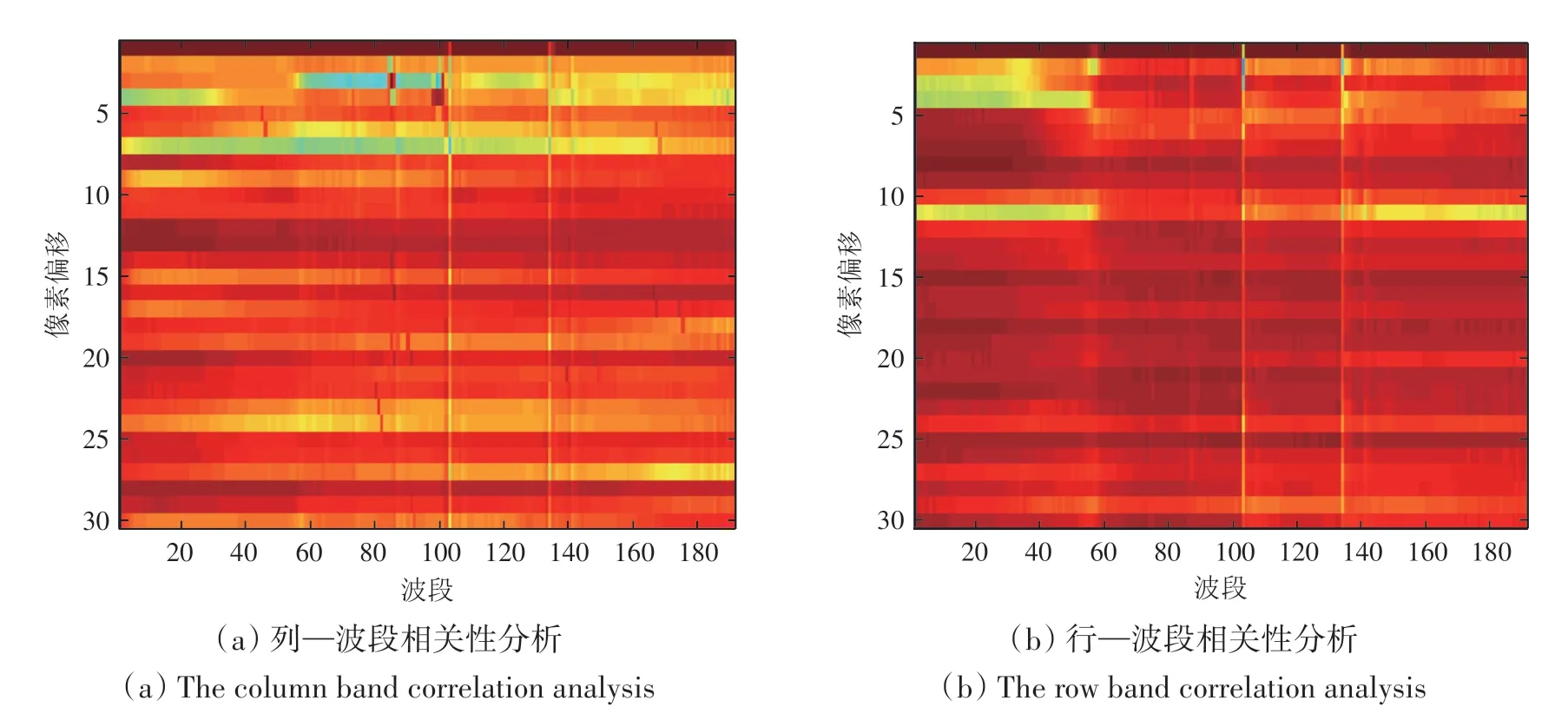
图5 HYDICE WASHINGTON DC 数据空谱相关性Fig.5 The spatial spectral correlation of HYDICE WASHINGTON DC data

需要说明的是，高光谱遥感的像素值有DN 值和反射率等两种：DN 值由于受传感器、大气、地形和高度角等因素的影响，并不能真正反映地物的灰度值；反射率数据是利用辐射传播模型等去除

了云层、大气组分、周围地物的影响，得到的地表的反射率数据。因此，反射率数据对光谱特征的表达更为有效。

综上，（1）高光谱遥感影像信息分布的稀疏性使得可用低维空间近似表达高维空间，这就是高光谱遥感影像降维的理论基础；（2）高光谱遥感影像数据的相似性使得有可能对其有效信息进行挖掘，高光谱遥感影像降维具有可行性；（3）高光谱遥感影像分类受制于小样本等问题，也突显了其降维的必要性。

1.2 维数灾难与Hughes现象

由上述分析可知，高光谱遥感影像数据具有高维特征、信息冗余、小样本等特点，因而在数据处理过程中会遇到维数灾难问题（Curse of Dimensionality）（Bellman，1961）：即由于维数增加而导致的计算量急剧增长以及预测模型的过拟合等问题。其原因在于训练样本在高维特征空间中的分布非常稀疏，从而导致分类器参数估计困难，进而出现过拟合现象。因此，减少特征维数可以在某种程度上消弱“维数灾难”的影响。

另一方面，对于分类器模型来说，维数的增加必然导致训练样本需求数量的快速增加，但在高光谱遥感场景中，训练样本的获取费时费力，其数目是有限的。研究发现，特征维数、样本数目与分类精度之间存在着较为复杂的关系：即在样本一定的情况下，随着特征维数的增大，分类精度会出现“先增后降”的现象，如图6所示，即著名的Hughes现象（Hughes，1968）。

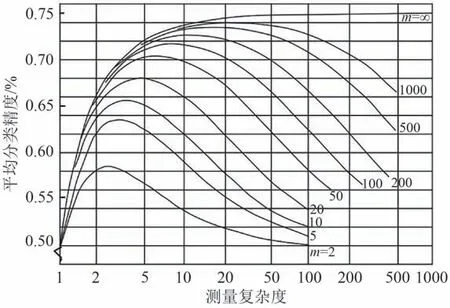
图6 特征维数、样本数目和分类精度的关系（Hughes，1968）Fig.6 The relationship among sample number，dimension and classification accuracy（Hughes，1968）

需要注意的是，很多研究往往把维数灾难与Hughes 现象相混淆，其实，两者的关注点是不同的，维数灾难强调高维数据下信息分布急剧变化所导致的问题，而Hughes 现象则强调训练样本、特征维数对分类精度的影响问题。由维数灾难与Hughes 现象可知，小样本情况下的影像降维可有效提升高光谱遥感的分类精度。

可见，高光谱遥感影像降维具有可行性和必要性，但是高光谱遥感影像降维并不是遥感影像处理过程中必需的一个过程，在具体应用中应根据不同应用的实际需求，选择是否进行降维处理。

2 高光谱遥感影像降维研究进展

利用高光谱遥感的原始数据进行分类时不但数据量大、样本少，且会面临Hughes 现象；为了在样本数目、特征维数、分类精度、处理效率之间取得平衡，高光谱遥感影像降维十分必要。本文主要从特征提取、特征（波段）选择两方面对高光谱遥感影像降维的研究进展进行分析。

2.1 特征提取研究进展

特征提取通过一定的数学模式将影像数据从高维空间映射到低维空间，降维后的特征可在一定程度上保留原始数据尽可能多的重要信息。其主要方法可归纳为：基于指数/参数的特征提取、基于投影/转换理论的特征提取、基于波段组合的特征提取、基于空间域算法的特征提取、基于流形学习的特征提取和基于深度学习的特征提取等（表1）。

表1 高光谱遥感特征提取算法体系Table1 Feature extraction algorithm system for hyperspectral remote sensing

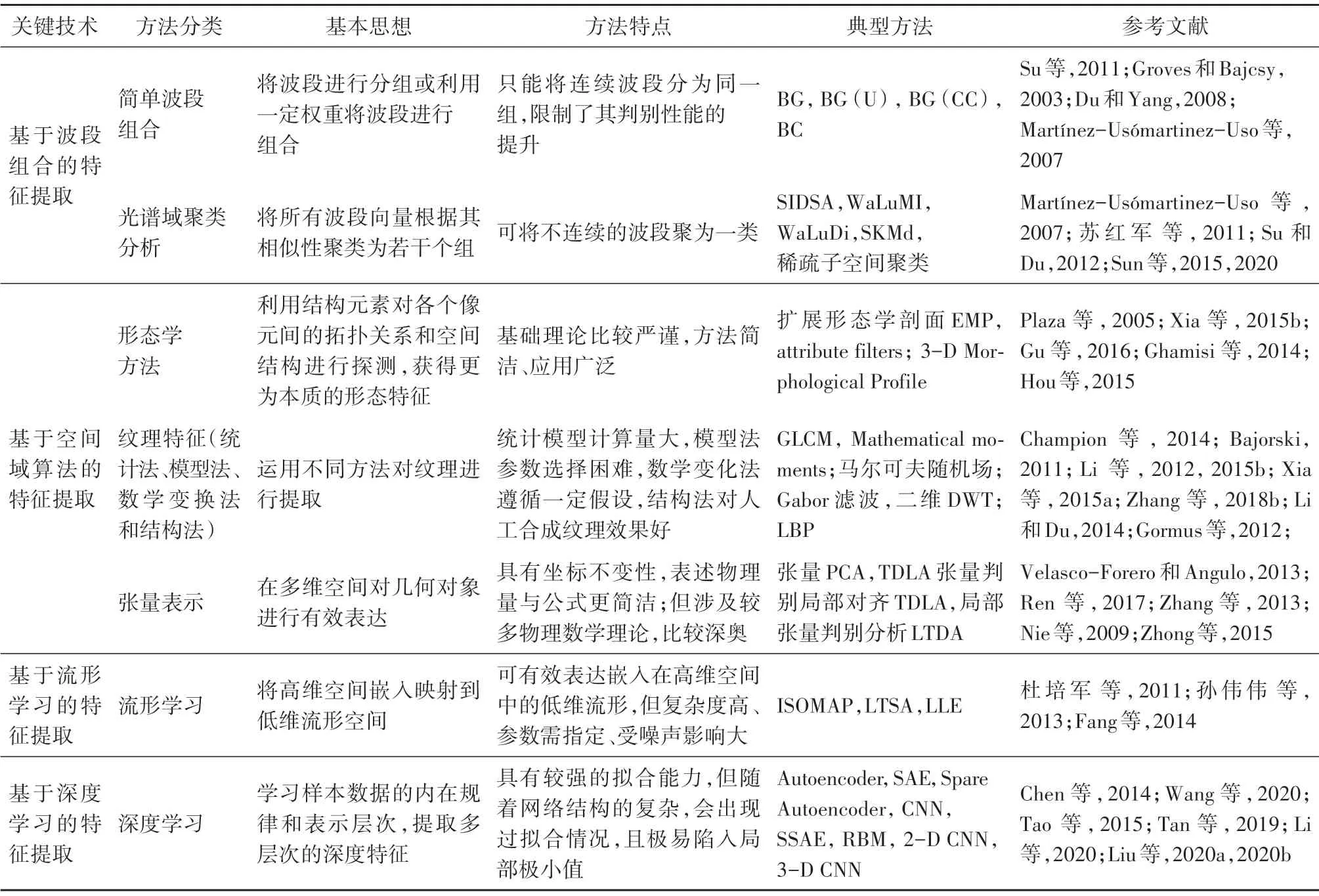
续表

2.1.1 基于指数/参数的特征提取

根据电磁波理论，不同物质由于其化学成分、分子结构、表面状态等差异，在某些波段上具有独特的具有诊断意义的典型光谱吸收特征，根据吸收特征可以对物质进行精准识别。吸收特征具有明显的物理意义，如水吸收特征、叶绿素吸收特征、某些气体的吸收特征，以及矿物吸收特征等。如基于指数的方法主要结合地物的光谱特征，对若干波段进行数学运算，其目的是通过波段运算突出光谱波段的某些特征，即地物类别的光谱知识。例如应用广泛的遥感指数：归一化植被指数（NDVI）（基于叶绿素吸收特征）（Haboudane等，2004）、叶面积指数（LAI）（基于水吸收特征和NDVI）（Fang 和Liang，2008）、归一化水体指数（NDWI）（Gao，1996）、土壤调节植被指数（SAVI）（Huete，1988）、归一化建筑指数（NDBI）（Zha 等，2003）、遥感生态环境指数（RSEI）（徐涵秋，2013）等。以上特征提取方法建立了提取特征与地表物理参数的直接关联，但是在特征运算的过程中却需要领域专家的参与（也称为基于知识的特征提取）。

从本质上讲，基于知识的特征提取类似于特征挖掘，即利用算法指标从原始光谱数据中提取出不同于原始光谱数据的信息，提取的信息可用于区分不同的地物类型和目标。一般在特征提取前需对光谱曲线吸收特征进行处理，其算法可归纳为以下两类：（1）光谱特征增强方法，即利用某种算法对原始光谱曲线进行数据预处理，以达到增强光谱吸收特征的目的；如连续统去除法（Continuum removal）（Filippi和Jensen，2007）、光谱微分技术（Spectral derivative analysis）（Debba 等，2006）、尺度—空间算法（Scale-space algorithms）（Piech和Piech，1987；Hsu，2007）等。连续统去除法是对光谱曲线数据进行归一化处理，并在忽略总体反射率的情况下突出特定吸收特征的位置和深度。光谱微分技术是对光谱数据曲线求导，以便突出其吸收特征；二阶微分所揭示的吸收波段比一阶微分范围更宽，但是微分技术受噪声的影响较大。尺度—空间算法即从不同的尺度上分析光谱曲线，对吸收特征从尺度—空间表达上进行适当的操作处理；该方法既能从大尺度上鉴别吸收特征，也能从精细尺度上定位吸收特征位置。（2）光谱特征建模方法，即在对光谱特征进行分析和高度抽象的基础上构建相应数学模型的方法，如改进高斯模型MGM（Modified Gaussian Modeling）（Sunshine等，1990）和光谱特征参数（王晋年等，1996；van der Meer，2004；Guo，2020）等方法。其中改进高斯模型方法假定光谱吸收特征的能量是随机分布的，可利用幂定律描述能量和平均键长的关系，并以此描述该光谱的吸收特征，进而可根据估计参数值对光谱吸收特征进行建模；由于通常情况下，一个光谱曲线一般包含多个吸收特征，因此，对每个光谱吸收特征都需建立其改正高斯模型。光谱特征参数方法则利用诸多参数（如吸收波长位置、宽度、深度、斜率等）对光谱吸收特征进行描述，也可以根据相关参数建立光谱吸收指数。该类方法所提取的参数较多，使用较不方便。

2.1.2 基于投影/转换理论的特征提取

基于知识的特征提取需要专家经验的支持，然而，应用中很难获取较为理想的专家知识；因此可以直接对数据进行统计分析，即基于统计理论的特征提取方法，该类方法是在不损失有效信息的条件下，将高维数据变换到低维空间，从而突出类别的可分性，该算法的难点是如何构建理想的变换矩阵。根据是否利用先验知识，基于统计理论的特征提取方法可分为以下几类。

（1）非监督特征提取。该类方法对高光谱遥感数据直接进行处理，无需利用训练样本数据。主要包括数学变换和信号分离等方法。数学变换方法即利用变换矩阵将影像数据从高维空间映射到低维空间；目前应用到高光谱遥感领域的主要方法有投影追踪PP（Projection Pursuit）（Ifarraguerri和Chang，2000）、主成分分析PCA （Principal Component Analysis）（Chang，2013）、噪声调整的主成分变换NAPC（Noise-Adjusted Principal Component）（Chang 和Du，1999）、基于分割的PCA 技术（Jia和Richards，1999；Du 等，2009）等；基于PCA的算法假设信息变量之间存在较大的方差，取决于数据的二阶统计量，信息较大的主成分具有较低的信噪比；在使用PCA 之前，如果不同维度数据的变化幅度较大或者不属于同一量纲，可以对数据首先进行归一化处理（去均值后除以数据的标准差，或者直接除以数据绝对值的最大值）；为进一步降低影像中相邻像元之间的相关性，可对数据进行白化处理（把各个特征轴上的数据除以对应特征值）。然而，图像质量有时并不一定随着主成分的减少而逐步下降，基于方差的主成分有时并不一定能充分表征图像质量。为克服以上问题，提出了最大噪声分数变换MNF（Maximum Noise Fraction）并应用到高光谱遥感特征提取领域（Dadon 等，2010；Dopido 等，2012）；张 兵 等（2004）基于凸面几何体投影变换利用高光谱遥感影像进行目标探测研究。PCA 和MNF 方法均基于数据的二阶统计量，都不能有效地描述细微地物的特征，因为方差矩阵的精准估计建立在大量充足的样本之上，而细微地物的样本不足无法构成可靠的统计。

针对以上问题，基于信号分离的方法如独立成分分析ICA （Independent Component Analysis）（Wang 和Chang，2006）可取得较好的特征提取效果；该方法从盲源分离角度将高光谱遥感数据按照统计独立原则分解为独立分量，最后实现高效的特征提取（Mura 等，2011；Falco 等，2014）。以上算法虽能取得较好的特征提取效果，但均无法对复杂数据中的非线性关系进行建模；因此，又发展了系列基于核技术的方法，即利用核函数技巧对参数进行有效估计，如PCA、MNF 和ICA均发展了核版本算法，即KPCA（Gu 等，2008；Xia 等，2017）和KICA（Shen 等，2009）等，可得到较好的特征提取效果，但受核函数的影响较大。

（2）监督特征提取。该类方法需要利用高光谱遥感数据的训练样本等先验知识，根据数据的分布形式是否已知，可分为参数型和非参数型等两类。参数型方法假设数据遵循由某些参数确定的分布模型；如线性判别分析LDA （Linear Discriminant Analysis）（Li等，2011）、局部费舍尔判别分析LFDA（Local Fisher’s Discriminant Analysis）和典型相关分析CA（Canonical Analysis）等方法就是基于每一类的均值向量和协方差矩阵、类别可分性等，利用类内与类间散度矩阵的比值构建方法模型（Richards和Jia，2006；Zhang和Prasad，2015）。然而，LDA 的性能依赖于类别数据的高斯分布，难以处理分布比较复杂的类别数据；而且，小样本情况下，对高维数据进行分类时，类内散度矩阵容易出现奇异值现象（Kuo 和Landgrebe，2004）；当训练样本的数目与数据的维数相当时，二阶统计值的估计在类别层次上往往是不可靠的。

非参数型方法则可以克服参数型方法存在的问题，该类方法对数据分布不做任何假设，既不知分布的具体形式，也不知分布的具体参数。如非参数判别分析NDA（Nonparametric Discriminant Analysis）（Kuo 等，2009）通过寻找对特征有贡献的类别样本定义非参数类间散射矩阵，避免了参数型方法的问题，但是存在奇异值问题；非参数权重特征提取NWFE（Nonparametric Weighted FE）（Kuo 等，2009）通过定义新的类内和类间散度矩阵计算权重均值，取得了比LDA 和NDA 更好的分类效果，但是该方法的计算时间过长，且仍然存在奇异值问题。基于余弦的非参数特征提取CNFE（Cosine-based Nonparametric Feature Extraction） 则利用基于余弦距离的权重函数计算散度矩阵，采用正则化技术解决了奇异值问题（Yang 等，2010）。而决策边界特征提取DBFE （Decision Boundary Feature Extraction）利用决策边界代替类均值和方差矩阵，寻求一个正交于类别决策边界的新特征（Benediktsson 等，1995），可在一定程度上缓解奇异值问题。针对高光谱遥感影像分类的小样本问题，在设计特征提取算法时，类内和类间散射矩阵、正则化技术和特征值分解是解决小样本问题SSS（Small Sample Size）的重要方法（Kuo 和Landgrebe，2004；Kuo等，2009）。另外，近年来，在核技术的支持下，出现了一些核空间非线性特征提取方法，类别可分性在核空间内得到了提升；如核局部费舍尔判别分析KLFDA （Kernel local FDA）（Li 等，2011）和泛化判别分析GDA（Generalized Discriminant Analysis）（Baudat 和Anouar，2000）等方法。

（3）半监督特征提取。当标签样本数据较少时，所提取特征的判别能力也较低。近年来，相关研究开始关注如何充分利用样本数据和无标签数据的信息，该类方法即半监督特征提取。主要方法有成对约束方法（Chen 和Zhang，2011）、半监督核偏最小二乘法（Izquierdo-Verdiguier 等，2014）、半监督局部判别分析（Liao等，2013）、半监督流形判别分析（Luo 等，2016）和半监督协同标签传播（Zhang 等，2020）等。半监督学习一般依赖于3个基本假设，即平滑假设、低密度假设和流形假设，即邻近的像元具有相似的性质；但是以上假设比较简单，没有考虑噪声对样本的干扰。

需要说明的是，所提取的特征可能有多种类型，比如光谱波段（DN 值）、光谱波段（反射率）、PCA变换主成分、卷积网络的特征图等。DN值由于受外界因素的影响，其效果不佳；而反射率则去除了外界的影响，反应了地表的反射率，其特征数据较为有效；PCA 主成分实际上是变换后特征空间中的特征，去除了相关性和噪声影响，一般前3个主成分就能包含99%以上的信息量；卷积网络的特征图是由卷积核提取的特征，对特征图进行卷积，特征之间继续组合，可以获得更复杂的特征图。因此，实际应用中，需考虑所选择特征的类型信息。

2.1.3 基于波段组合的特征提取

高光谱遥感具有数百个波段，相邻波段间的信息较为冗余，可以将在某一光谱范围内的波段分为一组，从而降低数据维数，提取有效特征。另外，不相邻的波段也可能具有一定的相似性，因此也可对光谱域进行聚类分析，将不相邻的相似波段聚为一类，从而提取有效特征。

（1）简单波段组合。最简单的是对波段分组BG（Band Grouping）或利用一定的权重将波段进行组合（Su 等，2011），如将波段进行均等分组BG（U）（Band Grouping Uniformly）（Groves和Bajcsy，2003）或依据一定的相关性分组BG（CC）（Band grouping by spectral correlation coefficient）等方法（Du 和Yang，2008）等。但是，该类方法如BG（CC）和BG（U）等仅能将相邻波段分为一组，限制了其判别性能的提升。

（2）光谱域聚类分析。该类方法首先将每个波段转化为一个向量，然后将所有的波段向量根据其相似性聚类为若干组，每组中包含了若干相似性比较大的波段，这些波段具有类似的性质和特征，从而间接实现高光谱遥感数据的波段分组。如基于聚类的波段组合方法BC（Band Clustering）如SIDSA、WaLuMI、WaLuDi等（Martínez-Usómartinez-Uso 等，2007），基于K-均值及其改进算法的波段聚类和选择方法SKMd（Su 等，2011；Su 和Du，2012），以及基于稀疏子空间聚类方法（Sun 等，2015，2020）等。基于聚类的降维由于能将不相邻的波段聚为一组，具有更高的性能和鉴别能力。

2.1.4 基于空间域算法的特征提取

光谱特征在高光谱遥感信息处理中发挥了重要作用，但仅仅依靠光谱数据往往不一定能达到较好的分类效果，空间特征的加入可进一步提升高光谱遥感信息处理的性能，已成为一个新的研究热点；因此，充分挖掘高光谱遥感影像数据中的多种空间特征（如纹理、上下文等），对于提升高光谱遥感影像处理的可靠性、稳定性具有重要意义。本文主要对形态学特征提取、纹理特征提取和张量空间特征提取等方法进行综述。

（1）形态学特征提取。该类方法主要涉及集合和拓扑、几何形状和结构等内容，已成为遥感图像处理领域的热点方法（Plaza等，2005）。该方法利用结构元素（structure element）对影像中各个像元间的拓扑关系和空间结构信息进行探测，可获得地物更为本质的形态特征；该算法主要由若干代数算子组成，其基本运算主要有膨胀（dilation）和腐蚀（erosion），以及由二者组合得到的开运算（open）和闭运算（close）。目前，在高光谱遥感特征提取中应用广泛，如利用扩展形态学剖面EMP （Extended Morphological Profile）（Plaza 等，2005；Xia 等，2015b；Gu 等，2016）、属性滤波（attribute filters）（Ghamisi 等，2014）、3-D Morphological Profile（Hou 等，2015）等方法对高光谱遥感影像的空间特征进行提取。形态学的基础理论比较严谨，方法简洁、应用广泛。

（2）纹理特征提取。高光谱遥感影像纹理作为影像空间中地物特征空间分布的一种描述，对后续分析具有重要价值。目前的纹理特征提取方法可归纳为以下几种：（1）统计分析方法，研究纹理区域中像元及其邻域属性的统计特征，如灰度共生矩阵GLCM（Gray Level Co-occurrence Matrix）（Champion等，2014）、数学矩（Mathematical moments）（Bajorski，2011）等方法，GLCM 纹理特征鉴别性能较好，但是计算复杂；（2）模型分析方法，基于统计或信息理论对纹理基元分布进行数学建模，通过设定不同的模型参数来定义不同的纹理，如马尔可夫随机场（Li等，2012；Xia等，2015a；Zhang等，2018b）等，其困难在于如何选择合适的参数；（3）频谱变换法，即利用数学变换将空间域的纹理图像投影到频率域，获得在空间域不易获取的纹理特征，如Gabor 滤波（Li 和Du，2014）、3D-Gabor（Jia等，2018）、二维DWT（Gormus等，2012）等方法；（4）结构分析方法，对由一定排列规则的纹理基元构成的纹理进行建模，如局部二值模式LBP （Local Binary Pattern）（Li 等，2015b）等，该类方法能够很好地识别人工纹理。

（3）张量空间特征提取。传统的特征提取模型大多基于高光谱遥感影像的向量空间，因需要将三维的高光谱遥感影像转换为二维形式，会破坏高光谱影像的空间邻域信息。而张量作为不随坐标系改变而改变的某种几何对象，可在多维空间对几何对象进行有效表达，具有坐标不变性。近年来，基于张量的方法得到快速发展，已广泛应用于遥感影像分类、目标探测等领域，高光谱遥感影像的张量表示（tensor representation）同时保留了空间维度和波段信息，使用该方法可以提取空谱联合特征。大部分基于张量表示的方法基本上都是从传统基于向量的方法扩展而来的，如张量主成分分析（Tensor PCA）（Velasco-Forero 和Angulo，2013；Ren等，2017）方法、张量判别局部对齐TDLA（Tensor Discriminative Locality Alignment）（Zhang 等，2013）、局部张量判别分析LTDA（Local Tensor Discriminant Analysis）（Nie 等，2009；Zhong 等，2015）等方法，均能够有效挖掘高光谱遥感影像的空谱特征。张量方法表述物理量与公式时更加简洁、更形象生动、优雅内蕴，但是该类方法涉及较多物理和数学理论，比较难以理解。

2.1.5 基于流形学习的特征提取

高维数据在特征空间上对应的点往往分布在“低维流形”上，找到各个点在“低维流形”上的坐标，即可实现基于流形学习的降维。当前国内外对流形学习进行了诸多研究，如全局化等距映射（ISOMAP）（杜培军等，2011）、等距映射和局部切空间排列LTSA（Local Tangent Space Alignment）（孙伟伟等， 2013）、 球形随机近邻嵌入（Spherical Stochastic Neighbor Embedding）（Lunga和Ersoy，2013）、融合空间信息的局部线性嵌入方法LLE （Locally Linear Embedding）（Fang 等，2014）、非监督加权空—谱联合保持嵌入（WSCPE）（黄鸿等，2019）、空谱邻近流形对齐算法（Yang和Crawford，2016）等。流形学习目前存在的问题是算法复杂度较高、参数需事先指定或人为设定，且受噪声的影响较大。

2.1.6 基于深度学习的特征提取

经典的特征提取方法不能很好地表达高光谱遥感影像的非线性特征，其应用受到了限制。近年来，深度学习算法由于对非线性数据处理的优越性，在高光谱遥感影像处理领域得到了广泛应用。深度学习采用多层次学习框架，利用深度神经网络提取多层次的深度特征（如低层纹理特征，中层特征，高层特征等），进而有效表达数据特性。相关算法已应用于高光谱遥感影像光谱特征提取，如自编码器AE（Autoencoder）（Chen 等，2014）、堆叠自编码器SAE（Stacked autoencoder）（Wang等，2020）、稀疏自编码器（Spare autoencoder）（Tao 等，2015）、受限玻尔兹曼机RBM（Restricted Boltzman Machine）（Tan 等，2019）和卷积神经网络CNN （Convolutional Neural Network）（Li 等，2020）等方法。另外，也发展了一些能够提取空间特征和空谱特征的方法，如堆叠稀疏自编码器SSAE（Sparse stacked autoencoder）（Tao 等，2015；Liu等，2020b）、2-D CNN（Wang 等，2019）和3-D CNN（Liu等，2020a）等。深度学习特征提取算法的网络结构复杂，具有较强的拟合能力，可以逼近较为复杂的函数；但是会出现过拟合现象，且会陷入局部极小值。

2.2 特征选择研究进展

特征提取主要是利用数学模型将原始高维的波段数据映射为对后续应用较为有效的低维特征，其难点在于构建合理的变换矩阵，且由于数据失去了原始的物理意义，无法与样本数据建立可靠关联，存在一定缺陷。特征（波段）选择则是从高光谱遥感影像的所有原始波段中挑选出针对后续应用最有效的波段子集，并可有效保留原始波段数据的物理特性，得到了广泛应用。波段选择一般需要解决3个关键技术难题：（1）定义何种信息测度指标作为目标函数，（2）采用何种搜索优化策略提升算法效率，（3）确定合理的波段选择数目。本文主要从信息测度、搜索优化策略、最优波段数目、多特征质量评估和多特征优化等方面进行综述（表2）。

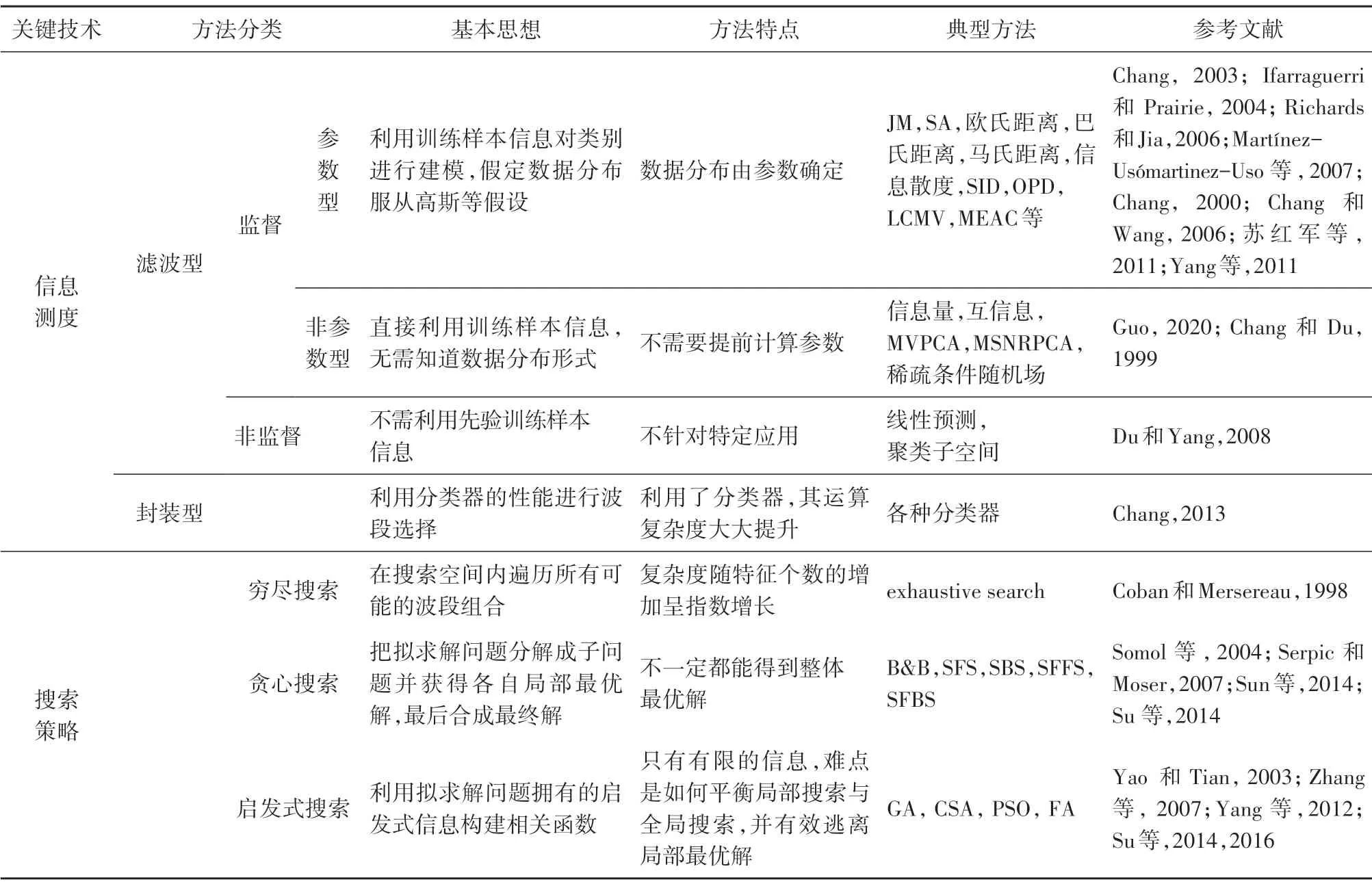
表2 高光谱遥感波段选择算法体系Table 2 Band selection algorithm system for hyperspectral remote sensing

续表

2.2.1 信息测度

波段选择选出的波段应满足信息量尽可能大、相关性尽可能小、可分性尽可能强等原则。最初提出的波段选择算法基本上是在保留最大信息的前提下基于某种信息测度准则选择某些波段，该方法由于删除了大部分波段，极易造成信息的丢失，可见信息测度的选择至关重要。按照采用的信息测度的不同，可以将其分为采用信息测度为目标函数的滤波器型波段选择方法（Filter approach），以及采用分类器性能为准则的封装型波段选择方法（Wrapper approach）（Chang，2013）等两类；其中，滤波器型方法简洁高效，应用较为广泛；而封装型方法由于嵌套了分类器，其运算复杂度较高，应用较少。根据是否利用样本知识，滤波型波段选择方法可分为监督和非监督等两类。

第一类为监督滤波型波段选择方法。该类方法主要利用地物类别的判别信息构建信息测度函数，面向应用选择出能反映类别光谱特征的波段。其中样本数据即是最重要的先验知识，依据样本信息利用的程度，可以将监督波段选择方法分为两种：

（1）参数型方法。该类方法主要利用有标签样本对地物进行建模，如常用的JM距离JM（Jeffries-Matusita distance）（Chang，2003；Ifarraguerri 和Prairie，2004；Richards 和Jia，2006）即为参数型信息测度方法，该方法建立在数据分布服从高斯假设的基础上，并对类别信息进行建模，得到类别均值和协方差矩阵，进而衡量不同波段的距离进行波段选择。另外，光谱角SA （Spectral Angle）、欧氏距离（Euclidean distance）、马氏距离（Mahalanobis distance）、巴氏距离（Ifarraguerri 和Prairie，2004）、信息散度（Divergence）（Martínez-Usómartinez-Uso 等，2007）、光谱信息散度SID（Spectral Information Divergence）（Chang，2000）、正交投影散度OPD（Orthogonal Projection Divergence）（苏红军 等，2011）、线性约束最小方差LCMV（Linearly Constrained Minimum Variance）（Chang 和Wang，2006）、形态学膨胀距离（Dilation Distance）（Challa 等，2022）等波段选择方法也得到了广泛应用。以上距离函数类别分离性也可以根据类内方差和类间方差的比率确定，如利用能刻画出最佳端元的类别均值，构建了基于最小估计丰度方差MEAC（Minimum Estimated Abundance Covariance）（Yang 等，2011） 的波段选择方法，得到广泛应用。

（2）非参数型方法。该类方法直接利用有标签样本进行分析。如利用相关性测度对冗余波段进行删除、利用类别间的信息量进行波段选择的方法等。目前信息论方法也常用于构建此类波段选择方法，如基于互信息的方法MI （Mutual Information）、基于特征分析的方法（MVPCA、MSNRPCA）（Chang 和Du，1999；Chang，1999；Chang 等，2021）等。该类方法不需要对数据分布与类别密度函数进行任何假设。

第二类为非监督滤波型波段选择方法。该类方法不需要考虑特定应用，直接利用数据相关性进行波段选择或利用信噪比（SNR）删除噪声较大的波段（Patro 等，2021；Roy 等，2021）。其缺点是信息冗余去除效果不佳，因此可选择相互之间最不相似的波段，如线性预测方法LP （Linear Prediction）（Du 和Yang，2008），或聚类子空间方法（Cluster space）等都可以实现降低波段间冗余度的目的。

2.2.2 搜索优化策略

由于高光谱遥感影像数据的信息量非常大，导致特征选择的搜索空间较大，因而大部分特征选择算法的空间复杂度比较高，应用时存在较大难度；因此，解决了特征选择算法的信息测度函数之后，改进其搜索方式成为亟需解决的问题，也是当前的研究热点。根据不同情形，可采用以下搜索策略。

（1）穷尽搜索（Exhaustive search）。该方法在搜索空间内遍历所有可能的波段组合（Coban 和Mersereau，1998），其特点是一般能搜索到最优解，但是随着高光谱遥感数据特征维数的增加，算法复杂度会急剧增长；该方法只在特征数目较少时才比较合适，对于高光谱遥感数据，可采用贪心搜索方案。

（2）贪心搜索（Greedy search）。该方法利用数学模型将拟求解问题分解成多个子问题，并将子问题的局部最优解合并成拟求解问题的最终解。常用算法有分支界定法B&B（Branch and Bound）（Somol 等，2004）、序列前向选择SFS（Sequential Forward Selection）（Serpico 和Moser，2007）和序列后向选择SBS （Sequential Backward Selection）（Sun 等，2014）等。以上方法中，序列前向选择和序列后向选择算法缺乏反馈机制，限制了被选波段或被删除波段的后续效应。可以在SFS 和SBS算法中加入浮动搜索策略，得到搜索效率更为高效的序列浮动前向选择SFFS（Sequential Floating Forward Selection） 和序列浮动后向选择SFBS（Sequential Floating Backward Selection）等方法（Su等，2014）。该类算法选择的特征子集在局部是最优的，但却不是全局最优的。

（3）启发式搜索（Heuristic search）。该方法利用拟求解问题拥有的启发式信息构建相关函数，进而提升搜索效率。群体智能优化即属于启发式算法，如遗传算法GA（Genetic Algorithm）（Yao 和Tian，2003）、克隆算法CSA （Clonal Selection Algorithm）（Zhang 等，2007）、粒子群优化PSO（Particle Swarm Optimization）（Yang 等， 2012；Su等，2014）和萤火虫算法FA（Firefly Algorithm）（Su 等，2016）等已经被用于高光谱遥感波段选择，并取得了较好的效果。由于启发式搜索只有有限的信息，其难点在于需要在局部搜索与全局搜索之间取得平衡，避免陷入局部最优解。

2.2.3 最优波段数目

波段选择时若干含有丰富信息的波段被保留下来，至于保留多少数目的波段，并没有固定的数字，一般取决于数据本身的特点，这一直以来都是波段选择算法面临的重要问题，也是高光谱遥感影像降维的难点问题。目前有3种解决方案。

（1） 虚拟维度VD （Virtual Dimensionality）。VD 是指高光谱遥感数据中不同地物类别的光谱曲线个数（Chang，2018），可用于衡量波段数目的指标（Chang 和Du，2004；Chang，2009）。如提出的信道容量（Channel capacity）思想，即利用SQ-CCBSS 和SC-CCBSS 算法进行波段选择，同时可以进行最优波段的判定（Chang 等，2017）；该方法首先利用VD 判定波段子集大小，然后利用波段判别指标构建全波段与已选波段子集之间的波段信道传播概率矩阵，基于Blahut算法求解波段的信道容量，利用SQ-CCBSS 和SC-CCBSS 算法寻找最优波段子集。

需要注意的是，在高光谱遥感影像降维中，会涉及到本征维数ID（Intrinsic Dimension）的概念（Camastra 和Staiano，2016），ID 指的是重构高光谱遥感数据所必需的自由变量的最小数目；它与VD 是不同的，总体上说，ID 完全取决于需要处理的数据，而与应用无关。因此，ID 经常表述为一个单一的固定常量，不随应用的变化而变化。另外，需要特别注意的是，降维后需要保持的数据维数，与波段选择所选择的波段数并不是相同的；因此，单一的ID 值无法用于这种一对多应用。与ID 相对应，VD 则是指高光谱遥感数据中不同地物类别的光谱曲线个数，可表述为Neyman-Pearson探测问题，因而VD 的值可以随虚警率而变化，可根据不同的应用进行调整。从理论上讲，VD 比ID更适合和高效地应用于需要提供感兴趣目标的高光谱遥感数据探测应用（Chang，2018）。但是该算法也存在问题，因此，需要寻找一种简单、高效的特征数目自动判别方法。

（2）端元提取（Endmember）。如果假定选择某个合适的波段类似于寻找某个端元，那么最优波段子集实际上与在所有可能的端元之中选择的最优端元子集类似，即找到了p个最优端元也就类似于找到了p个最优波段。常见的端元提取方法如，N-FINDR、IEA、VCA、ICE、AMEE 等都可以用于最优波段子集确定（Plaza 等，2004；Zare和Gader，2008；Chang 和Liu，2014；Song 等，2021）。在最优端元子集确定时，该类方法一般采用穷尽搜索方式，可能会付出较大的时间代价，而后续提出的序列N-FINDR 算法等则可以解决此问题（Wu等，2008）。

（3）群体智能优化。如果拟选择的波段数目已知，可直接利用上述单一群体智能算法进行波段选择。然而，如果拟选择的波段数目发生变化，则需要重新运行该算法。不幸的是，对于某一高光谱遥感数据来说，很难事先估计最佳的波段选择数目。因此，可以构建多目标群体智能优化算法（Gong 等，2016），如近年来提出的基于组合型PSO 的自适应波段选择系统（2PSO）（Su 等，2014），该系统耦合了两个不同的PSO 优化过程，其中内部PSO 作为外部PSO 的其中一个粒子，负责搜索已定数目的具体波段；该算法可同时确定最优波段数目并进行具体波段选择。另外，还有MOPSO （Paoli 等， 2009）、 MOBS （Gong 等，2016）、APBI（Pan 等，2019）和稀疏自表达多目标优化（Hu等，2019）等算法。

2.2.4 多特征质量评估

特征提取和波段选择可得到高光谱遥感影像的多种特征，如光谱特征、空间特征、纹理特征、上下文特征等；面对丰富的特征信息，哪些特征对后续应用更有效成为亟需考虑的问题。目前基本是使用所有特征或单一特征或某几个特征进行后续分析，没有考虑特征与地物类别之间的相关性；特征选择的主观性、冗余性导致后续分析的可靠性、稳定性无法保证。因此面对后续应用需求和特点，有必要对提取的多种特征进行质量评估。目前的评估方法可以归纳为定性和定量等两类。

（1）定性评价。1）散点图。又称为散点分布图，是利用散点（样本点）在不同特征空间下的分布形态反映特征之间统计关系的方法（Tyo 等，2003）。二维散点图就是在二维特征空间中，选取几种典型地物类别，将属于不同类别的已标记样本点绘制在二维特征空间中，根据不同类别的散点图之间的聚集与分散程度可以直观地表达特征空间的可分性（图7）。然而二维散点图仅能表达样本点在两个特征空间之间的统计关系，不能反映多个特征空间之间的可分性，高维特征空间的散点图难以绘制，该方法只能作为数据的初步分析工具。

图7 DC数据典型地物样本的散点图Fig.7 Scatter plot of typical feature samples in DC data

2）概率密度函数图。给定一维特征空间，在95%置信度条件下估计典型地物类别在该特征空间下的均值和方差，利用估计值计算典型地物类别的概率密度函数（Matteoli等，2014）。该方法的特点是可对较难区分的地物类别给出直观评价，其思路是将不同地物类别的正态分布相叠加，正态分布特征的重叠情况即反映不同地物类别在给定特征空间的分离程度（图8）。

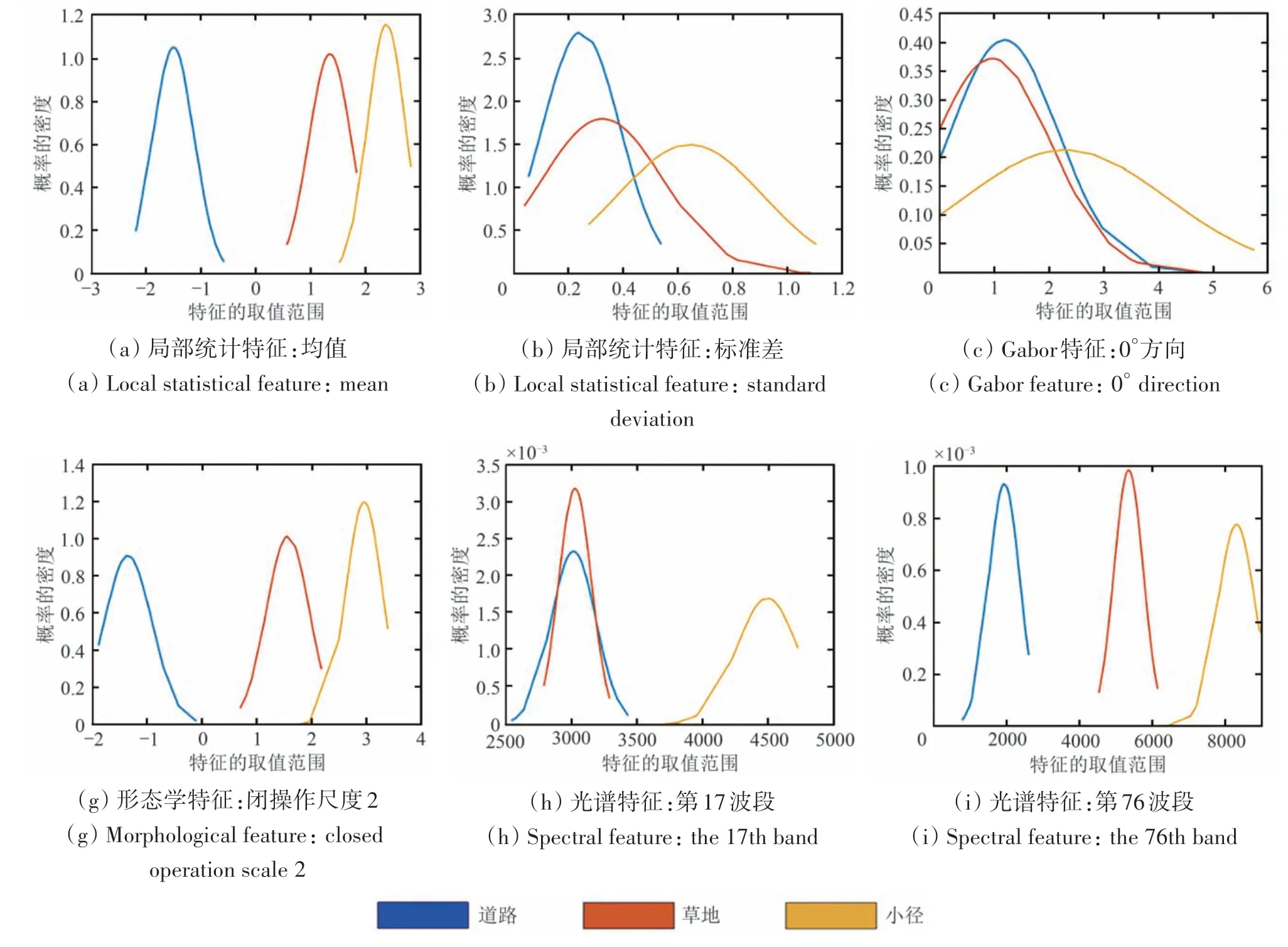
图8 DC数据典型地类概率密度函数图Fig.8 Typical probability density function graph of DC data

3）相关系数矩阵图。相关系数可以衡量变量之间相关性（Su 等，2011），其值在0 到1 范围，呈正相关；其值在-1 到0 范围，呈负相关。计算每两个特征间的相关系数，将求得的相关系数矩阵绘制成图，即是特征的相关系数矩阵图（图9）。相关性矩阵是对称矩阵，其对角线上的元素值均为1，为每个特征的自相关系数。

图9 DC数据相关矩阵图Fig.9 DC data correlation matrix

（2）定量评价。1）信息度量。即量化随机变量之间的不确定性，且不局限于线性关系，其主要指标包括信息熵、信息增益、互信息等，其中信息熵是衡量影像信息含量的重要方法（Song 等，2019），能够利用图像中的变量分布情况描述变量的分散程度，可用于表征遥感影像的信息测度。每个特征的信息熵值反映了特征信息的含量，信息熵越大，影像数据的离散程度越大，信息量越丰富，即在图像中描述这个变量所需的信息也越多。图10给出了DC数据各波段的信息熵。

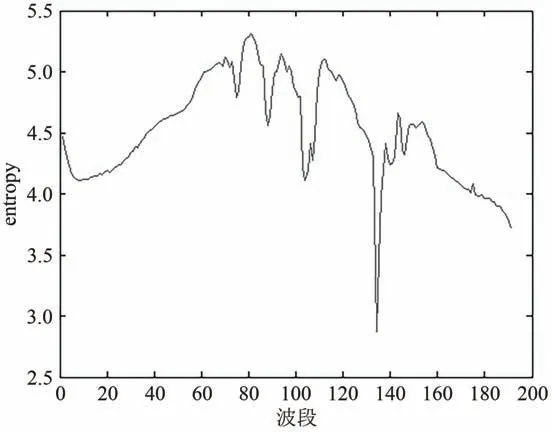
图10 DC影像不同波段的信息熵Fig.10 Information entropy of different bands

2）直方图。反映了影像亮度值出现频率的信息（Ni 和Ma，2015），并可展示图像的灰度最小最大值、众数等特征，直方图中的峰对应着主要的地面覆盖类型，亮度值出现频率的分布范围对应着相应的对比度。图11 给出了DC 数据在第10和60 波段的直方图，可知，第10 波段的亮度值被压缩到0—255区间低值的1/3值域内，说明影像对比度相对比较低；而第60 波段则分布较广，对比度相对较高。从峰值上来看，第10 波段的直方图只有3个峰值，而第60波段则有6个峰值（反映了6类地物：道路、草坪、水体、小径、树林和建筑物），这也印证了影像对比度的结果，因为只有在对比度较高的图像上才能分辨出更多的地物类型。

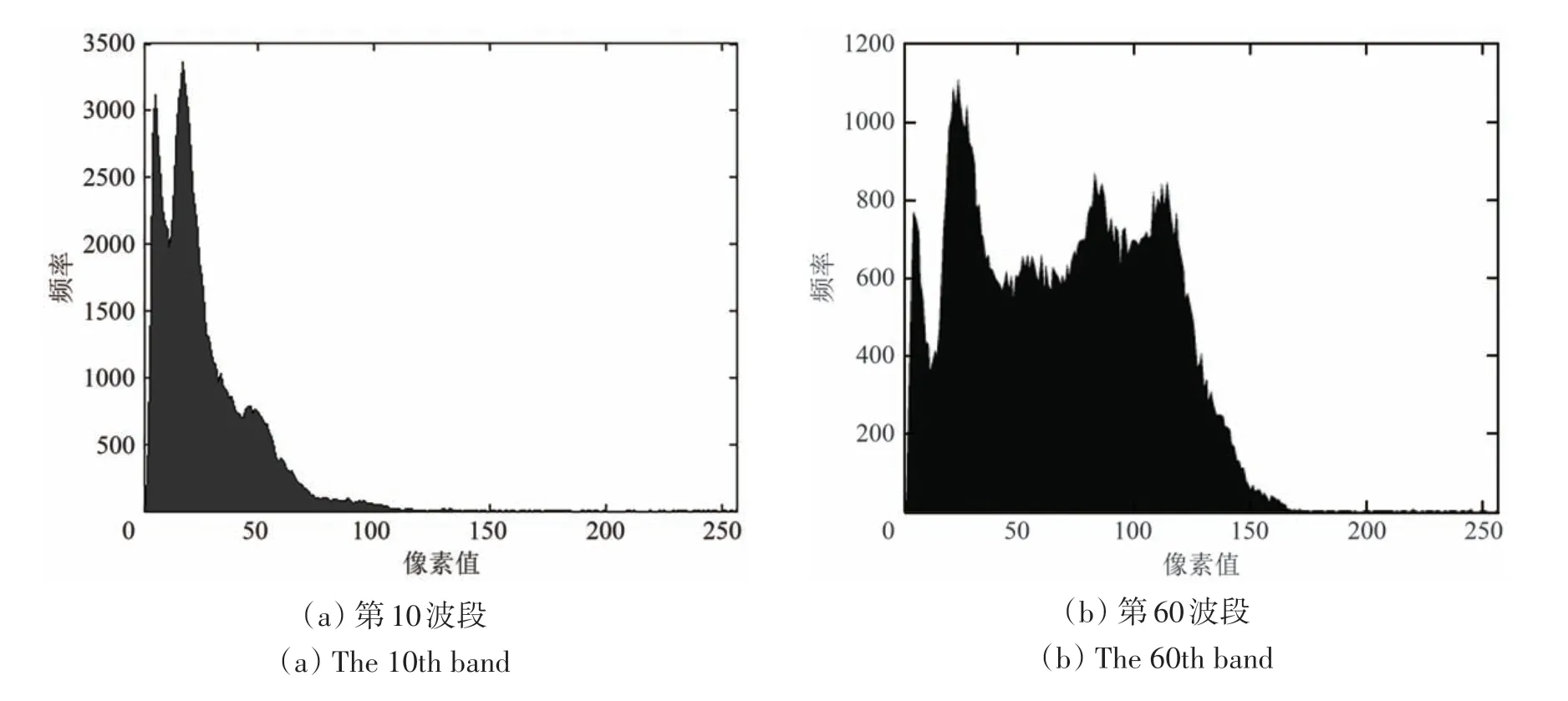
图11 DC 影像第10和60波段图像的直方图Fig.11 Histograms of 10th band and 60th band of DC image

3）信噪比。高光谱遥感数据在获取过程中由于受到内外因素的干扰，会产生很多意想不到的噪声，且具有以下特性：特征1：基本上属于高斯白噪声，多数情况下，噪声与信号、噪声与噪声之间不具备相关性；特征2：像素之间的噪声具有相关性，但是在不同波长处的变化较为复杂；特征3：具有空谱维的独特特性。高光谱遥感影像在地物类型均一的情况下，数据服从正态分布，虽然噪声较小，但严重影响数据质量和地物的光谱辐射特性，因此，噪声消除是高光谱影像处理中不可缺少的环节。一般可用图像的信噪比来衡量数据中噪声所占比例，计算信噪比时需要选择地物类型均一的局部数据，特别是选择受环境因素影响较小的区域（Conoscenti 等，2016）。图12 为DC高光谱遥感数据各波段的信噪比。

图12 DC影像各波段SNRFig.12 SNR of each band for DC image

由信噪比的定义可知，信噪比大的波段其图像质量要好于信噪比小的波段；若与各波段的信息熵（图10）相比较，可发现信息熵大的波段其信噪比也较高。另外，与系统误差造成的噪声相比，图像背景对图像质量干扰的影响也较大，光谱混合现象是造成图像波谱变化的主要因素。因此，利用光谱解混技术对高光谱遥感影像进行处理至关重要。

4）特征与类别间的相关性。互信息是衡量特征与类别之间相关性的重要指标，对于两个随机变量，它们在某种程度上存在着一定的统计依赖关系，互信息则反映了这种关系（Feng 等，2015）。如果一个特征与某一地物类别相关，则其互信息值较高。

5） 类别可分性评价。费舍尔比率（Fisher Ratio）利用类内与类间散布矩阵的比值构建判别函数（Du，2007），可以用于评价特征的类别可分性。

2.2.5 多特征优化

当前的高光谱遥感应用对特征信息的利用基本是将光谱特征和某些空间特征进行融合（Bioucas-Dias 等，2013；Fauvel 等，2013），且对同一影像中不同的地物类别使用完全一致的特征集，没有考虑特征与地物类别的相关性；因此，需要根据数据的具体特点对高光谱遥感的多种特征（光谱、纹理、上下文）进行选择和优化。目前国内外对该方面进行了初步研究，如提出了能同时选择波段并确定波段数目的多目标优化波段选择方法（Multiobjective optimization band selection）（Gong 等，2016）、能充分利用特征信息的多特征学习方法（Multiple feature learning）（Li 等，2015a）、一种基于流形学习和块对齐的多特征结合方法（Multiple feature combining）（Zhang 等，2012）、一种能同时进行空谱特征选择和提取的方法（Zhang 等，2018a）等。目前的研究主要针对不同的应用目的分别展开，无法形成针对高光谱遥感影像多特征优化的方法框架。

构建高光谱遥感的多特征优化模型是当前高光谱遥感领域的研究热点和研究难点。多特征优化模型的构建需要解决两方面的问题：一是采用何种指标作为目标函数来评价不同特征的质量，该评价指标可根据具体应用目标构建或借鉴波段选择算法中的信息测度实现（Chang，2000；Yang等，2011）；二是使用何种搜索策略实现优化，现有的搜索算法有3种：即穷尽搜索、贪心搜索和启发式搜索等。其中，穷尽搜索虽能够得到最佳结果，但针对高光谱遥感时搜索空间过大、空间复杂度过高，因此该方法不太可取；次优的搜索方案即贪心搜索，如分支界定法（B&B）、序列前向选择（SFS）、后向删除法（SBS）等，但是该类方法缺乏反馈机制；具有反馈机制的SFFS和SFBS方法可进一步提高搜索的效率。近年来，新型启发式搜索方法如群体智能优化在高光谱遥感领域得到了快速发展，如克隆算法、粒子群优化、萤火虫优化等（Xue 等，2013），特别是萤火虫算法具有的操作简单、高效计算、参数少等优点，为多特征优化模型的搜索策略设计提供了新途径（Su等，2016）。

综上，需要强调的是，波段选择和特征提取并不是截然分开的，如可以先将原始特征空间映射到维数较低的空间，然后再进行特征选择；也可以先去除明显没有信息的特征，再进行映射以降低维数。二者并没有逻辑的先后关系，使用哪一种方法取决于应用场景和目的。

3 高光谱遥感影像降维的挑战

总体来看，当前对降维技术的研究主要集中在特征提取和波段选择等方面，特征提取研究主要侧重于统计理论、空间域、流形学习和深度学习等角度；波段选择研究则侧重于信息测度、搜索策略和评价标准等方面。高光谱遥感影像降维技术的实质在于构建合适的函数对数据进行有效处理，但是都存在一定问题：特征提取方法主要用变换函数获取降维后的少数特征，算法复杂度高，且降维后的特征丢失了物理意义；而波段选择则利用信息测度从原始数据中优选出波段子集，不可避免地丢失了部分信息；同时，多种特征下如何进行优化以及合理的降维特征数目仍是当前高光谱遥感影像降维研究中的难点问题。因此，高光谱遥感影像降维技术面临着诸多挑战，下面主要从特征可分性、特征质量评价、特征数目确定、多特征优化和需求驱动的特征选择等方面，对高光谱遥感影像降维技术面临的挑战进行分析。

3.1 特征可分性

特征提取往往面临特征可分性度量问题，特征可分性即评价特征对地物分类有效性的定量指标。高光谱遥感影像的信息分布特征与多光谱遥感影像明显不同，设计特征可分性指标时需考虑其独特的信息空间分布特征。一般的多光谱遥感数据使用均值即可得到较好的分类结果；然而，高光谱遥感数据的不同地物类别的均值可能很近，且其数据分布可能比多光谱更为复杂，此时使用标准差或同时使用均值和方差进行分类会得到比单纯使用均值更好的分类结果（Chang，2013）。以上情况说明，针对多光谱遥感数据，数据分布的位置比形状和方向重要；而针对高光谱遥感影像，其数据分布的形状和方向却比位置重要。因此，对高光谱遥感数据进行特征可分性研究时，不仅仅要关注其数据分布位置，而且要特别考虑数据的空间分布形状和方向，进而才能设计出符合其数据特点的可分性度量指标。

3.2 特征质量评价

特征是高光谱遥感影像数据的重要信息，无论是在特征选择还是特征提取中，对特征质量进行评价都十分必要，但是目前这方面的研究却比较少。一般来讲，特征提取的质量评价方法可分为3 类（Lee 和Verleysen，2009；薛朝辉，2015）：（1）依据数据重建误差进行评价，然而大多数非线性特征提取方法并不能给出特征映射函数的闭式形式；（2）以任务为驱动的评价标准，根据应用需求的先验知识，可采用分类精度、目标探测准确率等对特征质量进行评价；（3）根据对数据结构的保持能力进行评价，从本质上讲，特征提取方法目标函数的构建往往要求其对数据结构的保持能力较好，具有较好数据结构保持能力的方法提取的特征的质量自然也较好。

总体来看，目前的研究主要利用定性方法（散点图、概率密度函数图、相关系数矩阵图）和定量方法（距离测度、直方图、信噪比、特征与类别间的相关性评价、特征的类别可分性评价）等对特征质量进行评价。其中距离测度是当前研究的热点方向，其实质是衡量特征或样本之间相似程度的指标，测度学习的目标是使同类样本间的距离尽可能小，而不同类样本间的距离尽可能大，这是模式识别研究的核心问题。基于样本的标签信息和特征的统计信息，距离测度函数可对不同遥感影像的相似性或特征的有效性进行判断（Dong 等，2017）；例如马氏距离测度，即是通过寻找描述不同样本之间的马氏距离，进而建立不同特征向量之间的关系，并有效保留样本的相似关系。

对于目前的高光谱遥感降维算法来讲，大多数算法均假定影像的信息服从高斯分布，且存在参数敏感、鲁棒性差等问题。然而，在真实的高光谱遥感影像中，地物种类实际上繁多且分布非常复杂，从而导致在现有测度空间内很难有效描述样本或特征分布，也很难构建可靠的距离测度函数。另外，从样本空间的角度来看，现有方法大多对不同样本的相似性进行简单度量，没有详细考虑同类地物之间的相似性以及不同类地物之间的差异性的特性，导致无法精细刻画样本或特征之间的区别和联系，使得降维效果欠佳。最后，比特征质量评价更为困难的是，如何对特征提取方法本身的性能进行评价，这也是特征提取面临的另一个重要难点问题。

3.3 特征数目确定

高光谱遥感数据降维不可避免地会涉及到降维后特征数目的问题，目前的方法大部分都是人为设置降维后的特征数目，无法与后续应用需求相关联。如PCA 方法降维时，将原始数据投影到由几个向量构成的特征空间并使投影误差最小，一般选择能使误差小于0.01（保留99%的信息）的维数。另外，也可根据特征值累计值曲线拐点对应的维数进行判断。以上思路可用于非监督降维的特征数目确定问题，但是该类算法无法与后续应用建立关联，使得其应用前景大打折扣。

而对于监督式降维算法特征数目的问题，必然需要考虑降维后特征数目与样本之间的复杂关系，这一直是高光谱遥感影像降维研究中的难题（Chang，2013）。常采用的虚拟维度方法，实际上是分析影像中地物类型的个数，以地物类型个数作为降维后的特征数目。端元提取方法则利用从影像中提取的最优端元子集个数判定降维后的特征数目，从本质上讲，该方法是VD 方法的扩展，当最优端元子集个数等于地物类型个数时，该方法即为VD 方法；但当最优端元子集个数大于地物类型个数时，则是一种新情况；该方法的问题是随着端元的变化最终结果存在较大变数。而最近提出的基于群体智能算法的特征数目自适应判别方法，由于存在两个群体智能算法的嵌套，算法复杂度较高，应用推广比较困难。

根据高维空间的参数估计理论，在分类精度一定的情况下，空间维数越高，所需的样本数目越多。因此，从样本数据与降维特征的关系出发，降维后的特征一般要小于样本数，才能使后续应用得到较好的效果，这也是未来算法设计时可参考的思路。

3.4 多特征优化

多特征优化实际上包含两方面的内容，一是在众多特征中，哪些特征对后续分析有效，即涉及到特征质量评价问题；二是面对多种特征，如何进行优化，即涉及多特征优化模型问题。多特征质量评价方面，现有研究大多集中在高光谱遥感影像的特征提取或少数特征的应用方面，面对丰富的特征信息，针对特征与类别的相关性对特征进行评价的研究较少，目前的难点在于针对高光谱遥感特征质量评价还没有统一的标准方法。

多特征优化模型方面，一方面需要利用多特征质量评价的方法作为优化模型的目标函数，另一方面，需要根据高光谱遥感影像数据的特点，选择合适的搜索策略构建多特征优化模型，搜索策略的确定也是研究中的难点。当波段数目不多时，如多光谱遥感数据，穷尽搜索法是可行的，即通过穷尽搜索，评价各个可能的特征子集的性能，进而找到最优子集；该方法比较直接，不会漏掉任何一种可能的子集，但是由于要穷尽所有可能，导致运算量巨大，特别是面对上百波段的高光谱遥感数据时，效率过于低下。与穷尽搜索不同，贪心算法在处理数据时，往往是从局部空间得到其局部最优解，该算法的缺点是不能保证结果最佳。启发式搜索则在一定搜索空间搜寻到最好的解，如近年来兴起的群体智能算法等。现有研究表明，动物在进行决策时采用的即是启发式策略，其搜索策略一般遵循莱维飞行原理，具有随机、方向不定、步长不定等特点，因此，能够更有效、快速地找到局部最优解。启发式算法的特点是找到的解虽在一定程度上是满意的，但却不一定全局最优；其关键是如何建立满足应用需求的启发式规则，其难点是在局部与全局搜索之间取得平衡并能迅速跳出局部最优解，这也是未来研究的热点问题。

近年来，作者在高光谱遥感影像多种特征提取的基础上，改进最新的群体智能优化（如萤火虫算法、布谷鸟搜索等）算法，设计有效的目标函数对多特征质量进行评估，基于设计的搜索策略对多特征进行优选，进而构建了高光谱遥感影像的多特征优化模型（Su 等，2014，2016；刘慧珺等，2018），为相关研究做出了初步探索。高光谱遥感多特征优化模型将是未来高光谱遥感研究中的热点问题。

3.5 需求驱动的特征选择

目前的高光谱遥感影像降维主要针对高光谱遥感原始数据的特点进行，属于数据驱动的降维；少部分则针对后续的高光谱遥感应用选取合适的特征，属于需求驱动的降维。随着高光谱遥感数据获取技术的进步，其应用领域也越来越广泛，应用需求驱动的特征选择主要包括：（1）地物分类驱动的特征选择，所选出的特征应能突出不同地物类型的可分性（Alsuwaidi 等，2018；Fassnacht等，2014）；（2）目标探测驱动的特征选择，所选出的特征应能够有效地将背景与目标进行区分，同时突出异常目标（Xie 等，2020）；（3）混合像元分解驱动的特征选择，所选出的特征应能够充分反映纯净像元（即端元）的光谱特征，同时使不同端元之间的区分度更强（Chang 和Liu，2014）；（4）跨场景的特征选择，该类方法不仅需要考虑每一场景中不同地物类别的可分性，还要顾及不同场景下特征的一致性（Wang 等，2021）。需求驱动的特征选择的关键问题是首先要明确遥感应用拟解决的科学问题是什么，进而根据科学问题选择出合适的特征，从而提高特征选择的针对性，这也是需求驱动的特征选择的难点问题和未来的研究热点。

4 结 语

高光谱遥感作为对地观测领域最具活力的重要技术突破，是21 世纪遥感领域最为重要的研究方向之一。随着高光谱遥感技术的快速发展，面对高光谱遥感数据急剧增加的挑战和信息高效处理的要求，如何从海量高光谱遥感数据中快速有效地提取知识已成为限制高光谱遥感应用的瓶颈问题，也是当前亟待解决的问题。综合以上相关研究的进展以及存在的挑战，可以看出，高光谱遥感影像降维研究主要有以下发展趋势：

（1）高光谱遥感智能降维技术成为未来的发展方向。随着智能化高光谱遥感对地观测系统（张兵，2011a）的提出，高光谱遥感的智能化信息处理可以利用机器学习方法，结合相关应用需求，从海量的高光谱遥感数据中挖掘出感兴趣的信息，这是未来的重要发展方向。因此，需要利用多学科交叉的知识，充分发挥机器学习、模式识别、人工智能、大数据科学等新理论、新方法的优势，建立高光谱遥感的自适应性降维新方法，进一步提升高光谱遥感信息处理的质量和效率，充分发挥高光谱遥感大数据的优势。

（2）高光谱遥感多目标降维技术是未来的研究热点。高光谱遥感降维技术的关键在于特征质量评估、搜索策略优化、满足应用需求等，其难点在于如何构建相应的函数。目前的研究基本集中在某一单一目标，如为提升特征质量评估效果而设计的新型目标函数指标；为提升降维效率而设计的新型群体智能搜索算法；为与后续应用对接而设计的监督降维方法等。采用多种目标同时优化的研究虽有一些初步探索，但还远远满足不了地学应用的需求。

（3）需求驱动的高光谱遥感影像多特征智能优化将成为新兴方向之一。目前的大多数降维方法实际上是对原始高光谱遥感数据直接进行特征选择和特征提取，进而得到某些有用特征；实际上，根据应用需求对特征进行针对性选择，应更为有效。另外，经过多年发展，已经涌现了大量高光谱遥感特征提取方法，提取出的特征也非常多，如选择的波段、聚类特征、纹理特征、形态学特征、空间特征、上下文特征等，形成了多种特征并存的现象。因此，针对高光谱遥感影像丰富的多特征信息，结合应用目标需求，考虑特征与类别的相关性，设计高光谱遥感影像多特征智能优化模型将成为新的研究热点。

总之，高光谱遥感影像降维技术在国内外取得了较为显著的成绩，已成为高光谱遥感影像研究领域的热点和重要方向之一。目前世界各国已有大量在轨和拟发射的高光谱遥感传感器，高光谱遥感的数据获取能力空前提升，进而也会推动高光谱遥感的深入应用。因此，从数据处理和应用需求等方面都对高光谱遥感影像降维技术提出了更高更广的要求，高光谱遥感影像降维将迎来更为严峻的挑战，也为其发展带来了机遇。高光谱遥感影像降维技术的发展，一方面将会进一步推动高光谱遥感数据处理理论和方法的发展，另一方面也会进一步推进高光谱遥感数据的广泛深入应用，具有较高的科学意义和应用前景。