风电场黑启动储能容量优化配置：一种考虑储能运行策略的方法

闫来清，曹丽源，薛太林，张学军，王 祺

风电场黑启动储能容量优化配置：一种考虑储能运行策略的方法

闫来清，曹丽源，薛太林，张学军，王 祺

(山西大学电力与建筑学院，山西 太原 030006)

风电在区域电网的占比越来越大。为了解决风电场在黑启动过程中的风电出力波动问题，提出了一种考虑储能运行策略的储能配置方法。首先，基于风电功率预测算法得出预测功率，并利用非参数核密度估计定义黑启动最小风功率概率密度以及黑启动可执行概率倾度，进而确定了黑启动时段。其次，根据储能在黑启动过程中补偿功率缺额和平抑波动作用制定储能运行策略。考虑储能运行策略对容量配置的影响，将储能额定功率和额定容量作为模型自变量，建立以补偿功率缺额最大化为目标函数的储能优化配置模型，并采用改进粒子群算法对模型进行求解。最后，以内蒙古某45 MW风电场数据对储能运行策略和优化配置模型的可行性进行了验证。

黑启动；非参数核密度估计；概率密度；储能运行策略；储能容量配置

0 引言

近几年国外先后发生了许多次大停电事故，这无疑给电力系统敲响了警钟。例如，土耳其“3·31”大停电事故造成40多万家企业和家庭停电，美国加州2020年轮流停电事故[1-2]。由于现代社会对电力供应的依存度越来越高，大停电事故造成的后果日趋严重[3-4]。随着我国碳达峰目标的提出，可再生能源发电的比例将越来越大，风力发电、光伏发电等作为黑启动电源将是未来的发展趋势[5-7]。但是，风力发电、光伏发电具有波动性、间歇性的特征，随着储能大规模利用，使得风光发电的功率波动得到巨大改善[8-11]。风储系统作为黑启动电源的可行性已得到论证，储能结合风力发电可以作为黑启动电源[12]。

风储系统作为黑启动电源，储能的主要作用是平抑风电功率波动和补偿功率缺额。文献[13]将风电时间序列分解为自适应优化的小波参数，结合鲁棒模型预测控制策略(Model Predictive Control, MPC)，以电池输出和超级电容器的方差最小为目标函数，限制功率波动。文献[14]以日运行成本最小为目标，综合考虑火电、抽水蓄能和电池储能建立二阶锥储能规划模型。文献[15]根据电池退化模型，考虑储能容量保持率对储能配置的影响，以实现储能的经济配置。文献[16]提出了基于改进粒子群优化的混合储能系统功率波动控制策略，将滤波器作为功率分配控制策略，结合控制要求提出多目标函数，用粒子群算法求解目标函数得到了电池和超级电容的具体容量参数。文献[17]采用一阶低通滤波将超导磁储能和蓄电池分成高低频，进行功率分配，在综合考虑投资成本和维护成本的基础上，建立了超导磁储能和混合储能系统年成本最小的目标函数，求取储能容量配置。但功率分配没有考虑储能荷电状态(State of Charge, SOC)。文献[18]为了平滑风电波动，提出了一种基于频率的混合储能系统规模确定方法。文献[19]以综合净收益最大化为目标，建立双层优化决策模型，实现黑启动以最佳顺序恢复。文献[20]以需要平抑的最大功率波动为约束目标，实现风电场初期黑启动储能优化配置。文献[21]同时考虑风电出力波动约束和储能自身约束，提出了将风电和储能作为黑启动电源的储能配置策略。文献[22]利用Copula函数分析储能容量和功率的相关性，提出以储能配置成本最小为目标的储能配置方法。文献[23]采用线性加权法构建储能初始SOC和容量的双目标模型，以实现经济性最优。文献[24]考虑风电场选址和被启动机组的启动顺序建立分层规划模型，并考虑母线电压平衡，实现储能的最优配置。

由以上文献可知，针对风电出力波动，主要采用混合储能，以风电波动最小或储能成本最小为目标建立优化模型，再利用优化算法进行求解。针对黑启动的储能配置文献较少，主要是通过考虑风电厂位置、被启动机组启动顺序或最大缺额功率进行容量配置，没有考虑储能运行策略对储能配置的影响。本文通过风电预测算法确定未来1 h的风电出力，采用非参数核密度估计，定义风电场黑启动的可行性评估指标，确定风电启动时段，并结合黑启动过程的功率缺额和功率溢出状态下的储能运行策略，以补偿功率缺额最大为目标函数，建立优化模型，并采用改进粒子群算法求解模型。最后利用内蒙古某风电场数据验证所提方法的有效性。

1 影响因素分析

风储系统作为黑启动电源结构图如图1所示，风电场在储能系统的辅助下，在得到黑启动的指令后，储能配合风电场自启动，向空载线路供电，启动火电场辅机，最终联合火电机组恢复局部电网的供电。

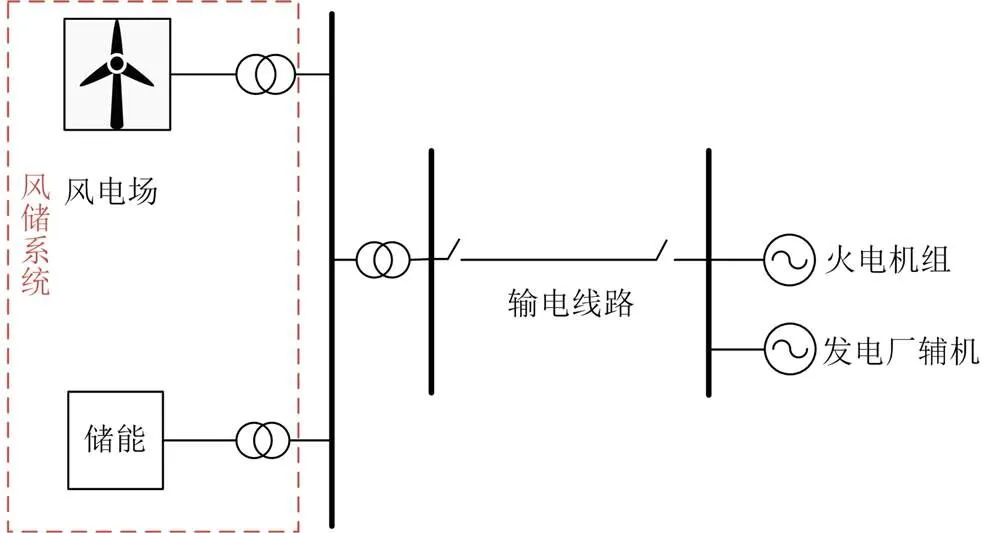
图1 风储系统作为黑启动电源结构图

风储联合系统在火电机组黑启动过程中，由于风电出力的波动性，储能系统主要的作用是稳定频率、完成风机自启动和补偿功率缺额。结合储能自身特性，在黑启动过程中储能配置需考虑如下的因素。

1) 风电场在不同时间风速等周围环境变化下出力水平相差甚远，需要对未来一段时间的风电出力进行预测。由于风电场并不是每个时段都可以执行黑启动，需要根据预测出力确定满足黑启动的时段，保证黑启动能够执行，减少功率缺额，实现间接减少储能成本的目的。

2) 黑启动过程中，当风电出力小于辅机功率时，需要储能补偿缺额；当风电出力大于辅机功率时，如果储能将溢出功率全部吸收，储能容量太大导致成本太高。应当考虑制定合理的储能运行策略，保证黑启动运行的同时可以将多余功率向其他负载供电，实现减少弃风和提高新能源利用率的目的。当然，储能必须在指定SOC工作区内，不然会影响储能的寿命。

3) 由于风机自身没有自启动能力，也需配置一定储能来完成自启动，但由于平滑黑启动所需功率远大于自启动所需的能量，所以只考虑黑启动过程中功率缺额部分。

根据以上分析，确定风储联合系统作为黑启动电源的储能容量优化配置策略如下：基于风电预测算法对未来一段时间的风电出力进行预测，利用非参数核密度估计分析未来一段时间风电出力的概率密度，进而确定黑启动可执行倾度，确定可执行的时间段。根据储能运行策略，确定以最大化补偿黑启动缺额功率为目标函数的优化模型，由此得出储能额定功率及容量，确保风储系统完成整个黑启动过程。

2 储能配置方法

2.1 风电场黑启动可执行时段确定

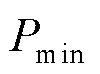
黑启动要求最小出力约束为

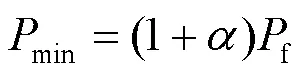
由于风电出力的波动性，而黑启动需要至少1 h的连续供电，这其中包括了风电场自启动、输电线路充电、辅机启动等一系列过程。因此，黑启动运行时段，风电场必须能够持续供电。为了准确描述风电功率的变化，确定当前时段的黑启动可行性，以保证整个黑启动正常运行，基于非参数核密度估计的风功率概率密度函数为

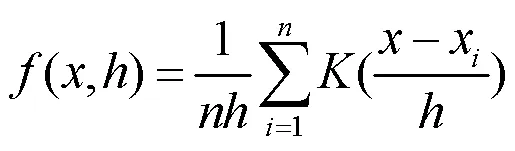
由于核函数有许多的选择，根据文献[25]，为了保证概率密度函数的连续性，本文选用高斯函数作为核函数，可表示为

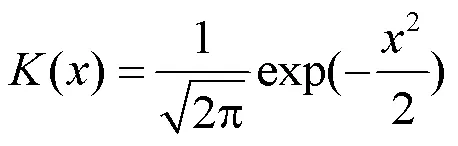
则最终的风功率概率密度函数为

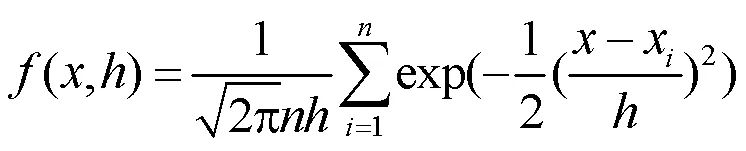
由于风储系统要实现黑启动，需满足黑启动的最小出力条件，当风电场出力小于辅机需求功率时，需要储能补偿；当风电场出力大于辅机需求功率时，由于储能现阶段成本高昂，常常采用限制出力水平与弃风操作。考虑到黑启动过程中，风电场出力必须有一段时间的持续性，因此，以黑启动最小出力为条件概率密度的下限，定义黑启动最小风功率概率密度为

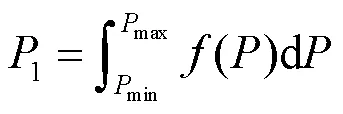
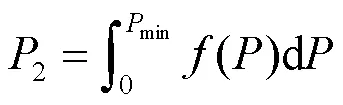
则黑启动可执行的概率倾度为

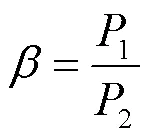
2.2 储能运行策略

为了使黑启动正常进行，不仅要考虑储能的充放电效率、SOC、当前可充放电功率等，保证各项指标达到黑启动标准，还应考虑储能运行策略的影响。储能的运行策略直接影响储能能否正常工作，本文储能运行策略如图2所示，补偿缺额和平衡波动的时间尺度为1 min。

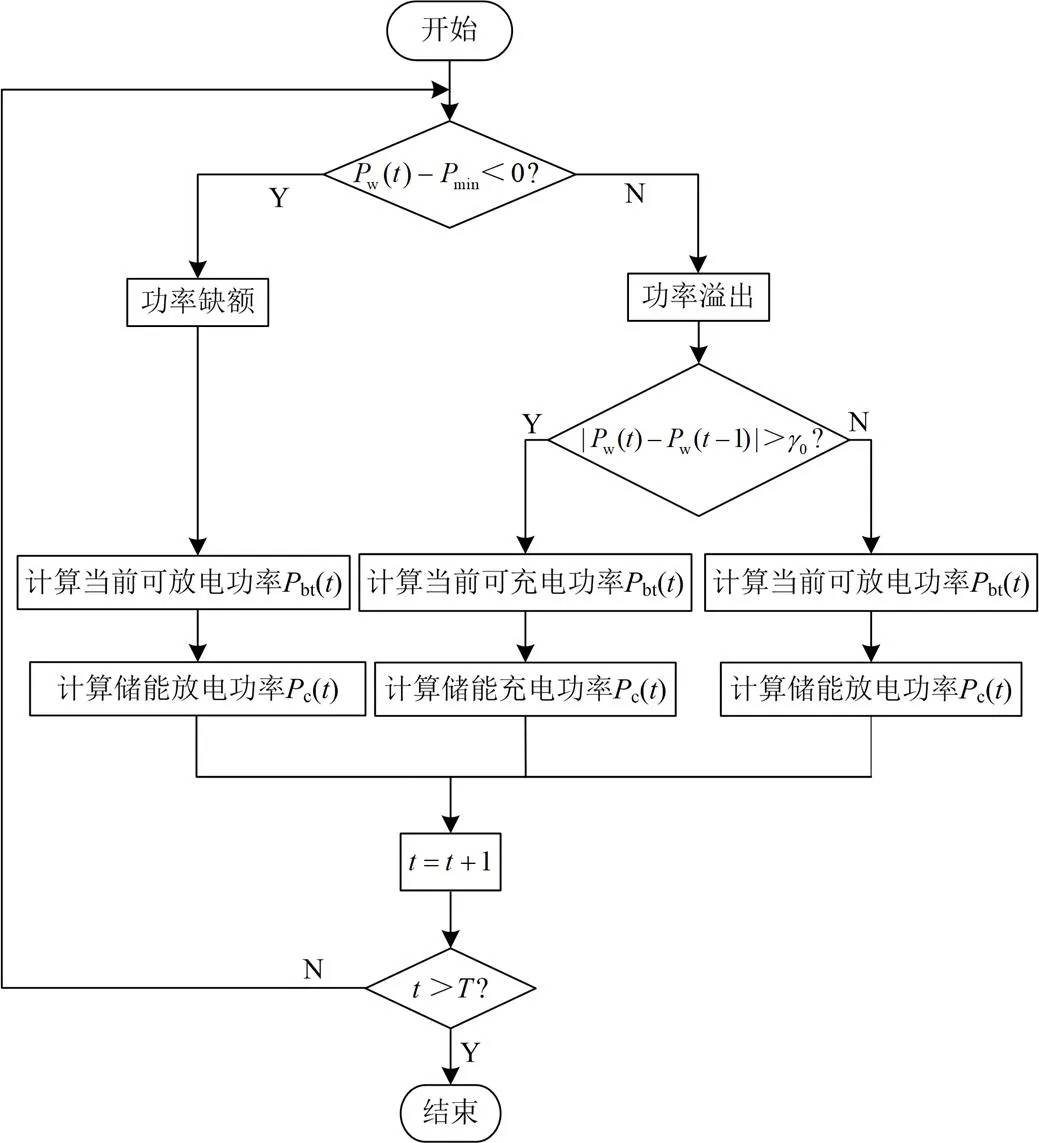
图2 储能运行策略图

储能在黑启动中主要是补偿被启动机组和风电出力之间的缺额。根据风电场输出功率与辅机需求功率的差值，本文提出针对黑启动过程中不同情况下的储能运行策略。当风电功率无法满足黑启动需求功率时，储能进行放电补偿；当风电功率溢出时，在保证黑启动的前提下，储能进行平抑功率波动，使得溢出功率可以向其他负荷输送功率，提升风电和储能利用率。

储能的充放电功率由储能SOC和前一个时刻的容量决定，SOC直接反应储能当前的剩余能量状态，所以必须对每个时刻的SOC进行计算，使SOC始终在正常范围内，确保储能支撑风电厂完成整个黑启动过程。计算公式为

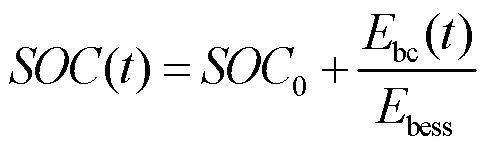
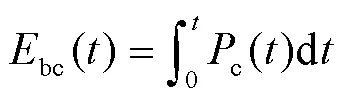
由于补偿的功率不能超越储能当前的剩余功率，所以必须要计算储能当前时刻的可充放功率，计算公式为

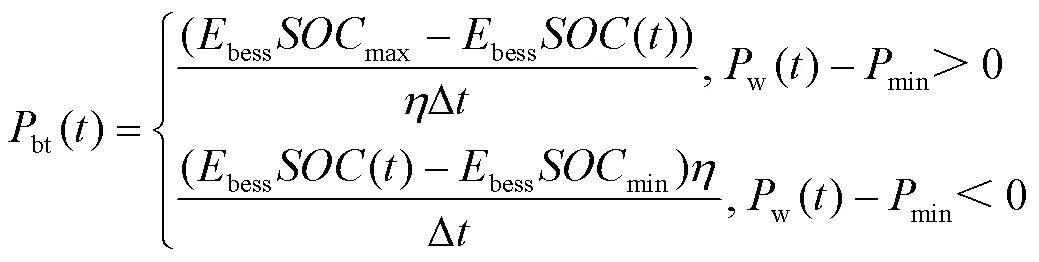
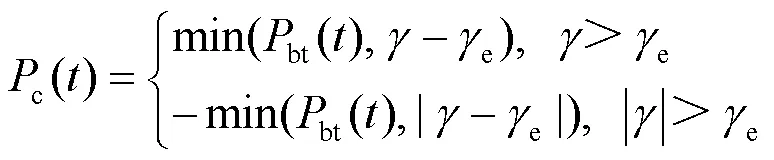
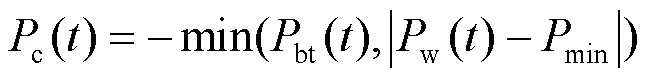
总之，储能补偿功率缺额控制策略概括如下：根据式(9)—式(12)确定当前储能的可释放功率大小，确保储能当前有充足的容量，然后储能输出功率补偿缺额；否则储能无法补偿缺额，将导致黑启动失败。

风电功率溢出时，储能平抑风电波动的控制策略概括如下：当前时刻风电出力大于前一时刻的风电出力，并超过波动上限时，根据式(9)—式(11)确定储能当前可充电功率，储能进行充电；当风电出力小于前时刻的风电出力，并超出波动下限时，根据式(9)—式(11)确定储能当前可放电功率，储能进行放电。

2.3 储能配置优化模型

在确定黑启动可执行时段的基础上，考虑储能运行策略对储能容量配置的影响，以及验证储能运行策略的可行性，研究黑启动储能容量配置。由于整个过程主要是为了保证黑启动的安全运行，考虑黑启动过程中风电功率小于辅机功率的缺额状态，在储能能够补偿缺额功率的情况下，当风电功率溢出时，储能进行平抑风电功率波动，构建优化模型。

2.3.1目标函数

基于前文描述的储能运行策略，考虑黑启动实施要求和平抑波动要求，由于风储黑启动过程中功率及容量需求都远大于平抑波动需求功率及容量，整个过程主要是保证黑启动能安全运行，因此，以最大化补偿缺额功率为目标，确定储能的额定功率和额定容量。

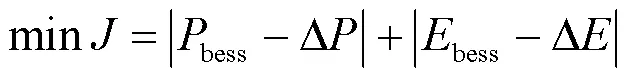
最大功率缺额可表示为

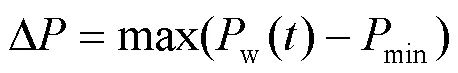
容量可表示为

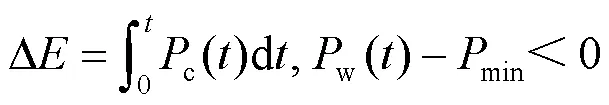
2.3.2约束条件

1) 储能额定功率约束

为了使储能成本减少，考虑到储能作用主要是补偿黑启动过程中的功率缺额以及平抑风电出力波动，而黑启动过程中的功率缺额远大于平抑功率波动差值。所以功率约束采用风电场出力和储能之间的最大缺额功率，其公式为

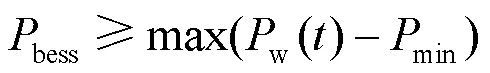
2) 储能额定容量约束

考虑到储能的充放电效率和备用容量，额定容量约束为

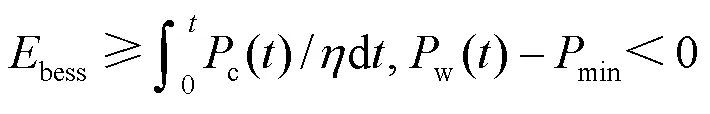
3) 储能SOC约束

为了确保储能长时间的运行，储能必须在合理的SOC区间工作，约束为

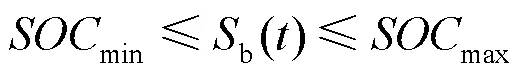
4) 储能充放电功率约束

储能的充放电功率必须小于额定功率，即

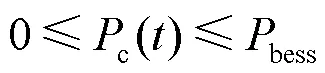
2.4 储能配置方法求解

首先，基于风电场的历史出力数据，利用风电预测算法确定未来1 h的出力，结合被启动火电机组辅机的需求功率，判断当前时间段的黑启动可行性。其次，根据已知的启动时间段风电场预测出力、辅机需求功率、储能运行策略进一步确定储能额定功率和额定容量。最后，对风储系统下达黑启动指令，恢复火电机组运行，进而恢复停电地区供电。整体储能配置方法如图3所示。。

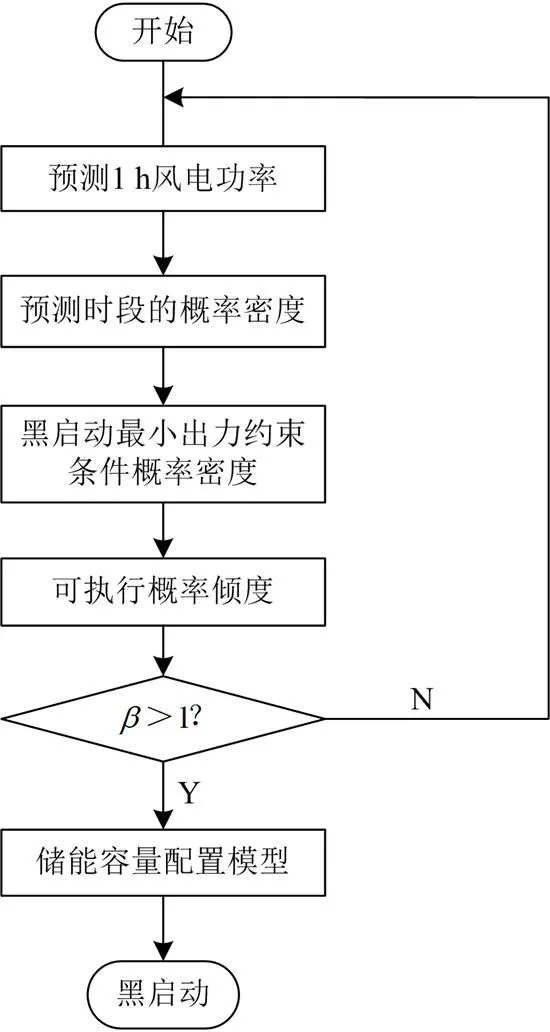
图3 储能配置流程图

由于风电不同时间出力不同，并不是任何时间都可以进行黑启动。本文基于非参数核密度估计建立未来1 h的风电出力概率密度，进而提出满足黑启动最小出力约束的条件概率密度，得出黑启动的可执行倾度，确定启动时间段。并结合储能运行策略以及黑启动功率约束，以最大化补偿缺额功率为目标函数建立储能优化配置模型。由于所提储能配置是双变量和多约束的问题，利用改进粒子群算法进行优化求解，确定黑启动时的储能额定功率和额定容量。

3 算例分析

3.1 黑启动时段确定

基于风电历史数据，利用长短期记忆网络对未来1 h的风电出力进行预测，预测结果如图4所示。预测结果和实测值变化趋势基本一致，预测值与实际值误差率为6%，满足规定的预测误差范围。不同时间段风电出力相差很大，合理选择黑启动的启动时间可以提高黑启动的成功率，间接减少需要的储能容量，因此确定黑启动时段是十分必要的。

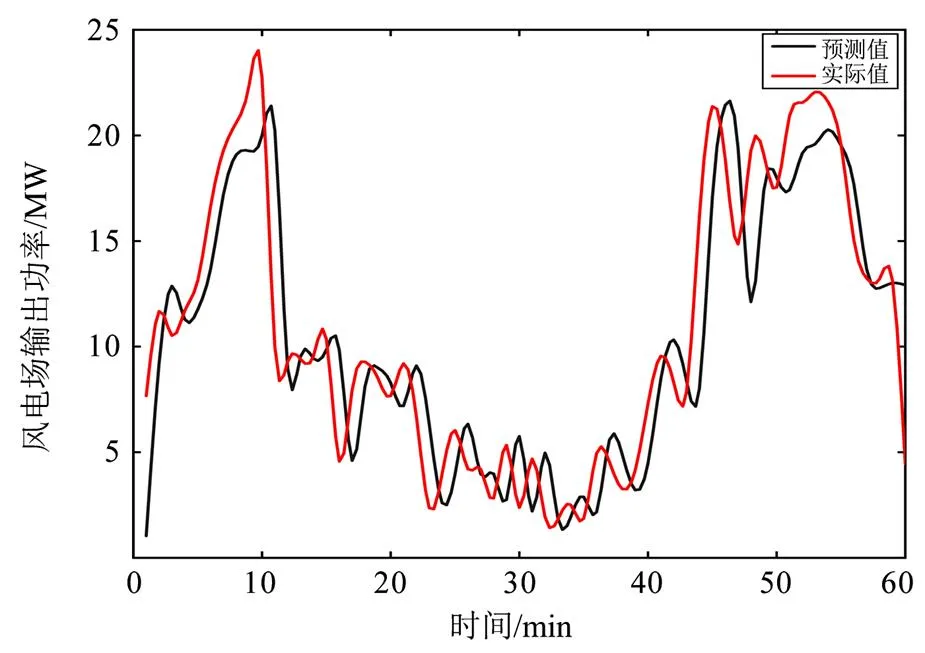
图4 1 h风电出力预测图

火电机组的黑启动至少需要1 h，所以以1 h为一个时间段，基于历史同期数据对未来不同时间段的风电出力进行预测。图5—图7为不同时间段的黑启动最小风功率概率密度和预测的风电出力图。由图可知，时段1和时段3的风电出力满足黑启动最小出力时间太短，时段2的风电出力满足黑启动最小出力时间较长，从对应的概率密度图可知，时段1和时段3满足黑启动最小出力的概率密度较小，时段2满足黑启动最小出力的概率密度较大，基于核密度估计的概率密度可以反映风电场的出力情况，进一步也反映了风电场在不同时间段的黑启动能力，由此可得出不同时间段风电场的黑启动能力相差很大。

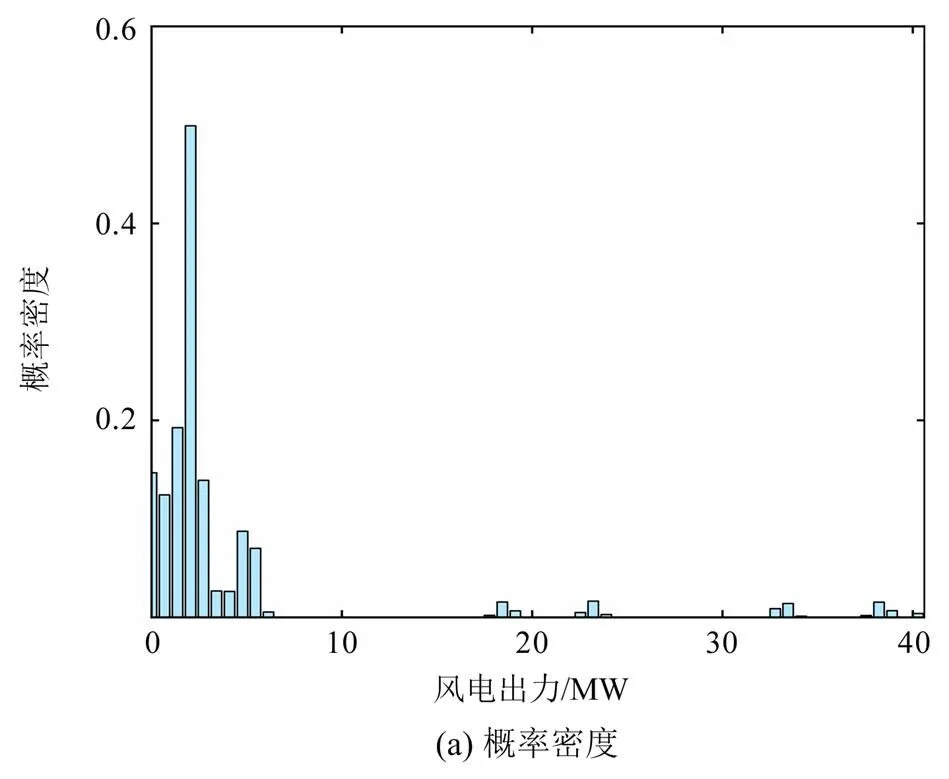
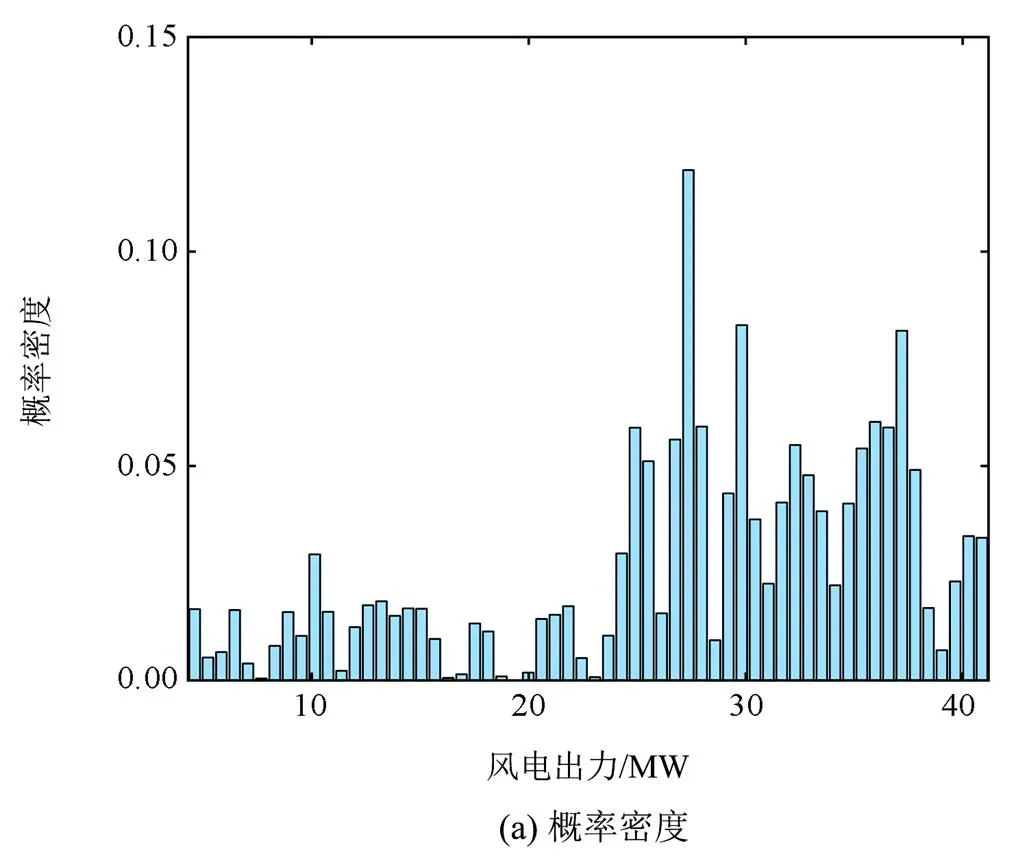
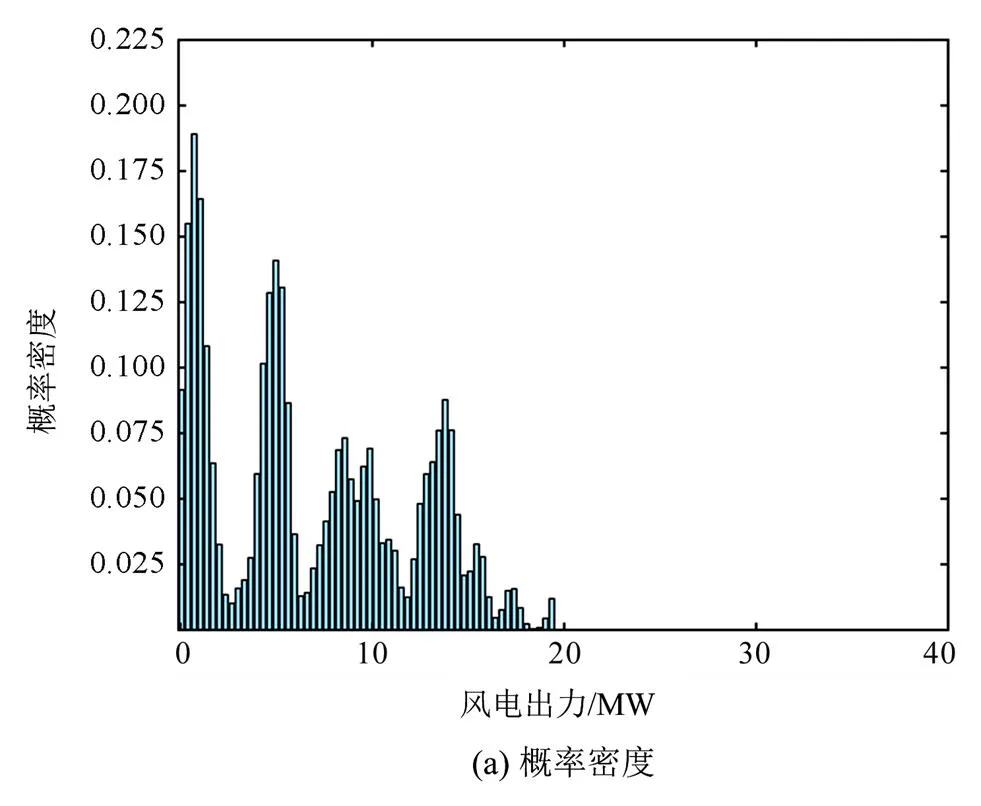
根据式(5)—式(7)可得出各个时间段满足黑启动最小出力的条件概率密度和可执行黑启动的概率倾度，如表1所示。在时段2风电出力满足最小黑启动时间较长，可执行黑启动概率倾度大于1，可执行黑启动。而时段1和时段3可执行黑启动概率倾度小于1，不能执行黑启动。

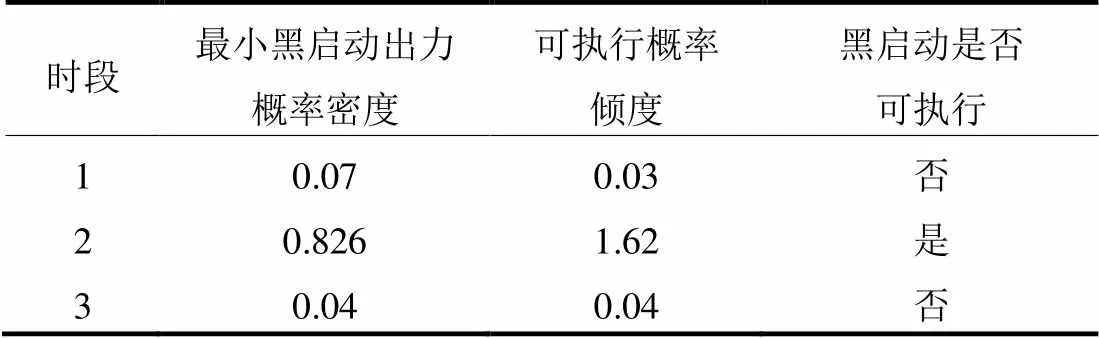
表1 不同时间段黑启动可行性对比

由上述分析可知，利用非参数核密度估计生成的概率密度图像充分反映了风电出力情况，基于最小黑启动出力的条件概率密度得出的黑启动可执行倾度，能够合理地判断能否执行黑启动并确定黑启动可执行时段，使得储能更好地配合风电场实现黑启动运行。

3.2 储能功率和容量的确定

本文采用改进的粒子群算法对储能优化配置模型进行求解，首先分析改进的粒子群算法在不同参数下的敏感度，这里主要分析不同迭代次数和种群数对储能补偿黑启动功率缺额结果的影响。在图8(a)中，迭代次数为100，种群数为50；图8(b)中，迭代次数为500，种群数为100；图8(c)中，迭代次数为2000，种群数为100，其他参数相同，最终得出储能出力结果。在图8(a)的情况下，在0～10 min内储能输出功率小于图8(b)与图8(c)的情况，在后面的分析中可知，在图8(b)的情况下可满足黑启动功率需求，图8(a)的情况无法满足黑启动功率缺额需求。在图8(b)与图8(c)的情况下，结果基本相同，最终确定改进粒子群算法具体参数如下：最大迭代次数为500，种群数量为100，学习因子取为2，杂交概率为0.8，变异概率为0.01。根据上文提到的运行策略，以1 h为一个调度周期，每个周期为60个数据，对黑启动过程中风电出力与被启动负荷的差值进行补偿，功率溢出时储能平抑风电功率波动。最终得到满足黑启动的风电场储能额定功率及额定容量分别为12.9 MW和10.3 MWh。

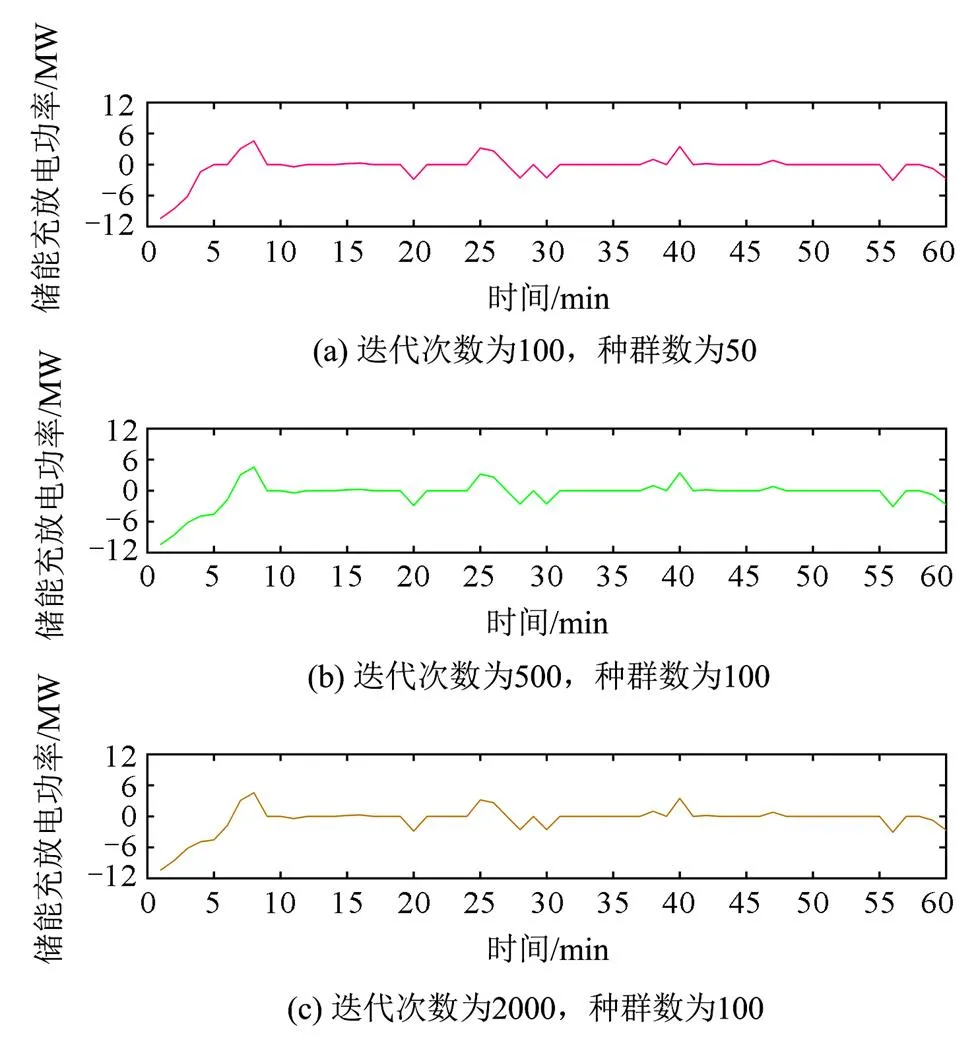
图8 不同参数下储能出力图

为了验证储能运行策略的可行性，补偿及平抑波动效果对比如图9所示，黑启动缺额功率可以由储能稳定补偿，功率溢出时平抑功率波动，最大功率波动为3.48 MW，达到平抑波动率的目的，所提出的运行策略可以满足黑启动的缺额功率要求和波动率要求。图10为整个黑启动过程中的SOC变化曲线图，可知整个黑启动过程中SOC保持在正常的工作区内，保证储能不因SOC越限而导致黑启动失败，同时也延长了储能的使用寿命。

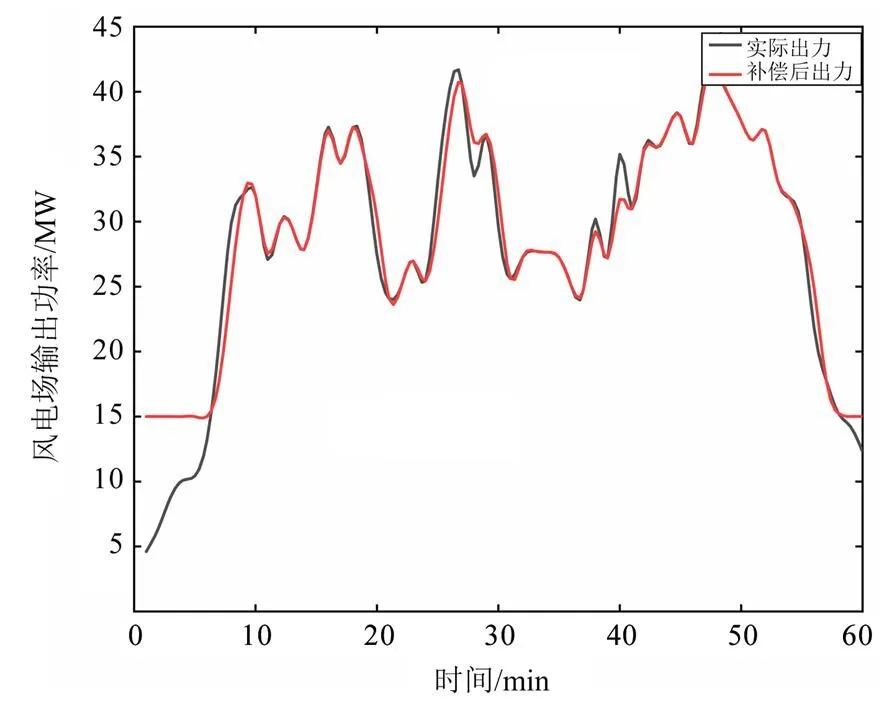
图9 补偿及平抑波动效果对比图

图10 黑启动过程SOC变化图

采用与文献[22]相同的储能类型和单位成本，由表2可知，本文方法风电场的投资成本占比与文献[23]相同，但文献[22]并没有考虑储能自身的相关因素和运行策略的影响，且本文采用的风电场容量更小。所以本文所提方法可以满足黑启动功率平衡，且当风电功率溢出时，满足其他用电需求，进一步提升黑启动过程中的风电利用率，减少黑启动过程中限电弃风。

表2 储能配置与投资成本对比

4 结语

本文针对风储系统黑启动，首先确定风电场黑启动时段，考虑了补偿黑启动功率缺额以及平抑风电功率波动，以最大化补偿功率缺额为目标，提出了支撑风电场黑启动的储能配置方法，得出以下结论。

1) 利用长短期记忆网络算法并结合核密度估计对风电场未来1 h内出力进行概率密度建模，然后根据定义的满足黑启动最小出力条件概率密度，进一步确定黑启动可执行倾度，判断未来时段风电场的黑启动可行性，确定黑启动时段，保证黑启动过程的功率需求，最终确定时段2为黑启动可执行时段。

2) 结合储能运行策略，提出以最大化补偿功率缺额为目标的储能容量配置模型，并通过改进粒子群算法对优化模型进行求解，得出储能额定功率为12.9 MW，额定容量为10.3 MWh，可以满足黑启动的功率需求。

3) 通过分析表明，所提运行策略可以在功率缺额状态时补偿功率缺额，平抑波动状态下可保证风电出力波动率在10%以内，最终储能成本占风电场投资成本的11%左右，同时可以保证黑启动的正常运行。

[1] 李保杰, 李进波, 李洪杰, 等. 土耳其“3.31”大停电事故的分析及对我国电网安全运行的启示[J]. 中国电机工程学报, 2016, 36(21): 5788-5795.

LI Baojie, LI Jinbo, LI Hongjie, et al. Analysis of Turkey's "3.31" blackout and its enlightenment to the safe operation of China's power grid[J]. Proceedings of the CSEE, 2016, 36(21): 5788-5795.

[2] 胡秦然, 丁昊晖, 陈心宜, 等. 美国加州2020年轮流停电事故分析及其对中国电网的启示[J]. 电力系统自动化, 2020, 44(24): 11-18.

HU Qinran, DING Haohui, CHEN Xinyi, et al. Analysis of alternating blackouts in California in 2020 and its enlightenment to China's power grid[J]. Automation of Electric Power Systems, 2020, 44(24): 11-18.

[3] 刘玉田, 王洪涛, 叶华. 电力系统恢复理论与技术[M]. 北京: 科学出版社, 2014.

[4] 顾雪平, 李新军, 杨超, 等. 考虑风电参与的黑启动方案[J]. 电力自动化设备, 2020, 40(1): 31-37.

GU Xueping, LI Xinjun, YANG Chao, et al. Black start scheme considering wind power participation[J]. Electric Power Automation Equipment, 2020, 40(1): 31-37.

[5] PATSAKIS G, RAJAN D, ARAVENA I, et al. Optimal black start allocation for power system restoration[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6766-6776.

[6] LI J, YOU H, QI J, et al. Stratified optimization strategy used for restoration with photovoltaic-battery energy storage systems as black-start resources[J]. IEEE Access, 2019, 7: 127339-127352.

[7] LEHTOLA T, ZAHEDI A. Solar energy and wind power supply supported by storage technology: a review[J]. Sustainable Energy Technologies and Assessments, 2019, 35: 25-31.

[8] BULLICH-MASSAGUÉ E, CIFUENTES-GARCÍA F J, GLENNY- CRENDE I, et al. A review of energy storage technologies for large scale photovoltaic power plants[J]. Applied Energy, 2020, 274.

[9] 孙伟卿, 罗静, 张婕. 高比例风电接入的电力系统储能容量配置及影响因素分析[J]. 电力系统保护与控制, 2021, 49(15): 9-18.

SUN Weiqing, LUO Jing, ZHANG Jie. Energy storage capacity allocation and influence factor analysis of a power system with a high proportion of wind power[J]. Power System Protection and Control, 2021, 49(15): 9-18.

[10] FENG Q, WANG J, CHEN C, et al. Optimal black start resource allocation[J]. IEEE Transactions on Power Systems, 2016, 31(3): 2493-2494.

[11] FENG L, ZHANG J, Li G, et al. Cost reduction of a hybrid energy storage system considering correlation between wind and PV power[J]. Protection and Control of Modern Power Systems, 2016, 1(2): 86-94.

[12] LIU L, WU J, MI Z, et al. A feasibility study of applying storage-based wind farm as black-start power source in local power grid[C] // 2016 International Conference on Smart Grid and Clean Energy Technologies (ICSGCE), October 19-22, 2016, Chengdu, China: 257-261.

[13] GUO T, LIU Y, ZHAO J, et al. A dynamic wavelet-based robust wind power smoothing approach using hybrid energy storage system[J]. International Journal of Electrical Power & Energy Systems, 2020, 116.

[14] 桑丙玉, 姚良忠, 李明杨, 等. 基于二阶锥规划的含大规模风电接入的直流电网储能配置[J]. 电力系统保护与控制, 2020, 48(5): 86-94.

SANG Bingyu, YAO Liangzhong, LI Mingyang, et al. Research on energy storage system planning of DC grid with large-scale wind power integration[J]. Power System Protection and Control, 2020, 48(5): 86-94.

[15] 赵伟, 袁锡莲, 周宜行, 等. 考虑运行寿命内经济性最优的梯次电池储能系统容量配置方法[J]. 电力系统保护与控制, 2021, 49(12): 16-24.

ZHAO Wei, YUAN Xilian, ZHOU Yixing, et al. Capacity configuration method of a second-use battery energy storage system considering economic optimization within service life[J]. Power System Protection and Control, 2021, 49(12): 16-24.

[16] WU T, SHI X, LIAO L, et al. A capacity configuration control strategy to alleviate power fluctuation of hybrid energy storage system based on improved particle swarm optimization[J]. Energies, 2019, 12(4).

[17] CHEN L, ZHANG X, HAN P, et al. Optimization of SMES-battery hybrid energy storage system for wind power smoothing[C] // 2020 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), October 16-18, 2020, Tianjin, China.

[18] PANG M, SHI Y, WANG W, et al. Optimal sizing and control of hybrid energy storage system for wind power using hybrid Parallel PSO-GA algorithm[J]. Energy Exploration & Exploitation, 2019, 37(1): 558-578.

[19] 周宜昌, 刘艳, 顾雪平. 考虑多风电场黑启动价值的机组恢复顺序双层优化决策[J]. 电力系统自动化, 2020, 44(16): 87-97.

ZHOU Yichang, LIU Yan, GU Xueping. Double level optimization decision of unit recovery sequence considering black start value of multiple wind farms[J]. Automation of Electric Power Systems, 2020, 44(16): 87-97.

[20] 杜康, 刘艳, 叶茂, 等. 辅助风电场参与初期黑启动时储能电站容量配置策略[J]. 电力系统保护与控制, 2017, 45(18): 62-68.

DU Kang, LIU Yan, YE Mao, et al. Capacity allocation strategy of energy storage power station when auxiliary wind farm participates in initial black start[J]. Power System Protection and Control, 2017, 45(18): 62-68.

[21] 李翠萍, 张世宁, 李军徽, 等. 风储系统作为黑启动电源的容量配置策略[J]. 电力系统保护与控制, 2021, 49(3): 88-95.

LI Cuiping, ZHANG Shining, LI Junhui, et al. Capacity allocation strategy of wind storage system as black start power supply[J]. Power System Protection and Control, 2021, 49(3): 88-95.

[22] 刘威鹏, 刘玉田. 基于非对称Copula函数的风电场黑启动储能优化配置[J]. 电力系统自动化, 2020, 44(19): 47-54.

LIU Weipeng, LIU Yutian. Optimal allocation of wind farm black start energy storage based on asymmetric copula function[J]. Automation of Electric Power Systems, 2020, 44(19): 47-54.

[23] 米增强, 孙朝阳, 刘力卿, 等. 储能型风电场作为黑启动电源时电池储能系统的配置方法[J]. 电测与仪表, 2018, 55(12): 20-26.

MI Zengqiang, SUN Chaoyang, LIU Liqing, et al. Configuration method of battery energy storage system when energy storage wind farm is used as black start power supply[J]. Electrical Measurement & Instrumentation, 2018, 55(12): 20-26.

[24] LI C, ZHANG S, ZHANG J, et al. Method for the energy storage configuration of wind power plants with energy storage systems used for black-start[J]. Energies, 2018, 11(12).

[25] 杨楠, 崔家展, 周峥, 等. 基于模糊序优化的风功率概率模型非参数核密度估计方法[J]. 电网技术, 2016, 40(2): 335-340.

YANG Nan, CUI Jiazhan, ZHOU Zheng, et al. Non- parametric kernel density estimation method of wind power probability model based on fuzzy order optimization[J]. Power System Technology, 2016, 40(2): 335-340.

[26] 马兰, 谢丽蓉, 叶林, 等. 多目标多工况双储能协同运行策略[J]. 电力系统自动化, 2021, 45(20): 38-48.

MA Lan, XIE Lirong, YE Lin, et al. Cooperative operation strategy of dual energy storage under multiple objectives and multiple operation conditions[J]. Automation of Electric Power Systems, 2021, 45(20): 38-48.

Optimal configuration of wind farm black start energy storage capacity:a method considering energy storage operation strategy

YAN Laiqing, CAO Liyuan, XUE Tailin, ZHANG Xuejun, WANG Qi

(School of Electric Power, Civil Engineering and Architecture, Shanxi University, Taiyuan 030006, China)

The proportion of wind power in the regional power grid is increasing. To solve the problem of wind power output fluctuation during the black start process of wind farms, an energy storage configuration method with an energy storage operation strategy is proposed. First, the predicted power is obtained based on a wind power prediction algorithm, and the minimum black-start output probability density and the black-start executable probability inclination are defined by non-parametric kernel density estimation. Then the black-start period is determined. Secondly, the energy storage operation strategy is formulated with the role of energy storage in compensating for power shortage and suppressing fluctuations during the black start process. For the influence of energy storage operation strategy on capacity allocation, taking the rated power and capacity of energy storage as model independent variables, an energy storage optimal allocation model with the maximization of compensation power shortage as the objective function is established. The improved particle swarm optimization algorithm is used to analyze the model. Finally, the data of a 45 MW wind farm in Inner Mongolia verifies the feasibility of the energy storage operation strategy and optimal configuration model.

black start; non-parametric kernel density estimation; probability density; energy storage operation strategy; energy storage capacity configuration

10.19783/j.cnki.pspc.211420

This work is supported by the Youth Fund of Basic Research for Application in Shanxi Province (No. 20210302124553).

山西省应用基础研究计划青年项目资助(20210302124553)

2021-10-23；

2022-03-03

闫来清(1983—)，男，博士，硕士生导师，主要研究方向为电力系统数据驱动建模方法与控制、储能系统运行与控制；E-mail: yanlq@sxu.edu.cn

曹丽源(1996—)，男，通信作者，硕士研究生，主要研究方向为新能源参与黑启动的储能优化配置与控制；E-mail: 1195678058@qq.com

薛太林(1965—)，男，教授，硕士生导师，主要研究方向为电力数据监测与挖掘、配电网新能源规划。E-mail: 13803434745@163.com

(编辑 许 威)