线性工程中优化选择独立坐标系的应用研究

杨宝宏

(中陕核工业集团测绘院有限公司，陕西 西安 710024)

1 引 言

在线性工程设计和施工阶段往往由于投影变形的影响不能直接使用现行的2000国家大地坐标系，尤其是在我国西部山区，实施线性工程测绘工作时，必须要考虑建立科学的、便于施工且满足规范要求的独立坐标系，同时与2000国家大地坐标系建立联系。实际应用中，首先需要明晰本工程项目的地理位置特点，规范允许的最大限度投影变形值，综合分析高程归化和高斯投影两者产生边长投影变形的规律和特点，利用两者规律和特点优化选择最适合的中央子午线和投影面来确定平面坐标系。本文结合在实际工作中参与的相关项目，分析投影变形的规律和特点，探讨优化选择线性工程平面控制测量坐标系的方法研究。

2 规范要求

不同类别的线性工程，在相关测量规范中都对边长投影变形做了要求，各类工程的精度要求不同，投影变形限度也不同。

公路工程，根据文献[1]“选择路线平面控制测量坐标系时，应使测区内投影长度变形值不大于 2.5 cm/km；大型构造物平面控制测量坐标系，其投影长度变形值不应大于 1 cm/km。投影分带位置不应选择在大型构造物处。”

高铁工程，根据文献[2]“高速铁路工程测量平面坐标系应采用工程独立坐标系统，在对应的线路轨面设计高程面上坐标系统的投影长度变形值不宜大于 10 mm/km。”

水利水电工程，根据文献[3]“大比例尺地形测绘，长度投影变形值不应大于 5 cm/km。”

油气输送管道工程，根据文献[4]“除线路工程外，平面控制测量测区内投影长度的变形值不应大于 2.5 cm/km。”

3 边长投影变形

边长的投影变形由两部分组成，分别为实测边长(加倾斜改正后)归算到椭球面变形、椭球面边长归算到高斯平面的变形，这两个步骤称为高程归化和高斯投影，两者的变形影响一正一反，具有一定的补偿性。

3.1 高程归化改正

(1)

式中：Hm—归算边高出椭球面的平均高程；

R—归算边方向法截弧曲率半径；

S—归算边长度；

△S1—高程归化改正值。

以1 km边长为例，高程变化与高程归化改正量为线性变化关系，如图1所示。

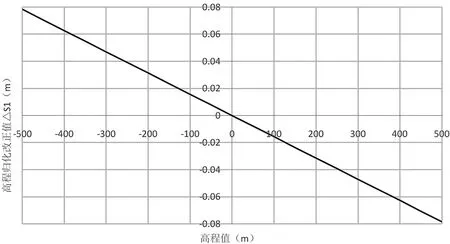
图1 高程归化改正值变化

可见，地面点相对于参考椭球面(投影面)高度超过 64 m，或测区内高差跨度大于 128 m时，高程归化产生的变形影响将超过 1 cm/km；地面点相对于参考椭球面高度超过 160 m，或测区内高差跨度大于 320 m时，高程归化产生的变形影响将大于 2.5 cm/km。

3.2 高斯投影改正

(2)

式中：ym—测距边中点到中央子午线的距离；

R—归算边方向法截弧曲率半径；

S—归算边长度；

△S2—高斯投影改正值。

以1 km边长为例，测距边中心点距离中央子午线的距离与高斯投影改正量呈二次项函数关系，如图2所示。

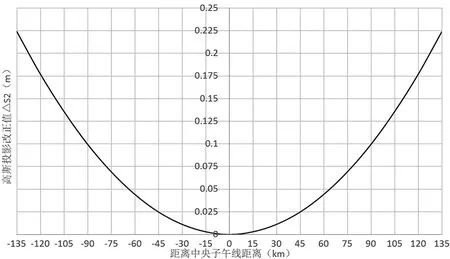
图2 高斯投影改正值变化

可见，当测区内任意边长中心点偏离中央子午线 29 km，高斯投影产生的变形影响将超过 1 cm/km；偏离中央子午线 45 km，高斯投影产生的变形影响将超过 2.5 cm/km。

3.3 综合变形影响

一般情况下，以上两者的改正值一正一负，可以相互抵消，但变化规律不相同，并不能完全得到补偿。

综合改正值：

△S=△S1+△S2

(3)

实际应用中，需分析两者变化趋势，综合考虑选择合适的中央子午线和投影面，来选取坐标系。从而满足关系式：

(4)

可通过改变Hm或ym或同时改变两者的值来确定中央子午线和参考椭球面位置。

4 工程实例

4.1 西藏阿里地区国道565延伸线勘测项目

位于我国西藏高海拔地区，该公路是我国西部边疆公路网重要组成部分，测区自然环境及气候条件恶劣。公路全长 115 km，沿河而建，呈东西走向，横跨高斯投影第26带和第27带。海拔东高西低，起点最大高程 3 650 m，终点最小高程 2 900 m，线路高程变化情况，如图3所示。

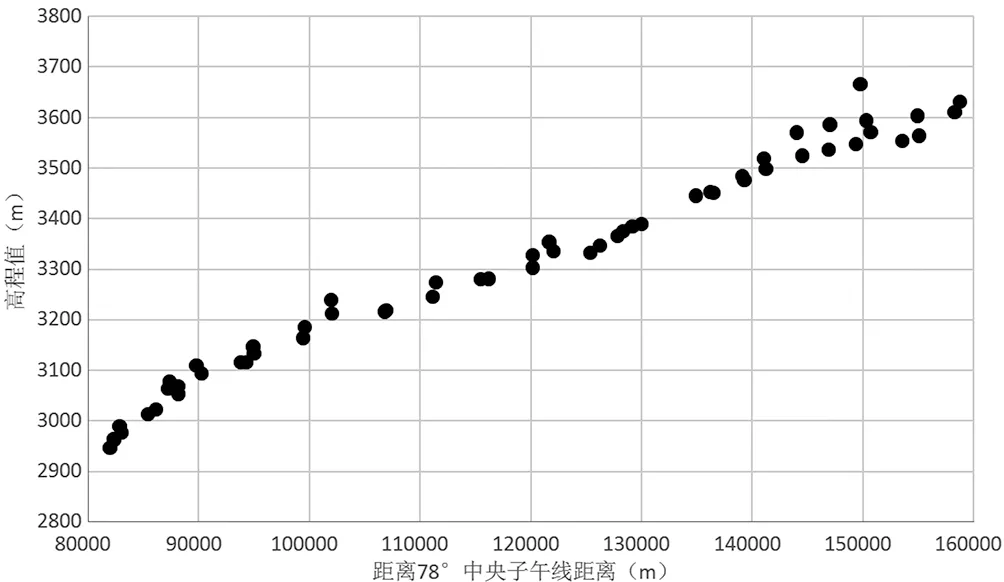
图3 高程变化情况

通过控制测量获得控制点CGCS2000坐标(中央子午线78°)，经计算，综合改正值极值分别为 -25 cm、 -38 cm，自西向东高程归化改正值由 -46 cm变化至 -57 cm，高斯投影改正值由 8 cm变化至 31 cm。前者变化量为 -11 cm，后者变化量为 23 cm。可见，高程归化和高斯投影的改正值，虽然在数值上正负相反，但变化趋势不同、变化量不同，因此，综合改正值并不能得到很好的补偿。如图4所示。

图4 CGCS2000坐标系各项改正值

显然，建立任意带高斯投影坐标系或者抵偿高程面坐标系都不能很好地消化较大的变形值。若采用常规办法，将中央子午线平移至测区内，再选取测区平均高程面作为投影面建立坐标系，为消化东西端 750 m高差产生的投影变形影响，则需要建立3个独立坐标系，而在设计、施工过程中，频繁转换十分不便。

综合分析投影变形规律和该项目中各项改正值的变化趋势，尝试平移中央子午线使高斯投影改正量变化趋势与高程归化改正量变化趋势相反，通过计算，选取测区最西端GN01控制点向西 19 km的位置，该处中央子午线为78°42′，根据式(4)，使ζ=0，计算出投影面高度，最终确定抵偿高程面高出椭球面 3 000 m。选取的抵偿高程面任意带坐标系各项改正值计算结果如图5所示。

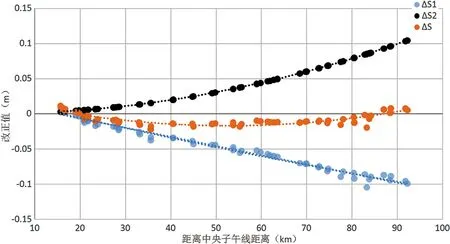
图5 抵偿高程面任意带坐标系各项改正值

计算结果显示，将中央子午线平移至测区最边缘78°42′的位置，并抬高椭球面 3 000 m，建立新的参考椭球，在该坐标系下，综合改正值范围在 -2.2 cm至 1.1 cm区间，完全符合规范要求，很好地补偿了两种变形产生的影响，实现了建立一个独立坐标系，就可以解决全线路 115 km的投影变形影响，优化了常规坐标系的选择方法。

4.2 福银高速公路(G70)西安至永寿段改扩建测量项目

该公路项目起点位于礼泉县西张堡立交，终点为永寿县御驾宫附近，路线全长 50 km，为东南向西北走向，测区高程由起点至终点逐渐升高，如表1所示。

表1 路线起终点坐标成果表(CGCS2000坐标系，中央子午线108°)

该公路虽然距离108°中央子午线较近，但平均高程较大，起终点高差 480 m，高斯投影产生的边长变形较小，高程归化产生的边长变形较大，经计算，综合改正值极值分别为 -4.7 cm和 -14.8 cm，均超过 2.5 cm范围，不能直接采用CGCS2000坐标系供设计及施工使用，如图6所示。

图6 CGCS2000坐标系各项改正值

计算结果显示，高程归化改正值自东向西由 -7.6 cm变化至 -15.1 cm，变化量为 -7.5 cm，若将中央子午线选取在测区范围内，虽然降低了高斯投影变形的影响，但无论如何选取参考椭球面都无法通过建立一个坐标系来消化这 -7.5 cm的变化量。

结合高斯投影长度变形特点，将高斯投影长度变形放大，利用高斯投影变形来抵消高程归化产生的变形。平移中央子午线至远离测区的位置，使得高斯投影改正值的变化量接近 7.5 cm。经计算，选择距离测区边缘点GN01控制点 74 km的位置，中央子午线为109°20′。此时，恰好无须重新选择投影面，两者变化趋势基本相同，综合改正值均在 2.5 cm范围内，如图7所示。

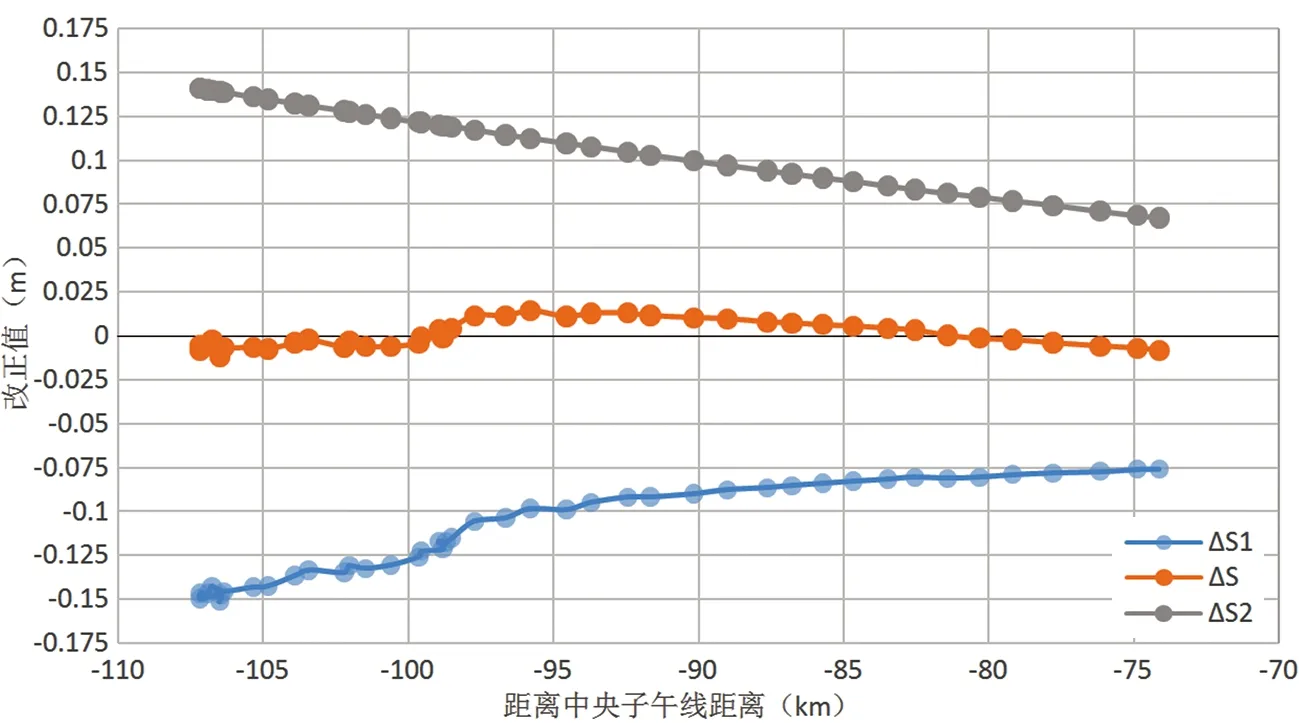
图7 任意带坐标系各项改正值

通过选择一个任意带坐标系，无须选取高程抵偿面，解决了投影长度变形的问题，坐标成果计算也较为容易了。既符合规范要求，又优化了常规处理方法，避免建立两个独立坐标系带来的不便。

5 结 语

不同精度要求的线性工程，常见的投影变形最大限度取值有 1 cm/km、2.5 cm/km、5 cm/km，根据不同工程要求，可选择的独立坐标系有很多，但同一工程项目过多的选取坐标系会给实际工作带来很大不便，精度也不高，还会降低工作效率。分析投影变形规律，结合实际项目的特点，通过数据计算，利用投影变形产生的原理和规律特点优化选择最合适的中央子午线和投影面，是实施整个工程质量前提保障。