里必区块煤层气多分支水平井井型优化

刘升贵LIU Sheng-gui；周东旭ZHOU Dong-xu

（中国矿业大学（北京），北京 100083）

0 引言

煤层气是一种储存在煤层中的非常规天然气[1]，其形成过程主要为随着煤化作用的不断进行，稠环芳香烃体系中的多种侧链和官能团（羟基-OH、甲氧基-OCH3、羧基-COOH、甲基-CH3、醚基-O-、羰基=C=O 等）不断发生断裂和脱落，数量不断减少，从而形成各种挥发性产物，如CO2，H2O、CH4等气体逸出，从而形成的煤层气。所以煤层气既是生成层，又是存储层[2]煤层气的开采主要是通过排水采气，打破煤层气原有的吸附态，使之变为游离态从而排出[3-6]，因此煤层气井至关重要。我国是煤层气资源大国，埋深2000m 以内的储量达到了36.8×1012m3。但我国煤储层条件不好，大都属于高压、低渗、大埋深煤层，开发技术要求高，煤层气井失稳情况严重。煤层气井失稳的影响巨大，可能引起井筒坍塌、缩径和破裂等问题，而井壁维护的成本又很高。由此，对煤层气井稳定性的研究十分必要。

在前人的研究中，有人从二维裂隙模型或三维单分支井模型出发研究井壁稳定性，如孙正财、刘向君等采用数值模拟的方法研究了井底压力、井径和割理密度等因素对井壁稳定性的影响，并给出了其一般规律[7]；或对井壁失稳机理进行理论分析，比如早在1940 年，H.M Wwstergard 发表了第一篇关于井壁稳定性的文章，假设水平应力与垂直应力相等，液柱压力为0，对直井围岩进行了弹塑性力学分析[8]。或进行力化耦合的讨论，如M.E.Chenevert 对泥浆体系的流动性，并进行了力学试验，尝试解决斜井失稳的问题[9]。本文从此出发，建立不同的井筒模型，结合实际工程情况，对多分支水平井进行流固耦合的模拟，对比之后得到最优解。

1 工程背景

1.1 区块内多分支井产气概况

里必区块内部共有126 口煤层气井，其中丛式井93口，单分支水平井33 口，多分支水平井仅有一口。在原开发计划中，里必区块内将开发3 口多分支井，但在钻第一口时，因井壁失稳情况严重被紧急叫停，后改为单分支井，且正在工作的多分支井也产气效率低下，其日产气量对比如图1 所示。

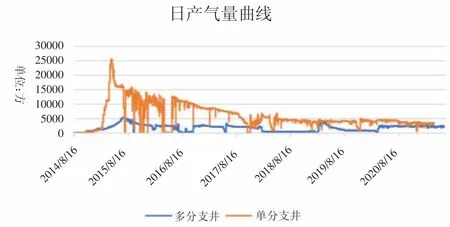
图1 产气量曲线对比图

图中为多分支水平井与临近的单分支水平井日产气量曲线对比，我们可以看出二者差距巨大。多分支井不仅产气量低下，而且产气不稳定。正常情况下多分支井产气稳定后的日产气量应为单分支的数倍。由此我们可以推断出，该多分支井井下失稳情况严重。

1.2 多分支井工程设计情况

该多分支井位于里必区块中部，地面海拔885m,设计井深1815m，水平段进尺4500m，属于大埋深煤层。从井型上看，该井属于单主支多分支水平井。其井身结构如图2、图3 所示。

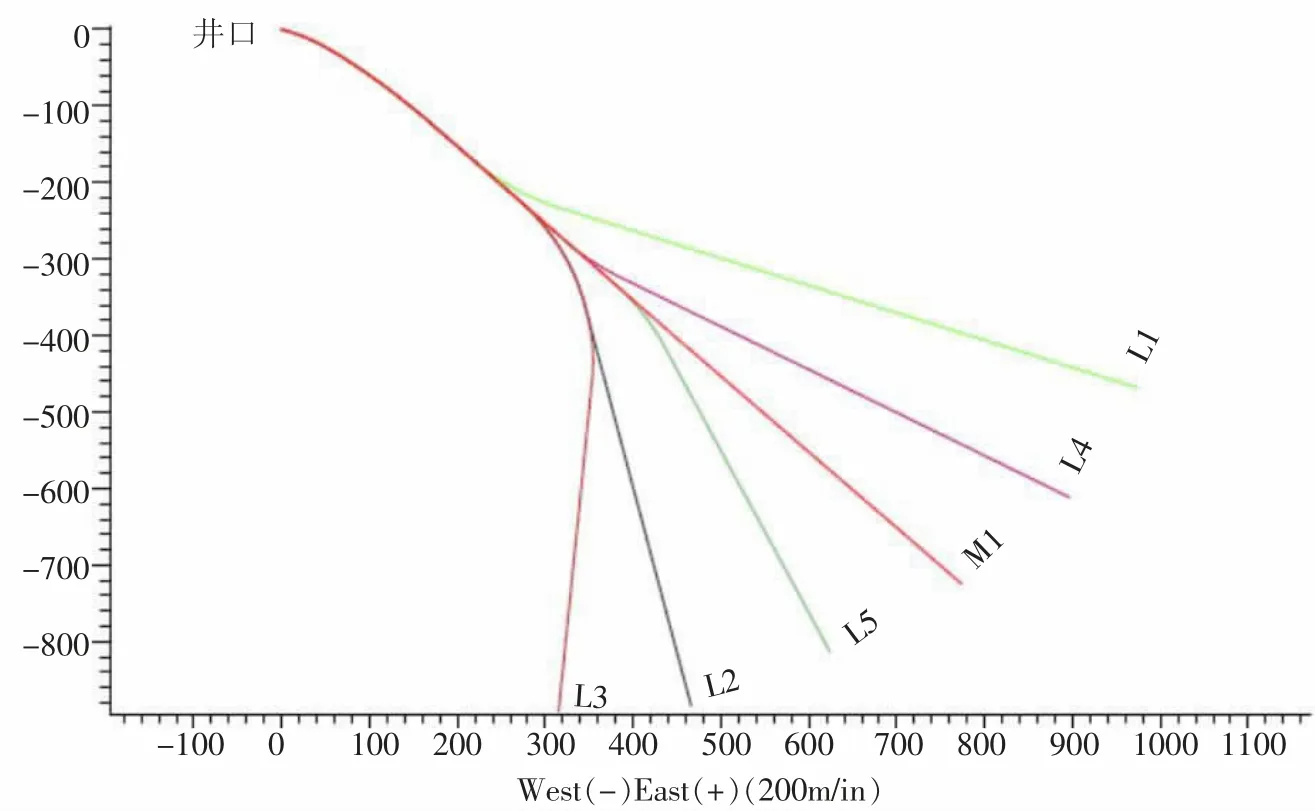
图2 多分支井俯视图

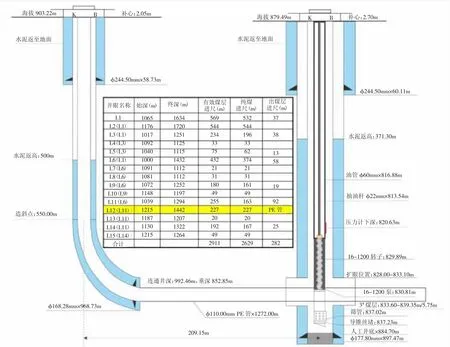
图3 多分支井井身结构

该多分支井完井方式为直井段套管完井，水平井段仅部分采用PE 套管完井。该井型的优点是：采用直井和水平井近距离对接的双井筒结构，水平段采用单主支，这种大密度多分支水平井眼的部署有效缩短了压降路径、改善了导流能力、增加了泄流面积，获得了非常显著的提产效果。缺点是：

分支井过于集中，导致主井、支井夹角处应力集中现象十分严重，极易发生垮塌，该井型较适用于埋深较浅的煤层，对于里必区块内的煤储层条件来说，并不具有适配性。

综上所述，对沁水地区里必区块内部多分支水平井稳定性的分析是十分有必要的。

2 力学模型的建立

2.1 固体力学

文中固体部分的分析以固体力学为基础，由于区块内地下埋深较大，煤层致密，所以不考虑煤岩中的节理系统，分析在线弹性条件下煤岩的应力应变情况，控制方程为：

其中ρ 为密度，da为阻尼系数，~f 为体力。其中~σ 为应力。

2.2 达西定律

其中籽为密度，着是孔隙率，u 是流体速度。公式表达的是渗流过程中的质量守恒。

2.3 失效准则

采用Mohr-Coulomb 准则，其表达式为：

式中，子为临界剪应力；滓n 为垂直于剪切面上的法向正应力（MPa）；C0为材料的粘聚力；渍为材料的内摩擦角。

Mohr-Coulomb 准则只考虑最大和最小主应力的影响，不考虑中间应力的影响[10]，其用最大最小主应力表示为：

3 流固耦合分析

3.1 物理模型的建立

由于在实际工程中，地层数据不可改变，所以本文只讨论工程因素对井壁稳定的影响。文章对井筒模型进行了一定的简化，在保证稳定性规律不变的情况下，使之更符合实际情况。模型中首先改变井型，建立两种双主支多分支水平井与现存的单主支井进行对比，得出更优解后，再进行进一步的井型讨论。为使计算简便，文中对模型取了对称结构。将现有井身简化为如图4 所示。

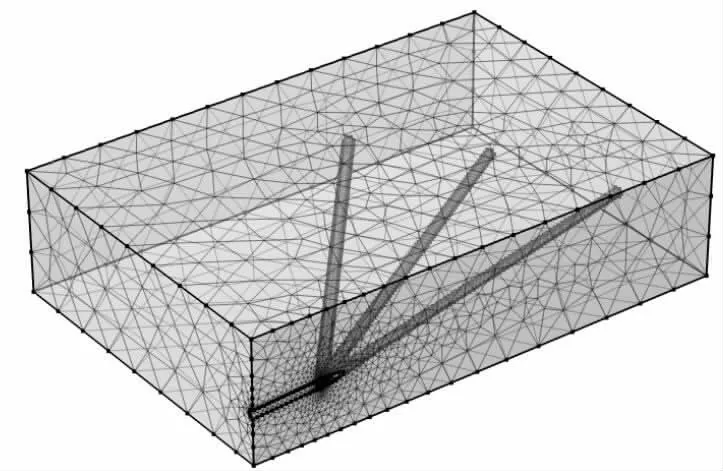
图4 单主支多分支井简化模型

另外建立两种双主支井，模型分析三者之间的相对稳定性问题，建立模型如图5 所示。

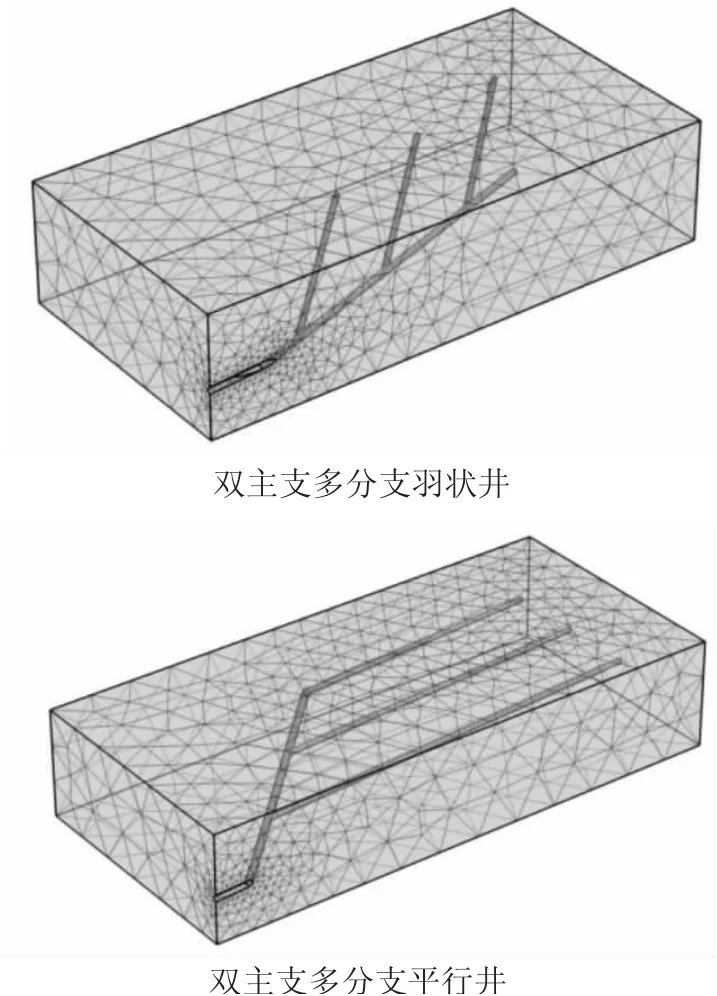
图5 双主支多分支水平井

3.2 模型前处理

所有模拟数据，均取自钻井和测井参数，具体数据如表1 所示。

表1 材料属性

通过钻井及测井工程可以得到，数值模拟的边界条件：地层压力为7.21MPa，煤储层倾角取平均倾角4°，渗透压实测为6.8MPa，又因为多分支水平井处煤层气解吸压力统计为3.8MPa，所以井内流压设置为3MPa。以此为边界条件，进行多孔弹性介质的稳定渗流模拟。

3.3 模拟结果分析

3.3.1 井型对井壁稳定性的影响（图6 所示）

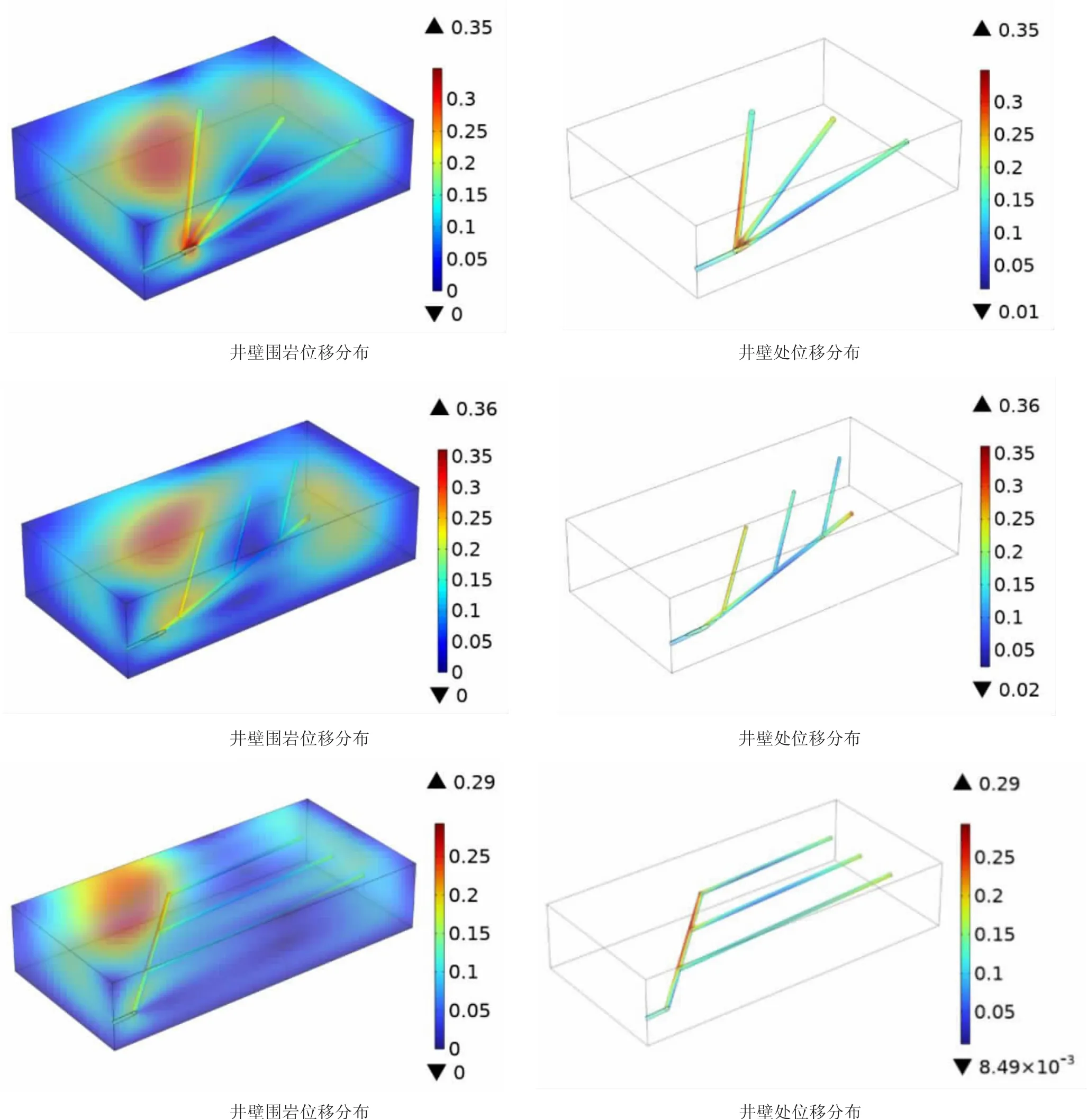
图6 不同井型位移分布情况

首先，对于里必区块内现存的单主支多分支水平井来说，最大位移大于后两者，说明与对比井型来说，现存的更容易失稳。目前单主支井与羽状井比较，最大位移略大，但是相差不多。由于单主支井在同一处钻出多个分支，导致应力集中情况非常严重；另外单主支井分支井进尺相对较大，导致在长井眼轨迹的中部也容易产生较大的位移。与之相比，虽然最大位移相差不大，但是羽状井整体位移分布均匀，应力集中部分相对较小，更有利于井壁的稳定性。与前二者对比，平行井的优势更为明显，最大位移远低于前两种井型，且位移情况分布均匀，在井眼控制范围内很少发生较大位移。除此之外，还存在钻井简单，支撑容易等优点。

另外通过对比Mises 应力的极值大小，也可以发现平行井的Mises 应力的极值最小。而Mises 应力是衡量塑性应变程度的物理量，所以，从最大Mises 应力的角度分析也是平行井的极值更小。利用Mohr-Coulomb 准则进行判定，可以发现三者的最大切应力大小为：单主支井>羽状井>平行井。也可得到相同的结论。

综上所述，双主支多分支平行井更有利于井壁稳定性，后面以此为基础进行进一步分析。

3.3.2 主井夹角对井壁稳定性的影响

主井夹角对煤层气水平井的形态影响巨大，对多分支井井组应力应变的影响是十分显著的，因此我们首先讨论主井夹角的影响。为了更为准确地得到稳定性的不同，文中对多分支水平井的建模均采用同样长度、同样井径的的主井和支井，建立同样大小的岩体环境，以提高精确度。文中分别对30°、60°、90°、120°和180°的主支夹角情况进行了讨论，以得到最优解。

不同主井夹角的平行井，其位移极值如图7 所示。

通过图7 我们可以看出位移极值的最小值出现在120°主井夹角处，另外90°和180°夹角的最大位移接近。另外通过对比坍塌指数也可以得到相同的结果，在相同边界条件下，不同主井夹角的坍塌指数如图8 所示。

图7 不同主井夹角的位移极值曲线

图8 不同主井夹角的坍塌指数

坍塌指数是一种基于库伦准则，描述某一位置处坍塌可能性的物理量，越容易坍塌的位置坍塌指数越小。90°主井夹角更容易坍塌，120°和180°的井眼稳定性相对较高。结合位移极值情况，后续进一步讨论90°、120°和180°三种井型。通常来说，沿主井眼与外侧支井处的位移最大，三种井型沿井眼进尺的位移如图9 所示。

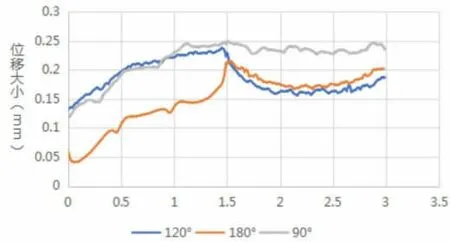
图9 不同主井夹角的位移极值曲线

通过对比三者曲线图我们可以得出，三种井型位移分布差异巨大，对于主井夹角为90 度的井型来说，最大位移大，且均分布在一个较高的范围，所以此种井型不可取。对于120°夹角与180°夹角两种井型来说，通过计算二者位移均值相差不大，且分布也是180°更均匀。但180°主井夹角的井型仍不是最优解。原因有二，一是在井眼进尺相同的情况下，180°主井夹角的井型在煤层中的有效影响范围远小于120°夹角，这会导致后续的开采效率低下；二是在实际工程中，井眼轨迹会是弧线，这会极大增加钻进距离，更大的影响稳定性。因此，选择120°主井夹角的井型综合分析对后续的开发更有利。其井型示意图如图10 所示。

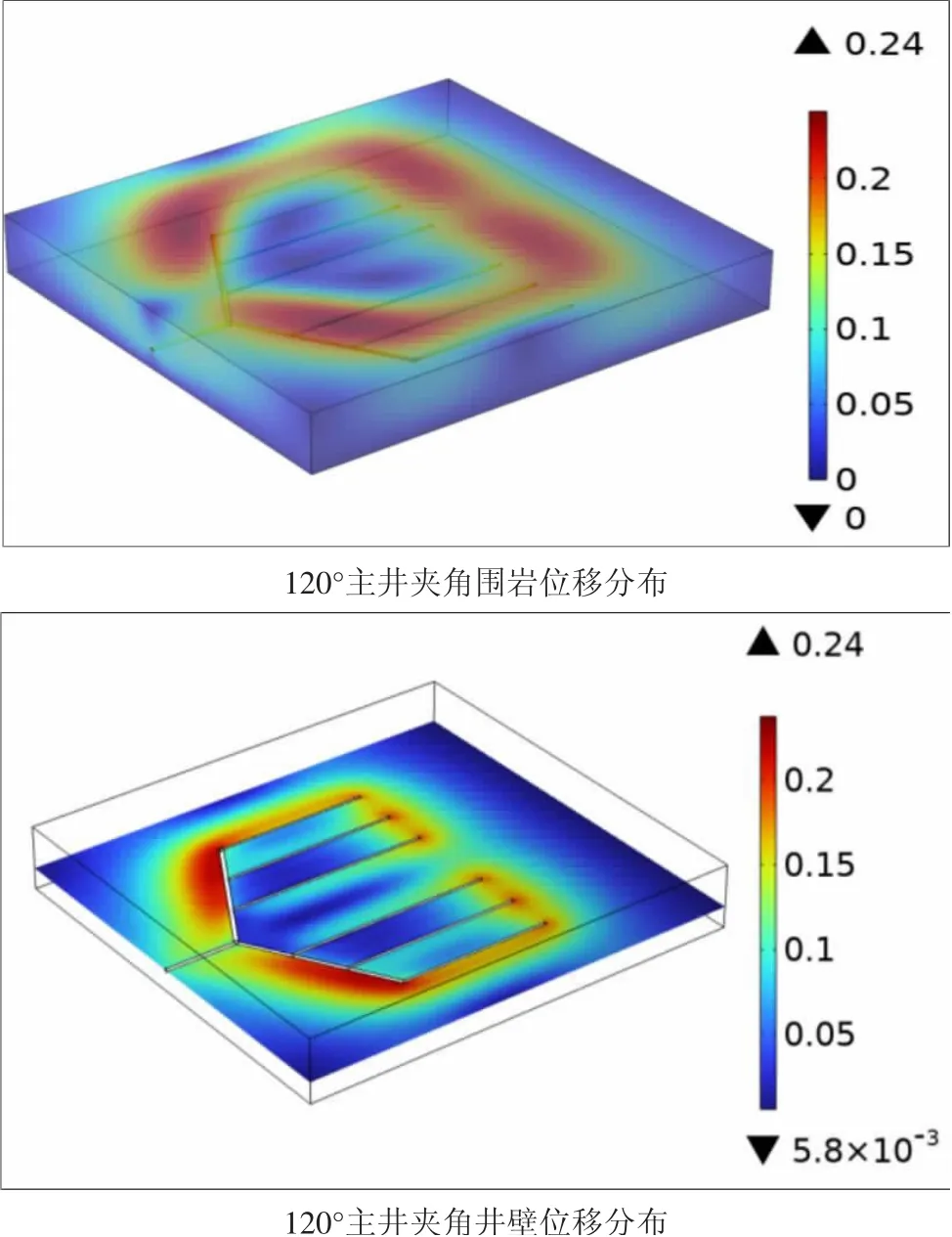
图10 不同主井夹角的位移分布情况

3.3.3 分支井进尺稳定性的影响

在实际钻井完井过程中，井眼进尺通常十分重要。由前文已有结果，我们已经得知，长进尺的支井中部也是应力及位移相对集中的位置。

由于数值模拟将模型简化后，无法对支井进尺进行定量计算。为了使模拟更具有可信度，本文以主井进尺与支井进尺的比作为自变量，即a 与b 的比值。前文所有双主支多分支平行井的主支与分支的比为1:1。（图11 所示）。

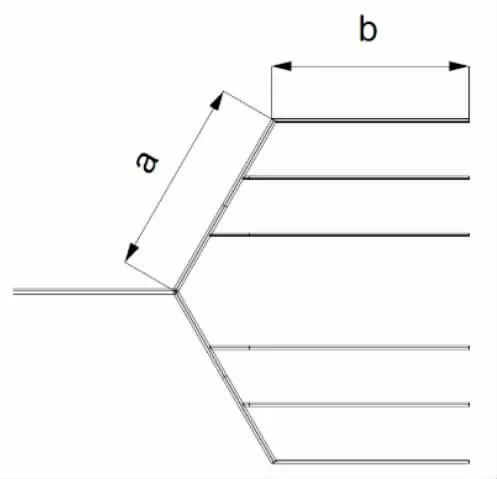
图11 不同主支进尺比示意图

从前文已得数据，本小节只对120°夹角的井型进行自变量讨论。分别讨论主支井进尺比为2:1、1.5：1、1：1.5、1:2 的四种情况，然后得到相对最优解。

通过分析可以得到，不同井型的井筒处最大位移如表2 所示。

表2 不同井型井筒处最大位移

综合分析不同井型的最大位移情况我们可以发现，当主井与支井进尺为1:1.5 之时，最大位移最小，井壁稳定性最高。对比之下，当主井与支井进尺只比为2:1 和1.5:1 之时，最大位移也在合理的范围内。但后两种选择将使水平井控制范围缩小严重。综上所述，只有当主分支进尺在1:1.5 附近时，能使效益最大化。

4 结论

针对里必区块内的多分支水平井井壁失稳问题，采用COMSOL Multiphysics 进行流固耦合分析得到了以下结果：①与现有的单主支多分支水平井相比，采用双主支多分支平行井更有优势。②与羽状井相比，选择多分支平行井更有利稳定性。③多分支平行井采用120°主井夹角综合看来更有利于稳定和排采需要。④位移和应力的极大值处多集中在主井支井夹壁出、井眼端部和长直段中部，在实际排采中应注意这些区域的支撑。