结合高斯投影和抵偿高程面建立GPS 控制网

黄俊伟，陈海春，白世晗*，冯 超，李 霞

（1. 云南省水利水电勘测设计研究院，云南 昆明 650021）

随着我国基建工程的飞速发展，近年来，公路、铁路、电路、城市交通、水利等多行业长距离建设项目日益增多，而长线路GPS控制网是工程大比例尺地形图测量、征地、施工放样的基础[1-2]。如何建立一套科学的建网方案，既满足该控制网与国家坐标系统的联系，又将边长的投影变形控制在允许范围内，是长线路建设工程首先要解决的问题[3-5]。为满足控制网实测坐标反算后，得到的边长和实地量测的边长在长度上尽可能相等，使布设的建筑物位置和施工实施阶段放样位置误差最小，需考虑归算实测边长到椭球面的变形ΔS1与归算至高斯投影面上的椭球面边长变形ΔS2之和ΔS达到最优，以满足施工放样精度[6-9]。

针对上述问题，大量研究人员对长线路GPS控制网的布设做了相关的研究，归纳后大概有如下一些方式：①使用边长尺度约束法对GPS控制网边长进行平差约束。②选择一个适合本工程的中央子午线进行高斯投影。③选择合适的更加符合工程的高程投影面，进行抵偿高程投影改正。本文中某长距离引水工程位于高原山区，跨度数百公里，且地形起伏较大，为建立满足长度变形限差的GPS 控制网，综合使用高斯投影和抵偿高程面的方式，让工程整体精度得到保证。

1 减弱边长变形的方法

1.1 边长尺度约束法

对GPS控制网内点间长度用改化过的边长进行约束平差，间接实现了高斯平面边长归化。一般选择测区中间位置的3 个互相通视的GPS 点，以一个为基点，相连的一条基线为方位角，利用高精度全站仪实际测量该边长控制点间的距离，并用该边长进行约束平差[10-11]。此方法获得的工程坐标系统与国家标准坐标系在局部范围相差不大，但参考椭球的参数却不确定，需要进行校正。该方法一般适用于测区范围较小、不用和其他线路工程进行联系的独立坐标系统[12]。

1.2 高斯投影

该方法还是选择参考椭球面作为实测地面数据的归化面，但高斯投影的中央子午线不再是标准划分的3°带，而是重新选择合适的中央子午线（面积小的工程一般可采用测区中间位置）做投影，使长度投影至该投影带上变形比国家标准3°带投影小。该方法处理原理简单，处理效果相对比较好，不需要重新计算椭球参数，但经过换带投影计算之后，同一地面位置的高斯平面坐标值会产生较大的变化，和国家坐标系数值匹配度不高[13]，如图1所示。

图1 线路每1 000 m长度变形与Ym 之间的关系图

椭球面上任意边长投影至高斯平面会产生长度变形，变形量如式（1）所示：

式中，R为该测区中点的平均曲率半径；S0为边长归算到椭球面上的长度；YM根据测区情况不同会有2种取值方式。

当测区位于中央子午线的一侧时:

当测区位于中央子午线两端时:

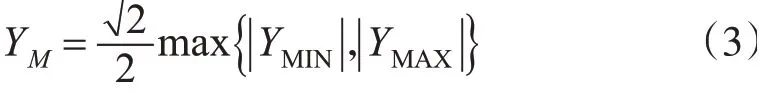
1.3 抵偿高程面法

抵偿高程面法即不以标准参考椭球面实现高斯投影，而是选定更加合适的符合工程的高程面。如图2所示。

图2 线路每1 000 m长度变形与Hm 之间的关系图

该方法产生的变形如式（4）所示：

式中，ΔS2为实地测量边长换算到椭球面上的投影变形；HM为所在高程面相对于椭球面的平均高程；R为该长度所在方向的椭球曲率半径；SA为实地测量的水平距离。

2 综合投影

2.1 使用1°分带进行高斯投影

为减小边缘地区高斯投影变形，对于长线路工程，采取1°分带来代替常规3°分带，经计算可知在1°带区域内，区域边缘位置距离中央子午线的距离约为50 km，区域边缘高斯改化值约为3.2 cm/km。1°分带减小了测区边缘的高斯改化的最大变形，但受高原山地海拔较高影响，某些区域测距边投影到参考椭球面的高程改化变形值还是很大。故在地形起伏较大的地区除了进行1°分带，还需设置抵偿投影面来控制高程归化变形。

2.2 建立合适的抵偿高程面

要实现控制变形，依据上文分析，则需考虑控制YM处变形最小，虽然实际地形并非平均高程面，难免存在高低起伏，但一定高差内变形可被控制。可以取H0为抵偿高程面，当确定测区YM值之后，即可计算平均高程面Hm与抵偿高程面H0之间的高差ΔH，如图3所示。

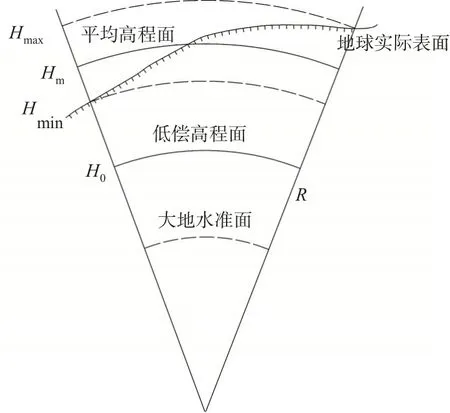
图3 平均高程面与抵偿高程面示意图

如上图所示:

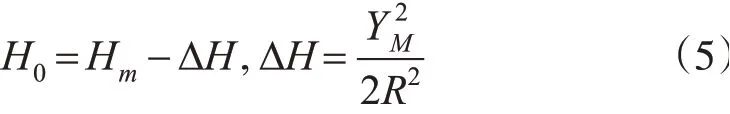
式中，YM的计算由上文分析所得，当测区位于中央子午线的一侧时，当测区位于中央子午线两端时，

2.3 高斯投影

综合高斯投影和高程抵偿面投影，边长变形ΔS=ΔS1+ΔS2，长度综合变形公式为：

由上式可以看出，当采取综合考虑选择合适的中央子午线和抵偿高程面时，可使得测区长度综合变形最小。故可采用二者结合的方式，应用于长线路引水工程，进行工程GPS控制网的建立。

3 案例分析

以云南某大型引水项目为例，工程以输水线路为主，线路总长约700 km。项目东西跨度超过230 km，经度范围约在100°31′～102°55′E 之间，测区高程起伏变化从1 200～1 980 m，平均海拔1 600 m。

3.1 投影面的确立

1）将线路区域按覆盖的经度，按1°带分带，将整数1°的子午线作为中央子午线，即101°、102°、103°为中央子午线。

2）为了控制工程的变形量，还需将观测边长投影至合适的高程面上。高程面的按2.2、2.3 节方法计算后选取1 780 m、1 650 m、1 510 m、1 300 m 共4 个投影高程面，整体设计保证每个投影面上至少有3 个一等点，利用一等平面控制点的施工测量坐标系成果为起算数据，计算二等平面网的施工测量坐标系成果。为方便项目设计施工衔接，两两投影面相交区域需提供两套成果便于转换。

3）测区投影面划分：①101°中央子午线下1 780 m投影面；②101°中央子午线下1 650 m投影面；③102°中央子午线下1 650 m 投影面；④102°中央子午线下1 510 m 投影面；⑤102°中央子午线下1 300 m 投影面；⑥103°中央子午线下1 300 m投影面。

3.2 控制网布设

1）为满足测绘规范要求，针对该项目实际情况，对项目进行两级控制网布设。一等平面控制网（本工程平面一等网精度要求参照GPS B级网执行）作为整体项目的框架基础，平均间距约40 km 一个点进行布设，将整个工程连成一个整体，工程共计布设一等点26 个。为保证工程和国家坐标系衔接，工程布设平面一等网就近联测国家控制点，共联测了8 个国家平面已知点（其中包含国家一等点4个、二等点1个、B 级点3 个）。控制网观测实施按GB/T 18314-2009《全球定位系统（GPS）测量规范》中的B 级网要求执行。

2）二等网点是工程建筑的首级施工控制网（本工程平面二等网精度要求参照GPS C级网执行），主要考虑布设在工程建筑物附近便于施工放样，一般每个建筑物附近至少有4 个两两互相通视的控制点，工程共计布设二等点284 个。与一等控制网联合观测解算，施测时候所有一等网都放进二等网里进行观测。控制网观测实施按GB/T 18314-2009《全球定位系统（GPS）测量规范》中的C级网要求执行。

3）控制网解算方法及投影：①一等网整体平差得到一等网国家2000坐标系；②一等网根据划分的投影区域进行椭球膨胀把控制网投影到相应高程面上，中央子午线采用坐标转换法把3°带成果转换为1°带成果。得到相应的工程坐标系；③各投影区域分别进行平差计算，以区域内一等点为已知点，进行二等网平差计算，得出二等网的工程坐标系，相邻区域的地方二等网需解算2 个区域的成果，以便后期不同施工区域的衔接。

3.3 几种投影方式精度分析

为比较不同投影方式下该项目边长变形，现以项目最东一个测区（101°中央子午线下1 780 m 投影面）进行讨论。以下是该区域内部分二等网边长在不同投影方式下和全站仪实测边长的对比：

1）按照标准3°分带，测区平均高程面进行投影变换。测区若采用国家3°带坐标系，则中央子午线为102°，使用该段平均高程面1 810 m 作为投影面，全站仪实测边长和投影坐标反算距离比较分析如表3。

表3 实测边长比较表

2）按照1°分带，测区平均高程面进行投影变换。1°分带下测区中央子午线为101°，使用平均高程面1 810 m 作为投影面，全站仪实测边长和投影坐标反算距离比较分析如表4。

表4 实测边长比较表

3）按照1°分带，测区抵偿高程面进行投影变换。1°分带下测区中央子午线为101°，选择抵偿高程面为投影面。依据前文推导，计算得YM= 44 km，H0=1 780 m，17 80 m 即作为高程投影面。用全站仪实测边长和投影坐标反算距离比较分析如表5、图4所示。

图4 不同投影方式引起的变形差异

表5 实测边长比较表

分析不同投影方法下变形差值可得出：针对长线路大高差工程项目，常规的标准3°分带边缘区域距离中央经线距离较远，约140 km，引起变形较大，超过10 cm/km，不能满足行业规范和设计施工需求；对该项目进行1°分带建立独立的施工测量坐标系，大幅度减少了测区距离中央经线的距离，有效降低了长度变形。但若不考虑合适的投影高程面，仅简单使用测区平均高程，部分区域长度变形仍存在超过2.5 cm/km情况，未满足规范要求；对该项目采用1°分带，并计算抵偿高程面，科学合理的选择投影高程面，可有效降低长度变形，使得测区整体变形得到控制，满足规范精度要求。

4 结 语

本文针对高原山区长线路GPS控制网长度变形超限的困扰，分析了减弱边长变形的不同方法，研究了投影变换方式的确立，提出了科学合理、满足规范要求的建网思路。通过理论推导，发现地形起伏较大的山区高斯投影和高程归化改正变形值存在正负抵消减弱的情况，并依据实际案例，运用1°分带高斯投影和抵偿高程面的方式，进行长线路GPS 控制网的建立。通过理论分析和案例计算，验证了该方法能有效降低投影变形，误差满足规范精度要求，满足高原山地施工控制网建网要求。