Kerr-Newman 黑洞周围的精确光子轨道
李大刚,冯启敏
西华师范大学
2019 年,LIGO 事件视界望远镜为我们提供了一个超大质量黑洞周围的光学图样[1-2],这是人类首次直接观察到黑洞的样貌。据此我们可以看到黑洞周围有一个明亮的光环,中间的黑色区域就称为黑洞的阴影。这是一个由质量M 和角动量J 的真空爱因斯坦场方程的Kerr 解所描述的黑洞,没有其他参数(如电荷参数)。对于光子运动的研究可以帮助我们探索时空的几何性质。不稳定的光子轨道定义了黑洞捕获和非捕获之间的边界,对这些轨道的研究,也可以帮助我们更好地研究黑洞阴影[3-4]。但由于时空对称性所导致的数学上的困难,对于大多数的光子轨道研究都只能得到数值解。另一方面,对于稳定的光子轨道的研究也可以帮助我们分析吸积盘的光学外观[5]。对于黑洞阴影近年来有很多的观测与理论研究。黑洞的发现在某种程度上说明了广义相对论这一引力理论的正确性,但为进一步验证广义相对论这一引力理论的正确性以及进一步探索在更具一般性时空的几何性质,我们有必要研究带电轴对称黑洞周围的光子轨道,特别是在弯曲时空中光子轨道与黑洞参数之间的精确关系[6]。Aydin Tavlayan 和 Bayram Tekin 以Kerr 黑洞为研究对象,借助Fintan D. Ryan 所提出的有效倾角的定义再结合径向方程得到了光子轨道半径与黑洞转动参数之间所满足的关系,这是一个一元六次方程。若能求解这一方程就可以得到光子轨道半径与转动参数之间的精确关系。但由于高于四阶的一元方程不存在根式解,因此对于这一六阶方程的求解就需要一些巧妙的方法。在本文中,借助Aydin Tavlayan 和Bayram Tekin 的这一方法,我们分析了Kerr-Newman黑洞周围的光子轨道与黑洞参数之间的精确关系。我们发现,对于Kerr-Newman 黑洞,光子轨道半径与黑洞的转动参数以及电荷参数之间同样满足一个一元六次方程,这个一元六次方程可以被分解为一个一元四次方程与一个一元二次方程乘积的形式,二次方程部分给出视界内部光子轨道半径与转动参数以及电荷参数之间的关系,四次方程部分有两个实根以及两个没有物理意义的复根。众所周知,在轴对称黑洞外部有两个光子轨道,一个轨道的光子运动方向与黑洞转动方向同向,称其为顺行轨道,而另一个轨道的光子运动方向与黑洞转动方向反向,称其为逆行轨道[7]。存在两个光子轨道以及光子运动方向的原因Edward Teo在文献[8]中有比较详细的描述。而四次方程的两个实根恰好分别表示顺行轨道以及逆行轨道的半径与转动参数以及电荷参数之间的关系。这一方法同样可以推广到Kerr-Newman-Kasuya 黑洞和Kerr-Sen 黑洞。随后,我们描绘出了光子轨道半径与转动参数以及电荷参数之间的关系图像。最后,我们分析了光子轨道的稳定性问题,并做了简要总结与讨论。
1 Kerr-Newman 黑洞周围的精确球形光子轨道及其稳定性
在标准的 Boyer-Lindquist 坐标系下,Kerr-Newman 时空的线元可以表示为:
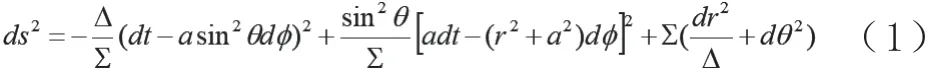
其中,

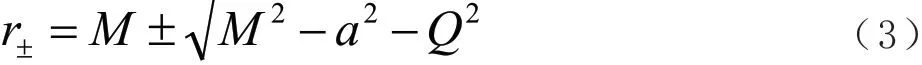
为了得到光子在Kerr-Newman 黑洞周围的运动方程,对哈密顿雅可比方程分离变量后可得:

其中,
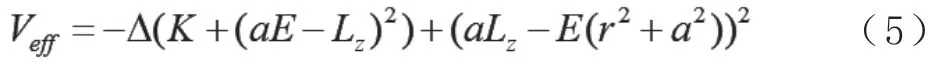
这里E 表示光子的能量,λ表示仿射参量,Lz表示光子角动量的z 分量,K 表示卡特常数。在后文中,我们令我们分别称u、q为转动参数与电荷参数。对于圆形的光子轨道需要满足条件由此可得以下两组解:

但是文献[8]告诉我们当卡特常数小于零时是非物理的,因此我们只讨论第二组解并借助有效倾角的定义

令v= sin2i,则可得到如下的一元六次方程:
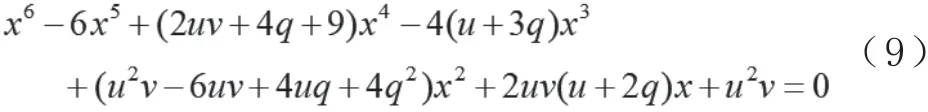
仅当q=0 时,这便回到了Kerr 时空下光子轨道半径与转动参数所满足的关系,由于转动参数u的存在,这依然是一个一元六次方程;仅当u=0 时,便得到了Reissner-Nordstrom 时空下光子轨道半径与转动参数所满足的关系,此时是一个一元四次方程,如下:
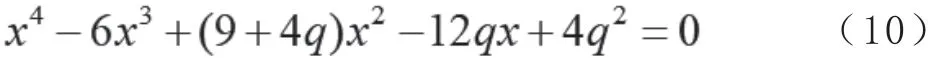
可以解得:

当u=0 且q=0,得到Schwarzschild 时空下光子轨道半径与黑洞质量所满足的一元二次方程,且是一个完全平方的形式:

其结果为我们熟知的x=3,或r=3M,即在Schwarzschild 黑洞周围可以存在一个r=3m 的圆形光子轨道。将(13)式分解为如下的形式:
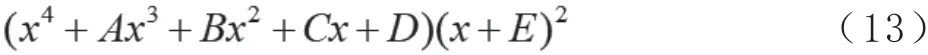
A、B、C、D、E表示待定系数,我们发现此时
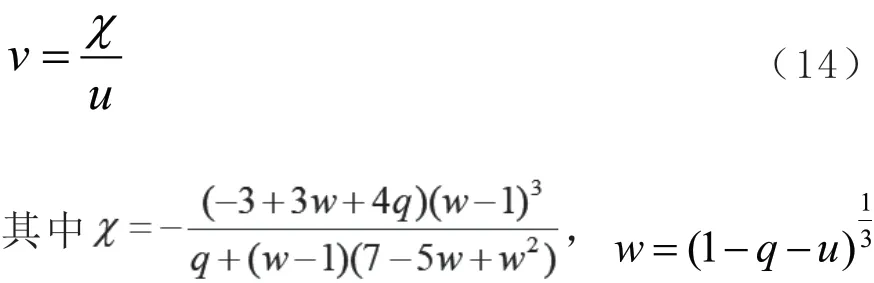
由于v= sin2i,因此0<v<1;对于v<1不难证明是恒成立的,不过要使得0<v,u要满足如下范围:

对于非极端黑洞情况,还要满足u<1-q。另外对于电荷参数q所满足的范围,当转动参数u介于0到0.5 或者介于0.5 到1 时,电荷参数q 满足不同的范围,下面以u等于0.25、0.5 和0.75 为例,画出v随电荷参数q的图像。

图1 Kerr-Newman黑洞参数v当转动参数取不同值时与电荷参数之间的关系图
当0 <u<0.5, 要 满 足0 <v, 则0 <q当0.5 <u<1,要满足0 <v,则0 <q<1-u。由于方程(14)及其解太复杂,在本文中仅给出方程(14)各待定系数与转动参数以及电荷参数之间的关系。

由此可以通过求解方程(14)得到Kerr-Newman黑洞周围光子轨道半径与其转动参数以及电荷参数之间的关系,下面给出当电荷参数取某些特定值时光子轨道半径与转动参数的图像。

图2 Kerr-Newman 黑洞周围光子轨道半径在不同电荷参数时与转动参数之间的关系
三条曲线从上到下分别表示逆行、顺行和视界内部的光子轨道,上面几幅图分别表示电荷参数取0、0.125、0.25、0.5、0.67,相应的转动参数范围为[0,1],[8/27,7/8],[49/108,3/4],[25/54,1/2],[242/729,1/3]。当q=0,则回到了Kerr 黑洞的情况。
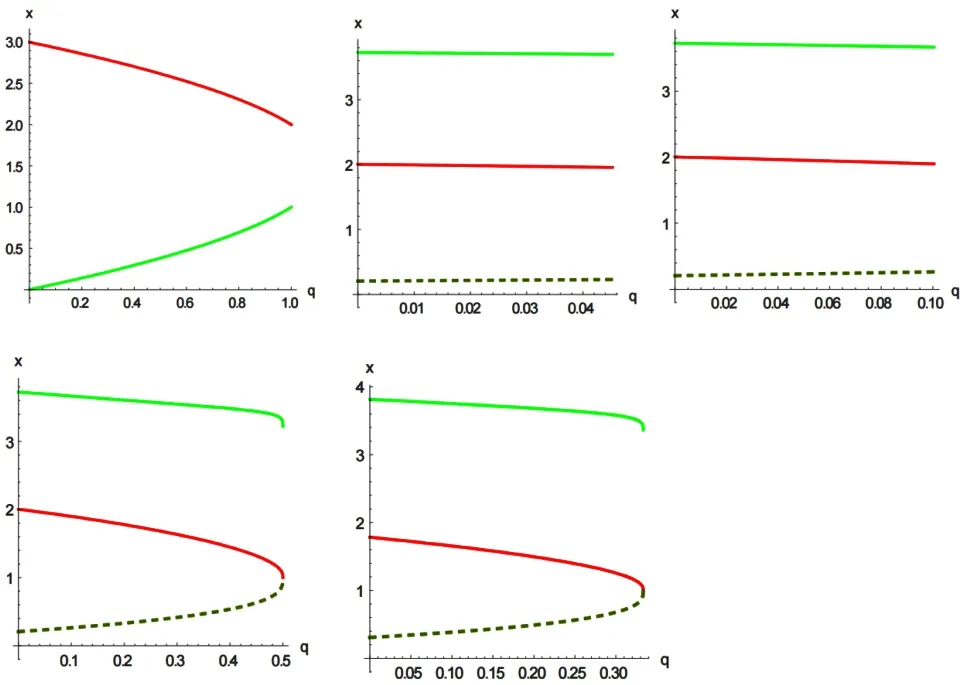
图3 Kerr-Newman 黑洞周围光子轨道半径在不同转动参数时与电荷参数之间的关系
三条曲线从上到下依然分别表示逆行、顺行和视界内部的光子轨道,上面几幅图分别表示转动参数取0、0.125、0.25、0.5、0.67 时,相应的电荷参数范围 为[0,1],[0,0.0452],[0,0.1005],[0,0.5],[0,0.33]。当u=0,则回到了Reissner-Nordstrom黑洞的情况。

2 结论
带电轴对称黑洞附近的光子运动对于天体物理学很重要,为了研究更具一般性时空的几何结构,本文基于爱因斯坦的广义相对论以及麦克斯韦理论得到的Kerr-Newman 黑洞,定量研究了该时空下光子轨道半径与黑洞的电荷参数和转动参数之间的关系以及轨道的稳定性问题,因为它所描述的时空比Kerr 时空更具一般性。到目前为止,我们已经知道Kerr 黑洞周围的
[1] 吴学兵.史上首张黑洞照片的科学与技术[J].科学通报,2019,64(20):2082-2086.
[2] 袁业飞,唐泽源.事件视界望远镜对近邻星系M87 中心超大质量黑洞的成像观测[J].科学通报,2019,64(20):2072-2076.
[3] 赵凡,贺锋,任文辉.遥远星体在太阳引力作用下形成的爱因斯坦环[J].大学物理,2018,37(5):49-51.
[4] 陈远.Quintessence包围的旋转Hayward-de Sitter黑洞的黑洞阴影[D].兰州:兰州大学,2021.
[5] 刘雄辉.弯曲时空中的粒子轨迹[D].武汉:武汉大学,2018.
[6] 马宸.Ca(?)ate-Bergliaffa黑洞最大延拓时空的时空结构与其光子球及类时稳定圆轨道研究[D].昆明:昆明理工大学,2021.
[7] 赵凡,贺锋.Kerr 时空赤道面上零测地线方程的严格求解[J]. 大学物理,2018,37(7):23-24,46.
[8] E.Teo,Spherical orbits around a Kerr black hole, Gen. Rel. Grav.53, no.1,10 (2021).

