多因素耦合作用下缓冲材料对铀的长期阻滞效应数值模拟
王 哲,王玉平,李江波,张振龙,冯喜杨,罗 莹,张家千,曾秋平,刘 艳,易发成,张 灏,赵 雨,王振雨,吴亚东
1.西南科技大学 核废物与环境安全国防重点学科实验室,四川 绵阳 621010;2.中国科学技术大学 地球与空间科学学院,安徽 合肥 230026;3.宜宾学院 国际应用技术学部,四川 宜宾 644000;4.中国工程物理研究院 材料研究所,四川 江油 621700;5.四川轻化工大学 计算机科学与技术学院,四川 宜宾 644000
随着核技术的广泛应用,不可避免地产生大量的放射性废物,特别是那些具有放射性强、毒性大、半衰期长、释热率高和处理难度大的高放废物,需要对这些放射性废物进行有效地安全处置,才能够避免其进入生物圈而对环境和人类健康构成严重威胁。目前,对于高放废物的安全处置,国际上普遍接受的、唯一可行的处置方式是深地质处置[1-5](图1[5])。 它是一项以核素的固化、阻滞为核心内容,以多重屏障为主要手段,以1万年~10万年时间尺度内人类健康和环境不受其破坏为目标的处置库系统工程[6]。高放废物深地质处置库的长期稳定性取决于多重屏障体系中各子系统的长期安全性,即天然屏障的完整性及工程屏障的长期有效性,而前者与场址的地层岩性、地质构造与岩体的力学稳定性及地下水赋存情况有关,可通过选取有利工程地质与水文地质条件及完整性好的围岩来实现,后者可通过优化处置单元设计和选取性能优良的工程屏障材料(选取有利的固化体、废物罐与缓冲材料)来实现[7-8]。
在高放废物深地质处置的多重屏障系统中,缓冲材料可作为最后一道人工屏障,对放射性核素的吸附滞留及阻滞特性将直接影响到放射性废物随地下水逐渐渗出地质屏障而返回到生物圈的能力。因此,从这个意义上说,研究放射性核素在缓冲材料中的吸附、阻滞特性对高放废物深地质处置库的长期安全性具有重要的意义。放射性核素迁移并返回生物圈的主要动力是作为核素传递载体的地下水的流动和核素浓度差引起的扩散,而阻滞核素迁移的因素主要是天然及人工工程屏障对放射性核素的吸附作用。因此,核素阻滞效应研究的内容就是放射性核素在天然地质体和各种人工屏障材料中的吸附、滞留、扩散以及在地下水中的迁移行为特征[9]。

(a)——竖向处置单元, (b)——水平处置单元图1 高放废物深地质处置库示意图[5]Fig.1 Schematic diagram of high-level radioactive waste deep geological disposal repository[5]
目前国内外关于放射性核素迁移的研究主要是通过室内模拟实验来测定各种放射性核素在多种屏障材料中的吸附分配系数Kd、阻滞因子Rd、扩散系数D和容量因子α,来表征放射性核素在屏障材料中的吸附、滞留、扩散性质以及在地下水中的迁移行为、迁移规律和迁移模型[10-12]。
20世纪70 年代,美国、瑞典、英国等国在这方面作了大量的工作,其中具有代表的是英国的Bradbury 等[13]的研究,他们研究了86Sr、99Tc、137Cs等核素在花岗岩、砂岩等介质中的吸附及一维扩散行为,证明了核素在岩石中的扩散也符合Fick 扩散定理,并由实验曲线获得了核素扩散系数、岩石容量因子和吸附系数等参数。进入20世纪 80 年代后,我国也开展了核素迁移方面的相关研究工作,对Sr、Cs、I、Co、Ru、Ce等元素在花岗岩、灰岩、泥土与地下水等介质中的迁移进行了较多的研究,测得一系列渗透、扩散和滞留参数,并利用这些参数作出了放射性核素的浓度随迁移距离和迁移时间的变化关系图[14]。
当多重屏障体系的高放废物深地质处置库在关闭并投入运营后,在一定的时期内,地下水通过浸润将使缓冲层逐渐饱和并与包装容器直接接触。随着时间推移,废物包装容器在辐照、地下水腐蚀及应力等作用下,最终包装容器锈蚀和破裂,核素将随着地下水的渗流在整个多重屏障系统内进行迁移,其迁移过程主要有三个阶段:第一阶段为核素释放-扩散迁移,即核素在工程屏障中的迁移;第二阶段为核素在天然地质屏障中的对流-弥散迁移;第三阶段为核素在生物圈中的分区传递[15-16]。而缓冲材料对核素的阻滞效应,将直接影响到核素在第二、第三阶段中的迁移进程及处置库系统的长期稳定性与安全性。
由于放射性衰变,核废物随着时间不断放热(几千年~一万年),并在人工屏障中传输,改变了缓冲材料的温度,进而引发缓冲材料体积膨胀和热应力,改变流体的性状和运动,破坏水-缓冲材料间的化学平衡并产生新的地球化学作用;而地球化学场具有特别重要的作用,表现在因温度、湿度变化导致处置库近场的化学作用引发的化学成分变化对固化体的溶解与核素的析出具有重要作用,进而对核素在缓冲材料中的对流、扩散及吸附等物理化学过程产生影响[17]。可见,在处置库的近场环境条件下,核素在缓冲材料中迁移扩散受控于温度场(T)、渗流场(H)、膨胀应力场(M)和化学吸附场(C)的耦合作用,并且这种复杂的THMC耦合作用会直接影响到以核素为核心的溶质迁移。为了揭示处置库环境中多场耦合作用下缓冲材料行为变化的规律,瑞典、加拿大、比利时、日本、捷克、西班牙、法国、韩国等国研究人员开始对本国高放废物处置库预选膨润土进行了多场耦合条件下的长期性能实验[18-27]。此外,为了对高放废物处置库长期稳定性进行评价,国际上已经开展了数项重大合作项目,先后开展了DECOVALEX项目、FEBEX项目和China Mock-up项目等,为推动高放废物地质处置安全评价作出了重要贡献[28-33]。要充分理解这些耦合过程,数值建模是一个不可或缺的工具,因为处置库的安全性必须保证10万年或更长时间。然而,在缓冲材料中模拟THMC耦合过程是具有挑战性的,一方面因为耦合过程的本构关系复杂且难以获得,另一方面本构关系的选择和参数对模拟结果有很大影响。THMC多场耦合研究的数值软件主要有TOUGHREACT、FLAC3D和COMSOL。Nardi等[34]采用Java开发了一款能够有效协同多物理场耦合分析软件COMSOL Multiphysics与地球化学模拟软件PHREEQC的接口(iCP),可以有效地处理复杂的地球化学反应过程与其他物理过程的耦合,为有效模拟大量与地球化学反应过程有关的多物理耦合问题提供了一个数值模拟平台。Nasir等[35]基于COMSOL Multiphysics有限元和PHREEQC,并利用MATLAB编写一个连接两个软件的代码,开发了一种新的模拟工具,实现了两种软件的耦合,完成了模拟核废料深部地质库(DGRs)近场发生的热-水-力-地球化学(THM-GeoC)耦合过程及其对岩石孔隙度和渗透率演化的影响。张志红等[36]基于流体的守恒方程,建立了某一个溶质在饱和的土体中迁移的THMC全耦合模型,并使用COMSOL软件研究了渗滤液在不同环境温度下对溶质迁移的影响。郭志光等[37]建立了非均衡吸附问题理论模型并利用COMSOL数值分析方法讨论污染物迁移规律。张玉军[38-40]将渗透迁移行为引入THM耦合控制方程中,建立了THMC耦合模型,将其运用到假想的核素泄漏后的地下处置库中,并对产生泄露的处置库进行多场耦合数值计算,研究其温度、核素浓度、正应力随时间的变化和分布情况。林文胜等[41]分析了世界各国对高放废物处置设施THMC耦合效应的研究进展。刘泽佳等[42]在温度影响的前提下,将化学函数添加到孔隙水中,用来模拟有机污染物对多孔介质力学性质产生的影响,建立了一个关于多孔介质的THMC数学模型。Yasuhara等[43]建立了一种THMC耦合数值模型,通过模拟高放废物深埋地下情景,应用模拟围压和温度条件,预测岩石渗透性的长期演化,模型预测清楚地显示出压力溶解对渗透率随时间变化的显著影响。Changsoo等[44]为了提高韩国高放废物的处置密度,提出了一种多层储存库的概念来替代单层储存库的概念,采用数值模拟的方法比较了现有韩国高放废物处置库的THMC耦合行为。Cinzia等[45]利用地下水模拟程序PMWIN,以非均匀地下水流场为例,模拟了放射性核素在地质处置库的远场迁移过程并讨论了分布系数及水力梯度两个重要参数对地下水流场的影响。上述关于高放废物地质处置库的长期稳定性评价工作主要侧重于天然地质体和开挖扰动区内裂隙岩体的多场耦合研究,较多且较全面,其研究主要集中在热-水-力等多场耦合作用下对岩体的物理力学性能响应特征及数值模拟。而关于缓冲材料在多场耦合作用下的性能研究,主要关注于压实膨润土基缓冲材料在多场耦合条件下的物理力学特征的变化规律,并未对多场耦合作用下核素在缓冲材料中的迁移扩散行为进行深入研究。因此,本工作拟通过建立饱和缓冲材料温度场、渗流场、膨胀应力场和化学吸附场的耦合数学模型,基于模型实验获得的参数,采用多物理场仿真软件COMSOL中的PDE接口和内置接口,将推导出的控制方程和本构关系进行导入,建立多因素耦合作用下缓冲材料对核素的长期阻滞效应的数值模拟方法,为工程实践和放射性废物的安全处置提供有价值的依据,同时也能够为我国高效废物深地质处置库地下实验室开展1∶1工程尺度的工程屏障设计与安全性能评价提供具有参考价值的科学数据。
1 饱和缓冲材料中核素迁移扩散的热-水-力-化耦合模型建立
1.1 模型假设
为构建建立在弹性力学基础上的多孔介质热-水-力-化耦合数学模型,需作出如下假设[9]:
(1) 非饱和的介质被视为多相系统(固体、液体和气体);固体骨架的孔隙部分被液态水填充,部分被气体填充;气相假定为由干燥空气和水蒸气组成的理想气体混合物;液相假定为水和溶解的空气组成;
(2) 多相介质被认为是一种混合物;每一相都是连续的,混合物中的每一个空间点都被认为同时被每一相的一个物质点占据;混合物作为一个整体的平衡定律与单相物质平衡定律的方程形式相同;
(3) 气相密度是温度和压力的函数,且满足理想气体状态方程;
(4) 流体渗流运动满足广义的Darcy 定律;气相气体中包括水蒸气和干空气,两者压力分布符合 Dalton 分压定律,饱和蒸气压力满足 Kelvin 适度定律;水蒸气的扩散符合广义 Fick 定律;
(5) 多孔介质的变形满足小变形假设,且假定无论饱和、还是非饱和状态下,修正的Terzaghi有效应力原理均能适用;
(6) 热传导过程满足广义Fourier定律,并且假定固相、液相、气相,三相保持局部热平衡状态,即在空间内的任意一点,固相、液相、气相,三相均具有相同的温度,并且两相之间的热交换只存在于相变过程中;
(7) 缓冲材料对放射性核素的吸附过程是线性的、可逆的等温吸附;
(8) 放射性核素迁移到缓冲材料之前就已达到水饱和状态,且固体骨架不发生变化;
(9) 放射性核素在缓冲材料迁移的过程中不考虑由于化学反应而引起核素质量的变化,遵循质量守恒;
(10) 除了从高放废物固化体中浸出的放射性核素外,不存在其他源项,核素在固相和液相中浓度达到平衡;
(11) 不考虑放射性核素衰变对源项浓度的影响。
1.2 饱和缓冲材料中核素迁移扩散的热-水-力-化耦合控制方程
耦合过程的分析不是单独的,物理场变量与其它物理场变量之间相互影响[46]。多孔介质的多场耦合研究了温度场、应力场、渗流场和化学场耦合作用下单相流或两相流体在孔隙中的传输,以及固相骨架和流体温度的分布和固相骨架形变的规律。因此,高放废物处置库中的缓冲材料作为一种多孔介质,满足多场耦合作用的理论体系,其中就包括:连续介质理论、混合物理论、渗流力学、传热学理论、普遍的守恒原理及污染物扩散Fick定律等。
为了建立核素在缓冲材料这种多孔介质中迁移扩散的多场耦合数学模型,需要结合混合物理论和连续介质理论以及三大守恒定理(质量守恒、动量守恒、能量守恒)与溶质扩散的Fick定律来推导饱和缓冲材料中核素迁移扩散的热-水-力-化耦合控制方程。
(1) 饱和缓冲材料动量守恒方程
当没有惯性力的情况下,非饱和缓冲材料动量守恒方程为式(1)。

(1)
式中:α代表不同的相,即s表示固相、l表示液相和g表示气相;ρα,α相的本征密度;nα,α相占据的体积比例;vα,α相(组分)的绝对速率;ρα,α相的表观密度;bα,单位质量α相(组分)的体积力大小;σs,固相应力张量;σl,液相应力张量;σg,气相应力张量。
采用小变形假设和小速度假设,即vα≈0,整个过程看作准静态过程,式(1)可简化为式(2)。
契约是指“依照法律订立的正式的证明、出卖、抵押、租赁等关系的文书”。1932年美国律师学会在《合同法重述》中所下的定义是:契约是“一个诺言或一系列诺言,法律对违反这种诺言给予救济,或者在某种情况下,认为履行这种诺言乃是一种义务”。市场经济其实就是契约经济。国有企业以及国有控股的混合所有制企业,有时会依赖自己占有的公共资源和垄断地位对外漠视规则和契约精神,这种作风延伸到自身的企业治理上由于不重视契约的管理带来的管理漏洞也是比比皆是。很好地把契约化管理的思想应用到企业管理过程中,一方面契约签订的过程可以促使科学决策,另一方面所有的经济业务行为的决策都有轨迹可跟踪,利于监督追责。
(2)
而对于饱和多孔介质,不考虑气相,式(2)可以写为式(3)。
(3)
根据有效应力原理,饱和多孔介质的有效应力(σ′)可以表示为式(4)。
σ′=σs+σl=σ-plδ-KβsTTδ-Kζcδ
(4)
联立式(3)与式(4)并写为时间导数的形式,得到饱和缓冲材料动量守恒方程(式(5))。
(5)
式中:c,溶质浓度;ζ,化学膨胀系数;T,温度;σs,固相应力;σl,孔隙水应力;pl,孔隙水压力;βsT,固相体积热膨胀系数;K,土体的排水体积模量;δ,Kronecker Delta单位张量;σ,总应力张量。
引入弹性本构关系与Cauchy几何方程(式(6))。
σ′=D∶ε
(6)

(7)
式中:D,土体的弹性张量;ε,应变张量;u,位移向量。
(2) 饱和缓冲材料质量守恒方程
在饱和状态下,根据理论和实验研究,除水力梯度外,考虑温度梯度和浓度梯度也会改变流体的运动,这种现象称为Soret效应和Dufour效应。因此,考虑Soret效应和Dufour效应的广义达西定律为式(8)。
(8)
同时,在达西定律中,速度其实是指流体相对于固体的速度,即为液体相对于固相骨架的平均流速(vr),计算如式(9)。
(9)
式中:n,饱和多孔介质的孔隙率;vf,饱和状态下流体的实际流速。
依据非饱和缓冲材料质量守恒方程中的水体质量守恒方程(式(10)),因不考虑汽化现象,故去掉源汇项,可得流体的质量守恒方程式(11)。
(10)
(11)

(12)

(13)
将式(9)带入式(11)得式(14)。
(14)
将式(14)展开,可得式(15)。
(15)

(16)

(17)
将式(13)与式(16)相加,并联立式(8)、(9)、(17),可得整体的连续性方程式(18)。
(18)
而在饱和状态下,对于多孔介质密度变化较小的情形,多孔介质密度可以表示为式(19)[48]。
(19)
并且可知式(20)。
(20)
式(19)对时间求导可写为式(21)。
(21)
根据广义Darcy定律,忽略惯性和黏性效应,以及温度梯度对液体流场的热驱动作用,则液相的相对表观速度表示为式(22)。
(22)
由于α=1-K/Ks为Biot系数, 将式(16)、(18)和式(22)带入式(14)可得饱和缓冲材料质量守恒方程式(23)。
(23)
式中:Ks,固体基质的体积模量;βlT,液体的热膨胀系数;ρs0,多孔介质基质初始密度;T0,多孔介质内初始温度;pl,孔隙水压力;clp,水体的压缩性系数;εv,土体的体积应变;σ′,有效应力;σ′0,有效孔隙水应力;μs,固相位移量;εij,应变张量场;ui,i,位移场;δij,Kronecker符号。
(3) 饱和缓冲材料能量守恒方程
将非饱和缓冲材料能量守恒方程式(式(24))中的气相耦合项去除,并将达西定律替换为式(8),可得饱和状态下的缓冲材料能量守恒方程式(25)。
{T[ρs(1-n)cs+ρlnScl+ρgn(1-S)cg]+
(24)
(25)
式中:cl,液相的比热容;cs,固相的比热容;cg,气相的比热容;λ,导热系数;Kl,液相成分体积模量;Kg,气相成分体积模量;kgr,气相的相对渗透率;kgT,混合气体热驱动系数;psv,饱和蒸汽压力;pv,蒸汽压力;ω,为液相迁移系数;μg为气体的动力黏滞系数;βl,液体的线热膨胀系数;βs,固体的线热膨胀系数;βg,气体的线热膨胀系数;Tg,气体温度。
(4) 饱和缓冲材料溶质迁移方程
放射性核素在缓冲材料中的迁移扩散受核素-缓冲材料相互作用与地下水水动力学过程两方面因素共同控制,因此,放射性核素迁移模式是由核素吸附模式和地下水水动力学模式耦合而成的,在建立饱和缓冲材料中核素迁移方程时,需要考虑地下水的溶质对流作用、水动力弥散作用与核素的吸附作用[9,11]。
其中,溶质对流是指当地下水在缓冲材料中渗流时,同时携带着核素离子以水的流动速度在孔隙中迁移。这种随水流运动而携带的溶质的数量,称为溶质对流通量Jv。当渗流为达西流时,随之携带的溶质对流通量与缓冲材料中核素的浓度c成正比[49](式(26))。
Jv=vfc
(26)
当含放射性核素的地下水在缓冲材料中迁移时,由于孔隙存在使各点的流速向量和横断面平均流速向量的方向、大小各不相同,所以通过不同孔隙的核素离子在一定时间间隔所达到的位置也不同,这是由于含有核素的地下水具有黏滞性、孔隙大小不同及分布不均和固体颗粒的阻挡所以引起的。因此,在建立缓冲材料对核素的迁移阻滞模型时需要考虑水动力弥散作用的影响。一般来说,水动力弥散作用主要包括分子扩散和机械弥散作用,它是一种不稳定和不可逆的过程[50]。其中:分子扩散是由于液体中所含核素浓度分布不均时,核素会在浓度梯度作用下从高浓度处向低浓度处迁移,它不受液体流动本身的影响[51]。核素扩散通量可用Fick定律描述,即核素的扩散通量与其浓度梯度成正比,扩散方向与浓度梯度方向相反[52],即Fick第一定律,如式(27)所示。
(27)

机械弥散也称对流扩散,指含核素地下水流体通过缓冲材料中孔隙的平均流速(即渗流速度)和浓度与缓冲材料断面上的平均流速和浓度不一致所导致的分散现象[50]。在对流作用中考虑了通过缓冲材料断面上平均流速产生的核素迁移问题。机械弥散实质上是溶液通过缓冲材料中孔隙的平均流速和浓度的差值导致的核素迁移问题[53]。因此,由机械弥散作用引起的核素迁移通量也可用Fick定律来描述,如式(28)所示。
(28)
式中:Jd,机械弥散通量;Dd,机械弥散系数。
由于分子扩散和机械弥散从引起核素迁移效果上看类似,所以,在实际应用中把分子扩散和机械弥散统称为水动力弥散,水动力弥散系数D为分子扩散系数Dm和机械弥散系数Dd之和,如式(29)所示。
D=Dm+Dd
(29)
以膨润土为基材的集成缓冲材料能够作为人工屏障材料应用于高放废物处置库中,其重要原因之一就是其对放射性核素具有良好的吸附作用。当含有放射性核素的地下水在缓冲材料中发生渗流时,流体与缓冲材料颗粒的接触面促使水中的放射性核素吸附在缓冲材料介质表面上,进而延迟其迁移。在等温线性吸附条件下,缓冲材料对核素的吸附量与溶液中的放射性核素浓度(c)成正比,如式(30)所示。
F=Kdc
(30)
式中:F,缓冲材料对核素的平衡吸附容量,mg/g;Kd,吸附分配系数,mL/mg。
根据普遍守恒原理,利用式(26)—(30),可得式(31)。
(31)
将式(31)两边同除n可得式(32)。
(32)
对于正压流,液体的密度可以表示成压力和温度的函数ρl(pl,T),因此水体密度的微分同水体密度之间的比值存在如下关系(式(33))。
(33)


(34)

(35)
式中:Rd,阻滞因子;D,水动力弥散系数,当水流速度较小时,D可近似为表观扩散系数Da。
2 饱和缓冲材料中核素迁移扩散模型求解及长期阻滞特性分析
模拟多因素耦合作用下核素在饱和缓冲材料中的迁移扩散特征,实质上就是对上述建立的多场耦合迁移扩散控制方程进行求解。这类耦合问题涉及到多过程、多参数的多重耦合,求解过程复杂且难度大。而COMSOL是一款高级数值仿真软件,它是以有限元为基础,通过求解偏微分方程(单场)或偏微分方程组(多场)来解决多场耦合问题[54]。它不仅自带许多经典的物理模块,还支持与MATLAB、AutoCAD等相互导入、自定义PDE模块,能更精准地解决实际工程中的物理问题。因此,考虑到多物理场有限元软件COMSOL Multiphysics具备直接全耦合求解的优点,本次求解控制方程组主要采用内置接口和添加上述守恒方程中的耦合项作为源项相结合方式,并利用课题组前期相关模型实验获得的参数[11],可实现多物理场核素在缓冲材料中迁移扩散行为的直接耦合分析。
2.1 几何模型处理
本课题组自主研制的多场耦合条件下缓冲材料长期阻滞性能Mock-up实验系统主要由双层中空罐体装置系统、数据采集与处理系统、供水/供液控制系统构成(图2)。本工作的几何模型以该实验系统中的多场耦合实验罐体装置为参考,其内腔直径为750 mm,高度为750 mm,模拟固化体的加热器壳体直径为180 mm,高度为180 mm。基于COMSOL多场耦合问题的计算模块,取罐体内腔简化截面作为水力边界,长宽均为750 mm;取加热器外部截面为发热边界,长宽均为180 mm(图3(a))。对简化截面进行网格剖分,采用COMSOL Multiphysics中的四边形网格剖分(图3(b)),并在边界处添加边界层,增加模型的收敛性。

图2 缓冲材料多场耦合长期阻滞性能Mock-up实验系统Fig.2 Mock-up experimental system for long-term retarding performance of buffering materials under multi-field coupling conditions

(a)——几何模型及边界, (b)——模型网格划分图3 数值求解几何模型Fig.3 Numerical solution of geometric model
2.2 内置模块导入
(1) 固体力学接口
在固体力学接口中,添加线弹性材料,指定杨氏模量和泊松比组合,缓冲材料的模型下选择“外部应力”,选择“应力张量(空间)”,然后再添加源项作为耦合项。边界选择辊支撑,限制法向位移,并将1.2节构建的饱和多孔介质系统动量守恒方程式(7)代入该接口。
(2) 多孔介质传热接口
COMSOL中在添加物理场界面下,传热分支下的多孔介质物理场中添加多孔介质传热接口,用来模拟多孔介质中的导热和对流传热。多孔介质中定义的温度方程对应于具有热力学性质平均模型的对流-扩散方程,并同时考虑固体基质和流体性质。当进入多孔介质的温度和流体处于平衡状态时,这个方程有效。如果不是,则使用传热界面中的局部热非平衡接口代替。由COMSOL软件给出的多孔介质传热方程[55]与1.2节构建的饱和状态下的缓冲材料能量守恒方程式(25)联合求解。
在“多孔介质传递属性”中,流体内流速场设为dl·u/Rd,其余参数设为用户定义,“多孔基体”内所有参数设为用户定义,方程中并未考虑体应变对热传导的影响,因此在热源项添加体应变作用项,完成对饱和状态下的缓冲材料能量守恒方程的导入。
(3) 达西定律
“达西定律”接口用来模拟多孔介质孔隙中流体的流动,以压力梯度为主要驱动力的前提下,可用于渗透率和孔隙率均很小且低速运动下的流体或介质进行建模[56]。由COMSOL软件给出的达西方程[55]与1.2节构建的饱和状态下的缓冲材料质量守恒方程式(23)联合求解。
(4) 多孔介质中的稀物质传递
该接口专门用于模拟多孔介质中的运输,包括固相和液相,其中化学物质在多孔介质内有可能受到扩散、对流、迁移、分散、吸附等的影响。该接口支持固相完全不变形或者气相介质不运动的情况。由COMSOL软件给出的方程[55]与1.2节构建的饱和缓冲材料溶质迁移方程式(35)联合求解。
2.3 边界条件与初始值
(1) 温度边界条件
加热器设定为温度边界,恒温90 ℃,罐体外部设置为温度边界,恒温25 ℃。
(2) 位移边界条件
设置缓冲材料边界为法向位移为0,切向可自由活动。位移边界均设置为第一类边界条件(辊支撑边界条件)。
(3) 水力边界条件
水力边界条件设置在加热器边界处,选择压力边界,设为200 kPa,罐体外边界为0 Pa。
(4) 溶质浓度边界

(5) 初始值
根据多场耦合条件下缓冲材料长期阻滞性能Mock-up实验系统所需实验条件、缓冲材料的基本参数,以及实验测定的压实膨润土的初始参数,并参考国内外相关文献[57-60],给出耦合的初始值,结果列入表1。

表1 多场耦合模型初始值Table 1 Initial values of THMC coupling model
2.4 耦合模型参数
本模型采用的缓冲材料力学模型为线弹性模型,缓冲材料的性质参数列入表2。

表2 缓冲材料性质参数Table 2 Property parameters of buffer materials
此外,通过课题组前期相关动态迁移柱实验获得了铀元素在膨润土基缓冲材料中迁移扩散的相关参数:阻滞因子Rd=3.49、饱和渗透系数ks=1.00×10-12m/s和表观扩散系数Da=1.29×10-4m2/a[11]。
2.5 多因素耦合下核素迁移扩散特征及预测分析
利用COMSOL软件内置瞬态求解器,在“直接”求解器中选择“MUMPS”,求解因变量分别为浓度c、压力p、温度T以及(动量方程对应的)位移u,本次研究总计时长为10万年,设置初始步长为0,时间步长为10年,停止时间为10万年,以此达到每10年输出一次结果,直到10万年时停止计算的目的,其他选项使用默认设置。
为探讨在地下水中通过浸润使缓冲层达到饱和后,缓冲材料中铀在不同时间尺度内的迁移范围与迁移距离变化特征,依据上文中的多场耦合作用下核素迁移扩散模型、初始条件、边界条件和计算参数等进行数值模拟。模拟分析结果表明(如图4和图5所示),当废物包装容器破裂并发生迁移的0~1 000 a时间尺度为铀迁移扩散的初期阶段,由于初期阶段缓冲材料对铀的吸附容量大,加之温度对缓冲材料吸附铀的能力有正向影响,所以在多场耦合作用的初期阶段时,核素在缓冲材料中迁移扩散较缓慢,迁移距离随时间增加的幅度均在1 m左右,表现为铀浓度-迁移距离关系曲线比中后期阶段(1万~10万年)的浓度-迁移距离关系曲线陡。
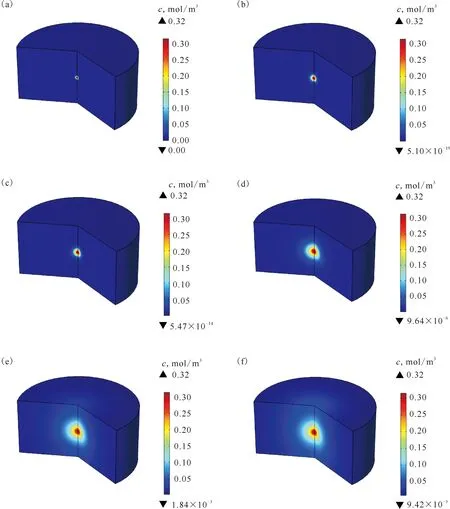
时间,a:(a)——100,(b)——500,(c)——1 000,(d)——10 000,(e)——50 000,(f)——100 000图4 铀在缓冲材料中迁移过程动态变化Fig.4 Variation of radionuclide uranium migration with time in buffer materials

时间,a:1——100,2——500,3——1 000,4——10 000,5——50 000,6——100 000图5 不同时间尺度下铀在缓冲材料中的迁移距离Fig.5 Migration distances of U in buffer materials at different time
随着核素迁移扩散不断进行,在多场耦合作用的中后期阶段(1万~10万年),由于缓冲材料对铀的吸附容量逐渐达到饱和并趋于稳定后,其迁移距离较初期阶段增加更明显,表现为铀浓度-迁移距离关系曲线变缓,迁移距离随时间增幅均在3 m左右。
由此可知,若将缓冲材料的厚度分别设置成2、3 m和4 m,能够分别确保在100、500 a和1 000 a内将铀阻滞在缓冲材料内;若要保证10 000 a内铀不穿透缓冲材料而迁移到处置库围岩地下水中,则需要设置更大厚度的缓冲材料,其厚度至少应为7 m。而Wang等[61]开展了单场环境下铀元素在美国MX-80膨润土中迁移距离数值模拟,结果表明,铀在100、1 000 a和10 000 a等不同时间尺度下分别迁移了0.66、2.1 m和6.6 m。此外,本课题组[11]也在源项释放后100、1 000 a和10 000 a后,对铀在B7AP 型集成缓冲材料(膨润土、凹凸棒石、黄铁矿的质量比为63∶27∶10)中的迁移距离进行了数值模拟分析,结果表明,单场环境下铀在上述不同时间尺度下分别迁移了0.25、0.8 m和3.0 m。可见,在处置库的近场环境条件下,铀在缓冲材料中的迁移扩散过程受到了多物理场耦合作用,导致不同的缓冲材料对铀的长期阻滞效果受到了一定程度的削弱。因此,通过开展多场耦合作用下铀在缓冲材料中的迁移特征模拟研究,能够为高放废物处置库中人工屏障设计及缓冲材料厚度设置等提供科学参考。
3 结 论
(1) 基于混合物理论、连续介质理论、质量守恒、动量守恒、能量守恒及溶质扩散的Fick定律,推导饱和缓冲材料中核素迁移扩散的热-水-力-化耦合控制方程。
(2) 基于多物理场仿真软件COMSOL Multiphysics具备直接全耦合求解的优点,以自主研制的多场耦合条件下缓冲材料长期阻滞性能Mock-up实验系统为几何模型,采用内置接口和添加热-水-力-化耦合控制方程中的耦合项作为源项相结合方式,并在初始条件、边界条件和前期相关模型实验获得的参数的基础上,利用COMSOL软件内置瞬态求解器,实现多物理场耦合作用下核素在缓冲材料中迁移扩散行为的直接耦合分析。
(3) 多物理场仿真软件COMSOL Multiphysics的多因素耦合作用下饱和缓冲材料中核素迁移扩散行为及长期阻滞特性分析表明,初期阶段核素在缓冲材料中迁移扩散较缓慢,迁移距离随时间增幅均在1 m左右;中后期阶段,由于缓冲材料对铀的吸附容量逐渐达到饱和并趋于稳定,其迁移距离较初期阶段增加更明显,迁移距离随时间增幅均在3 m左右;若要保证1 000 a及10 000 a时间尺度内铀不穿透缓冲材料而迁移到处置库围岩地下水中,则需要分别设置缓冲厚度为4 m和7 m。通过开展多场耦合作用下,铀在缓冲材料中的迁移特征数值模拟研究,能够为我国高放废物深地质处置库地下实验室开展1∶1工程尺度的工程屏障设计与安全性能评价提供技术方法和设计依据参考。

