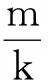探究一道物理竞赛题的多种解法
郑 金
(凌源市职教中心 辽宁 朝阳 122500)
1 试题呈现
(1)试问:此子弹的运动是总在云里?总在云外?还是有时在云里,有时在云外?
(2)求子弹运动轨道的转折点到气体云中心的距离.
(3)讨论子弹运动轨道的形状,并求其运动的周期.
这是一道难度很大的力学竞赛题,突出考查一些重要知识点,目标明确,多点发散,环环相扣,具有很强的综合性与创新性.对于这道题的完整解答详见文献[1],其主要特点是利用万有引力势能曲线和径向有效势能曲线以及扫动面积速率公式进行推断或求解.虽然图像法比较直观,但在根据势能函数描绘势能曲线时难度较大,而且比较繁琐.那么在解题时可否避免画势能曲线呢?是否有更简单的解法呢?通过对试题的深度探究,发现多种巧妙的解法.
2 试题解答
原题有3个设问,其中第(3)问包括两方面,可分为两个小问题,下面对各问分别进行一题多解.
2.1 利用引力势能的取值范围推断子弹运动区域
分析:无论子弹在气体云里运动还是在云外运动,系统的机械能都是守恒的,即E=Ek+U(r)保持不变,由于子弹的动能大于零,则引力势能小于机械能总量,即U(r) 已知子弹的总能量,只要推导出子弹在不同区域受到的引力及其引力势能,再根据引力势能的取值范围分别列出能量不等式,然后求出子弹到气体云中心的距离与半径的关系,即可判断子弹的运动区域. 解法1:利用微积分求引力势能 取无穷远处为引力势能的零点,根据“物体在某点具有的势能等于该物体从所在位置移到势能零点的过程中保守力做的功”可知,在r≥R的区域,引力势能为 在r 已知子弹的总能量 由于子弹的引力势能小于机械能总量,即U(r) (1) (2) 由此可知,子弹到气体云中心的距离总小于气体云的半径,所以子弹总在云里运动. 解法2:利用特殊方法求引力势能 在r≥R的区域,子弹受到气体云的万有引力大小为 选择无穷远处的引力势能为零,根据两个质点的万有引力公式与引力势能公式之间的关系可知引力势能为 在r 跟距离r成正比,则引力在区间r~R上的平均值为 可知子弹从气体云内部所在位置运动到气体云表面的过程中引力做的功为 子弹从气体云表面运动到无穷远处即势能零点的过程中引力做的功为 所以引力势能为 分析:子弹在有心力的作用下做曲线运动,在轨道的转折点处,瞬时速度垂直于矢径,则角动量大小为L=mvr,总能量为 在转动参考系中的总能量为 解法1:利用角动量守恒定律和能量守恒定律 设子弹轨道的转折点到气体云中心的距离为r,瞬时速度为v,由角动量守恒定律可知子弹相对于气体云中心的角动量大小为 由于子弹在云里运动,可知系统的机械能总量为 化简为 联立方程可得 32r4-16R2r2+R4=0 解此方程得 可知子弹运动轨道的转折点到气体云中心的最小距离和最大距离分别为 这表明子弹运动轨道的转折点至少为两个. 解法2:利用径向有效势能的极值条件 子弹在有心力的作用下做曲线运动,角动量保持不变,由于子弹总在云里,则径向有效势能为 在轨道的转折点处,径向速度为零,则径向动能为零,因此有效势能等于总能量,即Ueff=E. 联立方程可得 32r4-16R2r2+R4=0 解法3:利用径向有效势能的取值范围 根据有效势能的取值范围Ueff≤E可知, 化简得 32r4-16R2r2+R4≤0 若以x=r2为自变量,则y=32x2-16R2x+R4的图像是开口向上的抛物线,如图1所示,可知抛物线与横轴相交于两点的横坐标分别为 为了满足y≤0,即函数y=32x2-16R2x+R4取值不大于零,对应自变量的区间为x1≤x≤x2,其等价不等式为 可得 由此可知子弹到气体云中心的最小距离和最大距离分别为 子弹在运动过程中到气体云中心的最小距离和最大距离就是径向运动的转折点到气体云中心的距离. 分析:气体云为质量均匀分布的球体,由对称性可知,无论子弹在云里还是云外,受到万有引力的力心都在气体云的中心,即力心的位置固定不动.由于子弹在有心力的作用下做曲线运动,总在云里运动;而且运动轨道的转折点不少于两个,因此运动轨道不可能是圆周、抛物线或双曲线,只能是椭圆. 解法1:利用对比法分析力心在椭圆中的位置 解法2:利用假设法分析力心在椭圆中的位置 总之,线性正比力的力心位于椭圆轨道的中心,那么长轴的两个端点和短轴的两个端点是轨道的转折点即径向速度为零的点,则转折点共有4个. 分析:对于有心力作用下的曲线运动,由于角动量守恒,则矢径扫动的面积速率恒定,只要求出面积速率以及椭圆的面积,即可求出环绕周期;当力心位于椭圆中心时,在子弹环绕一周的过程中,径向运动通过4个转折点,则径向简谐运动经历两个周期,可知环绕周期等于径向运动周期的2倍.对于线性正比力作用下的椭圆运动,径向运动为简谐运动,只要在平衡点对径向有效势能取二阶导数求出等效劲度系数以及径向运动的周期,即可得到环绕运动的周期. 解法1:利用面积速率求环绕运动的周期 由于力心位于椭圆的中心,则长轴端点和短轴端点对应的矢径都与瞬时速度方向垂直,且矢径的长度分别为半长轴a和半短轴b,对于质点从长轴端点运动到短轴端点的过程,由角动量守恒定律有 mvAa=mvBb 有心力 类似于弹簧的弹力,设椭圆中心即r=0处为等效弹性势能的零点,由机械能守恒定律有 两个方程联立可得 可知子弹经过椭圆顶点处的面积速率为 由于角动量守恒,因此面积速率处处相等. 椭圆的面积为S=πab,可知子弹沿椭圆运动的周期为 由于 所以 解法2:利用有效势能求径向运动的周期 由于子弹在线性正比力的作用下做椭圆运动,则与弹簧振子类比可知,子弹沿径向运动是相对于平衡位置的简谐运动.径向有效势能为 将有效势能函数两边取一阶导数,可得 那么 可知径向简谐运动的周期为 所以子弹环绕周期为 该题原解是利用面积速率公式 得到 利用转折点到气体云中心的距离求出椭圆的面积 由此计算子弹环绕运动的周期为 值得注意的是,环绕运动周期与径向运动周期不同,对应的等效劲度系数也不同,即k≠k′. 特别有趣的是,由线性正比力决定的椭圆运动的周期公式跟简谐运动的周期公式相同,都为
2.2 由方程或不等式求子弹运动轨道转折点位置
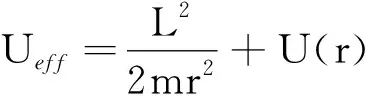
2.3 利用两种方法讨论力心在椭圆中的位置

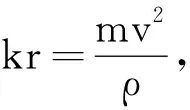

2.4 利用两种方法推导子弹做椭圆运动的周期
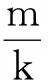
3 结束语