运用等效观深化绳-船模型

何述平 卢嘉鹏 张雯婷

(西北师范大学教育学院 甘肃 兰州 730070)

1 引言

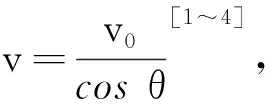
图1 绳-船模型

2 运动分解形式的推证

船的运动为合运动，绳、船连动，连接船的绳端与船的运动物理量(位移、速度)相同，绳端A(或船)为研究对象，运用速度合成法[4]可推证绳端A(或船)运动的3种不同分解形式．

2.1 运动分解形式1

绳端A(或船)运动为沿绳向上分运动v1和垂直绳向下分运动v2的合运动，如图2的运动分解形式1.依据图2和题意(绳缩短速度v0)，有

v1=v0

(1)

v2=v1tanθ

(2)

(3)

由式(1)～(3)，得

v2=v0tanθ

(4)

(5)

式(1)、(4)、(5)分别是绳端A(或船)的分速度v1(方向沿绳向上)、分速度v2(方向垂直绳向下)、合速度v(方向水平向左)大小的表达式[1～4]．

图2 运动分解形式1图示

v1x=v0cosθ

(6)

v1y=-v0sinθ

(7)

v2x=v0sinθtanθ

(8)

v2y=v0sinθ

(9)

再沿水平方向和竖直方向合成，可得

(10)

vy=v1y+v2y=0

(11)

式(10)、(11)表明：合运动vx沿水平向左方向，竖直方向的两分运动v1y和v2y彼此抵消．学生可深入理解绳端A(或船)的分运动与合运动的关系：分运动v1和v2与合运动v相互等效．

2.2 运动分解形式2

绳端A(或船)运动为沿绳向上分运动v3和竖直向下分运动v4的合运动，如图3的运动分解形式2.依据图3和题意(绳缩短速度v0)，有

v3-v4sinθ=v0

(12)

v4=v3sinθ

(13)

v=v3cosθ

(14)

由式(12)～(14)，得

(15)

(16)

及v的表达式同式(5)．式(15)、(16)、(5)分别是绳端A(或船)的分速度v3(方向沿绳向上)、分速度v4(方向竖直向下)、合速度v(方向水平向左)大小的表达式[1，3]．

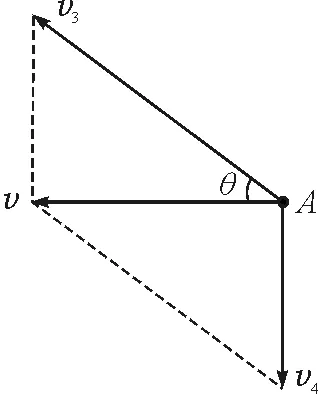
图3 运动分解形式2图示

(17)

(18)

再沿水平方向和竖直方向合成，可得：合运动v3x沿水平向左方向，竖直方向的两分运动v3y和v4彼此抵消．不仅学生可深入理解绳端A(或船)的分运动与合运动的关系：分运动v3和v4与合运动v相互等效；而且学生可能的疑惑“船具有竖直向下的分速度v4，船为什么没有向下运动而潜入水中？”自然而然解除．

2.3 运动分解形式3

绳端A(或船)运动为竖直向上分运动v5和垂直绳向下分运动v6的合运动，如图4的运动分解形式3.依据图4和题意(绳缩短速度v0)，有

v5sinθ=v0

(19)

v5=v6cosθ

(20)

v=v6sinθ

(21)

由式(19)～(21)，得

(22)

(23)

及v的表达式同式(5)．式(22)、(23)、(5)分别是绳端A(或船)的分速度v5(方向竖直向上)、分速度v6(方向垂直绳向下)、合速度v(方向水平向左)大小的表达式．

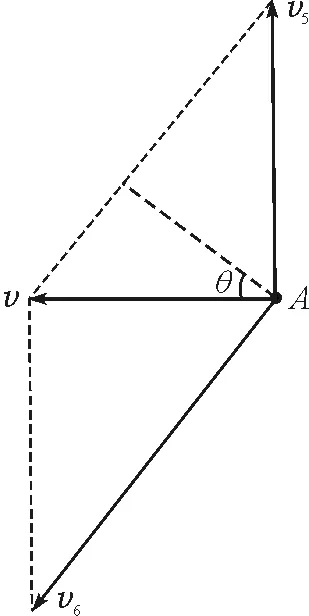
图4 运动分解形式3图示

(24)

(25)

再沿水平方向和竖直方向合成，可得：合运动v6x沿水平向左方向，竖直方向的两分运动v5和v6y彼此抵消．不仅学生可深入理解绳端A(或船)的分运动与合运动的关系：分运动v5和v6与合运动v相互等效；而且学生可能的疑惑“船具有竖直向上的分速度v5，船为什么没有向上运动而脱离水面？”自然而然解除．

上述分解形式的推证过程表明这3种运动分解形式不同(分速度大小、方向不同)，简捷程度为：形式1最简，形式2次之，形式3最繁．

3 分运动形式的等效

绳端A(或船)运动可分解为上述3种形式分运动，并已验证分运动与合运动相互等效；那么，不同形式分运动之间是否彼此等效？

3.1 分运动形式1与2等效

将图3的分速度v4沿绳向上方向和垂直绳向下方向即按图2的v1和v2方向分解，则有

v1=v3-v4sinθ

(26)

v2=v4cosθ

(27)

再由式(15)、(16)可得式(1)、(4)，表明：图3分运动形式2与图2分运动形式1等效．

将图2的分速度v2沿水平向左方向和竖直向下方向分解，有式(8)、(9)；竖直方向添加增量

Δvy=v0sinθtan2θ

(28)

由式(9)、(28)，并参考图3，得

(29)

v2x与竖直向上Δvy合成，由式(8)、(28)得

Δv3=v0tan2θ

(30)

方向与水平向左方向的夹角为θ，即沿绳向上方向；再由图2和式(1)、(30)，得

(31)

式(29)、(31)表明：图2分运动形式1与图3分运动形式2等效．

3.2 分运动形式1与3等效

将图4的分速度v5沿绳向上方向和垂直绳向下方向即按图2的v1和v2方向分解，则有

v1=v5sinθ

(32)

v2=v6-v5cosθ

(33)

再由式(22)、(23)可得式(1)、(4)，表明：图4分运动形式3与图2分运动形式1等效．

将图2的v1沿水平向左方向和竖直向上方向分解，有式(6)、(7)(去掉右侧的“-”号)；竖直方向添加增量

Δvy=v0cosθcotθ

(34)

由式(7)、(34)，并参考图4，得

(35)

v1x与竖直向下Δvy合成，由式(6)、(34)得

Δv6=v0cotθ

(36)

方向与竖直向下方向的夹角为θ，即沿垂直绳向下方向；再由图4和式(4)、(36)，得

(37)

式(35)、(37)表明：图2分运动形式1与图4分运动形式3等效．

3.3 分运动形式2与3等效

将图3的v3沿水平向左方向和竖直向上方向分解，有式(17)、(18)；v3y与v4彼此抵消，竖直方向添加增量

(38)

竖直向上方向，有

(39)

竖直向下方向，有

(40)

v3x与v6y合成，由图4和式(17)、(40)得

(41)

方向与竖直向下方向的夹角为θ，即沿垂直绳向下方向．式(39)、(41)表明：图3分运动形式2与图4分运动形式3等效．

将图4的v6沿水平向左方向和竖直向下方向分解，有式(24)、(25)；v6y与v5彼此抵消，竖直方向添加增量

(42)

竖直向下方向，有

(43)

竖直向上方向，有

(44)

v6x与v3y合成，由图3和式(24)、(44)得

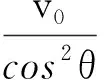
(45)

方向与水平向左方向的夹角为θ，即沿绳向上方向．式(43)、(45)表明：图4分运动形式3与图3分运动形式2等效．

上述推证结果表明：绳端A(或船)的分运动形式1,2,3之间彼此等效；推证过程表明：3种分运动形式的简捷程度是：形式1最简，形式2次之，形式3最繁．至此，不仅3种形式分运动是否彼此等效的学生可能疑惑自然而然解除，而且学生清晰认识到图2分运动形式1最简捷．

4 运动分解与合成的讨论

绳-船模型的绳端A(或船)运动分解形式1,2,3提供了深入理解运动分解与合成的实例，不仅可清晰认识到一个具体运动(速度矢量)可以分解为不同形式的分运动(分速度矢量)，各形式分运动(分速度矢量)既与合运动(速度矢量)相互等效，又彼此等效；而且可顺势推广到任何矢量可以分解为不同形式的分矢量，各形式分矢量既与合矢量相互等效，又彼此等效．鉴于此，或许从矢量分解的任意性(即矢量可以任意分解)和等效性(即各分矢量与合矢量等效，各分矢量之间等效)更益于理解运动分解的多样性．

尽管矢量分解遵从平行四边形定则，但分解方法有正交法(如图2分解形式1)和非正交法(如图3,4分解形式2,3)；由上述运动分解形式的推证和等效知：图2分解形式1最简捷．鉴于此，或许从矢量分解的方法性更益于理解运动分解的简捷性，即运动分解更适宜运用正交法．这就为处理运动(或矢量)分解与合成问题，提供了思维方法的导引．

5 教学建议

基于上述探究，绳-船模型的提高型教学要点为：

(1)若采用“先学后教”模式，学生可能直接采取如下做法.

1)由图1沿水平和竖直方向分解绳缩短速度v0，从而得船速v=v0cosθ的错解[2,3]；则应先确认船的运动是合运动(方向水平向左)，绳、船连动，连接船的绳端的运动物理量(位移、速度)与船的相同，绳端运动为沿绳向上分运动和垂直绳向下分运动的合运动(错解是凭感觉认为：绳端沿绳向上运动，则船的运动与绳端的水平分运动相同)，如图2(严谨推证需依据位移矢量图和运用位移微元法[4])，再由图2依据速度分解与合成求得船速，并检验分运动与合运动等效；

2)由图3运动分解形式2沿水平和竖直方向分解沿绳速度v3，并认为v3=v0，从而得船速v=v0cosθ的错解[3]；则应先确认船的运动是合运动(方向水平向左)，图3与图2比较可知v3>v0，再由图3依据速度分解与合成求得船速(沿水平向左和竖直向上分解v3)，并检验分运动与合运动等效；

3)由图4运动分解形式3沿水平向左方向分解v6，并求得v6=v0cotθ，从而得船速v=v0cosθ的错解；则应先确认船的运动是合运动(方向水平向左)，再由图4依据速度分解与合成求得船速(沿水平向左和竖直向下分解v6)，并检验分运动与合运动等效．

(2)若采用“探究-交流”模式，则做法如下.

1)全班分成3组，每组推证1种运动分解形式，验证分运动与合运动等效，小组代表上台向全班交流、分享：绳端A(或船)运动可以分解为3种不同形式，各形式分运动与合运动相互等效；

2)每组论证2种形式分运动等效，小组代表上台向全班交流、分享：3种形式分运动彼此等效；

3)每组比较3种运动分解形式特点，小组代表上台向全班交流、分享：图2分解形式1最简捷，分解方法为正交法．

6 结束语

运用速度合成法推证了绳-船模型的绳端(或船)运动的3种分解形式，运用等效观念论证了3种形式分运动不仅与合运动相互等效，而且彼此等效，解决了学生理解绳-船模型的可能疑惑；讨论了3种运动分解形式的简捷程度，提出了绳-船模型的提高型教学建议． 既深化了物理知识(速度概念、运动分解与合成规律)，又深化了物理观念(等效观念)、物理方法[速度(或矢量)正交分解法，非正交分解法]．

若引领学生完成上述推证，则学生不仅看到而且做到图2,3,4的分运动彼此等效，体现了“理解”知识、“经历”过程、“培养”方法的教学目标；因此，运用等效观念深化绳-船模型，既可作为提升物理观念、方法及科学思维之科学推理、科学论证的实例，又可作为指向物理核心素养的提高型教学设计实例．