广义勾股定理和广义三角函数
周仲旺
(潍坊学院 数学与信息科学学院,山东 潍坊 261061)
1 广义勾股定理
定理1 对正实数a,b,c,若满足a≤b
证明 对方程ax+bx= cx两边取对数,。令函数则,一方面, 另一方面,,所以存在唯一性成立[1]。令函数当n<1时,所以a,b,c不构成三角形,当n>1时,所以a,b,c构成三角形。令函数,当n<2 时,所以a,b,c构成钝角三角形,当n>2时,,所以a,b,c构成锐角三角形。
用此定理很容易判断一个三角形是钝角三角形、直角三角形还是锐角三角形,且使所谓的勾股数成为历史不再存在。
该定理可以看成广义勾股定理,这样,不光直角三角形才有勾股定理,除底边小于等于腰的等腰三角形外,每个三角形都有一个勾股定理, 也就是说,除底边小于等于腰的等腰三角形外, 每个三角形都对应着唯一一个大于等于 1的实数n,我们把这个实数n称为三角形的秩。对于任意给定的大于1的实数n,秩为n的三角形有一族,像秩为2的(直角)三角形可以看成一族那样,底边小于腰的等腰三角形的秩是正无穷大,这样的三角形显然是锐角三角形(可以认为它的秩大于2),它也构成一族三角形,底边等于腰的等腰三角形即等边三角形是唯一没有秩的三角形,显然,等边三角形也可以看成一族,这族含的三角形最少。任意三角形的秩都可以用matlab算出来。由这个定理可知,以为边的三角形一定是锐角三角形,据此,对任意给定的实数n≥1,能很容易地构造出一个秩为n的三角形,反之,任意给定一个秩为n的三角形,都可以用这个方法构造出来。
2 新正弦新余弦
定义1 对于秩为r的任意三角形ABC,设它的最大角为∠C, , ,ABcBCaCAb= = = , 定义较小角锐角∠A的新正弦,新余弦。注意,只有较小角锐角才有新正弦新余弦,显然sinr(r,A) + c osr(r,A)= 1 (1)。
定理2 对任意秩r>1和任意锐角α,它们的新正弦 s in(r,α) ,新余弦 c os(r,α)存在且唯一。

3 解三角形的简捷方法
根据定理1定理2,三角形的秩和它的较小角唯一决定较小角的新余弦,反过来,三角形的较小角和较小角的新余弦唯一决定它的秩。这样我们可以造个新数学用表,这个表表示的是秩、角、新余(正)弦及其关系(已知这三者中的两者能用计算机通过已造好的表而不是通过方程立即选出第三者,当然,这个表根据方程造),已知秩可以查出较小角的新余弦,已知较小角的新余弦可以查出秩,已知秩和新余弦又可以查出较小角(通常的查锐角的余弦的数学用表,只不过是这里的秩等于2的特殊情况)。进一步,只要给定了三角形的秩r和它的一个较小角α,三角形的另一较小角β和最大角就定了,反之,只要给定了三角形的一个较小角和最大角,它的另一较小角和秩就定了(正弦定理),这样,再造个新数学用表,已知三角形的一个较小角和最大角就能算出它的另一较小角接着查出它的秩,已知三角形的秩和一较小角,就能查出它的另一较小角接着算出它的最大角。这两个新数学用表可以在计算器上通过把余弦函数反余弦函数扩展成为五个新函数下面是这两个新数学用表的重要应用之一。
例1 设三角形ABC的秩是3,AC=3,BC=4,试求它的最长边AB。
解AB3=AC3+BC3= 33+ 43= 9 1,所以最长边AB≈ 4.498。假如要求这个三角形的三个角,只要有个新数学用表,求出新余弦后查查表就行了。
例2 设三角形ABC的秩是4,,最长边AB=6,试求这个三角形的另外两边AC,BC和另外两角∠B,∠C。

例3 设三角形ABC的秩是4,,试求这个三角形的另外两个角∠B,∠C。
例4 在三角形ABC中,试求三角形ABC的秩, 的长,∠C的平分线CD的长及AD,BD的长。
解 设三角形ABC的秩为r,则用matlab求得r≈1.6,

注:假如有个新数学用表,这个题完全可以查表解决,即已知两个较小角可以查出这个三角形的秩,然后再查出较小角的新余弦或新正弦,最后极易求出三角形的边长和角的平分线长!这个解法也说明了已知三角形两角一边时,如何使用查表的方法解三角形。
当已知三角形两边一角时,只要这个角不是三角形的最大角,就可以根据新三角函数使用查表的方法解三角形(其实,即使这个角是三角形的最大角,也可以使用查表的方法,不过,本文不研究这个问题)。当已知三角形三边时,可以先用matlab求出它的秩,然后根据新余弦查查表就能查出它的两个较小角,这比用余弦定理正弦定理好。
总之,引进三角形的秩,在已知三角形的两角一边、两边一角或者三边的情况下,解三角形基本上查查表就行,在其它情况下,更是如此,由此可见三角形的秩的重要作用。
4 三角形的秩的几何意义
秩为r的三角形最大角∠C的两邻边为a,b(a≥b) ,∠C的余弦所以r越大cosC越大∠C越小。当秩等于1时,三角形的两边a,b的夹角最大,是180度,随着秩的增大,三角形的两边a,b夹的三角形的最大角逐渐变小,当秩趋向于正无穷大时,三角形趋向于一个以a为腰以b为底的等腰三角形,这时三角形的两边a,b夹的三角形的最大角达到最小,若底边再等于腰,三角形的最大角达到最小值60度。也就是说:以三角形最大角对应的顶点为圆心以最小边为半径画个圆,当最小边的另一端点在这个圆上移动且三角形的其它两顶点固定时,这样得到的钝角三角形占这个圆的四分之一,而锐角三角形至多占这个圆的十二分之一,从这个意义上说,钝角三角形比锐角三角形多,尽管钝角三角形比锐角三角形多,可钝角三角形的秩在区间(1,2)上,而锐角三角形的秩在区间(2,+∞)上。
根据上面分析,我们可以用三角形的秩判断三角形的形状,即三角形的秩越小越接近于平角三角形,秩越大越接近于等腰三角形。例如:秩为1.01的三角形非常细长,基本上是平角三角形,直角三角形的秩为2,秩比较大,它就比较像等腰三角形,秩为9的三角形基本上是等腰三角形。
5 广义三角函数理论
定义2 在平面在直角坐标系中,从坐标原点O出发的一条射线与x轴的正向的夹角为x,在射线上取一点B,B的坐标为(p,q),在 轴上取一点A,其坐标为(z,0),设三角形OAB的秩为r,令当q≥0时,令当q<0时,令这样,对任意角x都定义了它的新余弦新正弦,由此引入了关于自变量x(r视为常数)的新余弦函数和新正弦函数称为广义三角函数,当r=2时,就是通常的余弦函数正弦函数,不难看出新余弦函数新正弦函数也都是以2π为周期的周期函数,其中OB必须是三角形OAB的最长边,
定理 3[2]若函数F(x,y)满足下列条件:
(ⅰ)F(x0,y0) = 0 (通常称为初始条件) ,
(ⅱ)F在以P0(x0,y0)为内点的某一邻域D⊂R2上连续,
(ⅲ)F在D内存在连续偏导数Fx(x,y),Fy(x,y),
(ⅳ)Fy(x0,y0) ≠ 0。
则(ⅰ)存在点 的某邻域U(P0)⊂D,在U(P0)上方程F(x,y)= 0 唯一地决定了一个定义在某区间(x0−δ,x0+δ)上的函数y=f(x),使得当x∈ (x0−δ,x0+δ)时, (x,f(x)∈U(P0),且
(ⅱ)f(x)在 (x0−δ,x0+δ)上连续,有连续导函数,且
定理4 当r>2时,新余弦函数y(x) = c os(r,x)在(0,)上连续,具有连续导函数且
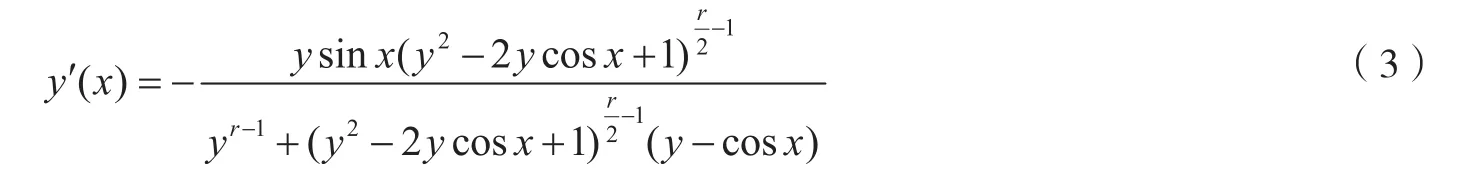

注:此定理不难推广到区间(−∞,+∞)上。
根据(1)(2)(3)式,不难得到
定理 5 当x是锐角时
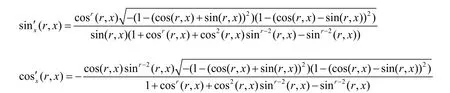
所以,当r>2时,cos(r,x) ,sin(r,x)的单调性很清楚了。
注:当x是锐角时,显然 (c os(r,x) + s in(r,x) )2> 1 ,(cos(r,x) − s in(r,x))2<1。
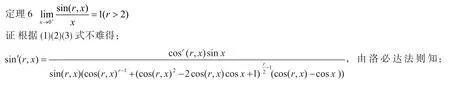
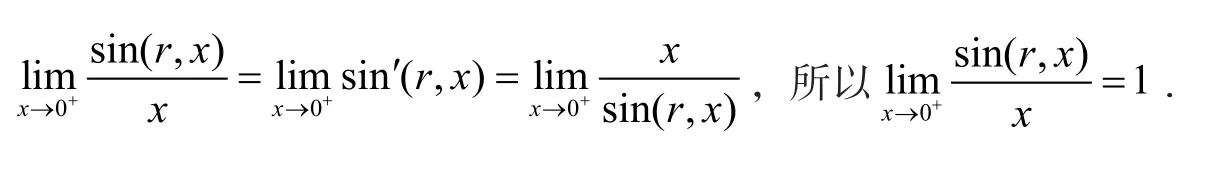
注:当1 值得一提的是:根据(2)式,在原来基本初等函数的意义下,新余弦函数新正弦函数基本没有显示式,但反新余弦函数反新正弦函数都有显示式。 经过简单计算得:sin(3,0.3) = 0.297,sin(3,0.75) = 0.69,sin(3,1.25) = 0.96 sin(3,1.5) = 0.999,cos(3,0.3) = 0.99,cos(3,0.75) = 0.87,cos(3,1.25) = 0.48,cos(3,1.5) = 0.111再根据单调性,不难作出sin(3,x),co s (3,x)的图像,它与sinx,cosx的图像差不多。 经过简单计算得:sin(1.5,0.27) = 0.27,sin(1.5,0.914) = 0.82,sin(1.5,1.28) = 0.97 sin(1.5,1.43) = 0.99596,cos(1.5,0.27) = 0.901,cos(1.5,0.914) = 0.409,cos(1.5,1.28) = 0.121 cos(1.5,1.43) = 0.0332,π2 = 1.57,再根据单调性和凸性,不难作出sin(1.5,x) , co s (1.5,x)的图像,它与sinx,cosx的图像差不多,只不过cosx的图像上凸而cos(1.5,x)的图像下凸。 综合以上研究,基本上搞清楚广义三角函数了。 所有的新正弦函数新余弦函数都应看成基本初等函数,sinx,cosx其实就是sin(2,x) ,cos(2,x) ,sinx, cosx写为sin(2,x) ,cos(2,x)更科学。cos(r,x)和cosx间有关系(2),所以新基本初等函数实际上只有两个,即对一个固定的r, sin(r,x)和cos(r,x)。根据(2),cos(r,x)一般不能由cosx表示,但cosx都可由cos(r,x)表示,所以,凡是能用正弦余弦表示的函数必能用新正弦新余弦表示,但是能用新余弦新正弦表示的函数一般不能用余弦正弦表示,这说明广义三角函数是比三角函数更基本更有意义的函数!广义三角函数在物理学以及其他学科中都有重要应用,例如在水波、声波、简谐振动和交流电中,这些问题用广义三角函数研究比纯粹用三角函数研究更精确更好。另外,广义三角函数能使导弹命中率更高吗?广义三角函数能使卫星定位更精确吗?这些问题有待专家进一步研究,凡是能用三角函数研究的实际问题都能用广义三角函数研究,这只要把三角函数中隐含的秩2改成广义三角函数中的秩r即可。

