以“思维进阶”为导向的高考数学二轮复习策略
曹玉梅
(福建省厦门外国语学校 361000)
随着高考改革的深入,高考试题已由“解答试题”转向“解决问题”.“解决问题”的关键在于思维.在高中数学一轮复习中,大多数教师都是根据知识体系进行教学,以知识框架掩盖学生思维发展框架的现象较为普遍,以思维为主线的教学往往处于低水平状态.大部分学生虽然初步建立了知识体系,但不能完全建立知识间的纵横联系.二轮复习则起着承上启下的作用,是学生形成系统化、条理化知识的重要时期,也是促进他们内化知识、并不断提升知识迁移能力、阅读能力、分析问题和解决问题能力的关键期.因此,在二轮复习中,促进学生的思维方式、思维结构、思维品质向高层次发展,实现思维能力的进阶,是提高数学学习力、理解力和应用力的可行路径.
1 体系重建,方法重构,增进聚合与发散思维融合
聚合性的思维是从已有的知识储备和经验之中找到能够解决问题的有一定方向性、条理性的一种思维方式,它可以让我们对所掌握的知识、方法得以巩固.而发散性的思维则是针对同一个问题从不同的途径和角度来进行假设、探究和分析.
在二轮复习中,我们可以引导学生在解决问题的过程中对一轮复习中的核心概念、思想方法再次进行提炼,“聚合”成完备的知识、方法体系,再对问题的解法、结果进行发散思考,增进聚合与发散思维融合.笔者在二轮复习中,以下题为例对学生进行知识、方法和思维的聚合与发散.
例1①tanB=2tanC,②3b2-a2=12,③bcosC=2ccosB三个条件中任选一个,补充在下面问题中的横线上,并解决该问题.
问题:已知△ABC的内角A,B,C及其对边a,b,c,若c=2,且满足____.求△ABC的面积的最大值.


随后,笔者引导学生跳出三角恒等变换与解三角形这一知识模块,向其它模块迁移.先请学生继续思考:本题的所有已知条件其实就是“c=2,且3b2-a2=12”.这两个条件是不是说明此三角形隐藏了某种几何特征?
为此,笔者先引例铺垫:△ABC中,c=2,且①b=2a(或者②b+a=2c),求△ABC的面积的最大值.学生简单作图后发现,△ABC的几何特征是“顶点A、B固定,顶点C是动点,它与定点A、B的距离之比(和)为定值”,于是很快得出“三角形的顶点C在圆(椭圆)上”.此时,他们的思维也逐渐发散开来,开始猜想——这“隐藏的几何特征”虽然不能直接看出,但可以通过“坐标法”求出.于是,以AB所在直线为x轴、AB的中垂线为y轴建立平面直角坐标系,易知顶点C(x,y)满足:3[(x+1)2+y2]-[(x-1)2+y2]=12,化简得:(x+2)2+y2=9.显然,当顶点C运动至点(-2,,3)处时,△ABC面积取得最大值3.
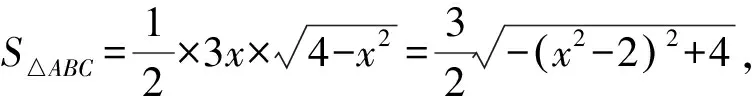
这样,学生在探寻不同的解决方案的过程中,知识体系、思想方法得以完善,更重要的是,思维在聚合——发散——聚合中得以锻炼.
2 执果索因,反向思考,增强逆向思维训练
逆向思维是在研究问题时从反面观察事物,做与习惯性的思维方向完全相反的探索.在中学数学教学中,无论是逆运算和逆定理,还是反例法、反证法、分析法等,逆向思维的思想无处不在,可以说逆向思维是贯穿整个中学阶段的一种重要思维方式.下面笔者例举一个数列放缩与函数相结合问题来说明逆向思维的运用.

(1)判断f(x)的单调性;

3 跳出常规,消除“思维定式”,升华“微专题”的应用,培养创新思维
“微专题”是从具体考点开始研究,将其所涉及的基本概念、原理、解题方法通过题组形式呈现,它能帮助学生内化知识,掌握解决此类问题的“通法”.但是,它的双重性在于:它既可能启发学生总结规律,也可能导致僵化的思维:因为学生仅仅获得熟悉情景下的数学问题的解决能力,却无法自主分析和解决新情景下的数学问题.


总之,“数学是思维的体操”.虽然高考改革、生情的变化、教学资源的差异,都会使二轮复习的策略随之改变.促进学生思维良性发展,既是我们数学课堂教学的灵魂,也是保证复习效率的关键.坚持以思维进阶为导向来实施教学,不仅仅是培养学生解决数学问题的能力,更是通过数学思维训练,帮助学生形成良好的思考习惯和多元思维能力,从而提升创新思维能力,使其成为具有终身学习能力的人.

