填充二氧化碳的低温真空管道绝热性能研究

许张良 谭宏博 吴 昊

(西安交通大学能源与动力工程学院 710049 西安)

1 引 言

CO2冷凝真空绝热是基于CO2低温冷凝获得夹层真空度的一种绝热形式,利用CO2在液氮温区以下饱和蒸气压低的特性,向低温管道真空绝热层内充入高纯CO2,在低温下凝华形成深冷霜,其对真空夹层内的残余气体分子有吸附作用,提高真空度、使夹层内气体导热和对流被大幅削弱,从而使该结构绝热效果接近高真空多层绝热[1]。郑建耀等人[2]介绍了填充CO2的低温容器冷凝绝热机理,通过实验论证了选用CO2在液氮温度下可满足冷凝真空绝热的要求;姚娜等人[3]用量热法进行实验研究发现:CO2冷凝真空绝热层的绝热效果优于聚氨酯塑料绝热层,实测热导率仅为0.003—0.004 W/(m·K)。聚异氰脲酸酯硬泡(PIR)是一种在深冷绝热领域使用较广泛的材料,可作为LNG 输送管道或LNG 加注站绝热材料,它能够在较低温度下保持优越的绝热性能,但其敷设厚度对空间需求较大,因此本文拟研究填充CO2的粗真空条件下的绝热结构,可对PIR 硬泡绝热层进行部分替代。据测算,CO2冷凝真空绝热层的表观热导率远低于PIR 硬泡绝热层,其绝热性能远优于普通堆积绝热和真空粉末绝热。同时,CO2冷凝真空绝热管道结构简单、自重轻、体积小,将其应用于低温液体输送管道具有广阔的应用前景。

2 CO2 冷凝真空绝热层表观热导率计算模型

以有填充材料的CO2冷凝真空绝热板(Vacuum Insulation Panel,简称VIP)为例,首先针对填充芯材为玻璃纤维的真空绝热板,构建热导率预测模型:热量传递主要包括芯材固体骨架的导热、填充气体的导热、固体骨架与绝热板之间的辐射传热,其中前两者的贡献用气固耦合热导率λgs表征,而第三者的贡献用辐射热导率λr表征。因此,真空绝热板表观热导率的总表达式为:

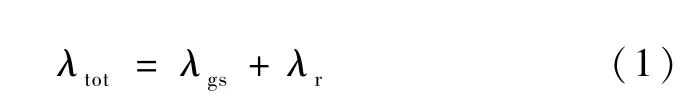
由于纤维各层厚度相同,层内纤维均呈随机布置,根据传热学和统计学基本原理可知,其相邻两层纤维的等效热导率与纤维芯材的有效热导率是相同的[4]。当热流流经不同纤维层时,热量传递方式可分为3 种[5]:(1)纤维之间的热量传递(可分为垂直接触和平行接触两种方式);(2)纤维与气体之间的热量传递;(3)气体与气体之间的热量传递。

纤维与纤维间的热导率λff可以表示为[5]:

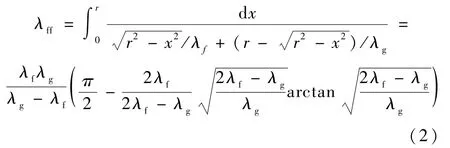
纤维与气体间的热导率λfg可以表示为[5]:

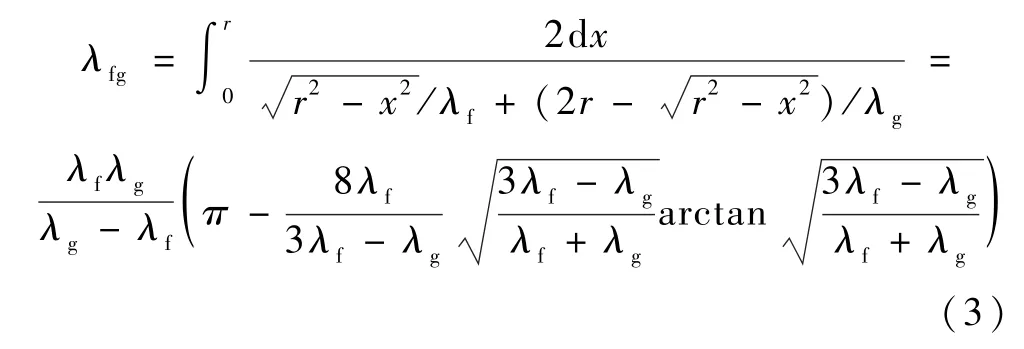
式(2)和(3)中:r为纤维半径,m;x为积分变量,表示纤维直径方向上的坐标,m;λf为玻璃纤维基体的热导率,W/m·K;λg为气相热导率,W/m·K。

气体与气体之间的热导率即为气相热导率λg。

Kaganer[6]针对两个无限大平行平板间的气体导热提出了Kaganer 气相热导率计算模型,其表达式为:

式中:fv为纤维体积分数;γ为常温常压下气体的比热容比;α为相容系数,空气和CO2均为简单非极性分子,取α=1;λ0为自由空间中静止气体在常温常压下的热导率(也称常规热导率),W/m·K;Kn为Knudsen 数。

不同纤维层间的气固耦合热导率为:

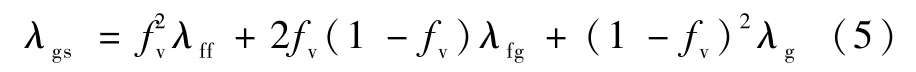
假设多孔材料是光学厚介质,真空绝热板内的辐射热导率可按照下式计算[7]:

式中:σ为斯特藩-玻尔兹曼常数,W/(m2·K4);T为真空绝热板温度,K;ρt为玻璃纤维芯材的密度,kg/m3;Ke为玻璃纤维的Rosseland 平均比消光系数,m2/kg。

当真空绝热板内填充二氧化硅气凝胶时,表观热导率的计算方法与填充玻璃纤维时不同。二氧化硅气凝胶颗粒的热导率λp可按下式计算[8]:

式中:λf为二氧化硅基体的热导率,W/(m·K);l为二氧化硅声子的平均自由程,m;dp为气凝胶颗粒直径,m。

Bi 等人[9]从几何模型的角度推导了二氧化硅气凝胶的气固耦合热导率表达式:

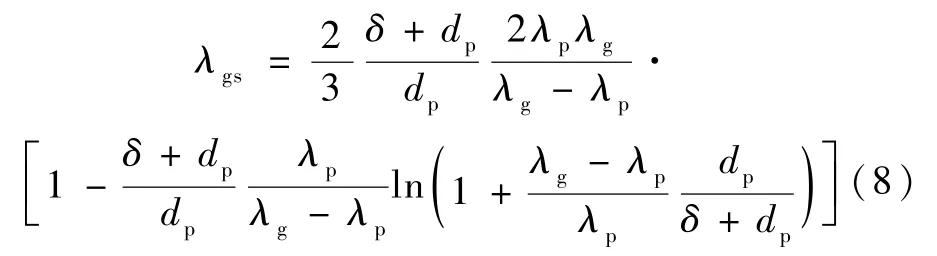
式中:δ为气凝胶孔隙的平均直径,m;λg为气相热导率,W/(m·K),计算方法同式(4)。在这里忽略纳米材料骨架对气体分子平均自由程的限制作用。

式(8)中的气固耦合热导率只考虑了垂直于气凝胶骨架方向的导热,而没有考虑气凝胶骨架自身传热以及单纯的气体导热,因此除气固耦合热导率λgs和辐射热导率λr之外,还需要加上气凝胶骨架热导率λs和气相热导率λg才能构成二氧化硅气凝胶有效热导率的表达式[10]:

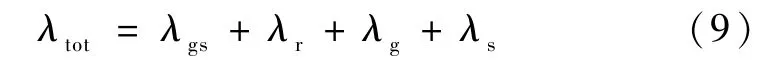
式中:λs为二氧化硅气凝胶骨架热导率,W/(m·K),其表达式如下[9]:

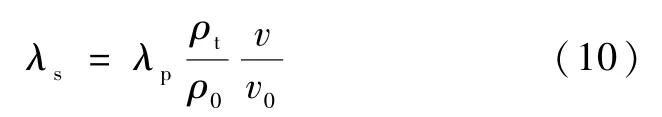
式中:ρt为气凝胶的密度,kg/m3;ρ0为气凝胶固体骨架的密度,kg/m3;v为二氧化硅气凝胶材料整体的声速,m/s;v0为二氧化硅气凝胶骨架的声速,可认为是二氧化硅声子的运动速度,m/s。

CO2凝华之后会形成深冷霜,填充在材料的孔隙中,使真空绝热板的真空度提高,气相热导率减小,进而影响总的表观热导率。本文用克劳修斯-克拉贝隆方程获得CO2温度与饱和蒸气压的关系,从而依次修正气体填充压力、纤维体积分数、孔隙率和表观热导率。利用文献[11] 给出的温度位于77.04—102.50 K 之间时二氧化碳的温度与饱和蒸气压数据,得到以下关系:

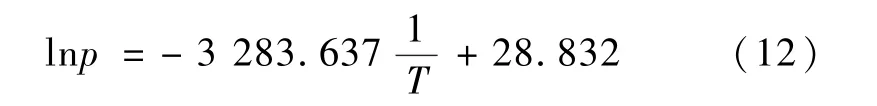
对于玻璃纤维材料,可得到修正纤维体积分数FV与初始纤维体积分数fv之间的关系为:

式中:p为二氧化碳气体在温度T下的饱和蒸气压,Pa,其取值方式由式(12)给出;p0为二氧化碳气体的初始填充压力,Pa;ρ∗为二氧化碳冷凝霜的密度,kg/m3;Rg为二氧化碳的普适气体常数,J/(kg·K)。当饱和蒸气压p小于初始填充压力p0时,需要使用式(13)修正纤维体积分数;若饱和蒸气压p大于初始填充压力p0,二氧化碳气体按照初始填充压力充入绝热层后即保持该压力不变,无需修正纤维体积分数。

相应地,孔隙率可按照下式修正:

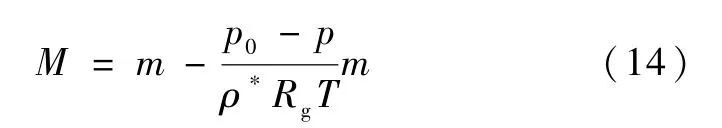
式中:M为修正后的孔隙率,m为初始孔隙率。

管道真空绝热层的厚度极小,远小于绝热层内、外壁的周长,因此可将内、外壁视为两块无限大平行平板,Kaganer 气相热导率模型适用,而辐射热导率和材料基体热导率与绝热结构无关,故在计算低温真空绝热管道的表观热导率时,可直接利用上述真空绝热板的计算模型。

3 模型验证

选取平均直径6 μm、孔隙率95% (纤维体积分数5%)的玻璃纤维填充真空绝热板,填充气体选为空气,绝热板的平均温度为298 K。应用以上计算模型得到真空绝热板的表观热导率,并与文献[13]进行比较,结果如表1 所示。

从表1 的结果可以看出,本研究的计算结果与文献[13]的测量结果吻合较好,误差基本在±10% 以内,且小于文献[12]中热导率预测值与测量值偏差,说明本研究提出的热导率计算模型预测精度较好,总体优于文献[12]的预测结果。

表1 真空绝热板表观热导率随空气压强的变化关系Table 1 Relationship between VIP’s equivalent thermal conductivity and air pressure

4 结果分析

4.1 填充空气与二氧化碳的真空绝热层绝热性能比较

选用孔隙率95%、直径6 μm 的玻璃纤维作为填充材料,比较填充空气或填充CO2的真空绝热层的绝热性能,结果如图1 所示。由图可知,在相同的温度和气体压力下,填充CO2的真空绝热层的绝热性能高于用空气填充的真空绝热层,且温度越低,填充CO2的绝热层优越性更加显著:例如当填充压力为10 Pa,绝热层的平均温度为80 K 时,用空气填充的绝热层的热导率为1.401 mW/(m·K),而填充CO2的绝热层的表观热导率为0.052 mW/(m·K),仅为填充空气的3.71%。

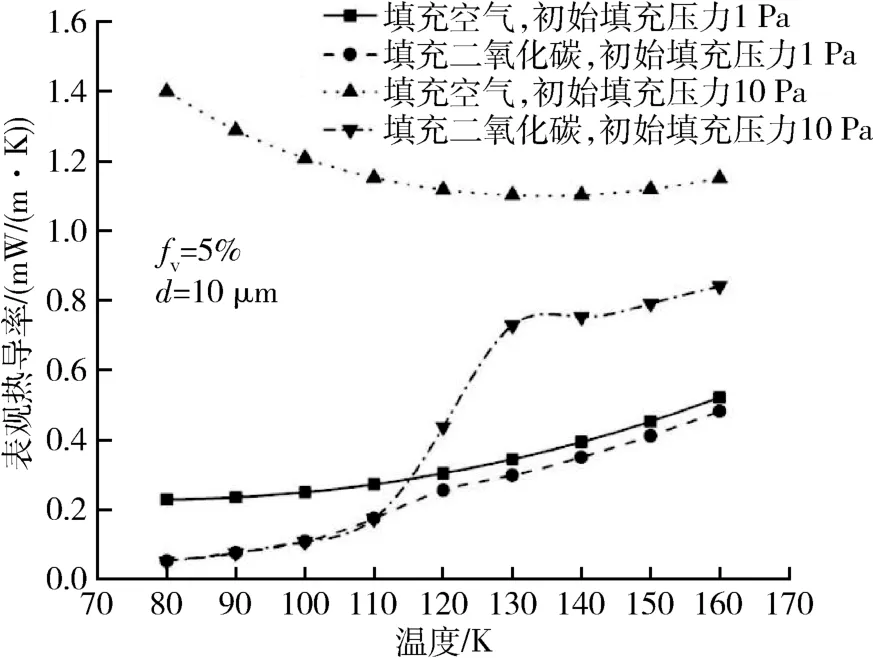
图1 填充空气与二氧化碳的绝热层绝热性能比较Fig.1 Comparison of thermal insulation performance between insulation layers filling with air and CO2

当气体的初始填充压力为1 Pa,绝热层的平均温度为100 K,填充材料选用直径分别6 μm 和12 μm的玻璃纤维时,比较当纤维体积分数变化时,填充空气与CO2的绝热层的绝热性能。

图2 显示,纤维直径对热导率的变化趋势没有影响:对于填充空气的绝热层,随着纤维体积分数的增加,热导率呈现上升趋势,而对于填充CO2的绝热层,随着纤维体积分数的增加,热导率先下降后上升,总体变化不大,且填充CO2的绝热层性能更佳,在初始纤维体积分数处于10%—15% 之间时,填充CO2的绝热层的表观导热系数最小。

图2 初始纤维体积分数和纤维直径对绝热性能的影响Fig.2 Influence of origin fiber volume fraction and diameter on insulation performance

4.2 填充不同材料的真空绝热层绝热性能比较

当绝热层内壁温度T1=130 K,外壁温度T2=150 K 时,变化初始填充压力,比较填充不同材料时绝热层的表观热导率。

由图3 可见,当绝热层内填充玻璃纤维或二氧化硅气凝胶时,表观热导率可达到1 mW/(m·K)以下,其中填充玻璃纤维的真空绝热层的表观热导率较低,当气体初始填充压力为0.1 Pa 时,表观热导率仅为0.3 mW/(m·K)。真空绝热层填充玻璃纤维时的表观热导率较低的原因是:玻璃纤维只需要考虑气固耦合导热和辐射传热,而二氧化硅气凝胶由于具有比较复杂的三维颗粒堆积分形结构,还需要考虑气凝胶骨架自身传热以及气体导热。

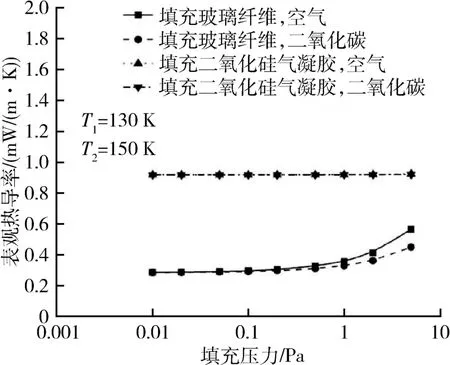
图3 填充不同材料时绝热层的表观热导率Fig.3 Equivalent thermal conductivity of the insulation layer filling different materials

图3 还表明,当绝热层的填充材料是二氧化硅气凝胶时,相对于空气,采用CO2作为填充气体对绝热性能的改善不明显;而当绝热层的填充材料是玻璃纤维时,在气体初始填充压力高于0.1 Pa 时,相对于空气,采用CO2气体填充能够显著改善绝热性能。出现上述现象的原因可能是玻璃纤维与二氧化硅气凝胶的微观结构不相同,导致传热特性不相同:填充材料是二氧化硅气凝胶时,气相热导率占比很小,对气固耦合热导率的影响也很小;而以玻璃纤维作为填充材料时,由于玻璃纤维孔隙率较高,气体与气体之间传热概率增加,随着气体初始填充压力的增加,气相热导率明显增大,而气相热导率在很大程度上影响气固耦合热导率。

4.3 不同填充压力下真空绝热层的绝热性能比较

针对内径0.06 m,外径0.1 m,长10 km 的输送管道,管道内壁温度为120 K,外壁温度为300 K,将管道的绝热层内均匀填充孔隙率95%、直径6 μm 的玻璃纤维,并填充压力为1 Pa 的CO2气体。根据计算模型,可以得到真空绝热层的表观热导率λeff为0.985 mW/(m·K),而在该温度下PIR 硬泡的导热系数为0.024 mW/(m·K),因此填充玻璃纤维的CO2冷凝真空绝热层的绝热性能远优于PIR 硬泡绝热层。

保持管道的结构尺寸,内、外壁温度和填充材料不变,改变二氧化碳气体的填充压力,探究填充压力对CO2冷凝真空绝热层绝热性能的影响,如图4所示。

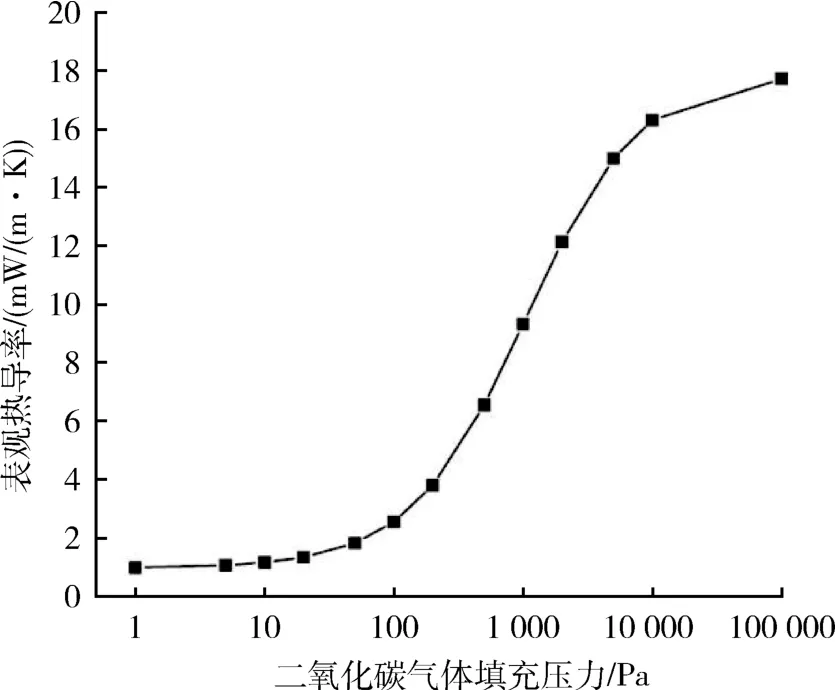
图4 二氧化碳冷凝真空绝热层的表观热导率随CO2 填充压力的变化关系Fig.4 Relationship between filling pressure and equivalent thermal conductivity of CO2 condensation vacuum insulation layer

由图4 可知,随着气体填充压力的增加,CO2冷凝真空绝热层的表观热导率呈现先快后慢的增加趋势,当填充压力处于100 Pa 至10 000 Pa 之间时,增加的十分迅速,原因是在气体填充压力升高的过程中,气体由自由分子状态逐渐转变为连续介质状态。一般用克努森数Kn描述气体的状态[13]:

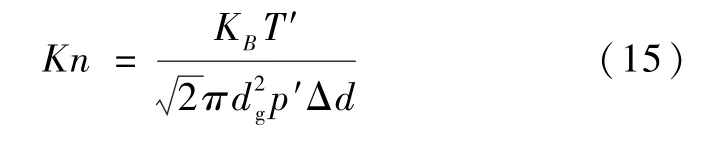
式中:KB为玻尔兹曼常数,KB=1.38 ×10-23J/K;T′为真空绝热层的平均温度,K;p′为最终的气体填充压力,Pa;dg为气体分子直径,m;Δd为特征尺度,这里取为填充材料玻璃纤维的直径,m。当气体填充压力为100 Pa 时,Kn=9.98 ＞1,气体处于自由分子状态[13],气体分子导热是唯一的传热形式;当气体填充压力为10 000 Pa 时,Kn=9.98 ×10-3＜0.01,气体处于连续介质状态[14]。当填充压力上升时,气体分子之间碰撞以及气体与固体分子之间碰撞的概率增大,气体分子状态的改变导致气体与固体之间的对流换热加剧,因此表观热导率大幅上升。

当填充压力处于1 Pa 至100 Pa 之间时,CO2凝华得到的深冷霜较多,其吸附绝热层内的残余气体,真空度提高,气固耦合导热和对流传热被削弱。当填充压力为100 Pa 时,表观热导率为2.553 mW/(m·K),约为同温度下PIR 硬泡绝热层的1/10;当填充压力为500 Pa 时,表观热导率为6.555 mW/(m·K),约为同温度下PIR 硬泡绝热层的1/4。从应用层面来说,只需填充不超过100 Pa 的CO2气体,即可满足绝热要求;同时,填充粗真空状态下的CO2气体,可使绝热层的真空度更容易维持,减少抽空时间和成本。

5 结 论

首先针对真空绝热板和有填充材料的真空绝热层,建立了表观热导率理论计算模型,最后比较不同填充条件下管道绝热层的绝热性能,探讨了LNG 输送管道使用二氧化碳冷凝真空绝热层的可行性。研究结论如下:

(1)通过比较填充空气和CO2两种气体的真空绝热层的绝热性能可知:在低温下,当其他条件相同时,填充CO2的真空绝热层的绝热性能优于填充空气的真空绝热层;当CO2气体的填充压力小于10 Pa,真空绝热层温度低于150 K 时,若选用直径6 μm、孔隙率为90%—95% 之间的玻璃纤维,真空绝热层的表观热导率可控制在0.1 mW/(m·K)以下。

(2)在一定的CO2气体填充压力和温度下,用玻璃纤维填充的真空绝热层绝热性能最优;当绝热层平均温度为140 K,气体填充压力为10 Pa 以下时,填充玻璃纤维的表观热导率可控制在0.3 mW/(m·K)以下。

(3)对于平均温度为210 K 的LNG 输运管道绝热层而言,CO2冷凝真空绝热层相较于PIR 硬泡绝热层具有优异的绝热性能,当气体填充压力为100 Pa时,其表观热导率约为同温度下PIR 硬泡绝热层的1/10,填充粗真空状态下的CO2气体即可使LNG 管道满足绝热性能要求;在低温液体长距离输送管道上应用CO2冷凝真空绝热可减少抽空时间和成本,使管道绝热层处于粗真空状态,同时保持较好的绝热性能,因此CO2冷凝真空绝热在低温液体管道上具有广阔的应用前景。