Green’s function Monte Carlo method combined with restricted Boltzmann machine approach to the frustrated J1–J2 Heisenberg model
He-Yu Lin(林赫羽), Rong-Qiang He(贺荣强), and Zhong-Yi Lu(卢仲毅)
Department of Physics,Renmin University of China,Beijing 100872,China
Keywords: restricted Boltzmann machine,Green’s function Monte Carlo,frustrated J1–J2 Heisenberg model
1. Introduction
In recent years, machine learning (ML) has been extensively used in physics.[1–4]In Ref. [5], it was proposed to represent the wave functions of quantum many-body systems by a neural network — the restricted Boltzmann machine(RBM).[6]And the transverse Ising and Heisenberg models were then studied. The obtained ground-state energies can be more accurate than the ones by state-of-the-art numerical algorithms. The RBM was also shown to be capable of describing the long-range correlations of quantum systems.[7]Other studies for representing the ground states of one- and twodimensional models with the RBM variational ansatz[8–10]showed that it could describe ground states and low-lying excited states accurately.
Despite the RBM can perform well for a number of quantum many-body models, it is demonstrated that there are limitations on its expressive ability as a shallow neural network.[11]Here, we propose to adopt the Green’s function Monte Carlo(GFMC)method[12,13]to improve the expressive ability of the RBM architecture. The purpose of this paper is to present an investigation in which we implement the GFMC based on an RBM guiding wave function preliminarily optimized by the variational Monte Carlo (VMC) method, here referred to simply as GFMC+RBM method,and then explore its effectiveness.
Considering that the quantum Monte Carlo method is subject to a severe sign problem when applied to the frustratedJ1–J2Heisenberg model on a square lattice, we thus take this model to demonstrate the effectiveness of the GFMC+RBM method. We deliberately benchmark the implemented GFMC+RBM method on a small square lattice with exact diagonalization method, considering its validity, efficiency, and accuracy. Then, for a 6×6 square lattice, we make comparisons of the ground-state energies between the GFMC+RBM method and the pure RBM to illustrate the performance of the method. Finally, we show the spin structure factors of the two methods to determine whether the GFMC+RBM method can capture physical properties of the system.
2. Model,method,and implementation
The frustratedJ1–J2Heisenberg model is a typical model with sign problem, which is defined by the following Hamiltonian:

whereSi(S=1/2)is a spin operator at siteion a square lattice,〈···〉and〈〈···〉〉indicate pairs of the nearest and nextnearest neighbour sites,respectively.
In this paper,we setJ1=1.WhenJ2=0,the system is in a Neel antiferromagnetic (AFM) long-range order.[14,15]And whenJ2≫J1, the system is in a well established collinear AFM state.[16,17]The intermediate regimeJ2/J1≈0.5 is a phase transition regime with high frustration. Although there have been a lot of studies about characteristics of this regime,[18–21]till now a definitive conclusion has not been established.
Properties of the phase transition are charaterized by the spin structure factor which is defined as follows:

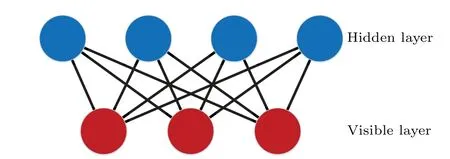
Fig.1. The architecture of the restricted Boltzmann machine. The blue dots in the upper layer denote the hidden neurons, and the red dots in the bottom layer represent the visible neurons.
Since there is no coupling between the auxiliary hidden neurons, the hidden variables can be traced out. The RBM variational wave function thus reads


The evolution of the wave function can be obtained through a simple Markov process that is defined by (x,w),which is named as a walker. This Markov process is described as follows:
(i) Transform a configurationxintox′with probabilitypx′,x.
(ii)Update the weight withw′=wbx.




Fig. 2. The principal component of the variational wave function of the frustrated J1–J2 Heisenberg model on a 6×6 square lattice with J2 =1.0. The black squares denote the results of the variational wave function corresponding to different configurations,and there are 2×104 black squares in the figure. The principal component represent by the red line.
The PCA is a type of variable reduction method which is adopted to analyze datasets described by several intercorrelated variables. This method can effectively extract important information from a dataset,then represent it as a set of new orthogonal variables defined as principal components. In this work, we utilize the PCA method to extract the principal component of the guiding wave functions so as to reduce the wave functions from the complex space to the real space.
As shown in Fig. 2, we consider the frustratedJ1–J2Heisenberg model on a 6×6 square lattice withJ2=1.0.Sampling a large number of configurations, the corresponding results of the variational representation are shown by the black squares in the complex coordinate system. And the principal component is represent by the red line. The projections of the values of the variational wave function on the principal component axis are the new real wave functions.
3. Results
With its implementation, we first benchmark the GFMC+RBM method by exact diagonalization method on a 4×4 square lattice.
Figure 3 shows the dependence of the ground-state energy on the total imaginary-timeβtotalon a 4×4 square lattice.With the increase ofβtotal,the ground-state energies calculated by the GFMC decrease gradually from the one given by the RBM until they reach the exact value. For three different single Markov step lengthβ,we all get the same result.
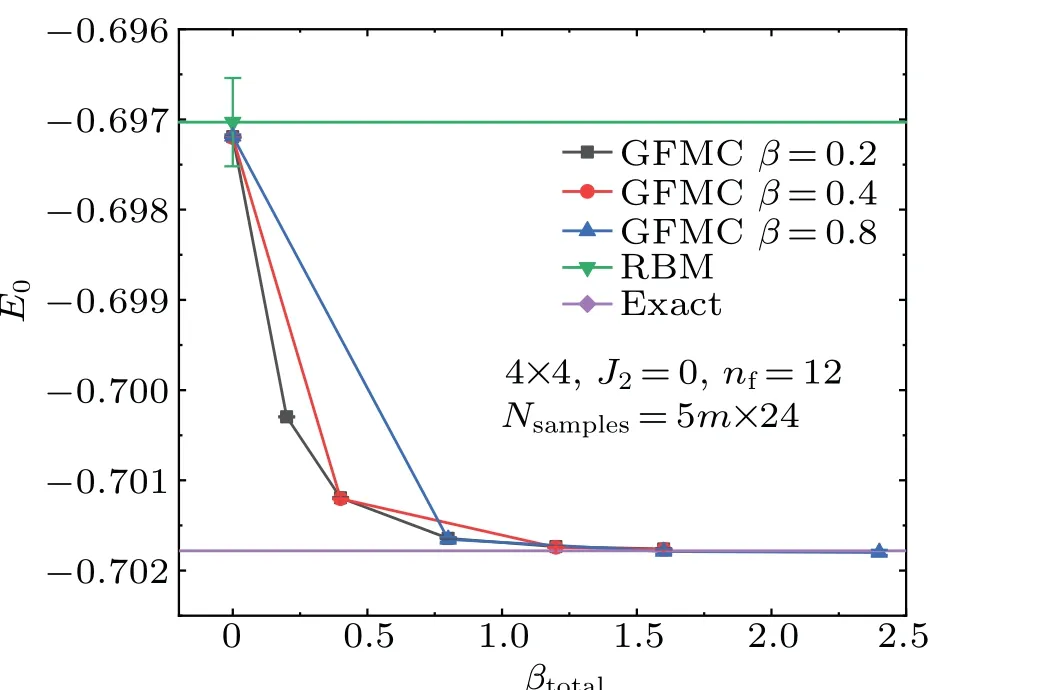
Fig. 3. The ground-state energy as a function of the imaginary-time βtotal on a 4×4 square lattice with three different β. βtotal is the total evolution time,and β represents the evolution time for a single Markov step. nf is the ratio of the number of hidden units to visible units for the architecture of the RBM guiding wave function.
Next, we employ the GFMC+RBM method to study the frustratedJ1–J2Heisenberg model on a 6×6 square lattice.The obtained relative errors and spin structure factors are shown in Figs.4 and 5 respectively. Here the relative error is defined as|(E −Eexact)/Eexact|,whereEexactis the exact value of the ground state energy. The spin structure factor is defined by Eq.(2).
As shown in Fig. 4, in comparison with the RBM, the GFMC+RBM method substantially reduces the relative errors of the ground state energies. One notices that the relative errors decrease significantly away from the transition region.The GFMC+RBM method performs in the phase transition region not as well as it does in the non-phase transition regions.It is well known that the characteristics of the phase transition region are still controversial due to the competing orders in this region. Actually, the variational results of the RBM get larger errors in this region,the RBM as a guiding wave function is thus not sufficiently precise for the GFMC,then leading to larger errors for the GFMC as well in the phase transition region. This suggests to find a neural network with stronger expressibility instead of the RBM serving as a better guiding wave function for the GFMC.
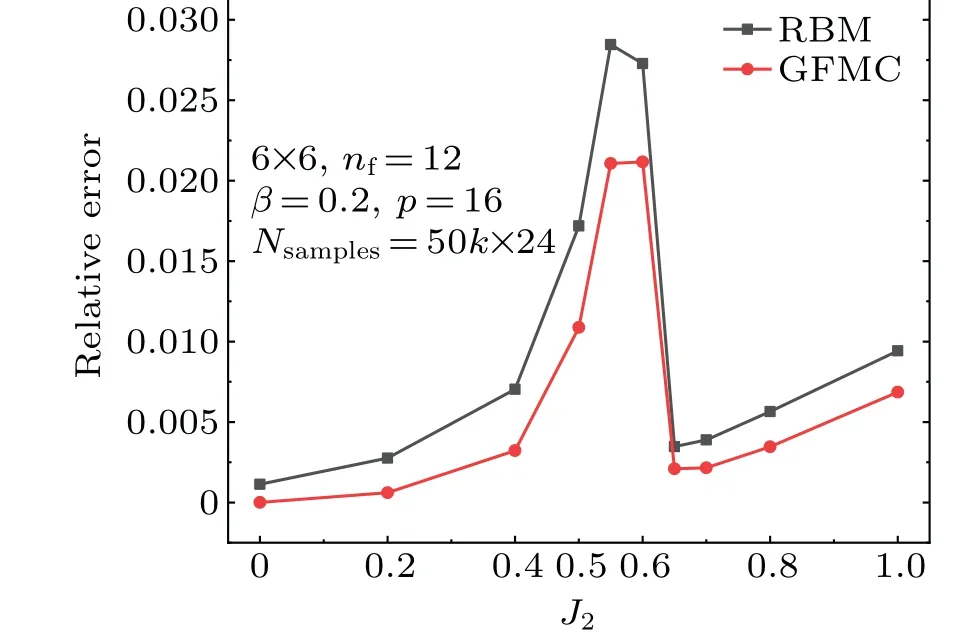
Fig.4. The relative errors of the RBM and GFMC+RBM method results for the frustrated J1–J2 Heisenberg model on a 6×6 square lattice. The vertical axis represents the relative errors |(E −Eexact)/Eexact|, the exact results are taken from the Ref.[31],and the number of filters of RBM is nf=12.
Figure 5 shows the phase transition diagram on a 6×6 square lattice with differentJ2values. The vertical axis represents the spin structure factor. Fork=(π,π), the calculation results are shown as the black dots, and the spin structure factor can be used to indicate whether or not there is a Neel phase transition. A Neel AFM order exists in the system whenJ2<0.45, while it gradually disappears forJ2>0.5.The range of 0.45 Fig.5. The spin structure factors of frustrated J1–J2 Heisenberg model on a 6×6 square lattice. The error bars represent the statistical errors of the GFMC method. Figure 6 shows the spin structure factors calculated on a 10×10 square lattice. The detailed calculation results of 6×6 and 10×10 square lattice are listed in Tables 1 and 2,respectively. Fig.6. Spin structure factors of frustrated J1–J2 Heisenberg model on a 10×10 square lattice. The error bars represent the statistical errors of the GFMC method. Table 1. Comparison between the RBM and RBM+GFMC method relative errors of ground state energies. The last row is the ratio between them. The exact energies on a 6×6 square lattice are taken from Ref.[31]. Table 2. Comparison of ground-state energies between the RBM and GFMC+RBM method on a 10×10 square lattice. In this paper, we implemented the combination of the GFMC method and the RBM to study the frustratedJ1–J2model on a square lattice. Taking the variational result of the RBM as a guiding wave function for the GFMC, we calculated the ground state energies and spin structure factors of the model with differentJ2on a 6×6 square lattice,and then compared the results between the GFMC+RBM method and the pure RBM method. The GFMC+RBM method improves the accuracy of the ground state energies. And the spin structure factors given by the GFMC+RBM method are also better than those of the pure RBM method.Similar conclusion can be obtained in the study for a 10×10 square lattice. Overall,the GFMC+RBM method well outperforms the RBM. It is very instructive to combine the RBM and GFMC method to study quantum systems with sign problem. This encourages to replace the RBM wave function with other neural networks with stronger expressibility like CNN on more challenging models in the future. Appendix A:The comprehensive comparison between the RBM and random initial states We carried out the calculations and made a comprehensive comparison between the random initial states and the RBM. We show that for the GFMC the RBM as a guiding wave function well outperforms the random initial states as guiding wave functions. We prepared the random initial states by setting up the RBM with randomly generated network parameters so that the RBM gives random wave functions,whose nodal surfaces are hence also random and whose energies are around zero and far above the true ground state energies. As the following tables show, for both 4×4 and 6×6 square lattices and for bothJ2=0 and 0.55,when the random states are used respectively as a guiding wave function,the GFMC can only slightly reduce the energies and the minimized energies are still far above the exact ground state energies. As a contrast, when the variationally optimized RBM states used respectively as a guiding wave function, the minimized energies are close to the exact ones,showing that the variationally optimized RBM states possess a meaningful nodal surface and well outperform the random initial states. Table A1. Ground state energies for the frustrated J1–J2 model on the 4×4 square lattice,nf=2,βtotal=6.4,Nsamples=5m×24. Table A2. Ground state energies for the frustrated J1–J2 model on the 6×6 square lattice,nf=12,βtotal=6.4,Nsamples=50k×24. Acknowledgements Project supported by the National Natural Science Foundation of China(Grant Nos.11934020 and 11874421)and the Natural Science Foundation of Beijing(Grant No.Z180013).Computational resources were provided by National Supercomputer Center in Guangzhou with Tianhe-2 Supercomputer and Physical Laboratory of High Performance Computing in RUC.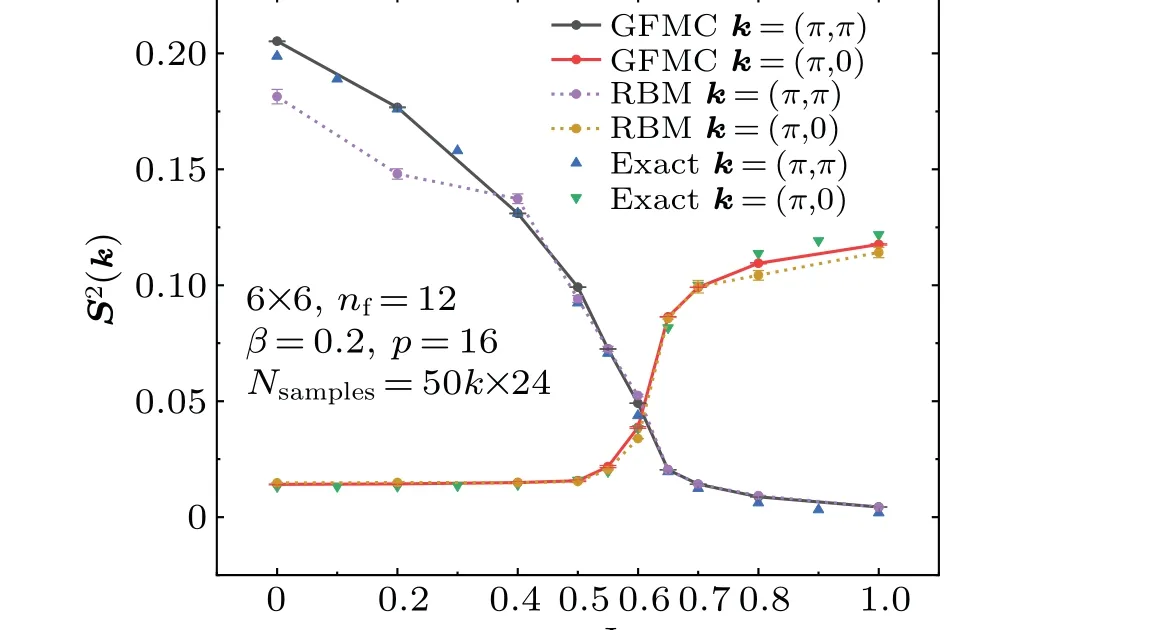



4. Summary


- Chinese Physics B的其它文章
- Direct measurement of two-qubit phononic entangled states via optomechanical interactions
- Inertial focusing and rotating characteristics of elliptical and rectangular particle pairs in channel flow
- Achieving ultracold Bose–Fermi mixture of 87Rb and 40K with dual dark magnetic-optical-trap
- New experimental measurement of natSe(n,γ)cross section between 1 eV to 1 keV at the CSNS Back-n facility
- Oscillation properties of matter–wave bright solitons in harmonic potentials
- Synchronously scrambled diffuse image encryption method based on a new cosine chaotic map

