Effects of oxygen concentration and irradiation defects on the oxidation corrosion of body-centered-cubic iron surfaces: A first-principles study

Zhiqiang Ye(叶志强) Yawei Lei(雷亚威) Jingdan Zhang(张静丹) Yange Zhang(张艳革)Xiangyan Li(李祥艳) Yichun Xu(许依春) Xuebang Wu(吴学邦) C.S.Liu(刘长松)Ting Hao(郝汀) and Zhiguang Wang(王志光)

1Key Laboratory of Materials Physics,Institute of Solid State Physics,HFIPS,Chinese Academy of Sciences,Hefei 230031,China

2University of Science and Technology of China,Hefei 230026,China

3School of Mechanical Engineering,Suzhou University of Science and Technology,Suzhou 215009,China

4Institute of Modern physics,Chinese Academy of Sciences,Lanzhou 730000,China

Keywords: oxidation corrosion, oxygen concentration, irradiation defects, bcc-Fe surfaces, first-principles study

1. Introduction

Oxidation corrosion is an important problem for steels operating in oxygen-contained environments. It becomes severe when the steels as structural materials are in contact with coolant with high oxygen concentration and irradiation environments in nuclear reactors. The severe corrosion can lead to rapid growth in the oxidation layer on the surface of structural materials. The increased oxidation layer not only significantly reduces the heat conduction of structural materials but also increases the lockage risk of the coolant loop due to the spalling of oxidation. Therefore,it is necessary to understand how the oxidation layer is formed and which factors affect the growth of the oxidation layer on the iron(Fe)-based structural materials.

The oxidation layer on the Fe-based structural materials is usually composed of the outer oxide layer(Fe3O4)and the inner oxide layer ((Fe, Cr)3O4),[1,2]as in contact with the oxygen-contained environment from experimental research.An available space model was proposed to explain the formation mechanism of the oxide layer on the surface of Fe-based structural materials in oxygen-contained environments.[1,2]In this model,Fe atoms go out and combine with oxygen atoms outside forming the outer oxidation layer,Fe3O4,meanwhile,leaving enough space for oxygen atoms coming into the bulk-forming inner oxidation layer (Fe, Cr)3O4. The growth rate of the oxidation layer depends on the migration rate of cations in the oxidation layer and the oxygen concentration at the interface,[3]which depends on temperature,[4–6]oxygen concentration[4,5,7,8]and irradiation dose.[9,10]Yeliseyeva[4]revealed that the corrosion rates for T91 and AISI 316L steels increase with increasing temperature. Gorynin[7]found that the concentration of oxygen in liquid metals (lead or leadbismuth eutectic, LBE) determines the corrosion of steels.High oxygen concentration(>10−6%)leads to oxidation corrosion, which is accelerated rapidly with increasing oxygen concentration, although low oxygen concentration (10−10%–10−8%) results in dissolution corrosion. Frazer[9]found that passive oxide structures grow on the ferritic/martensitic steel HT9 in contact with oxygen-contained LBE while being irradiated, even the oxidation layer is greatly increased by the irradiation and spall off the surface. Meanwhile, irradiation not only affects the thickness of the oxidation layer but also changes the structure of the oxidation layer.[10]However, the micro-pictures of oxygen atoms adsorbing on the surfaces and migrating into the bulk in high oxygen concentration and irradiation environments cannot be observed by these experiments at the initial oxidation stage.

Some theoretical simulations have been investigated to explore the formation of oxidation,[11–17]such as adsorption properties of oxygen on the body-centered-cubic (bcc)-Fe surfaces and the solution and diffusion of oxygen in bcc-Fe bulk. Based on density functional theory, people found that oxygen molecules (O2) dissociate firstly, then energetically adsorb at the hollow position on the Fe(100) and longbridge position on Fe(110) surface. The adsorption depends on the coverage of oxygen atoms and alloying atoms on the surfaces.[14,18,19]In the bulk,oxygen atoms prefer to solute at octahedral interstitial sites (OCT) of the Fe lattice[15,16]and diffuse quickly to the next OCT site with the energy barrier of 0.54 eV.[17]However, they are easily trapped by vacancy defects and grain boundaries, which also slow down the diffusion of oxygen.[20–22]Besides,the effects of alloying atoms on the solution and diffusion of oxygen are also explored in Fe-based alloys.[21,23]The bond order analysis potential of the Fe–O system has been proposed to reproduce the fundamental properties of the Wustite and the energetics of oxygen atoms inα-iron.[24]However,little literature has clarified the micropicture of the oxidation process at the initial stage: how oxygen atoms migrate and dissolve in the near-surface region after adsorption on the surfaces,and how the oxygen concentration and irradiation affect the solution and migration of oxygen atoms?

In this paper,we aim to acquire the mechanism of oxidation corrosion by focusing on the adsorption/solution properties of oxygen atoms on/under the Fe(100) and Fe(110) surfaces as well as their dependences on oxygen coverage and irradiation defects, and the migration properties of oxygen atoms. Firstly, the basic properties of clean surfaces, such as their surface energies, electronic work function and magnetic moments are investigated by the first-principles calculations to make sure the reasonable models and parameters are used in this work. Then,the adsorption properties of oxygen atoms on Fe surfaces are explored by the adsorption energies of O atoms at the most stable positions on Fe(100) and Fe(110) surfaces with different coverage. The insight into the local structure is explored by the charge density difference and the electronic local density of states at the atomic level. In addition, the influence of oxygen concentration and vacancy defects on the solution and migration of oxygen atoms are studied to derive the micro-picture of oxidation corrosion of Fe surfaces. Finally,the effects of oxygen concentration and vacancy on the oxidation corrosion of Fe surfaces are further discussed in contact with oxygen-contained environment and irradiation.

2. Model and method

2.1. Computational details

All calculations presented here have been performed using the density functional theory (DFT) implemented in the Viennaab-initiosimulation package (VASP).[25,26]The generalized gradient approximation (GGA) with the exchange–correlation energy of Perdew–Burke–Ernzerhof (PBE) is adopted.[27]The interaction between ions and electrons is represented by the projector augmented wave (PAW) potentials method with the 3d74s1electrons treated as valence electrons for Fe atoms.[28–30]As a result of the convergence tests, the cutoff energy of 500 eV is used to expand the electronic wave functions,and the first order Methfessel–Paxton method with the Fermi surface smearing of 0.20 eV is adopted to accelerate the convergence. The spin polarization of Fe is performed because of its magnetic properties. With thek-point mesh of 12×12×12, the lattice constant of the body-centered-cubic iron (bcc-Fe) is optimized to be 2.831 ˚A, which is consistent with experimental data and other DFT calculations.[31–33]

The two clean surfaces of bcc-Fe with low index (100)and (110) are modeled by the optimized unit lattice with a 15 ˚A vacuum layer between the periodic slabs in [001] and[110]directions,respectively. As shown in Fig.1,the Fe(100)and Fe(110)surfaces consist of a 3×3 unit cell with 9 atomic layers. Ak-point mesh of 5×5×1 is generated automatically using the Monkhorst–Pack method.[34]The bottom three layers in dashed squares are fixed as bulk in Figs. 1(a) and 1(b),and the rest layers are fully relaxed to mimic Fe(100)and Fe(110)surfaces until the force convergence of 0.01 eV/˚A.

The O atoms adsorbed surfaces are constructed based on the optimized clean surfaces with oxygen atoms at different high-symmetric sites to determine the lowest energy configuration. As labeled in Fig. 1, hollow (H), bridge (B) and top(T)positions are considered on the Fe(100)surface,and longbridge (LB), short-bridge (SB) and top (T) sites are considered on the Fe(110)surface. The configuration with the lowest energy is chosen as the most stable one and then utilized to analyze the adsorption/solution properties of oxygen atoms on/under the two surfaces. For investigating the coverage(θ)dependence of the adsorption/solution properties, the stable configurations are initiated by adding a different number of adatoms on the surfaces, correspondingθfrom 0 to 1. For example, one adatom and nine adatoms on the 3×3 unit cell(surface atoms as shown in Fig. 1) correspond to the monolayer coverage of 1/9 and 1, respectively. Thek-points and cutoff energy are tested until the deviation of total energies for the systems is within 0.05 eV.

Fig. 1. The side view of Fe(100) surface (a), and Fe(110) surface (b),and the overview of Fe(100)(c)and Fe(110)(d), respectively. Orange dashed squares labeled B represent relaxed surface, while labeled B′represent bottom surface with fixed layers,and the middle cyan region labeled A is the bulk-like region. The blue balls are surface Fe atoms,and the gray balls are Fe atoms at sub-layers. Yellow dashed circles represent the high-symmetric positions for adatoms on a different surface, such as hollow (H), bridge (B) and top (T) on the (100) surface,and long-bridge (LB) and short-bride (SB) on the (110) surface. The numbers 1,2,3,...,8 represent other H positions on the(100)surface,LB on the(110)surface.

2.2. Analysis technology

The surface energy of the model with different atomic layers is firstly investigated to avoid the periodic effect of the surface for assuring the reliability of the model. The surface energyEsis defined as[35–39]

wheredis an interplanar spacing in the bulk. The positive sign∆ijmeans expansion,while a negative value means contraction.

Oxygen atoms have to be adsorbed on the Fe surfaces and penetrate the bulk, as oxidation happens. To characterize the capability of oxygen atoms adsorbing/solving on/under the surfaces, we define the adsorption energies/solution energies of oxygen atoms on/under the surfaces as the following equation:[41–49]

3. Results and discussion

3.1. Basic properties of clean Fe(100)and(110)surfaces

The surface energies of the models with different layers and unit cells are firstly explored and shown in Table 1 to check the reliability of models. The surface energy is almost constant as the model expands in surface and layer,indicating that a surface model of 3×3 supercell and 9 atomic layers is sufficient and economic in the study. According to Eq.(1),the surface energies calculated for Fe(100) and Fe(110) surfaces are 2.49 J/m2and 2.41 J/m2,respectively. Those results are in very good agreement with experimental data and other theoretical results,such as 2.48 J/m2[39,51]of Fe(100),2.43 J/m2[38,51]of Fe(110). The work function defined as the difference between the electrostatic potential energy in vacuum zone and the Fermi level are calculated to be 3.86 eV for Fe(100) surface and 4.75 eV for Fe(110) surface, respectively, which show a good agreement with previous results (3.90 eV[12,51]for Fe(100), 4.77 eV[12,38,51,52]for Fe(110)). The magnetic moments of Fe atoms on Fe(100) and Fe(110) surfaces are 2.96µBand 2.60µB, which are also consistent with our previous results(2.95µB[18,39,42,51]for Fe(100),2.59µB[12,38,51]for Fe(110)). These results indicate that our models are reasonable and calculations are credible.

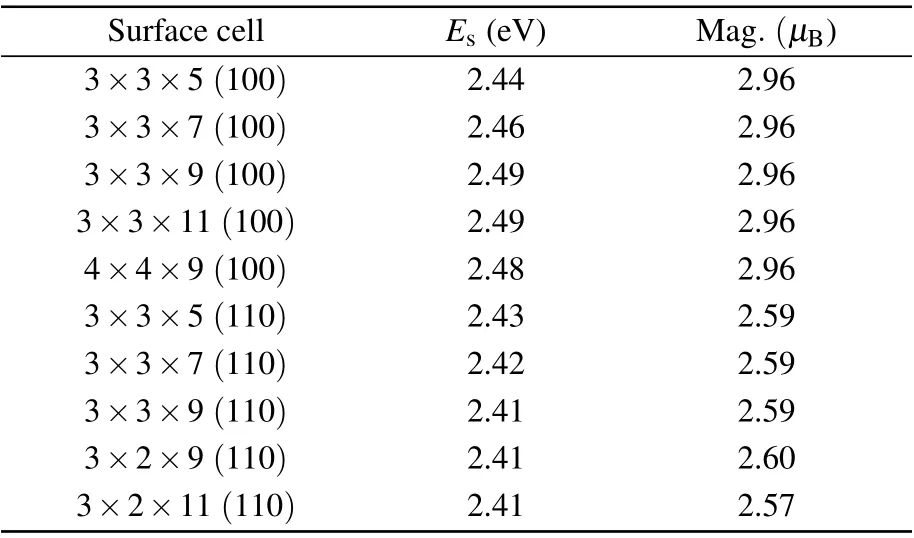
Table 1. Convergence of surface energy Es and magnetic moments of Fe atoms for Fe(100)and Fe(110)surface.

Figure 2 shows the relaxation of the interplanar distance of Fe(100)and Fe(110)surfaces with and without fixed atoms on the bottom three layers according to Eq. (2). In the models of Fe(100)and(110)surfaces,the interplanar distancesd45andd56in zone-A tend to be 0,which indicates that zone-A is the bulk-like region in the model. Thed12,d23andd34in the near up-surface region(zone-B)show similar behavior for the surfaces with and without fixed atoms on the bottom three layers,althoughd67,d78andd89for the near down-surfaces show the visible difference. These results indicate that the surface models with fixed bottom three layers can be economically used in the following studies to investigate the interactions between oxygen atoms and surfaces. On the Fe(100)surface,the interplanar distanced12decrease by 1.73%,whiled23andd34increase by 3.46%and 0.78%respectively,compared with the bulk. On the Fe(110) surface,d12andd23expand by 0.16%and 0.83%, respectively. They are in good agreement with other calculations and experimental results.[12,38,51,53]

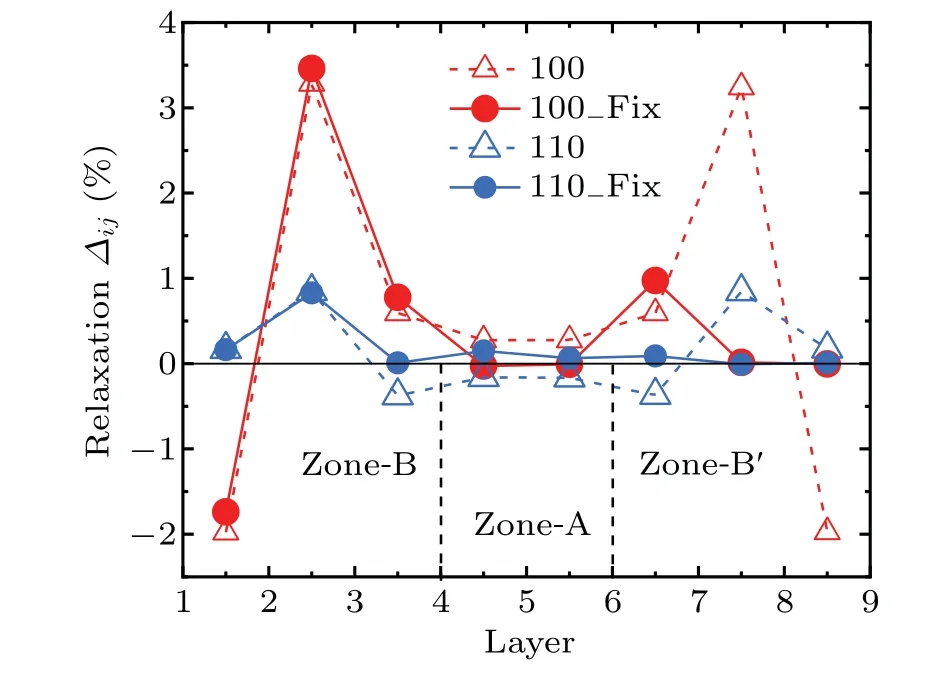
Fig.2. The relaxation of the interplanar distance for the clean Fe(100)and(110) surfaces. The red and blue solid circles show the relaxation of the interplanar distance for the surfaces with fixed bottom three layers, while the red and blue hollow triangles indicate the relaxation of the interplanar distance for the fully relaxed surfaces. The black solid lines show the relaxation of the layer spacing relative to the bulk. Zone-A, zone-B and zone-B′ represent bulk-like region and surface regions.Respectively,as shown in Figs.1(a)and 1(b).

3.2. Adsorption properties of oxygen atoms on Fe surfaces

Table 2. Adsorption energy of one O atom (E1Oads in eV) at different high-symmetric sites on the clean Fe(100)and Fe(110)surfaces.

The surface dependence of the adsorption of O atoms on Fe surfaces is further investigated by the charge density difference at the interface between O atoms and Fe surfaces according to previous investigations.[13,54]The charge density difference(∆ρ),is defined by the total charge of the slab with an adatom subtracted by the total charge of the slab and the adatom. Negative ∆ρrepresents that local electrons are depleted, and positive ∆ρmeans that local electrons are accumulated. Figure 3 shows the ∆ρdistributions around O atoms on the Fe(100) and Fe(110) surfaces both in the side and top views,respectively. It is noticed that there are substantial rearrangements of electrons around the adsorbed O atoms and Fe atoms on the two surfaces. The ∆ρvalues around O atoms are positive, indicating the electrons around Fe atoms are transferred to the O atoms on the surface. On the Fe(100)surface,the adsorbed O atoms accumulate more electrons than those on the Fe(110)surface. The charge depletion is also checked based on the Bader’s theory.[55,56]Relative to the 6 valence electrons for O atoms (2s2p4), they accumulate 1.34eand 1.16ewithin their Bader volume on the Fe(100) and Fe(110)surfaces,respectively. The transferred charges from Fe atoms to O atoms on the surface are greater than 0.83eas in bulk bcc-Fe. These results indicate that the interaction between O and Fe atoms on the Fe(100) surface is stronger than on the Fe(110) surface, and the ionic character of Fe–O interaction on the surfaces is stronger than that in the bulk. The ionic character is further investigated by the density of state analysis of O atoms and their adjacent Fe atoms on the two surfaces as shown in Figs.3(c)and 3(f). The electronic density of p-state for O atoms exhibits sharp peaks with narrow energy range,indicating that localized character of the electronic density of O-2p orbitals, and O-2p and Fe-3d orbitals show weak hybridization. Meanwhile,the charge transfer of Fe atoms under the Fe(100)is affected by the adsorbed O atoms more severely than that below the Fe(110)surface.

Fig.3. Charge density difference of an O atom at H position on Fe(100)in top view(a)and side view(b),and at LB position on Fe(110)in top view(d),and side view(e)and the electronic local density of states(LDOS)of an O atom at H position on Fe(100)(c)and at LB position on Fe(110)(f). Yellow and blue colors refer to electron accumulation and depletion zones,respectively. Brown and red balls are labeled as Fe and O atoms,respectively. The iso-surface of charge density is 0.008 e/Bohr3. Positive/negative values of LDOS represent majority/minority spin states,respectively. The vertical dash line marks Fermi level.

Table 3. The lowest adsorption energies of the last O atom(EaladsstO)and the n O atoms with the most stable confgiurations(EandOs)on the Fe(100)and Fe(110)surfaces with different coverage,and the number of O atoms in the first nearest neighbors(1NN)and second nearest neighbors(2NN)on the two surfaces with different.

Fig. 4. (a)Adsorption energies () ofOatoms and(b) binding energies()of Oatoms on the (100) and (110)surfaces with differentcoverage.The greensolid circles and opensquares in(a) indicate the adsorptionenergies()of the last adsorbed O,corresponding to the right scale.

Fig.5.(a)The change in the average positions of Fe atoms and the average distances of O atoms to the first adsorbed O atom on the surfaces as function of the oxygen coverage(θ). (b)The nearest distance between O atoms as function of θ.

Fig. 6. Two-dimensional side view of charge density difference around the 7th O atom adsorbed on the Fe (100) surface by cutting off the model along [100] (a) and [110] (b), and around the 10th O adsorbed on the Fe(100) surface by cutting off the model along [100] (c) and[010] (d). Three-dimensional top view of charge density difference around the 7th O atom (e) and 10th O atom (f) on the Fe(100) surface.In (a)–(d), red stars and black dots represent the adsorbed O atoms and Fe atoms on/in the surface/near-surface region. O1, O5, O6, O7, ...are O atoms with the adsorption sequence and the Fe1, Fe2, Fe3, ... indicate Fe atoms at different layer. The accumulation or depletion of charges are demonstrated by the color scale in(a)–(d). Yellow and blue colors in(e)and(f)refer to electron accumulation and depletion zones,respectively. Brown and red balls are labeled as Fe and O atoms,respectively. The iso-surface of charge density is 0.008 e/Bohr3.

3.3. The effects of oxygen coverage on oxidation corrosion

Fig.7. Solution e(b),respectively.The black horizontal dash line indicates the solution energy(−1.20 eV[15,16,22])of an interstitial O atom at octahedron position in bulk.

Fig. 8. (a) The energy barrier of one O atom migrating from one “H” to its first neighbor “H” and second neighbor “H” on Fe(100) (a) and from one“LB”to its first neighbor“LB”and second neighbor“LB”on Fe(110),respectively. (b)The energy diagram of O atoms migrating from the Fe(110)surface with oxygen coverage of 1/4 to the bulk-like region.

The dynamic properties of O atoms on the Fe surfaces are investigated through the energy barriers of O atoms diffusing on the surfaces. Figure 8(a) shows the energy barriers of O atoms migrating on Fe(100)and Fe(110)surfaces in different paths, respectively. An O atom has to overcome an energy barrier of 0.65 eV and 1.48 eV for migrating in the paths of H–H1NNand H–H2NNon Fe(100) surface, respectively. Meanwhile,it overcomes 0.45 eV and 1.56 eV for migrating in paths of LB–LB1NNand LB–LB2NNon Fe(110)surface,respectively. This indicates that O atoms prefer to move from one most stable to their first neighbor’s most stable positions. Meanwhile, the energy barrier of O atoms diffusing on the Fe(110) surface is lower than that on Fe(100) surface,indicating that the diffusion of O atoms on the Fe(110)surface is easier than that on Fe(100)surface.

Besides, the dynamic behavior of O atoms from surface to bulk is further explored and compared with that on the surfaces. Here,the Fe(110)with oxygen coverage of 1/4 is taken as an example, since O atoms can stay at the near-surface region. As shown in Fig.8(b),one of O atom needs to overcome 2.74 eV to migrate into the near-surface region,while 0.57 eV to diffusion in bulk region,showing good agreement with previous results(0.53 eV[16,20]). The energy barriers of O atoms migrating from the surface to the bulk region are significantly higher than those on the surfaces, therefore, O atoms prefer to diffuse on the surfaces compared to the bulk region. Therefore,when bcc-Fe-based structure materials are in contact with the oxygen contained environment,O atoms would adsorb and then diffuse on the surfaces with low oxygen coverage,and finally go through the near-surface region with the repulsion of O atoms adsorbed on the surfaces with high coverage.

3.4. The effects of irradiation defects on oxidation corrosion

Then, the solution energies of O atoms near vacancies in near-surface and bulk regions are calculated according to Eq. (3) for investigating the effects of vacancies on the solution of O atoms. As shown in Fig. 10(a), the solution energies of O atoms near vacancies increase with the increasing depth of oxygen atoms from the surface. The increasing trend is the same as that in the surface model without any vacancies. However,the adsorption energies of O atoms are almost not changed as O atoms are adsorbed on the surfaces,but the solution energies of O atoms are much reduced by vacancies in near-surface and bulk regions. This leads to an obvious increase in the segregation energies of O atoms due to the vacancies (e.g., from−2.76 eV to−1.28 eV). Therefore, O atoms can be easily bound by vacancies, which reversely affect the solution of O atoms in near-surface and bulk-region.

Fig. 9. Vacancy formation energies (Evf) are functions of the distance from the surface.

Fig. 10. (a) Solution energies of an O atom with or without vacancy at different distances to the surfaces with different coverage. The black horizontal dash lines indicate the solution energies of an O atom located on OCT in bulk with and without a vacancy nearby. EOseg indicate the segregation energies of O atoms on the Fe(100)and(110)surfaces with and without vacancies. (b) Binding energies (Ev+Obin ) of the vacancy with oxygen as functions of their distance to the(100)and(110)surfaces. The green solid diamonds and open triangles in (b) indicate O atoms are the second nearest neighbors(2NN)to the vacancies. The black horizontal dash line indicates the binding energy of an O atom and vacancy in bulk.

The effects of vacancies on the dynamic behavior of O atoms are studied by the energy barriers of O atoms around a vacancy diffusing from the surface towards the near-surface region. The Fe(110) with coverages of 1/4 and 1/2 is again taken as examples for comparing with the diffusion of an O atom in a defect-free surface system shown in Fig. 8. As shown in Fig. 11(a), an O atom diffuses from a first nearest neighbor of the vacancy on the surfaces to another first nearest neighbor position in the near-surface region. The energy barrier of an O atom around a vacancy on the Fe(110)surface with coverage of 1/4 is 1.87 eV in Fig.11(b), which is much less than 2.74 eV in the defect-free system. The energy barrier of an O atom around a vacancy on the Fe(110)is reduced to be 1.18 eV,as the coverage of O atoms increases from 1/4 to 1/2. These results indicate that both vacancies and oxygen concentration could accelerate the diffusion of O atoms into the near-surface region,and further lead to quick oxidation in experiments.

Fig.11. (a)The migration path diagram of O atoms with and without(w/o)a vacancy migrating from the Fe(110)surface to the subsurface when the coverage increases from 1/4 to 1/2,and(b)the corresponding migration energy diagram.

3.5. Discussion

As we know, oxidation of bcc-Fe-based steels would be accelerated under either high oxygen concentration or irradiation. The picture of the oxidation of bcc-Fe surfaces at the initial stage has been sketched in Fig. 12 based on the above studies on the adsorption/solution and migration properties of O atoms on/under the surfaces with different coverage of O atoms and vacancies. In a low oxygen concentration environment,O atoms adsorb on the surfaces with low coverage,and probably diffuse on the surfaces. With irradiation-induced vacancies, they would migrate into the bulk region. In a high oxygen concentration environment,O atoms adsorb on Fe surfaces with high coverage,and then further diffuse into the bulk region with the repulsion from the continuously approaching O atoms from the environment. Meanwhile, Fe atoms on the surfaces are pulled out,leaving more space for O atoms.

Fig. 12. The oxidation mechanism of Fe surfaces with low oxygen coverage (a) and high oxygen coverage (b). 1 and 3 indicate the adsorbing of O atoms on the surfaces and the diffusion of O atoms from the surface into bulk.2 indicates the diffusing processes of O atoms on the surfaces with low oxygen coverage and repulsing processes between O atoms on the surfaces with high oxygen coverage. The grey and red balls indicate the Fe atoms in lattice and O atoms, while blue balls and blue dashed circles represent Fe atoms pulled out and vacancies,respectively.

To intuitively describe the effects of oxygen concentration and irradiation on oxidation,we try to estimate an equilibrium oxygen density in near-surface and bulk regions. Ignoring the interactions between O atoms at the same atomic layers in the near-surface and bulk region,the relationship of concentration of oxygen on surfaces and in bulk can be described by the McLean’s equation[58–60]

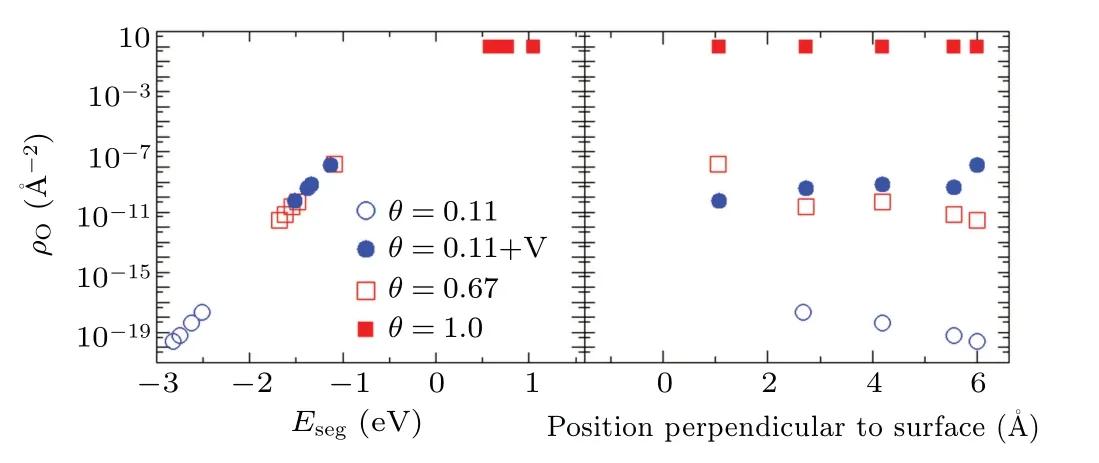
Fig.13. The concentrations of oxygen as function of the energy of an oxygen segregating from near surface or bulk region to the surface(a),and the position of an oxygen perpendicular to the Fe(100)surface(b).The blue open circles,red open squares and red solid squares represent the densities of oxygen at different positions relative to the surface with oxygen coverage of 0.11,0.67 and 1.0,respectively. The blue solid circles are the densities of oxygen in near-surface and bulk region with low coverage of oxygen and vacancies.

In addition, the effect of irradiation on oxidation is explored by the density of O atoms at the atomic layers with vacancies nearby in the near-surface and bulk region. Besides the effects of O atoms on the surfaces, other interactions between O atoms or vacancies nearby are not considered in the model. With the same low coverage of O atoms on the surface(1/9),vacancies decrease the solution energies of O atoms in the near-surface and bulk region as shown in Fig. 10(a),and obviously improve the segregation energies. Therefore,the densities of O atoms in the near-surface and bulk region would be significantly promoted in several orders of magnitude by the irradiated vacancies. Meanwhile,the density of O atoms under the surfaces does not depend on the depth of O atoms from the surface. This is due to the very simple hypothesis here, which vacancies distribute the same at the surface and bulk,and interactions between vacancies are ignored. The effects of irradiation on the distribution of O atoms in the nearsurface region will be further studied in the next work at a large scale with these parameters.

4. Conclusions

Based on first-principles calculations, the oxidation mechanism of bcc-Fe surfaces at the initial stage is explored by systematically investigating the adsorption/solution properties and diffusion behavior of oxygen atoms on/under iron surfaces. The adsorption energies show that surfaces have a strong attraction to oxygen atoms, and the attraction strength depends on the local structure and oxygen coverage. The solution energies of O atoms are closely related to the coverage of oxygen atoms adsorbed on the surfaces and irradiated vacancies in near-surface and bulk regions. With the increase in oxygen coverage and vacancies, oxygen atoms gradually dissolve in the near-surface region. Dynamic results indicate that the oxygen atoms prefer to diffuse on the surfaces than into the near-surface region,and the diffusion process is promoted by the coverage of oxygen atoms on the surface and vacancies.Moreover,the effects of oxygen concentration and irradiation on oxidation are roughly estimated by the McLean’s model with a simple hypothesis. This paper reveals the microscopic mechanism of oxidation corrosion of O atoms on Fe surfaces,provides parameters for the further investigation of oxidation corrosion under nuclear energy irradiation environment.

Acknowledgements

Project supported by the National Key Research and Development Program of China (Grant Nos. 2017YFE0302400 and 2017YFA0402803),the National Nature Science Foundation of China (Grant Nos. 11735015, 52071314, 51871207,U1832206,12075274,U1967211,52171084),and Hefei Advanced Computing Center.